重載鐵路軌道高低不平順預測研究
包文艷,王福田,李仕毅,張 寧
(1.中國神華神朔鐵路分公司,陜西榆林 719316;2.北京交通大學軌道交通控制與安全國家重點實驗室,北京 100044)
神朔鐵路自陜西大柳塔鎮至山西朔州市,正線全長265.75 km,是國家Ⅰ級電氣化重載運煤專線鐵路[1],作為國內重要的運煤干線,運輸任務繁重,具有貨運量大、車流量大、裝車站多、裝車量大、貨物單一和整列裝運等特點[2]。軌道不平順嚴重威脅鐵路行車安全、設備的使用壽命等[3]。軌道高低不平順作為度量軌道不平順的指標之一,不僅是評價軌道質量最具代表性的指標[4],而且是編制搗固作業計劃的主要參考依據[5-7],具有重要研究意義。
軌道高低不平順是垂直于軌道方向的不平順,描述鋼軌頂面沿延長方向在垂向的凹凸不平[8],主要是由鋼軌表面不平整和軌枕、路基、道床等彈性形變不均勻造成[9]。根據左、右鋼軌的變化差異,又分為左高低和右高低不平順。軌道高低不平順會使輪軌間產生強烈的沖擊,引起較大的相互作用力,導致軌道結構和機車部件損壞,也會使輪載發生急劇的增減變化,易導致機車脫軌,嚴重影響行車安全[8]。
國內外有不少專家對軌道高低不平順的預測等開展過研究。Famurew等[7]建立了軌道高低不平順的指數預測模型。Caetano等[10]通過考慮搗固次數對軌道高低不平順的影響,建立了高低不平順的線性預測模型。Caetano等[6]結合線性模型和不確定性,建立了軌道高低不平順的線性不確定性預測模型。許玉德等[11]利用特性矩陣,預測軌道高低不平順的變化。周宇等[12]采用多元回歸分析,建立了廣深線軌道高低不平順的非線性預測模型。高建敏[13]通過利用系統狀態轉移概率矩陣法,建立高低不平順25 m區間最大值狀態轉移概率矩陣,對高低不平順區間最大值的發展狀況進行預測。何永春等[14]對滬寧線的軌道高低不平順進行了預測分析。
上述研究缺乏對軌道高低不平順動態隨機性和異質性二者的全面考慮。動態隨機性是指軌道高低不平順由于軌道因素、荷載因素、自然因素等諸多因素共同作用導致的動態隨機發展特性,異質性是指軌道高低不平順在不同里程位置上變化規律不同。而灰色區間預測建模方法可以很好地應用于在多種復雜因素作用下具有不確定性、動態發展等特性的振蕩序列的變化規律的分析研究[15]。本文基于灰色區間預測建模理論,利用灰色區間預測方法中的包絡帶預測[15],充分考慮軌道高低不平順的動態隨機性和異質性,構建重載鐵路軌道高低不平順(特指軌道整體不平順)的灰色區間預測模型,并根據神朔鐵路實際檢測數據進行建模分析,擬合神朔鐵路軌道高低不平順的變化規律,對模型的有效性、可靠性進行實例驗證。
1 軌道高低不平順的灰色區間預測模型構建
1.1 軌道高低不平順特征及建模思路
軌道高低不平順具有動態隨機性和異質性等特征。如圖1所示為神朔鐵路上行2015年8月、9月K3+800~K102+000里程范圍內的兩次軌道左、右高低不平順變化情況,從圖1可以看出,在不同里程位置上其變化規律不同,這說明了軌道高低不平順變化的異質性。

圖1 神朔鐵路上行2015年8月、9月K3+800~K102+000高低不平順值
動態隨機性和異質性等特征與灰色系統的特點非常吻合,本文選擇灰色系統的理論和方法來研究重載鐵路軌道高低不平順,對重載鐵路軌道高低不平順振蕩序列構建灰色區間預測模型,以探求其潛在的隨時間的變化規律并預測未來的數值。以神朔鐵路為例,通過將神朔鐵路連續的軌道線路按照200 m的單元長度劃分成若干連續的單元線路區段[1,16],針對不同單元線路區段基于灰色區間預測方法進行個性化建模,利用各線路區段歷史軌道高低不平順檢測數據對模型進行驗證。
1.2 軌道高低不平順的灰色區間預測模型
灰色區間預測建模方法是通過對振蕩幅度大的小樣本(一般指樣本量小于30)原始序列的上下界序列直接建立非等間隔GM(1,1)模型,得到原始序列區間預測值和基本預測值,建立區間預測算法[17]。

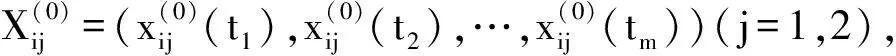
(1)間距序列:Δt=(Δt1,Δt2,…,Δtm),其中,Δt1=1,Δtk=tk-tk-1,k=2,3,…,m。

(1)

k=1,2,…,m-1
(2)
進一步得神朔鐵路線路區段i的原始軌道左(右)高低不平順序列在tn+k的區間預測值[17]為
(3)
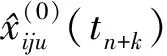
(4)

(5)
則神朔鐵路線路區段i的原始軌道左(右)高低不平順序列在tn+k的預測值為
(6)
1.3 模型精度檢驗
為判斷所建灰色區間預測模型的可靠性,計算上下界序列的模擬誤差和平均相對誤差,評估模型的精度等級[18]。精度檢驗等級參照如表1所示。

表1 精度檢驗等級參照
2 模型結果分析
2.1 數據準備
通過統計分析2015年7月~2016年11月神朔鐵路上行河西運輸段轄內K3+800~K102+00各單元區段每月檢測一次的軌檢車檢測數據發現,軌道不平順局部超限[19](包括左高低、右高低、左軌向、右軌向、軌距、水平、三角坑共7項單項指標超限)共計13 910處,高低不平順超限4 532處,占軌道不平順局部超限總數的32.58%,其中高低不平順Ⅰ級超限4 105處、Ⅱ級超限425處、Ⅲ級超限2處。其中,高低不平順超限病害數量最多的10個單元區段如表2所示。
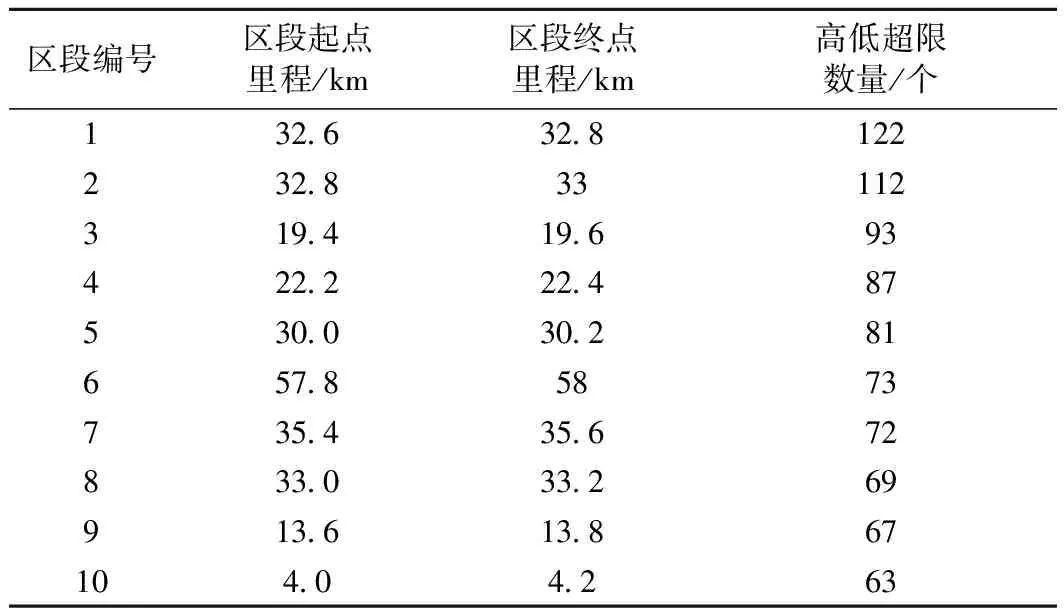
表2 神朔鐵路上行K3+800~K102+00高低超限病害高發單元區段
以表2中的10個高低超限病害高發單元區段為模型驗證對象,選取其2015年7月~2016年11月共17次的軌道高低不平順檢測數據進行模型驗證,并以單元區段K32+600~K32+800(區段編號1)為例說明建模過程。表3為區段1的歷史軌道高低不平順檢測數據。
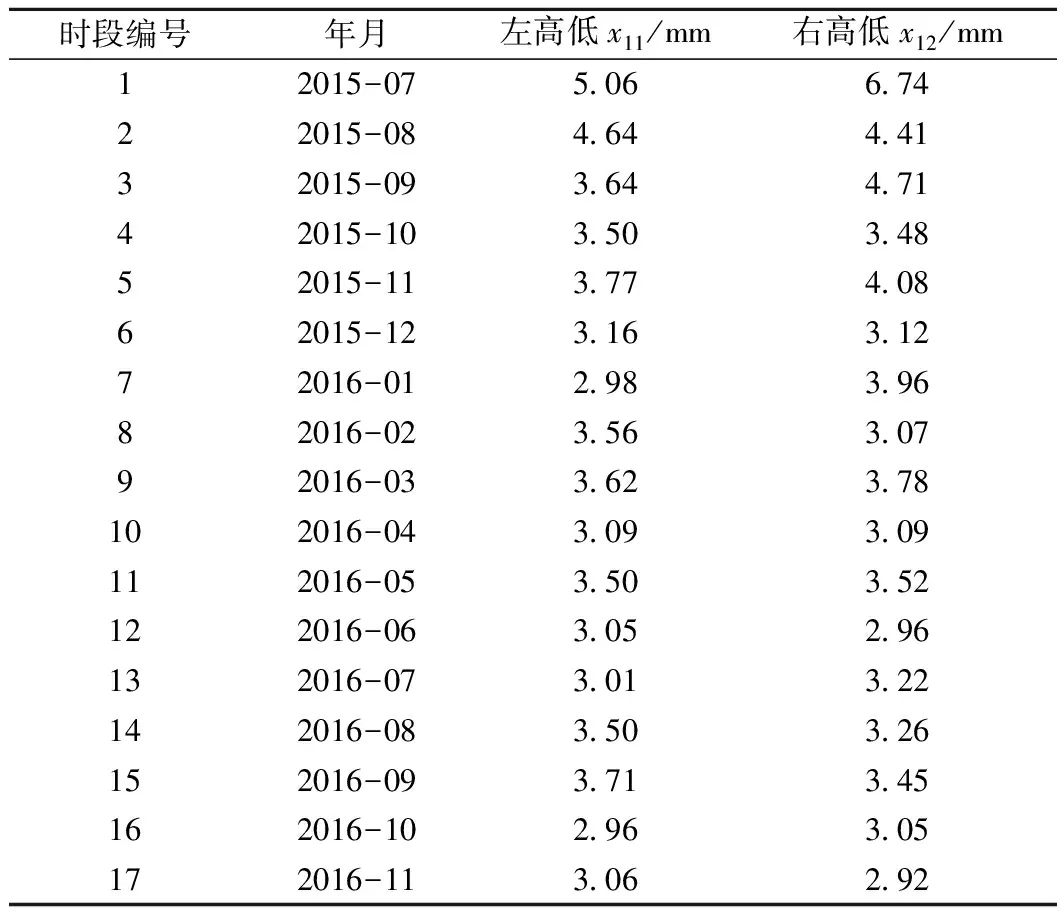
表3 2015年7月~2016年11月區段1軌道高低不平順檢測數據
2.2 模型結果

采用上下限線劃分法選取區段1軌道左、右高低不平順的上下界序列,分別為
區段1左、右高低不平順的的上下界序列的時間響應式分別為
(7)
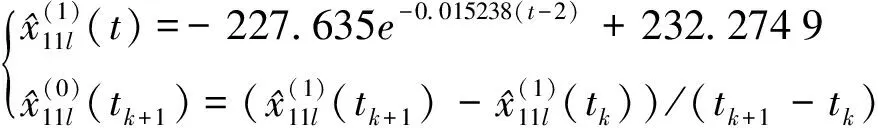
(8)

(9)

(10)
運用以上模型分別計算出2015年7月~2016年10月區段1的軌道左、右高低不平順上下界序列的擬合值。擬合結果如表4及表5所示。對左高低不平順上下界擬合的平均相對誤差分別為0.023 5和0.036 9,精度均為二級,可較好地模擬左高低不平順的發展變化;對右高低不平順上下界擬合的平均相對誤差分別為0.032 9和0.030 4,精度均為二級,可較好地模擬右高低不平順的發展變化。

表4 區段1軌道左高低擬合結果

表5 區段1軌道右高低擬合結果
基于上述預測模型(7)~(10),預測神朔鐵路上行2016年11月K32+600~K32+800單元區段(區段1)的軌道左、右高低不平順值,并與實際值進行對比,結果見表6。

表6 2016年11月區段1軌道左、右高低不平順預測值與實際值對比結果
通過表6可以看出,2016年11月區段1軌道左、右高低不平順的實際值3.06、2.92都分別在上、下界序列預測值構成的預測區間[2.781 1,3.546 2]、[2.854 2,3.037 6]內,且實際值與預測值的相對誤差分別僅為-0.033 9、-0.008 9,說明模型可以較好地預測未來的軌道左、右高低不平順值。
同理,對區段2~區段10的軌道左、右高低不平順檢測數據分別建立灰色區間預測模型,各區段模型擬合精度見表7。由表7可知,各模型精度均為二級及以上,可較好地模擬軌道高低不平順的發展變化。2016年11月的預測結果見表8。

表7 2015年7月~2016年10月區段1~區段10軌道高低不平順擬合精度
通過表8可以看出,2016年11月區段1~區段10的軌道左、右高低不平順的實際值均分別在其上、下界序列預測值構成的預測區間內,且實際值與預測值的相對誤差都較小,進一步說明本文構建的基于灰色區間預測模型的重載鐵路軌道高低不平順預測模型,可以較好地預測未來的軌道左、右高低不平順值。
通過對不同單元線路區段個性化建模發現,各模型參數及預測值具有較大差異,較好地反映了異質性,且通過模型驗證,發現各區段預測模型都具有較高精度,表明所建模型可以較好地解決軌道高低不平順預測動態隨機性問題。

表8 2016年11月區段1~區段10軌道高低不平順預測結果
3 結語
(1)以200m為單元線路區段,針對重載鐵路軌道高低不平順建立了灰色區間預測模型,并基于神朔鐵路上行10個高低超限病害高發單元區段的歷史軌道高低不平順檢測數據,對所建軌道高低不平順的灰色區間預測模型進行了實例驗證,驗證結果表明,所建模型可以較好地用于預測重載鐵路軌道高低不平順值。
(2)軌道高低不平順具有異質性,故需要根據實際情況選取適當的高低不平順數據序列長度及相應的上下界序列,針對不同區段建立相應灰色區間預測模型,并需要隨著數據量的積累修正模型。未來筆者將利用神朔鐵路軌道高低不平順變化規律及其預測值,進一步研究神朔鐵路線路搗固等維修作業計劃的編制問題。

