基于不同基礎模擬方式的鋼-混凝土組合高架獨柱車站抗震分析探討

馬福東

(中鐵工程設計咨詢集團有限公司，北京 100055)

近年來，城市軌道交通進入了快速發展的階段，高架軌道以其占地少、建造周期較短、建設費用較節省等特點，在城市軌道交通中廣泛運用[1-2]。特別是隨著各項技術的日趨成熟，新型跨座式單軌以其獨特的靈活性、顯著的經濟性和優良的適用性等特點而得到領域內人士廣泛認可，正在逐步成為二、三線城市的主要交通制式，從而進一步推動了高架軌道的高速發展。無論是鐵路、傳統軌道交通還是新型跨座式單軌，高架車站是高架軌道交通中的重要組成部分，其中“站橋合一”高架車站占地面積小，不影響地面綠化，空間利用率高，在高架車站的建設中被廣泛采用[3-4]。高架車站的設計涉及鐵路、城市軌道交通兩個領域的建筑、結構、橋梁等多個交叉行業，不同的行業有不同的行業標準，結構設計時采用哪種行業標準，不同的行業標準存在哪些差異，這些是值得研究的問題。

在城市軌道交通高架線路中，盡管獨柱墩車站的側向剛度偏弱，抗震冗余度較低，因其“上大下小”的結構特點不利于結構抗震[2，5]，但由于其良好的景觀性和道路適應性，獨柱車站仍然是路中車站的重要選型方案[6]。因此獨柱車站的抗震分析設計顯得格外重要，應針對關鍵構件進行抗震性能設計[7]，提高其結構體系中重要構件的抗震性能。這就有必要對不同規范、不同基礎模擬方式下，獨柱車站體系中的重要構件的抗震分析結果進行分析探討。

民用建筑設計中，計算結構的地震反應時，一般將基礎頂面設為剛接進行計算，必要時也按考慮樁基剛度采用等效彈簧模擬的模型進行計算；而城市軌道交通規定高架車站結構中承受列車荷載的結構，設計地震作用基準面宜取在樁基礎的樁尖位置，同時樁土作用的考慮方法也與民用建筑規范不同。本文通過某高烈度區的獨柱車站工程實例，分析以上兩種規范對基礎不同模擬方式的計算差異，并給出相應的設計建議。

1 工程概況

某跨座式單軌工程位于廣東省汕頭市，其中某車站為路中高架兩層側式站，站臺寬約4.5 m。車站規模為71.0 m×15.58 m，建筑面積為1 730 m2。車站采用新型獨柱大懸挑鋼-混凝土組合框架結構，縱向柱距為14.2 m，共6軸，框架柱采用鋼管混凝土柱，橫向框架梁采用鋼管混凝土組合梁，兩側懸挑長度為7.79 m，其余梁均采用鋼梁，樓板采用混凝土板。站頂雨棚采用輕型鋼結構。

鋼-混凝土組合獨柱車站結構與傳統鋼筋混凝土獨柱車站結構相比，充分利用了鋼材和混凝土各自的材料特性，組合構件尺寸小，站臺層凈空以及地面使用空間均大大增加，結構形式輕盈美觀；同時自重輕，地震作用減小[8]，有更強的抗震能力及變形能力[9]，更有利于實現輕量化的設計目標；構造簡單，節省支模工序和模板，現場施工周期縮短，對城市交通影響周期短。綜上所述，由于組合結構的優勢，在城市軌道交通的建設中，鋼-混凝土組合結構是一種具有廣闊應用前景的結構方案。

本項目車站主體結構設計使用年限為100年，建筑結構安全等級為一級，結構重要性系數為1.1。抗震設防烈度為8度，設計基本地震加速度為0.20g，設計地震分組為第二組；建筑場地類別為Ⅱ類。抗震設防類別為重點設防類；抗震等級為框架結構一級。車站主體采用鋼-混凝土組合獨柱車站結構，矩形鋼管混凝土獨柱截面尺寸為B1600 mm×2 000 mm×46 mm×46 mm(縱向×橫向×壁厚×壁厚)，矩形鋼管混凝土長懸臂蓋梁主要截面尺寸為B2 000 mm～1 000 mm×1 600 mm×28 mm×35 mm(高度×寬度×腹板壁厚×翼緣壁厚)，縱向連系鋼梁截面尺寸為B950 mm×400 mm×20 mm×30 mm(高度×寬度×腹板壁厚×翼緣壁厚)。車站主體平面及橫剖面見圖1、圖2。

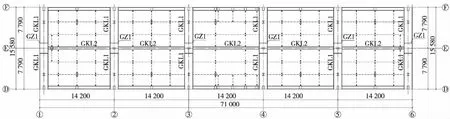
圖1 車站主體結構平面(單位：mm)

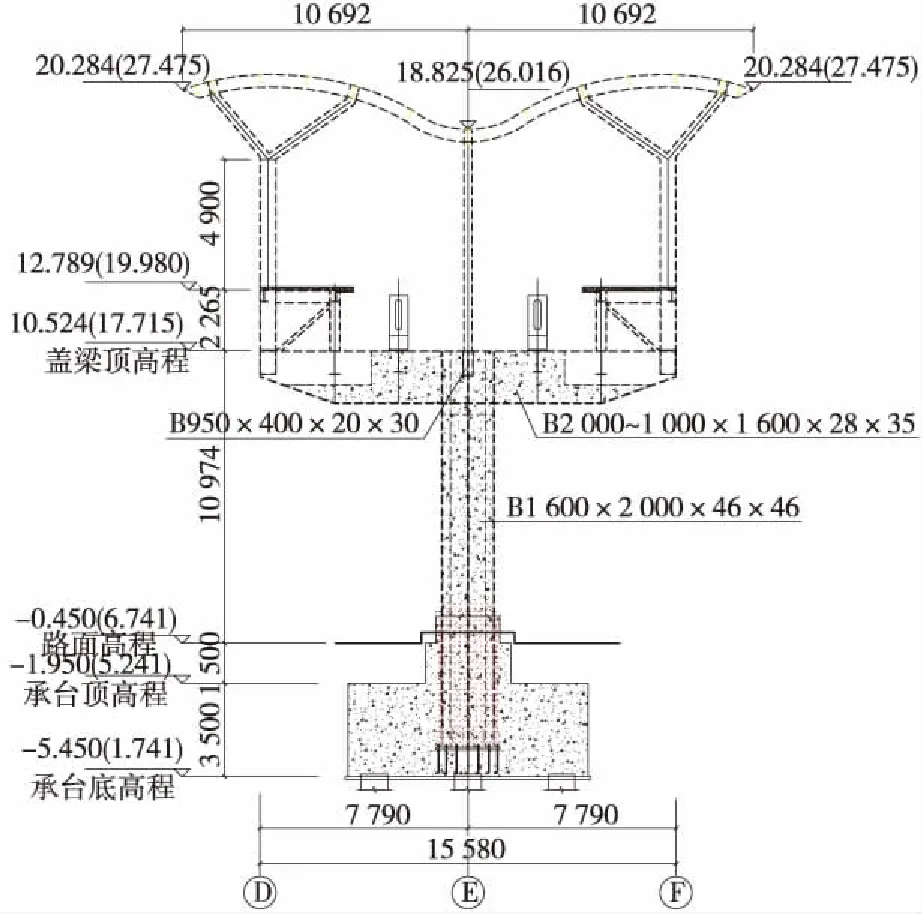
圖2 車站結構橫剖面(單位：mm)

2 結構分析

結構分析模型采用不同的基礎模擬方式，即不考慮和考慮樁土相互作用，并采用不同的規范考慮土對樁的約束作用。采用Midas Civil軟件建立車站整體空間有限元對比分析模型，如圖3所示。

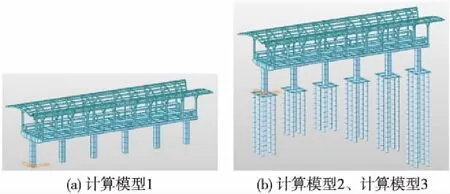
圖3 三維計算模型

本項目基礎采用柱下獨立樁基承臺，基樁采用鉆孔灌注樁。各柱承受的荷載較大，根據地質條件及承載性狀，基樁屬于摩擦端承樁。經過樁承載力計算，選用1.0 m的樁徑，由于擬建場地的基巖面起伏變化較大，有效樁長20～35 m，樁端進入基巖1 m。

以下模型中僅對基礎采用不同的處理方式進行對比分析，其他設計條件均相同。計算模型編號如下所示，結構順橋向為X向，橫橋向為Y向。

(1)計算模型1：不帶樁，基礎頂面為剛接，如圖3(a)所示。

(2)計算模型2：帶樁，承臺及樁采用等效彈簧模擬的模型，如圖3(b)所示，樁土作用按《建筑樁基技術規范》定義。

(3)計算模型3：帶樁，承臺及樁采用等效彈簧模擬的模型，如圖3(b)所示，樁土作用按《城市軌道交通巖土工程勘察規范》(GB50307—2012)定義。

3 樁土作用分析

樁土相互作用主要是土對樁有水平約束，可采用線性彈簧考慮樁側摩阻和樁端摩阻對樁的約束作用[10]。根據《城市軌道交通結構抗震設計規范》(GB50909—2014)，采用彈性反應譜方法和彈塑性反應譜方法時，基礎與地基土的相互作用按照樁基礎集中參數法[11]，詳見圖4，土彈簧采用理想彈塑性本構模型。

注：kh——樁側水平地基彈簧初始剛度；ksv——樁周豎向地基彈簧初始剛度；kv——樁尖豎向地基彈簧初始剛度；khf——承臺側面的水平地基彈簧初始剛度。圖4 樁基礎集中參數模型

3.1 樁土彈簧剛度定義

樁基礎的地基彈簧剛度按以下所列各式計算：

樁側水平地基彈簧初始剛度

kh=KhDΔl

樁周豎向地基彈簧初始剛度

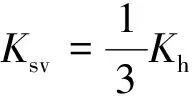
樁尖豎向地基彈簧初始剛度

kv=KvAv

承臺側面的水平地基彈簧初始剛度

khf=KhAf

式中Kh——樁側水平基床系數，kN/m3，取計算位置的基床系數K;

Ksv——樁周豎向基床系數，kN/m3；

Kv——樁尖豎向基床系數，kN/m3，取計算位置的基床系數K；

Δl——計算范圍內樁的長度，m；

D——樁的直徑或寬度,m；

U——樁截面周長,m；

Av——樁尖面積，m2；

Af——承臺側面的面積，m2。

3.2 基床系數

當基床系數無靜載試驗資料時，《建筑樁基技術規范》(JGJ94—2008)與《城市軌道交通巖土工程勘察規范》(GB50307—2012)對于基床系數經驗取值存在差異。

《建筑樁基技術規范》(JGJ94—2008)將土體視為彈性介質，其水平抗力系數(等價為水平基床系數)隨深度線性增加(m法[12])，與水平抗力系數的比例系數m值成正比。《城市軌道交通巖土工程勘察規范》[13]中對于不同的巖土類別給出基床系數經驗值，不隨深度的變化而變化。

3.3 樁土彈簧剛度取值

計算模型2和計算模型3根據不同規范計算樁身不同高度位置的彈簧剛度選取詳見表1，限于篇幅表1中僅列出不同土層的典型值。

表1 不同規范的樁土彈簧剛度

由表1可知，按《建筑樁基技術規范》(JGJ94—2008)m值法計算的彈簧剛度大于按《城市軌道交通巖土工程勘察規范》(GB50307—2012)的計算值，越到樁的下部，差值越大，最大差異約為100倍。

4 計算結果分析

針對以上的計算分析模型，采用振型分解反應譜法，進行結構的小震彈性分析，比較不同模型計算結果的差異，并分析其原因。

4.1 模態分析結果

3種計算模型的前三階周期振型如表2所示。

由表2可知，3種計算模型的振型規律基本一致，均為第一階振型Y向平動，第二階振型扭轉，第三階振型X向平動。由于兩個方向的受力特點和剛度存在差異，結構扭轉反應較大。

相關研究表明，與剛性地基相比，考慮土-結構相互作用，使體系的基頻降低、自振周期延長[14]。本文分析也表明結構的自振周期隨著基礎約束的減弱而增大。模型2和模型3的第1階周期約為剛接模型的109%和122%；第2階周期約為剛接模型的110%和122%；第3階周期約為剛接模型的104%和112%。3種計算模型的平動和扭轉的周期比均小于0.9。

表2 周期振型

4.2 基底剪力

3種計算模型的基底剪力如圖5所示。

由圖5可知，模型2和模型3的基底剪力明顯大于剛接模型的基底剪力，結構的基底剪力隨著基礎約束剛度的減弱反而增大。模型2和模型3順橋向的基底剪力約為剛接模型的106%和112%；橫橋向的基底剪力，模型2和模型3基本一致，約為剛接模型的108%。

圖5 3種計算模型的基底剪力對比

以上對比結果主要由兩個原因造成。其一，由于帶樁基的模型，考慮了承臺和樁的質量，承臺與樁均參與到地震分析中，這是導致結構的基底剪力隨著基礎約束剛度的減弱反而增大的主要原因；其二，與模型1相比，模型2、模型3為帶樁模型，模型中模擬樁的彈簧剛度越弱，周期越長，頂層位移就越大，同時形成了頂層結構的鞭梢效應，地震作用效應增大。剛接模型的計算較實際偏小，表明不考慮樁土作用將會低估實際地震反應，使結構偏不安全。

4.3 首層層間位移角

3種計算模型的首層層間位移角如圖6所示。

圖6 3種計算模型的層間位移角對比

相關研究表明，地震激勵作用下，隨著基礎剛度的增大，橋梁墩頂位移呈較明顯的減小趨勢[15]。由圖6可知，結構的層間位移角隨著基礎約束的減弱而增大。模型2和模型3橫橋向的層間位移角約為剛接模型的120%和144%，順橋向的層間位移角約為剛接模型的123%和165%。3種計算模型的層間位移角均滿足規范限值1/550。

結構首層層間位移角的變化規律與結構自振周期的變化規律一致，考慮樁土作用，結構整體剛度變柔，結構的層間位移角變大。結果表明不考慮樁土作用會低估結構的變形反應，使結構偏不安全。

4.4 關鍵構件內力

選取恒載、地震單獨作用工況和地震組合工況(1.2×(1.0恒+0.5活)+1.3Eh+0.5Ev)為代表工況，來考察3種計算模型的關鍵構件內力的差異。限于篇幅，本文僅選取邊跨和中跨兩個比較有代表性的梁柱內力值。

4.4.1 墩柱

邊跨1軸、中跨4軸墩柱柱底內力詳見表3。

由表3可知：

恒載作用下，3種模型的柱底內力基本一致。

橫橋向地震組合工況下，邊柱模型3的柱底剪力和彎矩約為剛接模型的121%和114%，中跨各軸內力大多與剛接模型差值較小。

順橋向地震組合工況，邊柱柱底剪力隨著基礎約束的減弱而增大，模型2和模型3的柱底剪力約為剛接模型的105%和114%，模型3的柱底彎矩約為剛接模型的111%，中跨各軸內力與剛接模型的差值相對較小。

從各墩柱地震作用下的柱底剪力可知，各個墩柱剪力的變化規律與結構基底剪力的變化規律一致。

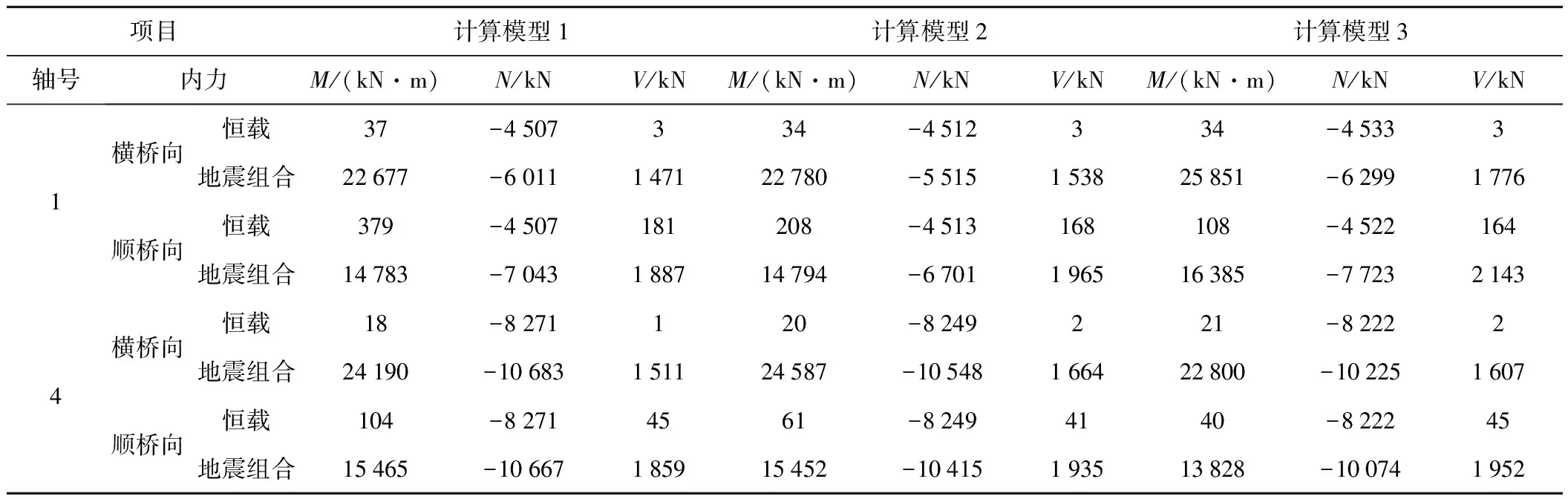
表3 3種計算模型相同荷載工況下的柱底內力

注：彎矩M、剪力V方向與順、橫橋向相對應；軸力N受拉為正，受壓為負。

4.4.2 蓋梁

邊跨1軸、中跨4軸蓋梁梁端內力詳見表4。

由表4可知：恒載作用下，3種模型的兩端彎矩和剪力基本一致。橫橋向地震組合工況下，中部蓋梁梁端內力差值很小；邊部蓋梁模型2和模型3的梁端剪力約為剛接模型的102%和118%，模型2和模型3的梁端彎矩約為剛接模型的101%和116%。

表4 3種計算模型相同荷載工況下的梁端內力

5 結論及設計建議

5.1 主要結論

通過以上3種計算模型的分析對比，有如下結論。

(1)帶樁模型與不帶樁模型的模態振型規律基本一致。與剛性地基相比，考慮樁土共同作用，使結構體系的自振周期延長、變形反應加大；且結構的自振周期以及變形反應隨著基礎約束的減弱而增大。

(2)結構的基底剪力隨著基礎約束剛度的減弱反而增大，主要由兩個原因造成。其一，由于帶樁基的模型，考慮了承臺和樁的質量，承臺與樁均參與到地震分析中，這是導致結構的基底剪力隨著基礎約束剛度的減弱反而增大的主要原因；其二，與剛性地基相比，考慮樁土相互作用時，模型中模擬樁的彈簧剛度越弱，周期越長，頂層位移則越大，同時形成了頂層結構的鞭梢效應，地震作用效應增大。

(3)恒載作用下，3種計算模型條件下墩柱、蓋梁的計算內力基本一致。本工程車站順橋向平面尺寸較短，扭轉效應對邊跨影響明顯。地震組合工況下，結構主要構件內力隨著基礎約束剛度的減弱一般有不同程度的增加，基礎約束的變化對中部構件的內力影響較小，對邊部構件的內力影響較大。

(4)考慮基礎剛性將低估結構的實際地震反應，采用樁土彈簧來模擬實際的基礎情況，可以提高結構安全度。

5.2 設計建議

由于獨柱結構存在的扭轉效應，在地震作用下，基礎約束的減弱會導致邊部構件內力的增加，要特別關注邊部構件的設計。基于獨柱長懸臂結構體系的特殊性，從結構的安全可靠性出發，設計時宜考慮樁土共同作用，地震作用基準面取在樁基礎的樁尖位置，土彈簧剛度可進行包絡設計。同時，對獨柱車站的主要構件應進行抗震性能化設計。特別是對于獨柱墩，其抗震冗余度低，其抗震性能目標建議確定為大震斜截面彈性、正截面不屈服。