自升式平臺樁腿間距對波浪載荷敏感性分析
張鵬飛 周 佳,2 劉樂樂,2
(1.中國船舶及海洋工程設計研究院 上海200011;2.上海交通大學 船舶海洋與建筑工程學院 上海200030)
引 言
近年來,單柱腿自升式風電安裝船在我國沿海地區成功使用,在已獲得較大經濟利益的同時,呈現出具備更大載重能力及更深作業水深等各項新挑戰的趨勢。隨著風能等新能源的大力開發、作業水深不斷增加、承載風機的能力逐漸增大且功能性更加完善,兼備打樁、起重等綜合能力的需求,工程項目經濟性成為單柱式樁腿風電安裝船關注的新方向。作為風電安裝船最重要的強度支撐結構-樁腿,由于其本身材料等級高、板厚大、加工精度要求高、造價高等因素,樁腿的優化設計對平臺的安全性及經濟性起著舉足輕重的作用。本文著重針對樁腿所受載荷進行分析,利用優化分析軟件研究樁腿間距對樁腿所受波浪載荷的影響,從而尋求更經濟的樁腿布置方案。
1 簡 介
在自升式平臺樁腿受力分析中,需考慮平臺在各種工況下所承受的靜載荷及環境載荷。靜載荷包括自重、可變載荷;環境載荷包括風浪流及慣性載荷等。靜載荷與船體的尺度、功能直接相關。環境載荷與目標船擬定工作海域相關,因此對樁腿結構強度來說,其承受的外載荷基本確定,但不同的樁腿間距、直徑卻會產生不同的承載能力。經分析及計算驗證,往往可以通過優化4條樁腿間距來降低同等周期波高特征值產生的波浪載荷對樁腿的影響。
本文通過數值分析方法找到波浪周期、波高等設計參數對樁腿產生的波浪載荷數值間的關系以及平臺樁腿橫向與縱向間距布置與波浪載荷大小的關系,從而盡可能從平臺布置優化角度降低波浪載荷對樁腿整體強度的要求[1-2]。
2 設計基礎
目標平臺長105 m、寬42 m、作業水深50 m、作業氣隙為6 m、左舷尾部布置1 300 t繞樁吊;4條樁腿左右舷對稱布置,樁腿縱向間距62 m,橫向間距31.8 m。通過使用DNV-Sesam軟件建立平臺梁系有限元模型(圖1);環境載荷作用角度分為0°、28°(樁腿對角線連線與船長方向夾角)[3]、62°、90°、118°、152°和 180°(見圖 2)。由于本船繞樁吊布置在左后樁腿上,經樁腿強度計算分析得到,左后樁腿往往先達到最大屈曲狀態,且發生最大屈曲時,環境載荷通常為90°或118°環境條件時。故本文主要針對這兩個方向環境載荷作用工況進行分析。
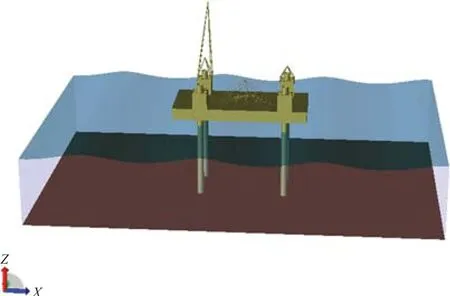
圖1 有限元模型
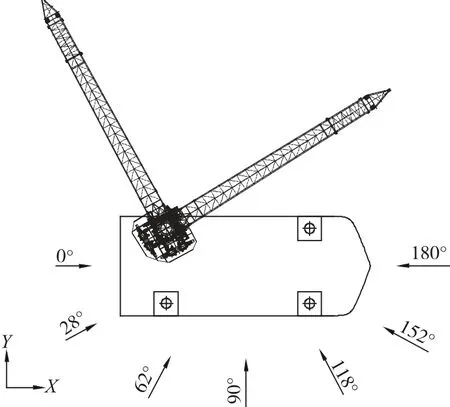
圖2 環境載荷方向示意圖
總體坐標系統如下:
(1)X軸指向首部,船首為正;
(2)Y軸指向左舷,左舷為正;
(3)Z軸垂直向上,向上為正。
為研究主船體樁腿布置與波浪載荷之間的關系[4],采用優化設計軟件Optimus,在有限元分析軟件基礎上,搭建計算優化設計工作流,設定波浪載荷目標值的多次迭代計算,從而找到各個變量與波浪載荷間的關系。目標是通過使用優化算法,以最少的樣本點數量和盡可能高的精度分析設計參數與設計指標間的線性、交叉項、二階甚至更高階的相互關系,根據結果建立輸出參數的響應面;計算越多,響應面精度越高,響應面可以用來分析輸入輸出間的相互關系。優化算法包括二階全因子、三階全因子、拉丁超立方、Taguchi等20余種,本文選用拉丁超立方算法5 000次迭代計算。
Optimus軟件中建立工作流(圖3)。在工作流中依次啟動Genie軟件、讀取FEM文件、使用Sestra求解及導出波浪載荷等輸出信息等,以實現整個分析過程自動化執行并循環迭代。
優化設計中的變量參數及取值范圍參見表1。
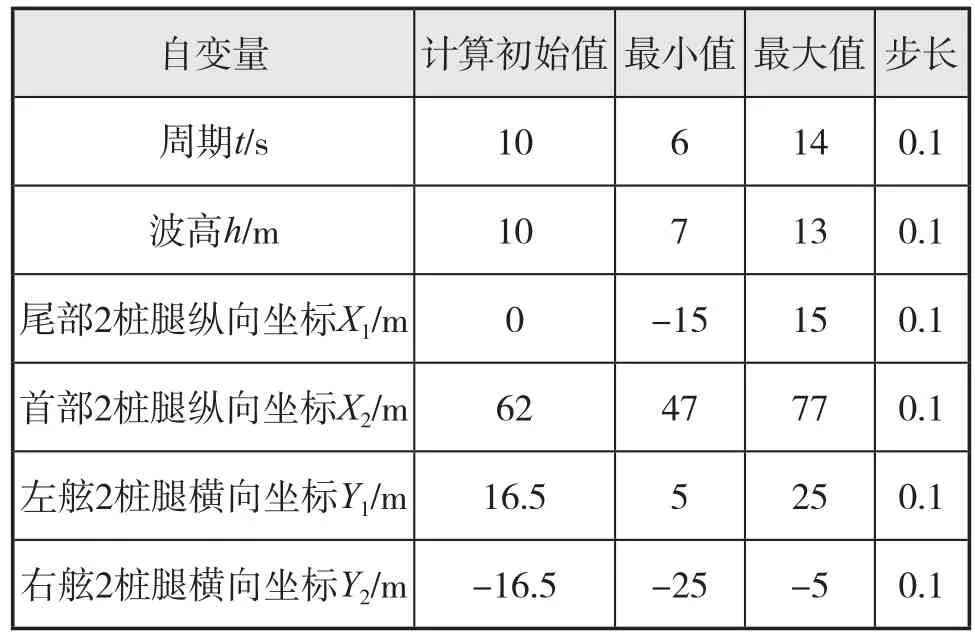
表1 變量參數及范圍
為研究周期與波高和樁腿所有波浪載荷的關系,將波高與周期設為自變量,建立響應面找到其與波浪載荷間的關系。對于優化樁腿間距的布置時,根據總體布置圖調整4條樁腿的坐標,但保證4條樁腿的連線始終處于矩形的4個頂點。
3 優化研究
通過拉丁超立方算法5 000次迭代計算,求得各變量與各角度波浪載荷間的相互關系如下。
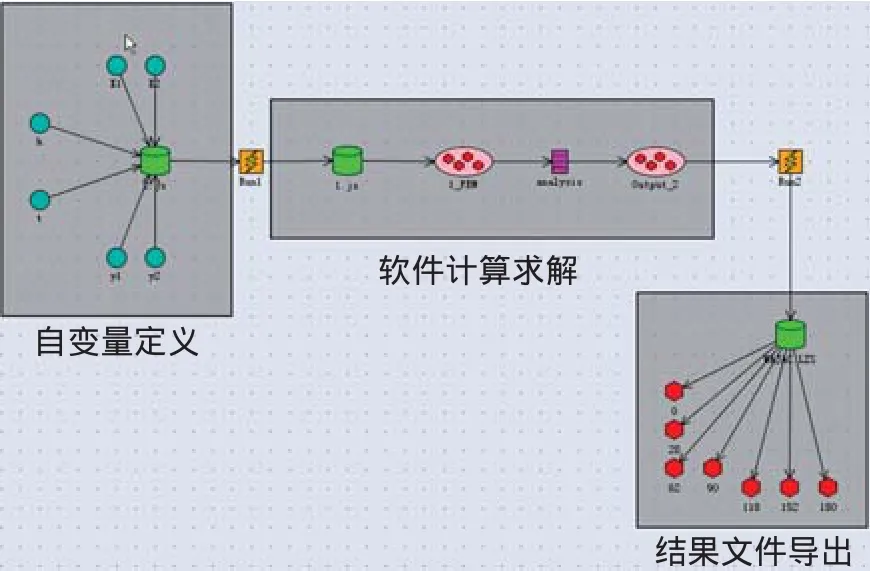
圖3 Optimus軟件中的工作流
3.1 波浪周期T、波高H與波浪載荷大小的研究
當樁腿間距固定時,T、H與波浪載荷間的關系如圖4所示。
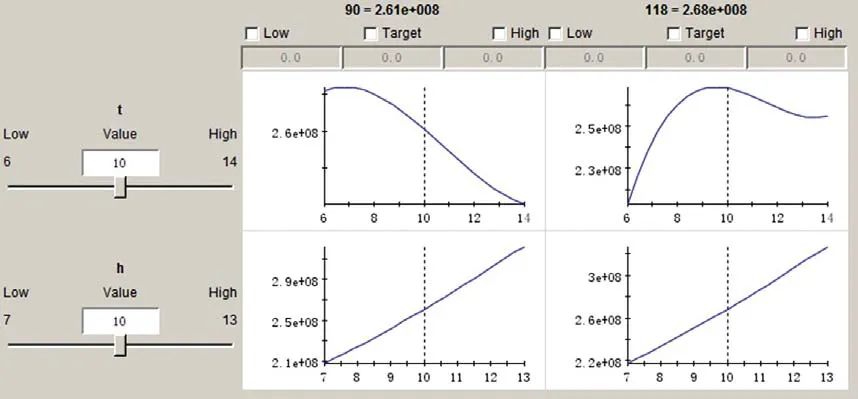
圖4 T、H與波浪載荷關系(上圖為T、下圖為H與波浪載荷關系)
由圖4可見,波高H與波浪載荷成正比關系,H越大,波浪載荷越大。(此處波浪載荷代表由波浪波高周期引起的波浪對樁腿的作用,不包括流載荷作用,下同)。
周期T與波浪載荷成正弦分布,并非周期越大波浪載荷越大,為滿足設計需要, CCS規范中規定[5],設計波波高Hmax確定后,周期應為
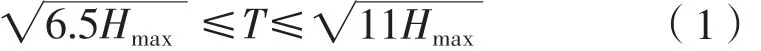
此范圍內用幾個不同的值對平臺結構應力進行估算,最終取使平臺結構產生最大應力的值。意味著存在某種波浪組合(Ta、Ha),雖然Ta< Tmax,同時Ha< Hmax,但波浪載荷對結構的影響比(Tmax、Hmax)的組合更大。由圖4獲得各浪向波浪載荷的變化如表2所示。
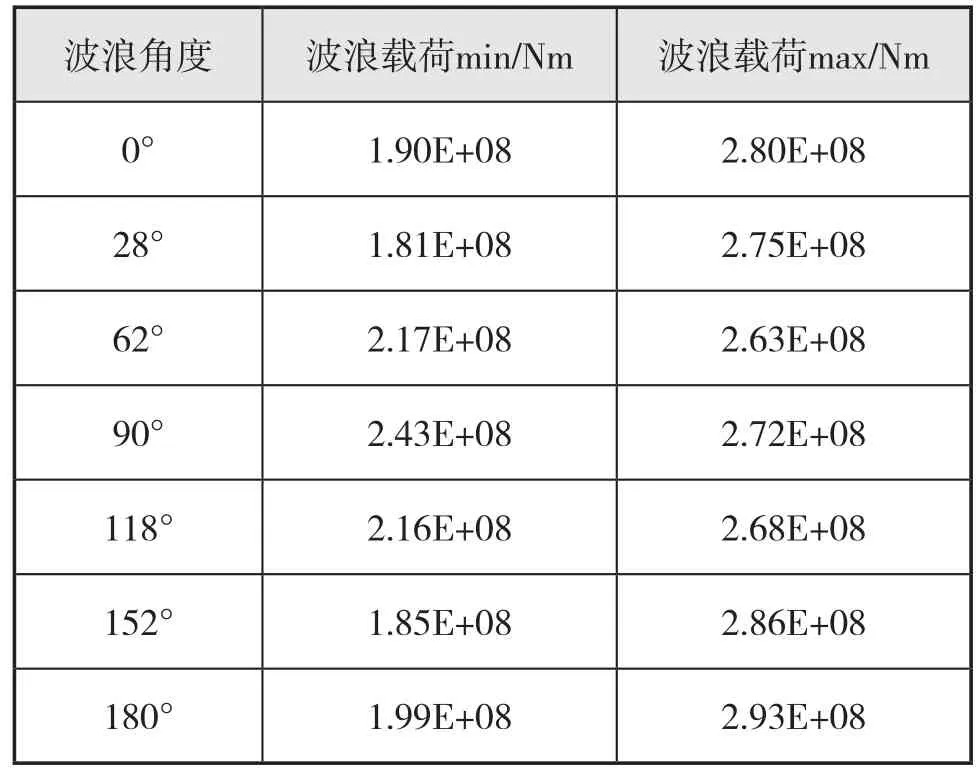
表2 波浪載荷最大值與最小值
由表2可見,波浪組合的選擇會對載荷產生很大影響,為能更好地覆蓋平臺服役期間的最大波浪載荷,應通過多次計算找到周期和波高的組合為樁腿所承受的實際波浪載荷最大值。計算研究發現對于樁腿強度計算時,給定的波浪環境載荷,應考慮指定波高H下的全概率周期范圍,盡可能考慮所有最極端情況。當樁腿間距變化時,T波浪載荷關系曲線也會發生變化,但大體趨勢相同。研究還發現,不同樁腿布置,平臺整體剛度和固有周期不同,不同周期的波浪響應不同。接近平臺固有周期的波浪載荷周期會對載荷產生更大的影響。
3.2 前后樁腿間間距(X1、X2)與波浪載荷的研究
前后樁腿的間距對波浪載荷的影響如圖5所示。
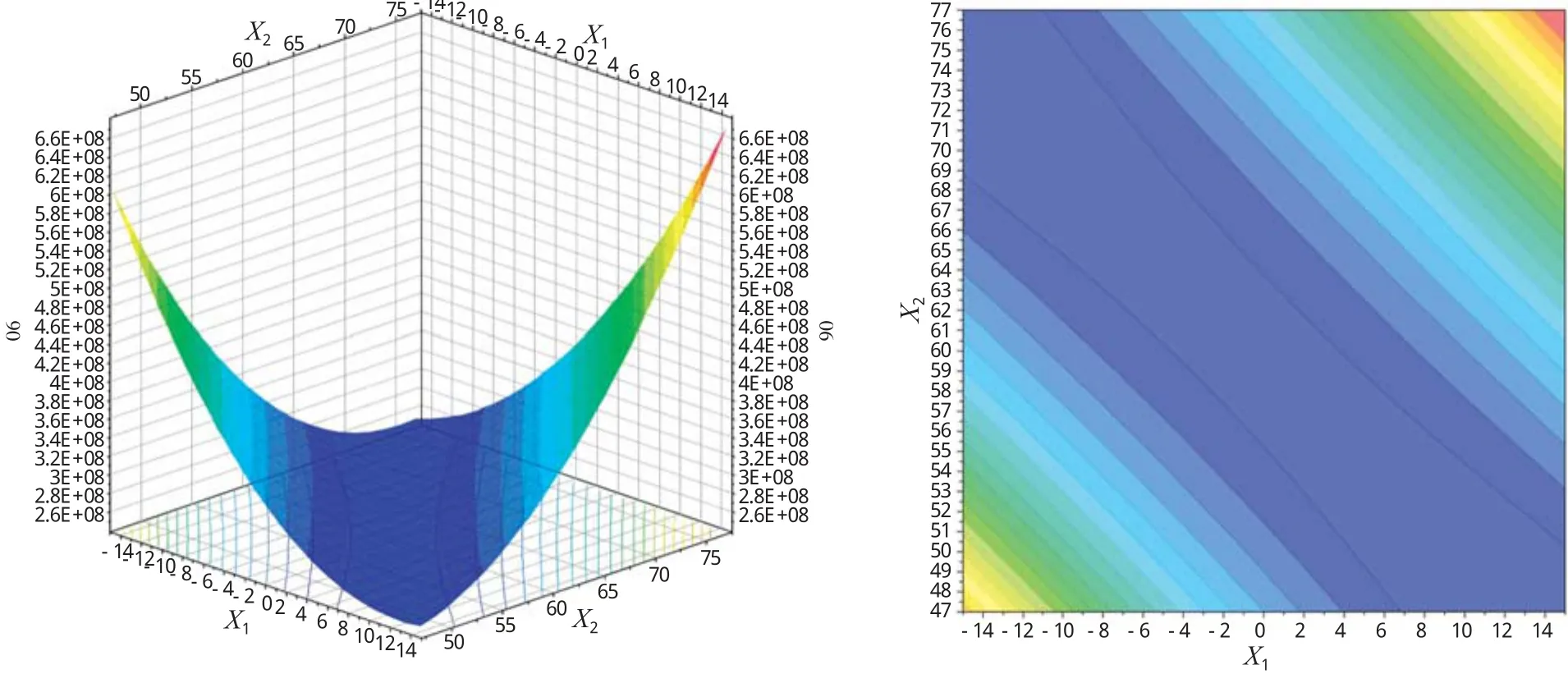
圖5 90°環境條件工況下X1、X2與波浪載荷的研究
由圖5可見,90°工況時X1與X2在響應面對角線附近,即前后樁腿間距同時增大或同時減小時,且118°工況與90°工況響應面相似。根據響應面可見,波浪載荷最大值約7.70E+08 Nm,最小值約2.40E+08 Nm。
3.3 左右樁腿間間距(Y1、Y2)與波浪載荷的研究
假定平臺長度不變時,左右樁腿的間距對波浪載荷的影響如圖6所示。
由圖6可見,波浪載荷在Y1取最大值同時Y2取最小值時趨于最小,即左右樁腿間距同時增大或同時減小時,波浪載荷值較小。且118°工況與90°工況響應面相似。對于Y1與Y2的組合情況,同樣的波浪周期與波高所產生的波浪載荷最大值約為6.2+08 Nm,最小值約為2.4E+08 Nm,相差達到2.6倍。同樣的波浪周期與波高所產生的波浪載荷顯示樁腿間距的優化對于樁腿強度計算的重要性。
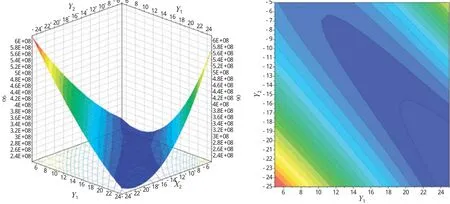
圖6 90°環境條件工況下Y1、Y2與波浪載荷的研究
3.4 X1與Y1與波浪載荷的研究
因本船繞樁吊布置于左后樁腿[6],其所在樁腿的布置與X1和Y1有關,且最大屈曲發生在此樁腿上,故針對這兩個變量進行響應面分析,尋找規律獲得最小波浪載荷,經計算求得響應面(見圖7)。
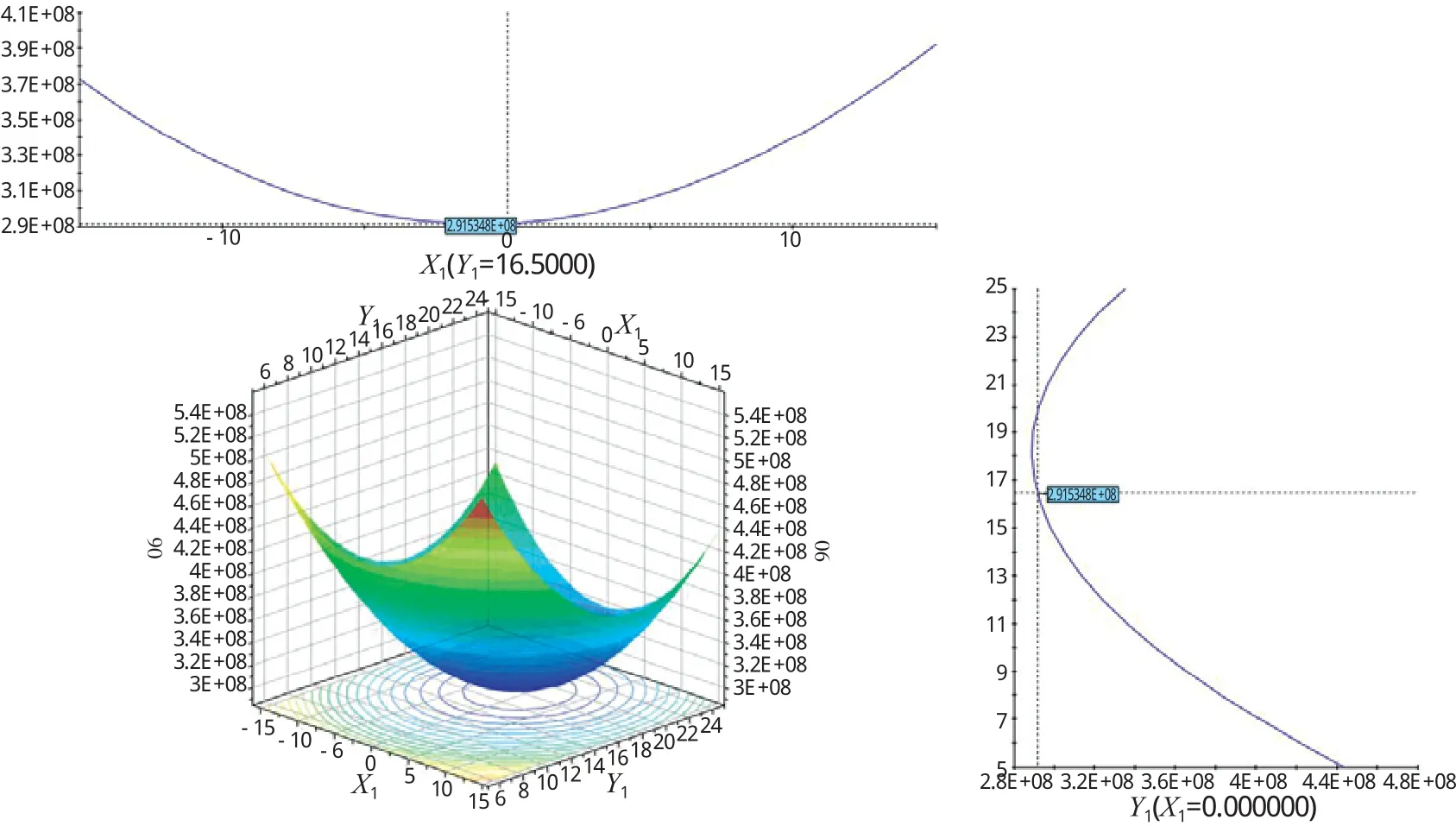
圖7 118°工況下X1與Y1對波浪載荷響應面
由圖7可見,樁腿布置在響應面最低點附近位置時,此時X1在-1 m范圍內、Y1在18 m范圍內得到最小波浪載荷,值約為2.83E+08 Nm,響應面最大值約為5.1E+08 Nm。與樁腿初始方案X1= 0、Y1=16.5的組合相比,波浪載荷降低約7%。若換作波浪載荷較大工況(如風暴自存工況等),通過優化能更顯著降低波浪載荷比例。
3.5 優化分析總結
結合優化設計可以判定,平臺在此設計工況下,樁腿的布置能很好降低波浪載荷對樁腿的作用。通過優化計算方法,利用梁系模型能合理有效地找到波浪載荷最大值,且能通過改變樁腿布置更好地避開波浪載荷峰值區域,選擇既適合平臺總布置需要又符合經濟安全原則的優化方案。
其中3.2及3.3節中優化設計得到結論為:當樁腿同時縮小距離或增大距離時,所受波浪載荷最小,也可理解為樁腿布置調整為正方形時承受波浪載荷最小。但考慮到自航船阻力的限制,針對本船的載重、氣隙、環境載荷等信息綜合考慮,再結合3.4節內容,找到適合本船的樁腿間距布置,縱向間距約為60 m,橫向間距約為36 m。
4 結 論
本文計算通過建立梁系有限元模型模擬波浪載荷對樁腿的影響,以樁腿布置為變量,樁腿所承受最小波浪載荷為目標,找到周期T、波高H的組合對于樁腿所承受波浪彎矩的相互關系,并獲得針對于本船的主尺度、氣隙高度等因素的相關規律;不排除其他船舶對于樁腿數量增加,樁腿直徑變化、氣隙高度變化等因素對波浪載荷產生的規律變化。我們通過優化設計方法,合理有效地分析得到樁腿間距變化對樁腿所受波浪載荷的相關性研究,對結果的分析獲得以下結論:
(1)波高H與波浪載荷成正比關系,周期與波浪載荷成正弦關系。
(2)在樁腿強度計算中,固定樁腿布置后,應考慮波浪載荷對船體結構影響最大的周期波高組合以及波高H對應所有周期T的可能性作為波浪載荷輸入條件進行核算。
(3)在項目方案設計開始階段,借助優化設計對樁腿布置進行調整,尤其針對風暴自存工況及作業不起重工況(這兩種工況下波浪載荷占比較大),若能通過優化設計降低板厚,則可以降低板厚,節約成本。

