“聯想”教學法在課堂教學中的運用

花玉明

[摘要]學生在學習新知時，不善于發現新舊知之間的聯系，遇到問題不能順利地從知識體系中提取所需的知識點。在“分數與除法的關系”的教學中，教師要重視新舊知識的對比，重視學生知識體系的建構，善于運用“聯想”培養學生解決問題的能力。

[關鍵詞]聯想;分數與除法的關系;新舊知識

[中圖分類號]

G623.5

[文獻標識碼]A

[文章編號] 1007-9068（ 2019） 35-0063-02

【教學案例】分數與除法的關系

1.舊知鋪墊，為學生創設“聯想”的平臺

在小學數學知識體系中，每個知識點都不是單獨存在的，知識與知識之間有著一定的聯系。因此在引入或講解新概念時，可以采用復習的方式再現一些與之相關的舊知。

比如，教學新知前復習與之有關的整數除法：將12塊月餅平均分給4人，每人得多少塊？將4塊月餅平均分給4人，每人得多少塊？然后過渡到新授部分：將1塊月餅平均分給4人，每人分得多少塊？

三個問題，不變的是數量關系，有了這個對比的經歷，學生在遇到新問題時就能自然地聯想到相應的解題思路。

2.動手實踐，為學生搭建“聯想”的橋梁

數學課程標準指出：“數學教學，要讓學生親身經歷數學知識的形成過程。”教師不應簡單地告知學生“是什么”，而應重在讓學生經歷一個豐富、生動的思維過程，知道“為什么”。

先讓學生把一張圓形紙當成一塊月餅，然后動手分一分。學生操作后，教師再借助分數的意義幫助學生理解：將1塊月餅平均分成4份，得到的每一份都是這塊月餅的1/4，也都是1/4塊。此時板書“1÷4=1/4（塊）”，就能幫助學生初步認識分數與除法的聯系。

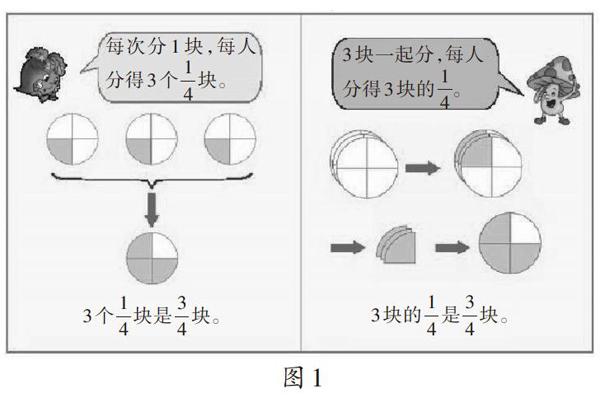
在解決“將3塊月餅平均分給4人，每人分得多少塊？”的問題時，學生可能就會聯想到利用上一個問題的解決方法去探索。在小組交流、全班思維碰撞后，教師可呈現兩種不同分法的示意圖（如圖1）。

第一種分法：將每塊月餅都分成4等份，每人都分到3個1/4塊，相當于一塊餅的3/4，即3/4塊;

第二種分法：把三塊餅疊放在一起，分成4等份，每人都分到一份，即3塊餅的1/4，這也相當于一塊餅的3/4，是3/4塊。

板書：3÷4=3/4（塊）。

繼續提出問題：“如果將3塊月餅平均分給5人，每人分得多少塊呢？”學生可以動手操作，也可以在紙上畫一畫，甚至只是在頭腦中想象。

板書：3÷5=3/5（塊）。

在動手嘗試、探究、思考后，不但新的問題得以解決，也為學生“聯想”分數與除法的關系做了鋪墊。

3.觀察比較，讓學生的“聯想”水到渠成

引導學生觀察并比較黑板上三道算式的共同點，以及每一道算式中前面的除法算式和后面的分數有什么關系，得出：被除數相當于分子，除數相當于分母，即被除數÷除數=被除數/除數。隨后，鼓勵學生想一想這個式子有沒有什么條件限制。學生可能會聯想到整數除法算式中除數不能為0的條件，那么分母不能為0就順理成章了……就這樣，一步一步地引導學生完整地歸納出分數與除法的關系。

4.應用提升，把握問題本質，為學生插上“聯想”的翅膀

在揭示分數與除法的關系后，可通過變式練習達到鞏固提升的目的。在這個環節中，教師要引導學生看清問題的本質，聯想學過的相關知識。

如，對“8千克黃豆可以榨油3千克，平均每千克黃豆可以榨油多少千克？榨l千克的油需要多少千克黃豆？”這樣的對比性練習，部分學生不分析題目中的數量關系，解題只是連蒙帶猜，結果往往不盡如人意。

在教學中要提醒學生，不能總停留在商是整數的除法的認知階段，不要總想到用大數除以小數，要聯想與問題相關聯的知識，要弄明白求平均數的數量關系，具體為“求平均每千克黃豆榨油多少千克就是用榨出的油的重量除以黃豆的重量，而求榨l千克油需要黃豆多少千克，就要用黃豆的重量除以榨出的油的重量”。列出算式后，根據分數與除法的關系，就能算出結果。

因此，把問題與已學過的知識點進行勾連，聯想到解決問題的實質，才能以不變應萬變，靈活解決問題。

【案例反思】

一、運用聯想思維溝通知識間聯系的注意點——重視知識的復習整理

在單元復習課上，盡量讓學生去翻書，在書上找出知識點，圈一圈、畫一畫，然后再把這些知識點羅列出來，找出知識間的聯系，再用圖畫、文字或表格的方式記錄下來，建構自己的知識網，然后與同學交流，完善知識結構。

這樣，在解決問題時，學生就會聯想——把一個知識點與一系列盡可能多的知識點相關聯，思維沿橫向、縱向或跳躍式地發散，學生就能以多種途徑和方式解決問題，最終有效提高分析問題和解決問題的能力。

二、建構豐富多樣的“聯想”場景

聯想思維是形象思維的具體表現，其基本的思維操作單元是表象，是一幅幅的畫面。因而，教師可創建形象化的場景來幫助學生聯想，但是要弄清新知的特點，是一個概念還是一個具體的公式，還是其他，以及在整個知識體系中的相對位置等;然后，建構與之相近、相似、相反或有因果聯系并符合學生身心特點的學習場景。這樣，學生也就容易產生聯想，并能從記憶中快速地搜索到解決問題所需的信息，并通過比較、同化等方法，把許多問題聯系起來思考，開闊了思路，得到解決問題的措施和方案。

三、多緯度觀察，聯想知識點

1.從已有經驗去聯想知識點

在學習中，學生擁有知識經驗;在生活中，學生有各種各樣的生活經驗。

例如，對于題目“爸爸每天睡7小時，他每天的睡眠時間占全天的幾分之幾？”，單位“1”是隱藏的條件，全天的時間是24小時，這是生活經驗;從知識角度講，本題需用到分數的意義這一知識經驗。這些都需要學生擁有聯想能力。

2.從方法上去聯想知識點

有些問題，可以通過聯想的作用去分析，從而得以解決。 例如，4/（ ）=8÷（ ）=0.8=（ ）/20“考查的不僅有分數與除法的關系、分數的基本性質，還有分數與小數互化的知識。首先，需要找到問題的突破口，即0.8，也就是說所有的數值都與0.8相等。根據小數的意義，可以把0.8先寫成分數8/10，再根據分數的基本性質把它化簡成4/5;根據分數與除法的關系，8/10可以寫成除法算式8÷10，根據分數的基本性質，分母乘2變成20，分子也要乘2變成16，即16/20。最后得到4/5=8÷（10）=0.8=16/20。

3.從問題形式上去聯想知識點

公式、法則、定理等存在于數學各模塊中，特殊形式和結構使它們成為數學中重要的模型。例如，對于題目“把一袋重2千克的糖果平均分給5個小朋友，每人分得這袋糖果的（）/（），是（）/（）千克。”，不少學生看完題目就感到思維混亂。歸根到底，是不理解分數所表示的兩種含義，不知道哪個是分率，哪個是具體的數量。其實，這樣的問題，從形式上看，第一個括號后面沒有單位名稱，這里的分數表示的是分率，是一種倍比關系，第二個括號后面有單位，這里的分數是一個數值，是具體的數量。前者是每人分得的糖果所占分率，由于是平均分，只要看看一共有幾人、分成了幾份，每人分得1份除以總份數5，得1÷5=1/5。對于后者，則要牢牢掌握“每人分得的數量=總數量÷平均分的份數”，即2÷5=2/5（千克）。

從以上教學案例中可以發現，聯想是解決問題的關鍵，它是新知與舊知之間的橋梁，可以有效地溝通條件與結論之間的聯系。因此，教師應立足于教材，加強知識體系的建構，設計多樣化的教學場景，多維度引導學生去聯想，通過觀察、對比、轉化、畫圖等方式幫助學生聯想，從而抓住問題的本質，尋找問題的突破口，以此實現知識的遷移，提高學生思維的應變性。

[參考文獻】

[1]趙志賢，聯想教學法在問題解決教學中的應用[J].教學與管理，2010（3）.

[2]黃金花，淺談場景模擬在小學數學教學中的運用[J].中國科教創新導刊，2013（12）.

[3] 蔣虹，有效聯想通達思維——聯想思維方法在小學六年級數學總復習中的應用[J].內蒙古教育·理論版，2015（9）.

[4] 司瑞林，談聯想思維在數學教學中的運用[J].甘肅教育，2011（ 8）.

（責編 童夏）