內可逆往復式Maisotsenko-Brayton循環生態學性能優化

沈佳鋒，戈延林，陳林根，朱富麗

(海軍工程大學, 武漢 430033)

有限時間熱力學(FTT)[1-13]理論被廣泛應用在熱力系統的分析和優化中。該理論融合了熱力學、流體力學和傳熱學等多學科內容，旨在有限時間和尺寸的限定下降低過程和循環的不可逆性，從而提升能源的利用效率。

當前大多數現存能源的生產和使用并不高效或者包含有害的環境污染物。1976年，Maisotsenko提出了一種清潔高效的熱力學循環，即Maisotsenko循環(簡稱M循環)，利用水蒸發到空氣中的潛熱提供可再生能源的方法來捕捉空氣中的能量。文獻[14]介紹了新型M循環的具體結構與循環過程。該循環不僅在暖通空調、水的蒸餾提純、電力行業和余熱回收等方面有一定程度的應用[15-19]，而且在改進燃氣輪機循環中也有應用。文獻[20]提出了M循環與Brayton循環相結合的M-Brayton聯合循環。文獻[21]證明了M-Brayton循環的熱力效率明顯高于濕空氣燃氣輪機(HAT)循環和Brayton循環。文獻[22]通過將M循環與開式的布雷頓循環結合，分析了幾種參數對燃氣輪機效率和凈輸出功率的影響。文獻[23]在M-Brayton循環的基礎上，將M循環作為底循環計算了功率和效率。文獻[24]研究了M逆布雷頓循環在低壓下的功率、效率特性。這些成果都是在經典熱力學的基礎上得到的。

文獻[25, 26]應用FTT理論建立了考慮傳熱損失的內可逆[25]和考慮傳熱損失與內不可逆性的不可逆[26]往復式M-Brayton循環模型，得到了循環的最優功率和最優效率。

1991年文獻[27]最先提出生態學函數。1992年，文獻[28]修正了生態學函數。1994年，文獻[29]給出了各種熱力循環統一的生態學函數及其品質因素的定義式。之后，生態學函數被廣泛的使用于熱機[30-32]、制冷機[33-34]和熱泵[35-37]的性能分析與優化中。

本文將在文獻[25]的基礎上，基于其內可逆往復式M-Brayton循環模型，進一步推導出循環熵產率和生態學函數等參數表達式，分析空氣飽和器中出口溫度、循環最高溫度和注水流率三種參數對循環生態學性能的影響，最后將結果與傳統的往復式Brayton循環相比較。

1 循環模型

內可逆往復式M-Brayton循環的原理圖[26]如圖1所示，圖2為其對應的圖[25]。圖1中主要的工作部件是空氣飽和器。它的工作流程為：外界空氣進入壓縮機進行絕熱壓縮；壓縮空氣進入空氣飽和器下部后，將其分成3股；3股空氣注入干通道后被水冷卻至露點溫度；兩股空氣混合后進入空氣飽和器上部，另外1股繼續在下部濕通道加熱加濕；進入上部的2股干空氣被燃氣機排放出來的廢氣加熱加濕；最后3股空氣匯合在燃燒室進行燃燒并吸熱。

內可逆往復式M-Brayton循環滿足以下4個條件[25]。

(1)T4>T3，否則空氣在飽和器下部不能被加熱加濕至飽和狀態，與設計原理不符。

(2)T6>T4，否則從空氣飽和器下部流出的飽和氣體會在上部繼續定壓放熱，不能成為過熱狀態。

(3)T8>T6，否則空氣飽和器流出的過熱濕空氣會傳熱給廢氣，不能實現回熱。

(4) 存在臨界壓比，否則當循環注水流率mwin達到飽和，會讓空氣飽和器出口的濕空氣處在兩相區，造成能源浪費。

圖1 內可逆往復式M-Brayton循環原理圖

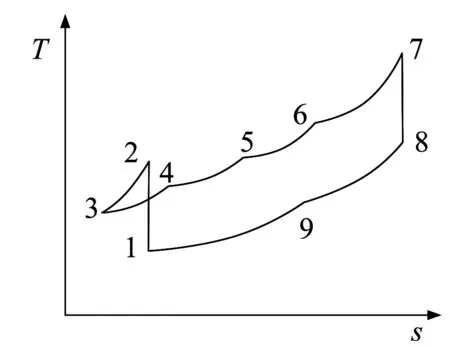
圖2 往復式M-Brayton循環圖

2 性能分析

根據濕空氣的特性，空氣中水蒸氣的壓力Ps為

Ps=αsP

(1)

αs=(ms/Ms)/(ms/Ms+ma/Ma)

式中P——空氣的總壓力；αs——空氣中水蒸氣百分數；m——質量流率；M——摩爾質量。

當空氣處于飽和或過熱狀態時，質量流率ms為

ms=0.622Ps/(P-Ps)

(2)

空氣中水蒸氣的焓ha[38]為

hs=f(Ps，T，x)

(3)

式中Ps——空氣中水蒸氣的壓力；x——干度；T——溫度。

空氣中干空氣的焓ha[39]為

ha=maCp(T-273.15)

(4)

各狀態點中蒸汽質量流率分別為

m1s=m2s

(5)

m3s=2m2s/3

(6)

m4s=(m2s+3mwinL)/3

(7)

m6s=m7s=m8s=m9s=m4s+m3s+mwinU

(8)

式中mwinL，mwinU——進入空氣飽和器下端與上端的水質量流率。

根據能量守恒定律，在飽和器上下部分通過迭代分別得到mwinU和mwinL。

不考慮壓力損失，壓氣機的壓比為

π=P2/P1=P7/P8

(9)

定義壓氣機的等熵溫比為

y=T2/T1=T7/T8=
(P2/P1)m=(P7/P8)m=πm

(10)

m=(k-1)/k

式中k——壓氣機里空氣的絕熱指數。

假設已知濕空氣流入飽和器的質量流率為m1s、壓力為P1和溫度為T1，整個過程干空氣的質量流率ma不變。根據文獻[25]，循環中濕空氣的吸、放熱率分別為

Qin=Q67=m7sh7s-m6sh6s+mah7a-mah6a

(11)

Qout=Q91=m9sh9s-m1sh1s+mah9a-mah1a

(12)

由于實際內可逆往復式M-Brayton循環中氣缸壁不是絕熱的，所以存在傳熱損失。工質和氣缸之間存在較大的溫差，必須考慮高溫濕空氣和外界環境之間的不可逆傳熱損失。假設傳熱損失正比于工質平均溫度與冷卻介質T0之間的溫差，按照文獻[40]，可表示為

(13)

式中B——汽缸壁的熱導率，J/(K·s)；T0——環境溫度。

每循環周期的輸出功率和效率分別為

P=Qin-Qout=m7sh7s-m6sh6s+mah7a-
mah6a-m9sh9s+m1sh1s-mah9a+mah1a

(14)

η=P/(Qin+Qleak)

(15)

對于內可逆往復式M-Brayton循環中存在兩種熵產：傳熱損失產生的熵產和工質經過功率沖程作功后由排氣沖程排往環境所產生的熵產。根據文獻[41]，這兩種熵產的熵產率分別為

(16)

(17)

因此，整個循環的熵產率為

(18)

循環的生態學函數[29]為

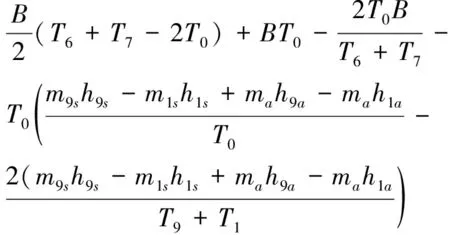
(19)

3 數值算例

根據文獻[42,43]，在計算中取Cp=1.005 kJ/(kg·K)，T1=288 K，T0=288 K，ma=1 kg/s，k=1.4，B=0.1 kW/K。通過數值計算，可以得到考慮傳熱損失時的內可逆往復式M-Brayton循環的P、η和E的特性關系。

圖3為空氣飽和器出口溫度T6對E的影響。T6=T8-20、T6=T8-25、T6=T8-30時壓比的范圍都是2～24。由圖3可知：E與壓比π為類拋物線形式，存在最大生態學函數；隨著T6的增加，E增加。

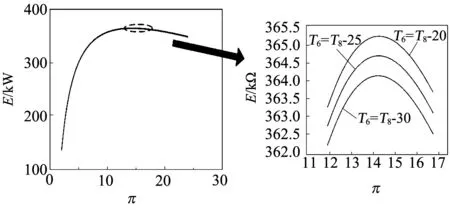
圖3 空氣飽和器出口溫度T6對E的影響

圖4為空氣飽和器出口溫度T6對E和P的影響。當T6=T8-20、T6=T8-25、T6=T8-30時，P保持不變。由圖4可知：當E小于348 kW時，E和P成類線性關系；當E大于348 kW時，每個E對應有兩個P輸出，應使循環工作在P較大的點；Emax隨著T6的增加而增加。

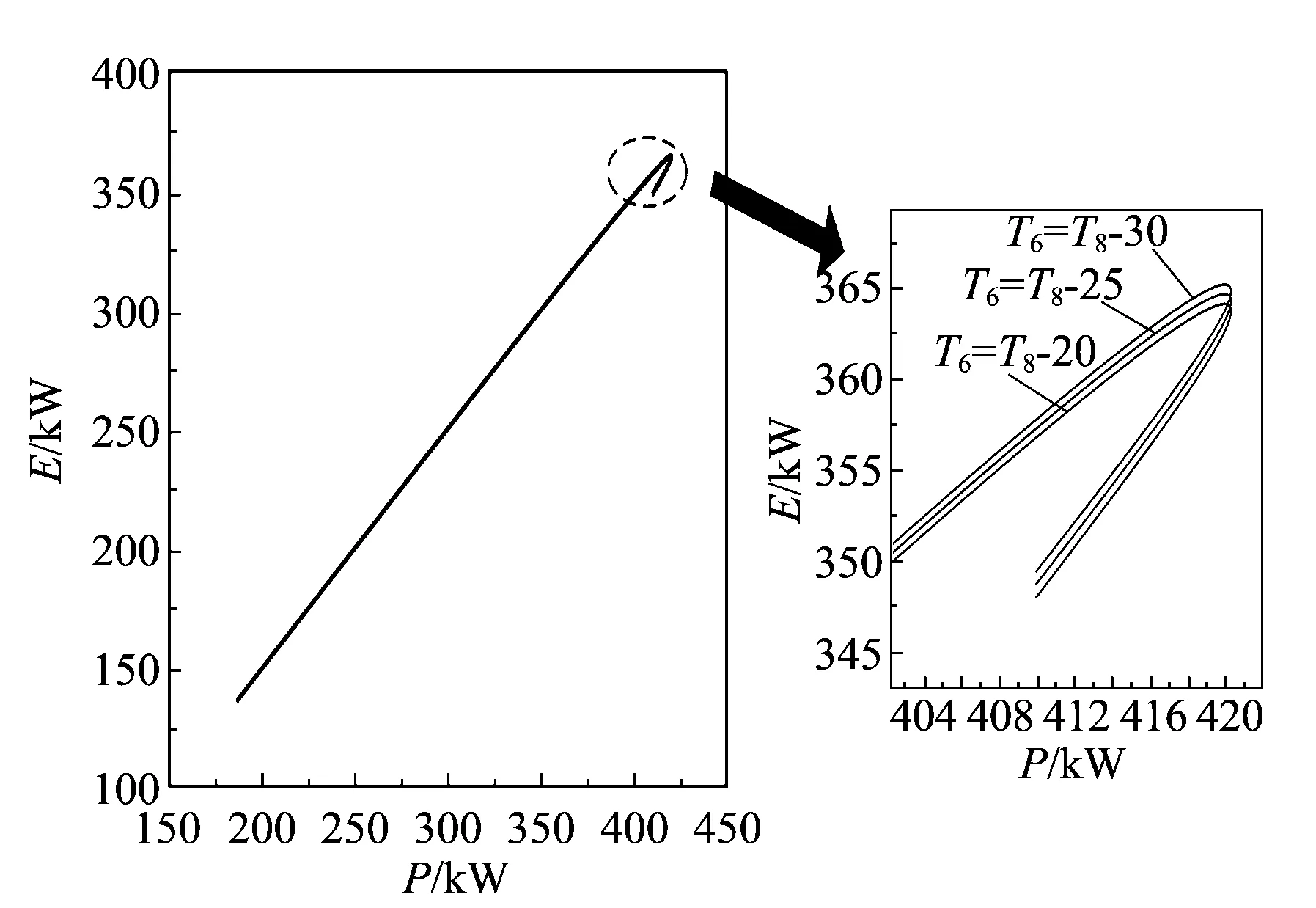
圖4 空氣飽和器出口溫度T6對E和P的影響

圖5為空氣飽和器出口溫度T6對E和η的影響。由圖5可知：當E小于348 kW時，η隨著E的減小先增大后減小；當E大于350 kW時，E對應有兩個η輸出，應使循環工作在η較大的點；E和η關系曲線存在Emax和ηmax，ηmax和Emax隨著T6的增加而增加。

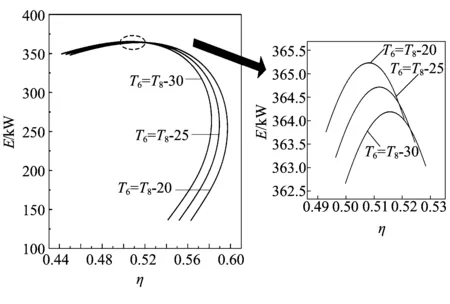
圖5 空氣飽和器出口溫度T6對E和η的影響

圖6為空氣飽和器循環最高溫度T7對E的影響。由圖6可知：1 000 K、1 100 K、1 200 K的壓比范圍都在2～33；E與壓比π呈類拋物線關系；E和Emax對應的壓比隨溫度T7增加而增加。

圖6 循環最高溫度T7對E的影響

圖7為循環最高溫度T7對E和P的影響。由圖7可知：T7不改變E和P關系曲線的基本形狀；Pmax對應的E和Emax對應的P隨著T7的增加而增加。圖8為循環最高溫度T7對于E和η的影響。由圖8可知：T7不改變E和η關系曲線的基本形狀；隨著T7的增加，E和η增加明顯；ηmax對應的E和Emax對應的η隨著T7的增加而增加。

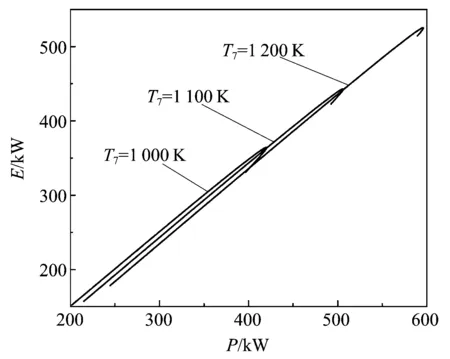
圖7 循環最高溫度T7對E和P的影響

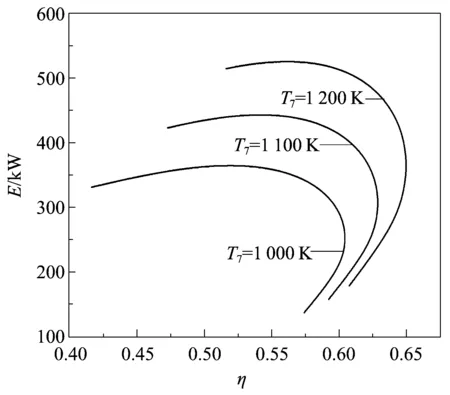
圖8 循環最高溫度T7對E和η的影響

圖9為循環注水流率mwin對E的影響。由圖9可知：在注水率mwin為0.2 kg/s時，其壓比π范圍為2～30；注水率mwin為0.3 kg/s時，其壓比π范圍為2～29；注水率mwin為0.4 kg/s時，其壓比π范圍為2～28；在此范圍內，E與壓比π呈拋物線，隨著mwin的增加，E和Emax時對應的壓比均增加。

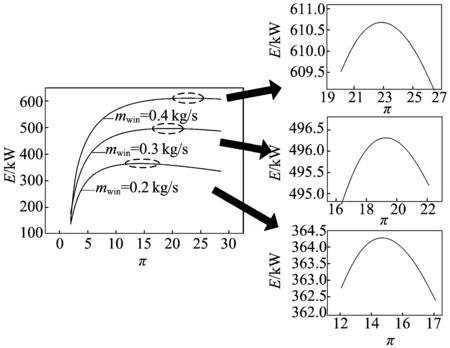
圖9 循環注水流率mwin對E的影響

圖10為循環注水流率mwin對E和P的影響。由圖10可知：mwin不改變E和P關系曲線的基本形狀；隨著mwin的增加，Pmax和Emax均隨之增加。圖11為循環注水流率mwin對E和η的影響。由圖11可知：mwin不改變E和η關系曲線的基本形狀；隨著mwin的增加，E和η增加明顯；ηmax對應的E和Emax對應的η隨著T7的增加而增加。

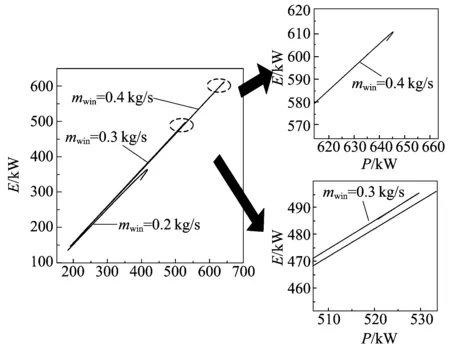
圖10 循環注水流率mwin對E和P的影響

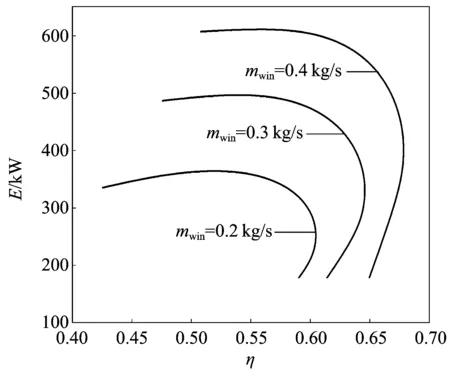
圖11 循環注水流率mwin對E和η的影響

4 與傳統往復式Brayton循環的比較

圖12為內可逆往復式M-Brayton循環與傳統往復式Brayton循環的T-s對比圖。實線為本文提出的M-Brayton聯合循環，虛線部分1-2-3B-4B-1為傳統往復式Brayton循環。

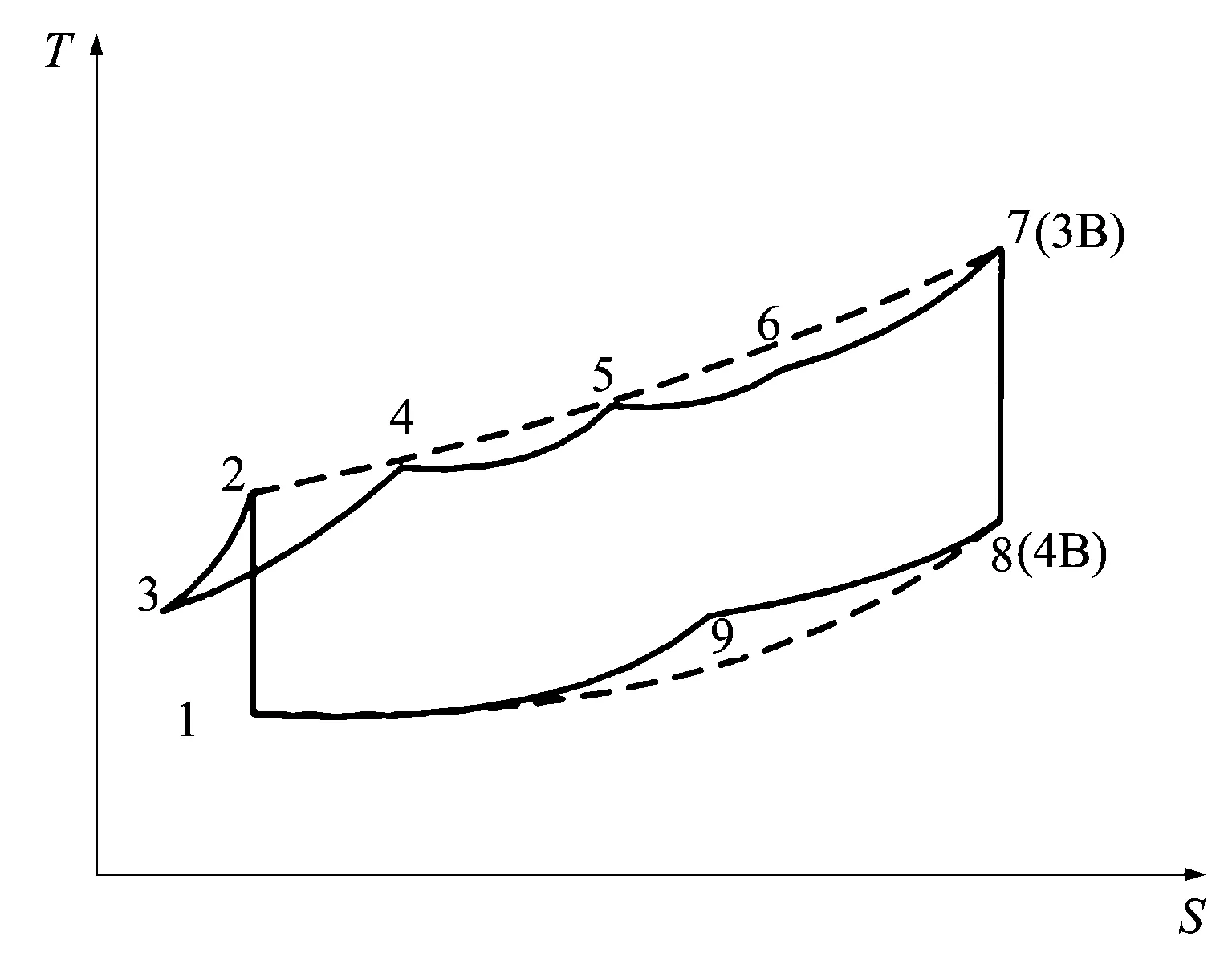
圖12 內可逆往復式M-Brayton循環與往復式Brayton循環T-s圖

類比于內可逆往復式M-Brayton循環，循環傳熱損失為

(20)

吸放熱率表示為

Qin，B=maCp(T3B-yT1)

(21)

Qout，B=maCp(T3B/y-T1)

(22)

循環功率和效率輸出為

P=Qin，B-Qout，B=
maCp[T3B(1-1/y)+T1(1-y)]

(23)

η=P/(Qin+Qleak，B)

(24)

傳熱損失產生的熵產率和工質經過功率沖程作功后由排氣沖程排往環境所產生的熵產率分別為

(25)

(26)

因此整個傳統循環的熵產率為

(27)

循環的生態學函數為

(28)

圖13為內可逆往復式M-Brayton循環和傳統往復式Brayton循環對比圖。由圖13可知：內可逆往復式M-Brayton循環的和在整個壓比范圍內要高于傳統往復式Brayton循環；當π為2～18范圍時，內可逆往復式M-Brayton循環的和高于傳統往復式Brayton循環，而當超過18時內可逆往復式M-Brayton循環的和要低于傳統往復式Brayton循環。

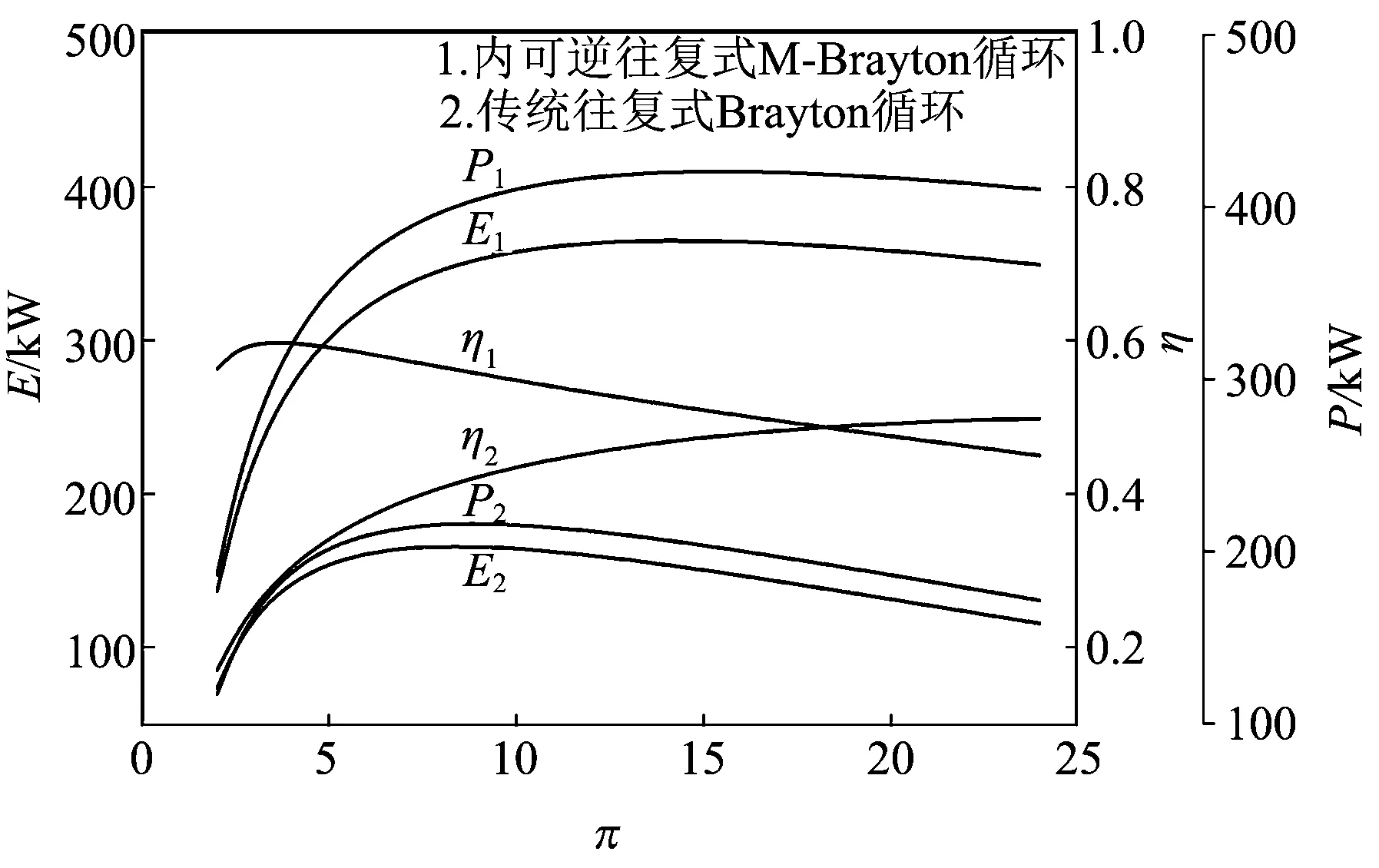
圖13 內可逆往復式M-Brayton循環與傳統往復式Brayton循環對比圖

5 結語

本文基于文獻[25]建立的考慮傳熱損失的內可逆往復式M-Brayton循環模型，進一步推導出循環熵產率、生態學函數等特性參數。由數值計算分析了3種參數對循環性能的影響，并將內可逆往復式M-Brayton循環與傳統的Brayton循環進行比較，主要結論如下。

(1)隨著T6的增加，P不改變，ηmax和Emax隨著T6的增加而增加；

(2)隨著T7的增加，Pmax、ηmax和Emax都隨之增加；

(3)隨著mwin的增加，Pmax、ηmax和Emax都隨之增加；

(4)E-P圖和E-η圖均有一段當增加到某個值就對應有兩個不同的P或η；

(5)內可逆往復式M-Brayton聯合循環在P和E上都要遠遠優于傳統Brayton循環，而僅在壓比大于18時才小于傳統Brayton循環η。