跨聲速層流翼型的混合反設計/優化設計方法

陳靜，宋文萍，朱震，許朕銘，韓忠華,*

1. 西北工業大學 航空學院 翼型葉柵空氣動力學國家級重點實驗室，西安 710072 2. 武漢第二船舶設計研究所，武漢 430064

對于現代大型客機，接近50%氣動阻力來自流動邊界層內黏性效應，而層流邊界層內黏性阻力遠小于湍流邊界層。因此，旨在保持大范圍層流邊界層的層流技術具有非常巨大的減阻潛力，被美國《航空周刊》評選成為未來20～40年內最有前景的前沿方向之一。

層流技術涵蓋自然層流技術、層流控制技術和混合層流控制技術3種。自然層流技術，作為其他層流技術的基礎，研究歷史已有80多年。2005年Honda Jet噴氣公務機[1-2]的問世，標志著自然層流技術在小型商業飛機上首次成功應用。而波音737的層流吊艙[3]以及波音787 Max的層流翼尖小翼[4]則開啟了自然層流技術在現代民用客機上局部應用的先河。

針對自然層流翼型/機翼設計，基于CFD流動的數值優化方法被廣泛應用于氣動設計中，包括反設計和直接優化設計兩種。Green[5]和Gopalarathnam[6]等均采用反設計方法開展了自然層流翼型設計工作。Campbell和Lynde[7]發展了考慮流動和幾何約束的自然層流機翼反設計方法，并初步開展了適用于大型客機的層流機翼設計工作。德國宇航院在LamAiR項目[8]中以壓力分布反設計為主要方法，設計了跨聲速自然層流前掠機翼，其上下表面均可實現大范圍層流流動。Lee和Jameson[9]進行了自然層流翼型目標壓力分布反設計，并以設計翼型為剖面配置三維機翼，進行直接減阻優化，但由于其梯度求解沒有考慮轉捩的影響，減阻效果主要來自激波的消除。Amoignon等[10]在跨聲速狀態下，將邊界層內擾動動能作為直接優化的最小化目標函數，推遲了翼型層流-湍流轉捩，但翼面激波仍較強。Zingg團隊[11-13]開展了系列單設計點和多設計點自然層流翼型直接優化設計工作。Cameron等[14]開展了基于代理模型的自然層流翼型多目標優化設計。國內對層流翼型設計也開展了大量研究，華俊等[15]采用“正反迭代、余量修正”原理進行層流翼型反設計工作；喬志德[16]采用人-機對話和壓力分布反設計的方法設計了自然層流超臨界翼型，首次提出了利用弱激波形成足夠順壓梯度的自然層流超臨界翼型設計思想。王迅等[17]利用本征正交分解(POD)代理模型實現快速轉捩判斷，并進行翼型減阻優化設計；韓忠華等[18-20]基于代理優化算法分別開展了跨聲速層流翼型和機翼減阻直接優化設計。馬曉永等[21]采用序列二次規劃優化算法開展了某民用通用飛機自然層流機翼減阻設計。同時，為了提高非設計點氣動性能，張宇飛等[22]研究了不同順壓梯度約束下優化翼型氣動特性對雷諾數等參數的敏感性，驗證了優化數學模型的選擇對于設計結果性能魯棒的重要性。高正紅等[23-25]開展了大量層流翼型減阻設計和穩健設計工作。國內還開展了大量層流翼型多目標優化設計研究[26-27]。

可見，在跨聲速層流翼型/機翼設計方面，國內外基于反設計或直接優化設計方法開展了大量研究。在反設計方法中，需預設目標流場特征(如壓力分布、擾動增長曲線等)，只有在設計領域積累了豐富經驗的專家才能根據設計指標給出合適的目標流場分布，因此，反設計方法只能局限于具有相當豐富積累的領域，而當新技術更新加速時，反設計方法很難適應于工程設計。在直接優化設計方法中，設定優化目標(如最小化阻力、最大化升阻比等)和約束，并采用數值優化算法(如遺傳算法或梯度算法等)得到優化解，該方法依賴于優化數學模型的選擇，可能會過度追求優化目標最優，而不能全面兼顧其他性能，針對該不足發展起來的多目標優化和魯棒優化設計等方法計算量巨大，很難在工程設計中實現。因此，發展能夠綜合反設計和直接優化設計方法優點而避開各自缺點的氣動優化設計新方法具有重要意義。

本文將局部反設計目標，即基于經驗/物理機理的局部目標流動分布特性，與直接優化設計目標加權組合，實現基于代理優化算法的混合反設計/優化設計方法。針對適用于現代民機的跨聲速層流機翼，采用本文發展方法開展基于代理優化算法和耦合轉捩自動判定的雷諾平均Navier-Stokes(RANS)方程求解器的跨聲速層流翼型氣動設計研究，驗證本文方法的有效性。進一步將設計翼型配置到三維機翼上，檢驗其氣動性能改進效果，并進行設計結果減阻機理分析。

1 基于混合反設計/優化設計的氣動優化設計方法

1.1 數學模型

混合反設計/優化設計方法旨在兼顧局部流場特性和總體性能指標，形成實用的設計結果。在單次優化設計過程中，既引入部分設計經驗或設計準則以指導優化設計過程，確保設計結果的實用性和魯棒性，又通過優化算法搜索設計空間，得到設計指標最優的氣動外形。本文中，反設計問題和直接優化問題被分別表達為單目標優化問題，并通過權重系數組合成多目標優化問題，其數學模型表示為

min obj=w1objinv+w2objdir

w.r.t.x∈(xl,xu)

(1)

式中：objinv表示反設計目標函數，objdir表示直接優化設計目標函數，通過權重系數w1、w2組合成混合反設計/優化設計總目標obj；hp為氣動或幾何相關等式約束；Np為等式約束數目；gm為氣動或幾何相關不等式約束；Nm為不等式約束數目；設計變量為x序列，xl和xu分別為設計變量的變化上下邊界。

當w1=1、w2=0時，該模型為直接優化形式下的反設計問題；當w1=0、w2=1時，該模型為直接優化設計問題；當w1、w2在0～1之間時，該數學模型為綜合直接優化設計和反設計的混合反設計/優化設計問題。針對不同的氣動優化問題，反設計目標objinv是根據設計經驗或物理背景等確定的流場特性分布函數，如局部壓力分布、載荷分布或某種氣動設計準則等，而直接優化設計目標objdir通常為升阻特性或其他有待改善的性能指標。通過將混合反設計/優化設計問題構造為上述多目標優化問題，確保優化外形具備目標流場特征，且性能指標得到優化。

1.2 幾何參數化及設計空間選擇

采用基于型函數/類函數變換的參數化方法(CST)描述翼型幾何形狀。該方法最早由Kulfan[28]提出，表達式為

(2)

(3)

采用擾動CST方法得到描述翼型的設計參數后，還需確定各參數在優化設計中的取值范圍，從而確定設計空間大小。在優化前并不知道最優外形所在設計空間，因此，先以基準翼型為設計空間中心，給定設計參數范圍，如果優化翼型設計參數達到上下邊界，則將優化翼型作為新的設計空間中心，開展新一輪優化設計，直到優化翼型設計參數全部被包含在設計空間內。

1.3 代理優化設計

代理優化算法作為一種新型的高效優化設計方法，在航空航天界受到了重視，并快速發展起來。該方法通過建立一種計算量小的近似數學模型“代替”原有的高精度數值模擬，大幅降低計算量和計算時間，實現高效的數值優化。本文在代理優化器“SurroOpt”[30-32]基礎上，實現了基于混合反設計/優化設計方法的氣動優化設計框架，如圖1所示，具體步驟如下：

圖1 代理優化設計方法流程圖Fig.1 Flow chart of surrogate optimization design method

步驟1采用試驗設計方法(DoE，如拉丁超立方等)在給定設計空間內隨機抽樣產生初始樣本點。

步驟2調用CFD分析程序，計算混合反設計/優化設計目標函數值及約束函數值。

步驟3基于已有樣本數據分別建立目標函數和約束函數的代理模型(如Kriging等)。

步驟4采用不同的自適應加點技術(如Expected Improvement(EI)、Minimizing Surrogate Prediction(MSP)、Probability of Improvement(PI)、Lower Confidence Bound(LCB)等)在代理模型上進行子優化，增加新樣本點。

步驟5調用CFD分析程序，計算新增樣本點混合反設計/優化設計目標函數值及約束值，更新代理模型，重復步驟4和步驟5，直到優化過程終止于優化收斂準則。

2 流動數值模擬方法及驗證

2.1 耦合轉捩自動判定的RANS流場求解器

采用耦合轉捩自動判定的RANS流場求解器(PMNS2D/3D)[33-34]開展翼型/機翼繞流數值模擬計算。RANS求解器與轉捩預測模塊的耦合框架如圖2所示。RANS主流場求解模塊采用S-A(Spalart-Allmaras)湍流模型,中心格式空間離散，LU-SGS(Lower-Upper Symmeffic Gauss-Seidel)隱式時間推進；轉捩預測模塊包括可提供高精度邊界層信息的層流邊界層求解和基于線性穩定性理論的eN方法兩部分。在eN方法中，擾動放大因子增長到預設閾值時，判定層流-湍流轉捩發生。

圖2 RANS求解器與轉捩模塊耦合策略示意圖Fig.2 Coupling scheme of RANS solver and transition module

2.2 流場求解器驗證

2.2.1 NLF(1)-0416翼型繞流自由轉捩計算

對NLF(1)-0416翼型開展考慮轉捩影響的數值模擬計算。在計算狀態馬赫數Ma=0.3,雷諾數Re=4×106,迎角α=2.03°下，層流邊界層內位移厚度計算值與文獻[9]吻合較好，如圖3所示，驗證了求解器中邊界層求解程序的可靠性。在計算狀態Ma=0.1,Re=4×106下，采用eN方法對NLF(1)-0416翼型邊界層進行轉捩判斷。對于半經驗的eN方法，航空界經過大量研究，綜合考慮影響轉捩的各種因素，將轉捩放大因子閥值(NTS)tr取為9，作為設計參考值。然而在具體風洞試驗中，試驗條件、模型加工精度等差異會導致不同試驗標定得到的轉捩放大因子取值存在差異。本驗證算例中(NTS)tr=11，參考德國宇航院對該試驗數據的標定結果[35]。轉捩放大因子(NTS)tr=9，11時，NLF(1)-0416翼型0°迎角下壓力分布與轉捩位置Xtr對比見圖4，可見兩個不同轉捩放大因子值計算得到的壓力系數Cp分布和所預測的轉捩位置差異不大。

圖5是上表面Tollmien-Schlichting (TS)波擾動NTS增長曲線，可以看出TS波擾動因子(NTS)tr增長劇烈，曲線陡峭。針對此特點，(NTS)tr在合理范圍內取值時，不會對TS波誘導轉捩位置有較大影響。不同迎角下，翼型上表面轉捩位置預測值與試驗結果的對比如圖6所示。可見(NTS)tr=9，11時，所預測的轉捩位置差異不大，均基本在試驗值合理范圍內。根據參考文獻標定取11時，計算結果更接近試驗值，表明本文轉捩判定方法能準確預測翼型表面層流-湍流轉捩。

圖3 NLF(1)-0416翼型上表面位移厚度δ*比較Fig.3 Comparison of displacement thickness δ* for NLF(1)-0416 airfoil upper surface

圖4 NLF(1)-0416翼型壓力分布和轉捩位置比較Fig.4 Comparison of pressure distribution and transition locations on NLF(1)-0416 airfoil

圖5 NLF(1)-0416翼型上表面TS波擾動增長曲線Fig.5 Disturbance growth curves of TS wave on NLF(1)-0416 airfoil upper surface

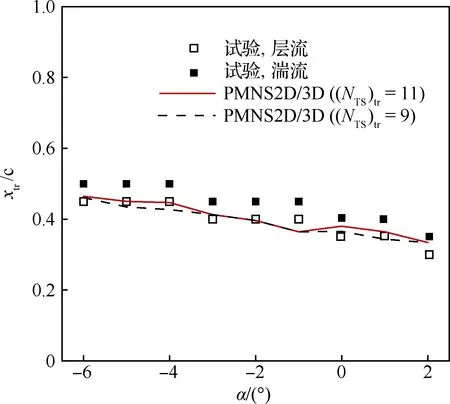
圖6 NLF(1)-0416翼型上表面轉捩位置與試驗結果比較Fig.6 Comparison of transition locations on NLF(1)-0416 airfoil upper surface with experiment results

2.2.2 NPU-LSC-72613翼型跨聲速繞流自由轉捩計算

本節對NPU-LSC-72613[36]翼型開展考慮轉捩影響的數值模擬計算，驗證跨聲速流動狀態下本文使用的轉捩預測技術的可靠性。由于現有公開資料中，沒有帶自然轉捩的跨聲速翼型試驗數據,因此本文通過與MSES軟件結果對比來驗證跨聲速狀態下轉捩判斷的可靠性。MSES是一款由美國Drela教授開發，業界公認較為成熟的軟件，通過求解Euler方程耦合eN轉捩判斷方法進行翼型繞流模擬及轉捩判斷。計算狀態Ma=0.72，Re=2.0×107，升力系數CL=0.6。圖7是本文方法計算得到的壓力分布及上下表面轉捩位置與MSES軟件結果的對比，壓力分布和上下表面轉捩位置吻合較好，驗證了本文方法在跨聲速流動狀態下對翼型邊界層轉捩預測的可靠性。

圖7 NPU-LSC-72613翼型壓力分布和轉捩位置比較Fig.7 Comparison of pressure distribution and transition locations on NPU-LSC-72613 airfoil

2.2.3 無限展長后掠機翼NACA642A015繞流自由轉捩計算

以NACA642A015翼型為橫剖面的后掠機翼在美國Ames 12英尺的低湍流度風洞進行了試驗[37]。對于后掠角40°機翼，采用雙eN方法[38]判斷轉捩，對于風洞試驗中無限翼展后掠機翼邊界層轉捩，本文參考文獻[38]中標定結果，TS波和CF波轉捩擾動放大因子閥值取[NTS,NCF]tr=[10.5,7.5]。圖8給出了Ma=0.27,Re=5.7×106，α=-1.5°狀態下，計算壓力分布與試驗值對比。圖9展示了不同雷諾數下，機翼上表面計算轉捩位置與試驗值比較，可見，計算值與試驗值吻合較好。

本文采用的機翼轉捩判斷方法為雙eN方法，在判斷轉捩位置的同時可以判定轉捩是由CF波不穩定性導致還是TS波不穩定性導致。圖10給出NACA642A015后掠機翼上表面TS波和CF波擾動因子N增長曲線，從圖中可以看出CF波擾動增長曲線先于TS波達到對應閥值，邊界層轉捩由CF波增長導致。對于40°后掠機翼，由CF波不穩定性導致轉捩是合理的，轉捩位置與試驗值也吻合較好，驗證了本文RANS求解方法在三維機翼上轉捩預測的可靠性。

圖8 NACA642A015后掠機翼壓力分布Fig.8 Pressure distribution on NACA642A015 swept wing

圖9 NACA642A015后掠機翼上表面轉捩位置Fig.9 Transition locations on NACA642A015 swept wing upper surface

圖10 NACA642A015后掠機翼上表面TS波和 CF波擾動增長曲線Fig.10 Disturbance growth curves of TS and CF wave on NACA642A015 swept wing upper surface

3 方法驗證

3.1 跨聲速自然層流翼型優化設計

針對適用于現代中短程民機的跨聲速層流機翼設計要求，開展主翼型氣動設計研究。機翼巡航狀態為Ma=0.75，Re=2.0×107，CL=0.5，則主翼型設計狀態為Ma=0.729，Re=2.0×107，CL=0.556，轉捩放大因子閥值取(NTS)tr=9。本節選取翼型NPU-LSC-72613為基準外形。

跨聲速層流翼型氣動設計要求兼顧優良的超臨界特性和自然層流特性。在跨聲速狀態下，前者要求翼型表面激波盡可能弱，以減小激波引起的壓差阻力；后者則要求翼面保持穩定的順壓梯度，以抑制邊界層內不穩定擾動波劇烈增長，保持大范圍的自然層流流動。

綜合上述氣動設計準則，設計了具有穩定、較小順壓梯度的翼型上表面局部壓力分布，作為混合反設計/優化設計方法中的反設計目標壓力分布，如圖11 所示。同時，將翼型總阻力CD作為混合反設計/優化設計方法中的直接優化設計目標。

優化過程中，采用8階擾動CST參數化方法，設計變量18個，氣動約束為：① 保持升力系數CL不小于基準外形；② 力矩系數Cm不小于基準外形；幾何約束為翼型相對厚度t/c不減；優化數學模型如式(4)所示。優化前后翼型氣動性能計算采用C型結構化網格，如圖12 所示。

min obj=w1objinv+w2objdir=

w.r.t.x∈(-0.02,0.02)

s.t.CL≥0.556;Cm≥-0.139;t/c≥12.7%

(4)

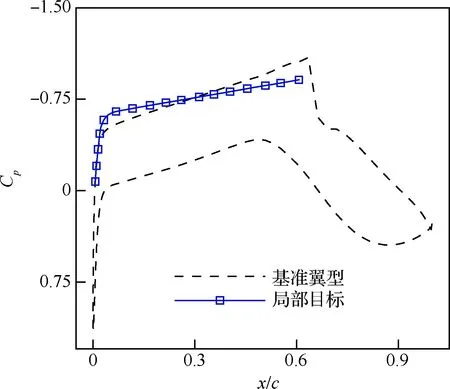
圖11 局部目標壓力分布與基準翼型壓力分布Fig.11 Distributions of pressure of local target and baseline airfoil

圖12 C型結構化計算網格(641×241)Fig.12 C type structured computation grid (641×241)

3.2 混合反設計/優化設計

本算例優化設計進行了兩輪，第1輪設計中，以基準翼型為設計空間中心，權重系數w1、w2分別取0.3和0.7，經過200次CFD計算后，混合反設計/優化設計過程收斂，收斂歷程曲線如圖13所示。可見，優化設計目標經歷了一次顯著下降，且反設計和直接優化設計目標均為下降趨勢，隨后目標函數值沒有進一步下降。圖14 給出了當前最優設計點的壓力分布曲線，及其與局部目標壓力分布和基準翼型壓力分布的比較。相比于基準翼型，當前最優設計的吸力面激波減弱，局部壓力分布更接近目標分布，但仍然存在明顯差別，需要進一步提高反設計部分的優化效果。經校驗，當前最優點處設計變量值有77.8%達到給定設計空間邊界，說明設計空間外可能存在更優的氣動外形，需調整當前設計空間。

圖13 第1輪混合反設計/優化設計收斂歷程Fig.13 Convergence history of first round hybrid inverse/direct optimization design

圖14 第1輪設計優化翼型、基準翼型和 局部目標壓力分布Fig.14 Pressure distributions of optimal airfoil, baseline airfoil, and local target of first round design

通過將第1輪設計最優點作為擾動中心，改變設計空間，開始第2輪混合反設計/優化設計過程。同時根據第1輪優化結果分析，權重系數w1、w2調整為0.11和0.89。圖15 給出了第2輪設計過程的優化收斂歷程，可見，直接優化設計目標先是小幅上升后又小幅降低，反設計目標有多次顯著下降。

經過2輪混合反設計/優化設計后，圖16給出了優化翼型壓力分布，及其與局部目標壓力分布和基準翼型壓力分布的比較。可見，優化翼型的吸力面局部壓力分布與目標壓力分布吻合很好，反設計效果顯著，而與基準翼型相比，優化翼型吸力面順壓力梯度減弱，激波位置不變，但強度減弱，有利于總阻力降低。圖17給出了優化前后翼型幾何形狀比較，優化翼型前緣半徑增大，吸力面前緣加速更快，而相對厚度基本保持不變。圖18 給出了翼型優化前后，馬赫數在流場中的分布云圖對比，優化翼型保持了大范圍的超聲速區，但激波前馬赫數小于基準翼型，激波強度減弱。

圖15 第2輪混合反設計/優化設計收斂歷程Fig.15 Convergence history of second round hybrid inverse/direct optimization design

圖16 第2輪設計優化翼型、基準翼型及 局部目標壓力分布Fig.16 Pressure distributions of optimum airfoil, baseline airfoil and local target of second round design

圖17 優化翼型與基準翼型幾何形狀對比Fig.17 Comparison of geometry of optimum airfoil and baseline airfoil

圖18 優化翼型和基準翼型馬赫數云圖Fig.18 Mach number contours of optimum and baseline airfoils

表1給出了優化前后翼型氣動性能的比較，可見優化翼型升力系數、力矩系數和相對厚度嚴格滿足約束，優化翼型總阻力CD下降6 counts(1 count=0.000 1)， 約占基準翼型阻力的15.5%。 從表中給出優化前后翼型阻力分解值及轉捩位置可見，優化翼型激波阻力CDw降低了5.4 counts， 黏性阻力CDv降低了0.6 count，且上下表面轉捩位置(Trans_x)均在55%倍弦長之后。結果表明，經過2輪混合反設計/優化設計，翼型激波強度顯著降低，具有較好的超臨界特性，并保持了優良的自然層流特性，說明混合反設計/優化設計方法效果顯著。

表1 優化翼型與基準翼型氣動性能比較Table 1 Comparison of aerodynamic performances ofoptimum airfoil and baseline airfoil

4 配置基準翼型和優化翼型的跨聲速自然層流機翼氣動性能對比

為驗證所設計翼型對跨聲速自然層流機翼性能提升的效果，針對平面幾何形狀如圖19所示的跨聲速層流機翼進行了氣動性能對比計算。機翼翼根扭轉角為0°，翼尖扭轉角為-2°。沿順氣流方向分別配置優化翼型和基準翼型，得到設計機翼和初始機翼。巡航狀態Ma=0.75，Re=2.0×107，CL=0.5，對兩機翼開展考慮自由轉捩的繞流數值模擬計算。本文設計的算例主要針對于民用客機，其飛行高度在萬米左右，大氣環境十分安靜，擾動較小，擾動放大因子臨界值相對于低空環境偏高。在歐洲大量飛行試驗[39]基礎上，對試驗對象進行穩定性分析及擾動放大因子臨界值進行標定，得出了在實際飛行狀態(區別于實驗室環境)中，層流-湍流轉捩的擾動放大因子臨界值[NTS,NCF]tr=[10.5,10]，具有參考意義。在優化設計時，為了能夠設計出對環境擾動更加魯棒的氣動外形，本文選擇擾動放大因子臨界值時乘以相應的安全系數，轉捩擾動因子閥值取[NTS,NCF]tr=[9,8.5]。取值更低的閥值可以保證設計外形更加魯棒，在來流湍流度擾動時，機翼表面始終能夠獲得足夠的層流范圍。計算網格為C-H 型結構化網格，如圖20所示。

圖19 跨聲速層流機翼平面形狀Fig.19 Planform of transonic laminar flow wing

圖20 機翼繞流計算C-H型結構化網格(257×105×73)Fig.20 C-H type structured computation grid for wing flow calculation (257×105×73)

表2給出了設計機翼與初始機翼氣動性能比較，相比于初始機翼，設計機翼阻力系數下降8 counts。力矩參考點在平均氣動弦的25%弦長處，力矩系數絕對值較小，升阻比由38.88提高到41.46，提升了約6.64%。機翼優化效果沒有表1中翼型優化氣動性能的提升明顯，下面進行詳細分析。從阻力組成上看，二維翼型阻力包括黏性壓差阻力、激波阻力和摩擦阻力3種；三維機翼阻力則包括誘導阻力、黏性壓差阻力、激波阻力和摩擦阻力4種。二維翼型相較于三維機翼，其激波阻力在總阻力中占比更高。本文優化目標是保持大范圍層流的基礎上，減弱激波，減少總阻力。從優化結果看，優化翼型激波明顯減弱，而層流流動保持很好，并沒有發生較大變化，總阻力降低的主要貢獻來自激波阻力的下降。在三維機翼中，通過比較優化機翼自然轉捩和固定轉捩計算結果，可知機翼阻力下降仍然主要源于激波減弱，但由于激波阻力在總阻力中占比不高，減阻百分比稍低。

同時，該現象也表明為了更好地優化機翼，應該考慮下一步將混合反設計/優化設計方法直接應用于三維機翼，在設定局部流動特征約束時，綜合考慮激波阻力、黏性阻力和誘導阻力，達到總體最優效果。

圖21展示了設計機翼和初始機翼上翼面壓力分布云圖和上下翼面轉捩線。相比于初始機翼，設計機翼上表面順壓梯度減小，激波強度減弱，但仍然保持了大范圍層流流動；設計機翼下表面將翼根部分轉捩位置從前緣推遲到40%弦長之后，層流范圍明顯增大。基準機翼翼根下表面邊界層由于橫流不穩定導致前緣轉捩，而優化機翼此處橫流不穩定得到抑制，從而推遲了轉捩的發生。

表2 設計機翼與初始機翼氣動性能比較Table 2 Comparison of aerodynamic characteristics ofdesigned and baseline wing

順壓梯度不利于抑制橫流CF不穩定波的發展，而機翼前緣存在劇烈加速區，是CF波誘導前緣轉捩的“高危區”。比較圖22翼根下表面壓力分布可以看出，優化機翼下表面前緣加速區更短，有利于穩定橫流CF波擾動因子在機翼前緣的劇烈增長，從而推遲轉捩發生。圖23給出的是初始機翼和設計機翼下表面翼根處TS波和CF波擾動增長曲線，可以看出轉捩由CF波不穩定誘導，設計機翼主要是抑制了CF波不穩定性推遲了轉捩。為了進一步分析初始機翼與設計機翼下表面翼根前緣區域橫流強度對比，圖24給出了8.4%展向位置前緣加速區4個流向站位上邊界層內無量綱化的橫流速度型的對比，圖中縱坐標Y為距物面無量綱高度，橫坐標W為無量綱橫流速度。橫流速度型拐點速度越大，拐點與物面距離越小，則橫流強度越大，對應的CF波不穩定擾動放大率越大。從圖24中可見，在前緣加速區，隨流向速度的增大，4個流向站位處的無量綱橫流強度W沿流向遞減。同時，設計機翼每個流向站位處的橫流強度相對初始機翼有所減弱。

圖25給出了一定升力系數范圍內，設計機翼和初始機翼升阻極曲線、力矩系數和升阻比隨升力系數的變化曲線，可見，設計機翼氣動性能在一定升力系數范圍內均有顯著提高，驗證了優化翼型優良的超臨界特性和自然層流特性，說明了在跨聲速自然層流翼型設計中混合反設計/優化設計方法的有效性。需要說明的是，本文考慮的機翼設計狀態(CL=0.5)的升阻比不在單獨機翼的最大升阻比位置，是因為當考慮機身阻力后，翼身組合體的最大升阻比在CL=0.5左右。

圖21 設計機翼和初始機翼上翼面壓力分布云圖及上下翼面轉捩線比較Fig.21 Comparisons of pressure contours of upper surface and transition lines on designed and baseline wings

圖22 初始機翼和設計機翼翼根站位壓力分布比較Fig.22 Comparison of pressure coefficients at wing root station of baseline wing and designed wing

圖23 初始機翼與設計機翼在翼根站位下表面TS波和 CF波擾動增長曲線Fig.23 Disturbance growth curves of TS and CF wave on lower surfaces at wing root station of baseline wing and designed wing

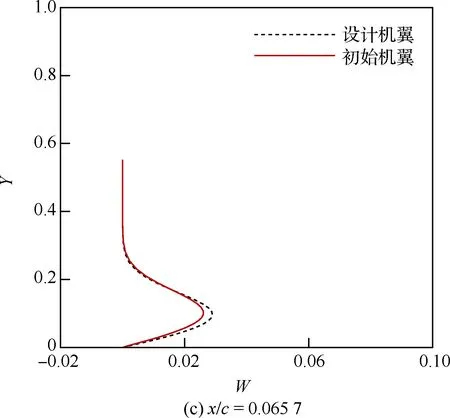
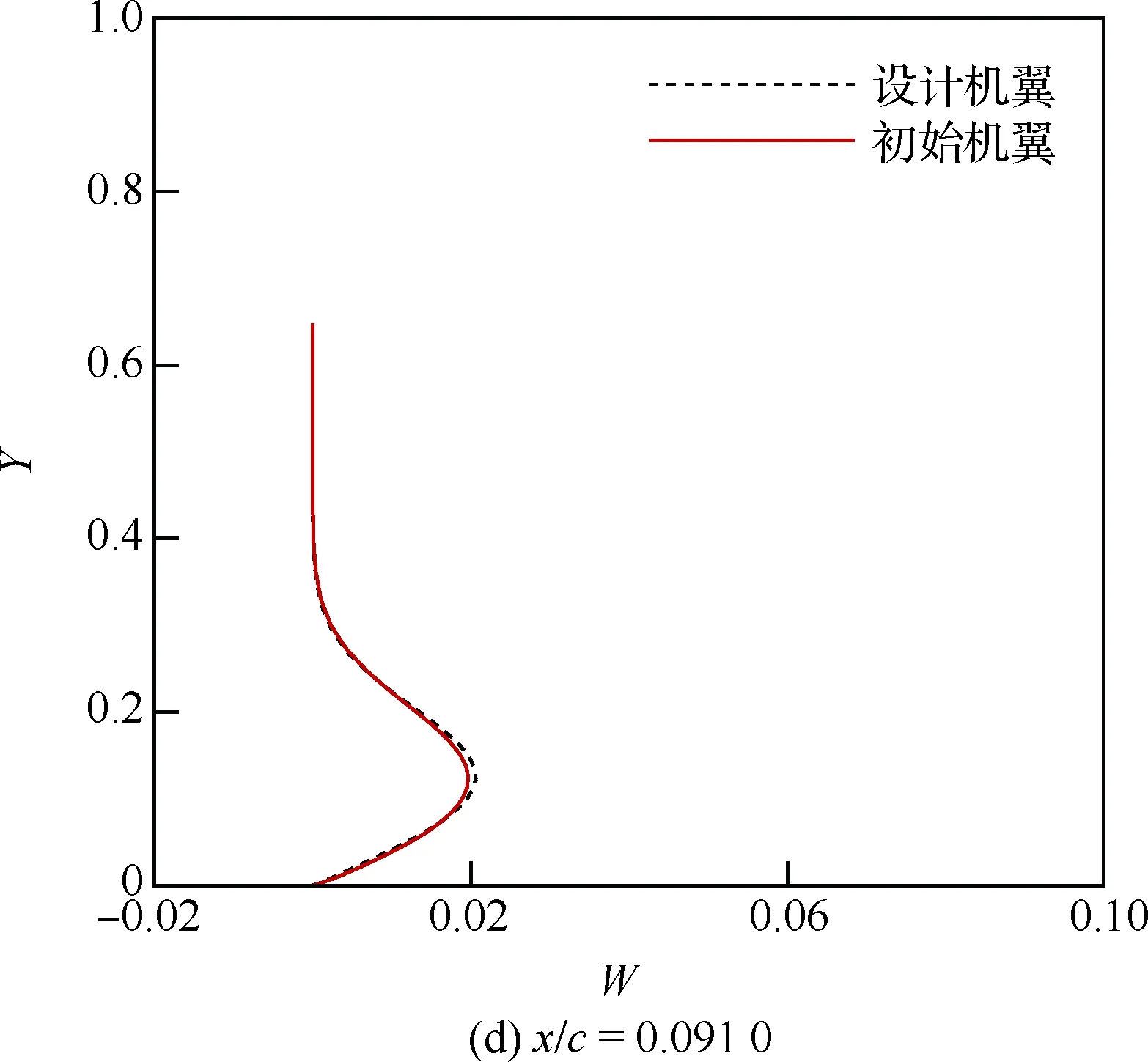
圖24 初始機翼和優化機翼翼根站位下 表面邊界層內橫流速度型比較Fig.24 Comparisons of cross flow profiles inside boundary-layers on lower surfaces at wing root station of baseline wing and designed wing

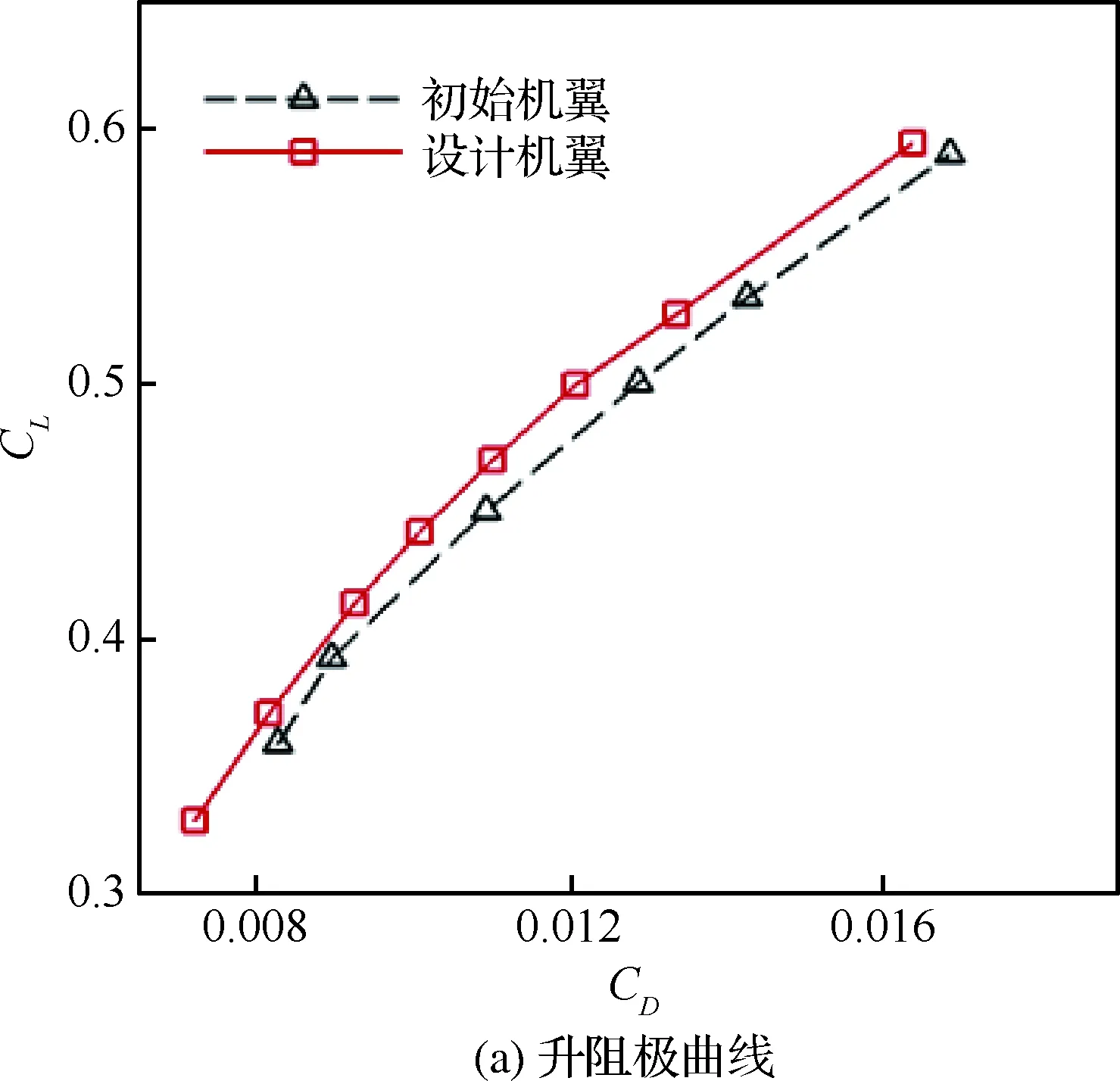
圖25 設計機翼和初始機翼氣動性能曲線Fig.25 Aerodynamic performance curves of designed and baseline wings

5 結論與展望

1) 在基于代理模型的通用優化框架下，實現了混合反設計/優化設計方法。將反設計目標函數與直接優化目標函數通過權重系數組合，構造了多目標優化形式下的混合反設計/優化設計問題，以實現局部流場特性反設計及總體性能指標優化。

2) 將混合反設計/優化設計方法成功應用于跨聲速自然層流翼型設計研究。與基準翼型相比，優化翼型實現目標局部壓力分布，總阻力下降15.5%，激波強度減弱，保持了大范圍層流，具有良好的超臨界和層流特性，其優良氣動特性在三維機翼上也得到驗證，說明了混合反設計/優化設計方法處理跨聲速層流翼型設計問題的有效性。

3) 用多輪優化策略應對優化設計空間選擇問題。第1輪優化設計中，在給定設計空間尋找最優解，如果優化結果在當前設計空間邊界，則以當前最優解為中心，定義新的設計空間，開展新一輪優化設計，以避免初始設計空間可能不包含最優解的問題。

下一步擬將混合反設計/優化設計方法直接應用于三維機翼，在設定局部流動特征約束時，綜合考慮跨聲速層流機翼的激波阻力、黏性阻力和誘導阻力，達到總體最優效果。