結冰飛機著陸階段飛行安全包線確定及操縱應對策略

周馳，李穎暉，鄭無計，武朋瑋，董澤洪

空軍工程大學 航空工程學院，西安 710038

近年來由結冰所導致的飛行事故持續發生，結冰不僅會破壞飛機的動力學特性，同時也會對駕駛員的操縱造成嚴重影響。在未察覺結冰的情況下，飛行員的操縱極易使飛行狀態超出飛行安全包線，最終引發飛行事故[1]。美國國家航空航天局(NASA)及聯邦航空管理局(FAA)統計的1976—1994年間所發生的飛行事故，有16起與飛機結冰有關，并導致了139人死亡[2]。美國Safety Advisor[3]對1990—2000年間因氣象原因造成的飛行事故進行了統計，其中結冰事故就占了12%。飛機遭受結冰影響，不僅升力減小，阻力增大，同時失速迎角也會相應減小，此時飛控系統可能會給機組提供一個錯誤的操縱指導，從而給飛行安全造成重大隱患，因此飛行包線確定對于提升飛行安全具有重要意義。傳統的安全包線通常是在飛機的歐拉角、負載、飛行速度等飛行參量上加以限制，并認為只要不超出這些限制，飛機就能安全飛行[4]。但在環境因素(結冰、強風)等影響下，傳統的安全包線就不再適用。1994年，美國鷹航公司的一架ATR72-212飛機墜毀于印第安納Roselawn地區，當時飛機的飛行迎角僅為5°，這遠低于飛控系統提供的迎角限制值18.1°，可是在機翼重度結冰的影響下，飛機仍然因失速而導致事故發生[5]。

為了保障飛行安全，必須建立能夠考慮多種外在因素影響的飛行安全包線。近年來，國內外對于安全包線的確定方法進行了較為廣泛的研究，其中ROA(Region Of Attraction)方法[6-7]被用于安全包線的確定，但是ROA方法主要是基于Lyapunov能量函數[8]確定包線，函數的確定方法本身存在較強的保守性。Zheng等[9]提出了基于流形理論將飛行系統在特定飛行狀態下的穩定域作為飛行安全包線，該方法雖然得到了較為精確的飛行系統的安全包線，但該方法主要是基于飛機的動力學特性確定包線，對模型的精度要求較高，因此也很難被工程應用。國內外在對于可達集方法確定安全包線上也進行了大量研究[10-13]，其中可達集的確定主要基于Mitchell的水平集工具箱[14]。但這些研究大多只是確定了飛行器完成機動動作的安全包線，并沒有在操縱策略上有具體的研究，特別是對于著陸階段的研究較少。

結冰會導致飛行安全包線收縮雖然已是業界共識，但國內外對如何確定結冰時安全包線的研究較少且局限性較大[15-17]。本文基于可達集理論，提出了將正向可達集與反向可達集的交集作為安全集，即飛行安全包線，并將其應用于結冰飛機著陸階段。可達集的確定是基于水平集方法計算Hamilton-Jacobi方程的最優解，具體求最優解的過程采用了最優控制的方法。其中反向可達集的計算是在最優控制作用下從選定的初始集出發，計算能到達目標集的集合。另外飛機著陸時其飛行狀態不可能一直能保證從初始狀態開始按照預定軌道到達目標集，當遇到突發狀況時，可以通過從初始狀態出發計算正向可達集，這樣又能重新找到新的安全初始狀態。在著陸階段，安全的著陸過程也被定義為能從初始狀態安全到達指定目標狀態的過程，飛行安全包線作為正向可達集和反向可達集的交集，只要使飛行狀態永遠保持在安全包線以內，就能保證飛機安全著陸。本文以NASA的項目飛機GTM(Generic Transport Model))作為背景飛機，通過對飛機的氣動參數進行多項式擬合，建立了結冰飛機縱向通道的動力學模型。然后分別對輕度結冰和重度結冰飛機的安全包線進行了確定。最后以安全包線作為飛行安全的評價標準，對具體的飛機著陸過程進行了試驗仿真驗證，并提出了相應的操縱策略。

1 結冰飛機非線性模型建立

結冰會破壞飛機的動力學特性，導致升力減小、阻力增大，同時失速迎角也會大幅減小，如圖1 所示，圖中：CL為升力系數，α為迎角。因此飛行安全包線也會發生明顯變化，為了確定結冰后的安全包線，首先應該建立結冰飛機的動力學模型。

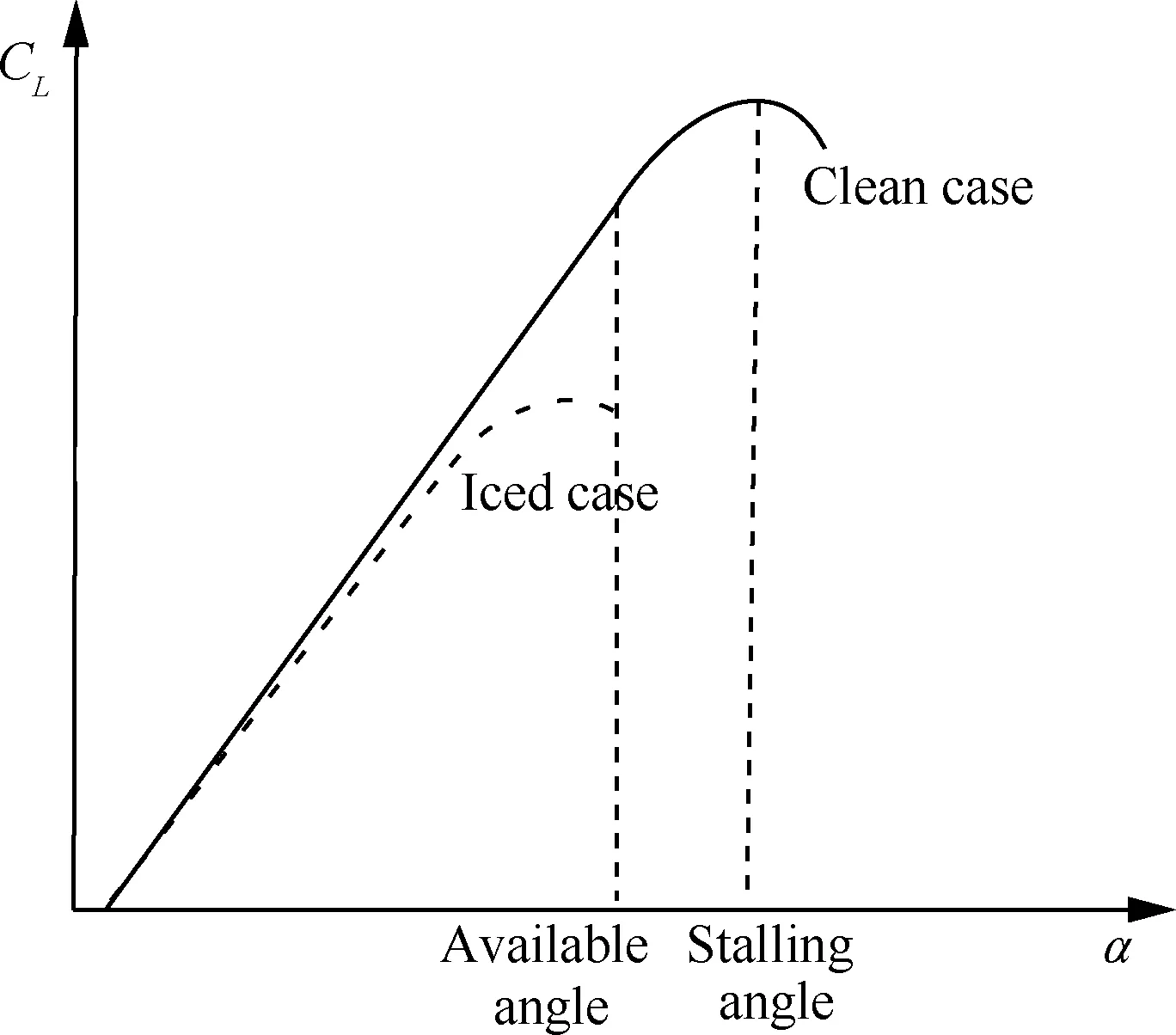
圖1 結冰前后升力系數變化示意圖Fig.1 Sketch map of variation of lift coefficient of aircraft before and after icing

結冰飛機著陸階段飛行安全包線變化的過程中，通常飛機剛體模型主要包含6個自由度，但飛機在著陸階段主要是針對縱向通道進行控制，因此本文不考慮飛機橫側向通道的狀態參數變化；另外本文所涉及的控制是對飛行系統進行外環控制，不考慮飛機系統內環控制的影響，因此假定駕駛員的操縱將直接改變迎角，不考慮飛機自身的轉動特性[11,18]。本文研究的模型簡化為如下形式。

1.1 縱向通道飛機動力學模型建立

本文采用的結冰飛機非線性動力學方程為

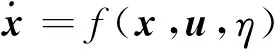
(1)

式中:狀態變量x中包含飛行速度V，航跡傾角γ和高度H；控制量u由推力T和迎角α組成；η作為結冰因子表示飛機的結冰程度。建立的飛機三維非線性動力學模型表示為

(2)

式中:m為飛機質量;L為升力;D為阻力。升力和阻力可以表示為

(3)

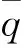
1.2 結冰飛機多項式系數模型建立

通過對飛行數據進行參數擬合[20]能夠得到氣動數據隨迎角α、俯仰角速度q以及升降舵偏角δe變化的精確的多項式形式的解析表達式，具體表達式為

(4)

式中：多項式系數xi(i=1,2,3,4)和zi(i=1,2,3,4)是結冰因子η的函數，文獻[1]指出，可通過式(5)體現結冰程度對飛機氣動特性的影響。

C(A)iced=(1+ηKC(A))C(A)

(5)

式中：KC(A)用于表示結冰后飛行參數的變化，對于特定的飛機通常為常數；C(A)為結冰前力或力矩系數。結冰因子η作為一個時變量，隨著結冰程度的加劇，從0到ηmax變化。其中η=0表示飛機無結冰，η=ηmax表示飛機已經完全結冰。

2 安全包線確定

飛行安全包線對于保障飛行安全尤為重要，傳統的包線主要是對飛行姿態加以限制，并認為只要不超過限制就能確保安全。但是傳統方法卻不適用于因環境因素引起的變化，特別是結冰導致的飛機機體結構變化，而基于可達集理論確定的飛行安全包線能夠解決這一問題。下面針對可達集理論計算安全包線進行具體介紹。

2.1 安全集定義

可達集的概念可表示為從初始集出發在某個控制作用下在一定時間內到達目標集的過程。對于飛機著陸來說就是在飛控系統或駕駛員作用下從著陸的初始狀態到達預定的目標狀態的過程。在數學上飛機的動態特性可以表示為

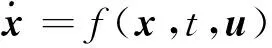
(6)

式中：x∈Rn為n維狀態空間;t為時間；u∈U為控制量。其中f:Rn×[0,T]×U→Rn有界且為Lipschitz連續。狀態軌跡可以定義為ξx0,t0,u(·)(t):t→x∈Rn，其中x0代表在時間t=t0時的狀態，u(·)為此時的控制輸入。初始集和目標集分別表示為I,Γ∈Rn。

正向可達集可定義為在時間t0從初始集出發在時間t處到達的狀態集合，而反向可達集定義為從時間t出發在時間tf時到達目標集的狀態集合，數學表達式為

正向可達集：

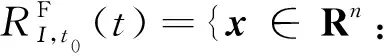
[Ι,U]|ξx0,t0,u(·)(t)=x}

反向可達集：

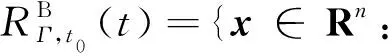
本文的研究主要是為了確保結冰飛機能在控制作用下安全著陸，反向可達集雖然理論上總能保證飛機在一定時間內通過某個控制從初始集到達目標集，但是其中的某些狀態點可能會超出飛機本身的限制(如飛行速度低于失速速度，迎角大于失速迎角等)。特別是對于著陸階段，飛行狀態不可能一直保證從初始狀態開始按照預定軌道到達目標集，飛機為了便于進行狀態切換，必須不斷地尋找新的狀態點，甚至反向尋找新的合適的初始狀態，這樣就需要計算正向可達集。因此本文將正向可達集與反向可達集的交集作為安全集，安全集也定義為飛行安全包線，在安全包線內飛機能夠通過可達集算法中的最優控制方法進行任意的狀態切換，從而實現飛機的安全著陸。安全集如圖2所示。圖中綠色部分為正向可達集，紅色部分為反向可達集，黃色部分為初始集，而安全集為綠色與紅色相交部分。

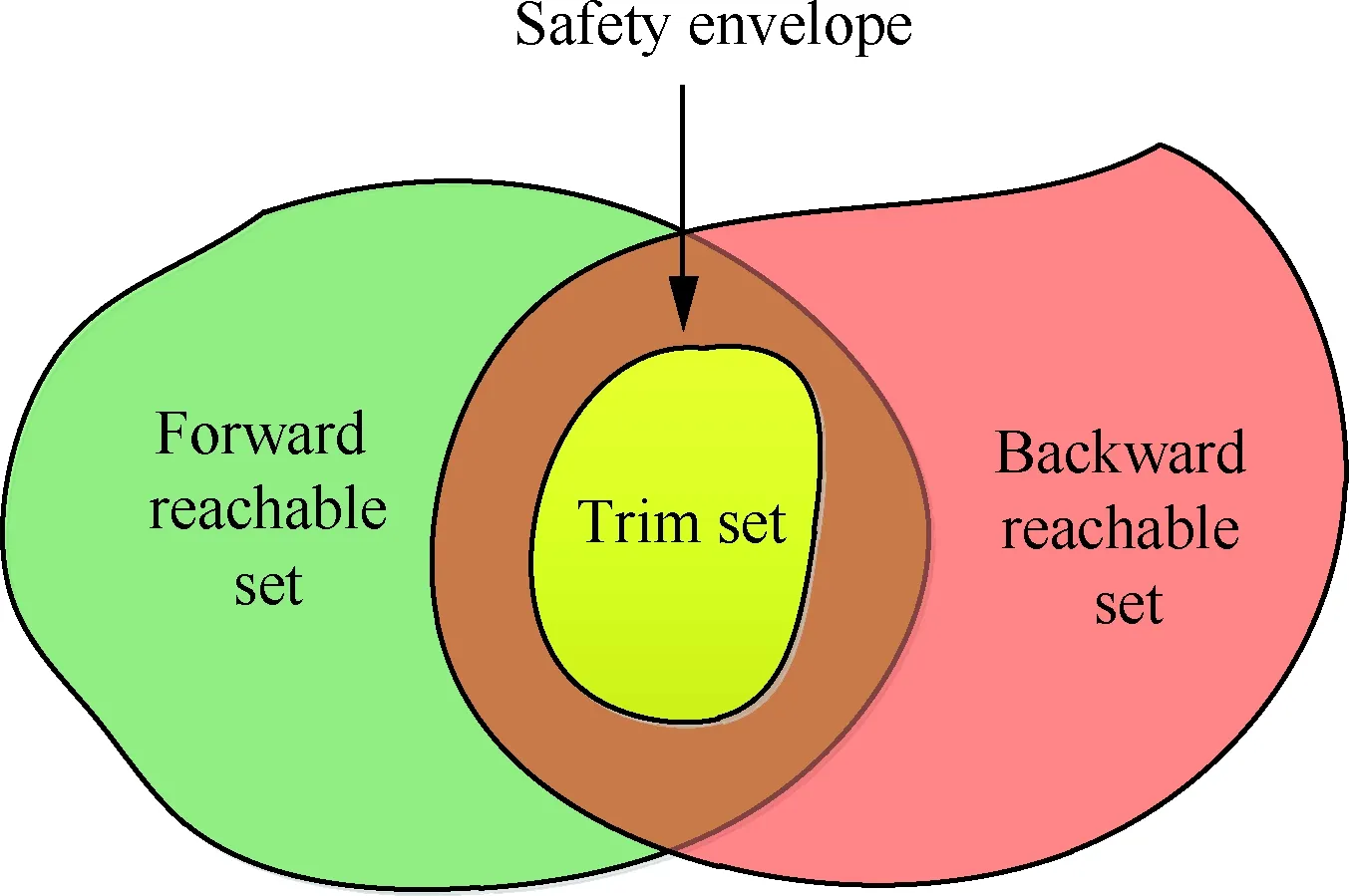
圖2 安全集示意圖Fig.2 Sketch map of safety sets

2.2 水平集方法

目標集和可達集都可由水平集方法表示，水平集方法是一種用于跟蹤界面移動，計算隱式曲面演變的數值方法[21]。其基本思想是把低維動態曲線當作零水平集，然后將其擴充到高維水平集函數上，通過求解滿足水平集函數的發展方程，推進水平集演化，此時零水平集也在不斷演化，當演化趨于平穩就得到界面的形狀。水平集方程可以表示為

(7)

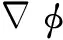
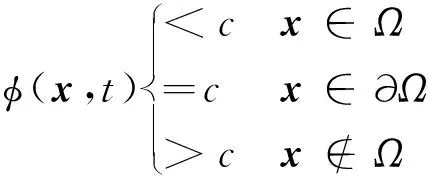
(8)

式中：Ω∈Rn表示一個有界的開區域，?Ω∈Rn表示其邊界。當c=0時，目標集和可達集的邊界可由式(8)中的零水平集函數表示[22]。目標集可表示為

Γ={x∈Rn|φ(x,0)≤0}

(9)

可達集可以通過解如下的Hamilton-Jacobi方程得到：

(10)

式中：

(11)

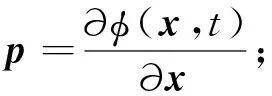
(12)

對于函數φ(x,t)，可達集的隱式表達式為

R(t)={x∈Rn|φ(x,t)≤0}

(13)

從式(11)和式(12)可知，哈密爾頓方程H(x,p)的最大值是通過最優控制u*(x,p)得到，下面介紹如何得到最優控制。

2.3 計算最優控制輸入

最優控制u*(x,p)代表在某一個狀態x下能使哈密爾頓方程H(x,p)達到最大的控制。最優控制輸入u*(x,p)的物理意義可表示為：在控制u*(x,p)的作用下，從初始狀態x出發的軌跡始終能保持在可達集內部并最終到達目標集。通常求解最優控制輸入的過程是一個非凸最優化問題，需要對整個域空間進行搜索，得到能使哈密爾頓方程達到最大的控制。

對于式(1)的方程，迎角α和推力T被作為控制變量。因此最優控制輸入的計算可轉化為求解使H(x,p)達到最大的迎角α和推力T的組合。對于本文的模型，可以簡化為求系統的最優解問題，過程如下：

結合式(2)和式(11)，令

(14)

式中：p1和p2為p的分量。

對于最優控制輸入，在迎角處求偏導，得到

(15)

對式(15)進行分析，能使式(14)取最大值的最優控制如下：

1)當α*=αmin，若p1>0，T*=Tmax；若p1<0，T*=Tmin。

2)當α*=αmax，若p1cosαmax+(p2/V)sinαmax>0，T*=Tmax；若p1cosαmax+(p2/V)sinαmax<0，T*=Tmin。

3)當T*=Tmin，若p1>0，α*=αmax，0或α1；若p1<0，α*=αmax，0。

4)當T*=Tmax，若p1<0，p2>0，α*=αmax；若p1>0，p2<0，α*=0；若p1<0，p2<0，α*=αmax，0；若p1>0，p2>0，α*=0，α2。

其中α1和α2為解式(15)得到的極值點。對以上控制輸入進行分析可知，要使Hamilton-Jacobi方程達到最大的控制輸入可以從以下的6個組合內得到：

(αmin，Tmin),(αmin，Tmax),(αmax，Tmax),(αmax，Tmin),(α1，Tmax),(α2，Tmax)。

3 著陸階段安全分析

本文的案例模型主要參考的是GTM縱向通道模型，在本節中首先基于可達集理論確定飛行安全包線，然后分別研究了襟翼和結冰對安全包線的影響，最后通過對具體的著陸階段進行時域仿真分析，提出了不同結冰條件下的駕駛員應對策略。

3.1 襟翼對安全包線的影響

由于襟翼與著陸過程密切相關，因此本節對襟翼的影響進行具體的分析。襟翼偏角δ通常是從0°到最大值之間變化，本節把襟翼偏角劃分為3個卡位：0°、15°和30°，針對不同卡位計算了相應的升力和阻力。升力和阻力系數曲線分別見圖3和圖4。從圖中可看出，隨著襟翼偏角的增大，升力和阻力都會相應提高。

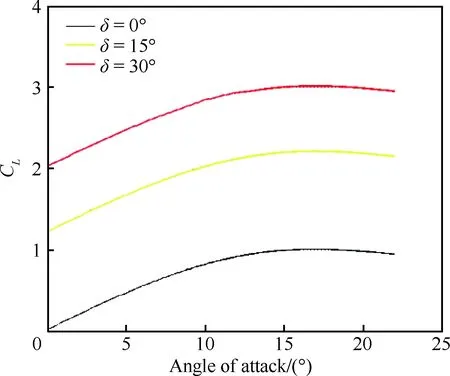
圖3 不同襟翼偏角下的升力系數Fig.3 Lift coefficients for different flap deflections

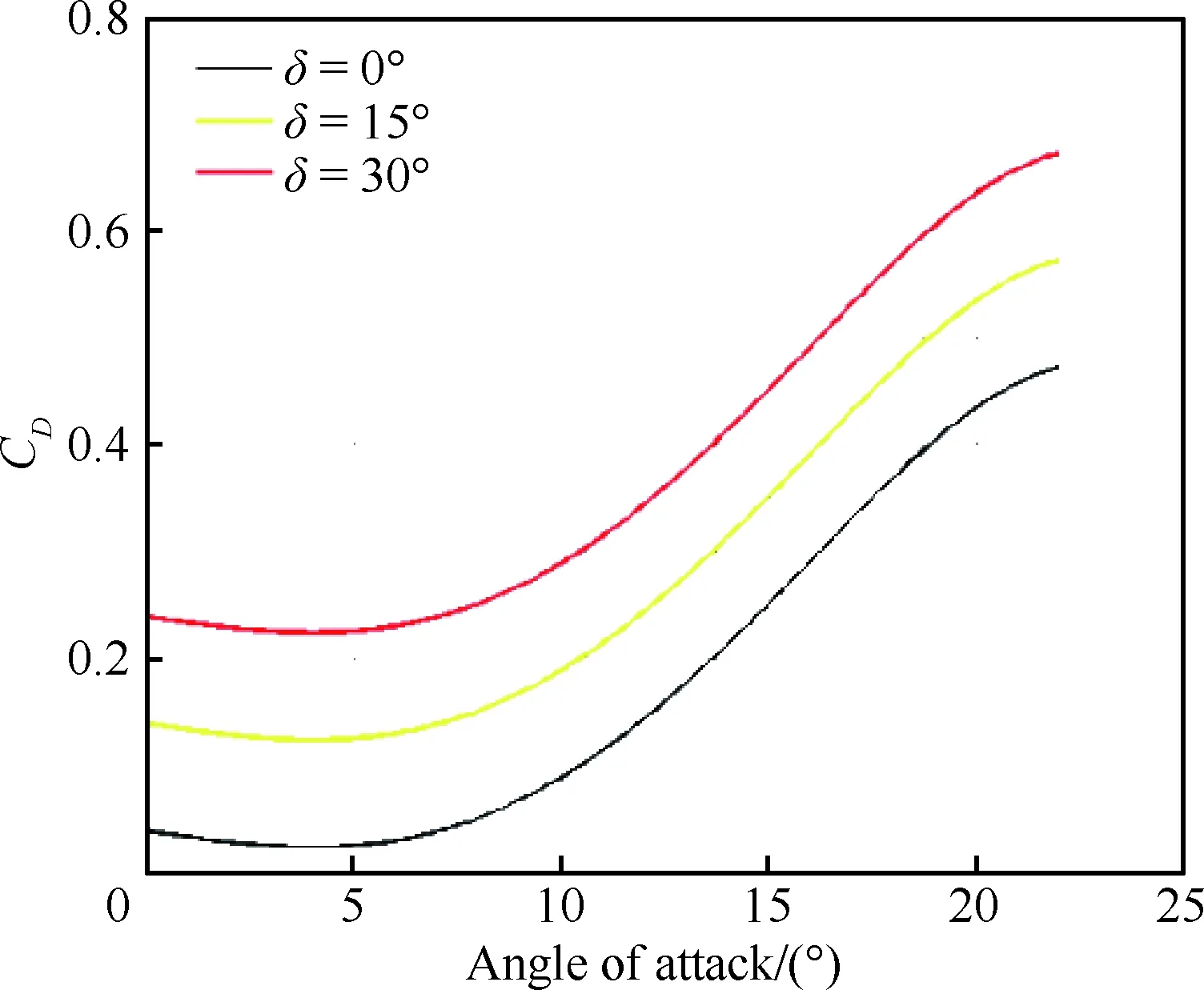
圖4 不同襟翼偏角下的阻力系數Fig.4 Drag coefficients for different flap deflections

對于飛機而言，失速速度可表示為

(16)

式中：CLmax為最大升力系數，為了保證安全，適航標準要求飛機在著陸階段的最小飛行速度不小于1.23VSR(基準失速速度)。這意味著在某個時刻如果飛機的飛行速度低于1.23VSR，其飛行狀態很可能在安全包線以外，本文采用的GTM在不同卡位下的飛行參數限制如表1所示。

表1 GTM在不同襟翼偏角下的飛行參數限制Table 1 Flight parameter limitation ofGTM under different flap deflections

表1中：Vmin、Vmax、γmin和γmax分別為在計算飛機著陸階段可達集時給出的飛行參數約束，并將這些約束作為初始集。其中Vmin的選取標準是使其至少大于1.23VSR，Vmax為根據著陸情況給定的一個最大安全初始速度。從表中可看出最大升力系數隨著襟翼偏角的增大而增大，而飛機的失速速度隨之減小。不同卡位下的可達集如圖5所示。圖5中藍色區域和紅色區域分別表示正向可達集與反向可達集，通過對圖5分析可知可達集隨著襟翼偏角的增大而增大。

圖6為不同卡位(δ=0°，15°，30°)下的飛行安全包線，分別由黑色、紅色、黃色區域表示。對著陸階段而言，增大襟翼偏角能夠提升飛機升力，從而減小失速速度，這樣就能確保飛機著陸時擁有一個更大的可操縱的速度范圍，安全包線也因此增大，因此增大襟翼偏角在一定程度上有助于提升飛行安全。

3.2 結冰對安全包線的影響

按3.1節的分析，襟翼對于提升著陸安全有積極作用。因此，下面對結冰影響的分析是在保證著陸時襟翼偏角為15°的條件下進行的。在區分結冰嚴重程度上課題組在先前已經進行了一定的研究，本文主要參照的是文獻[16]中的結冰程度區分標準，即隨著結冰程度加劇(結冰因子不斷變大)，系統工作點的穩定性質會發生變化，最終將工作點由穩定變為不穩定時的結冰因子定義成重度結冰。因此針對本文所采用的飛機模型，提出了將η=0.1定義為輕度結冰，η=0.2定義為重度結冰。不同結冰條件下的升力系數擬合曲線如圖7所示。其中黑線、黃線、紅線分別表示的是無結冰(η=0)、輕度結冰(η=0.1)、嚴重結冰(η=0.2)時的升力系數曲線。對圖7分析可知，當結冰趨于嚴重時，失速迎角將會快速減小。

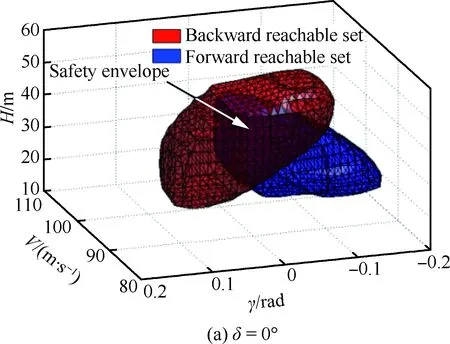
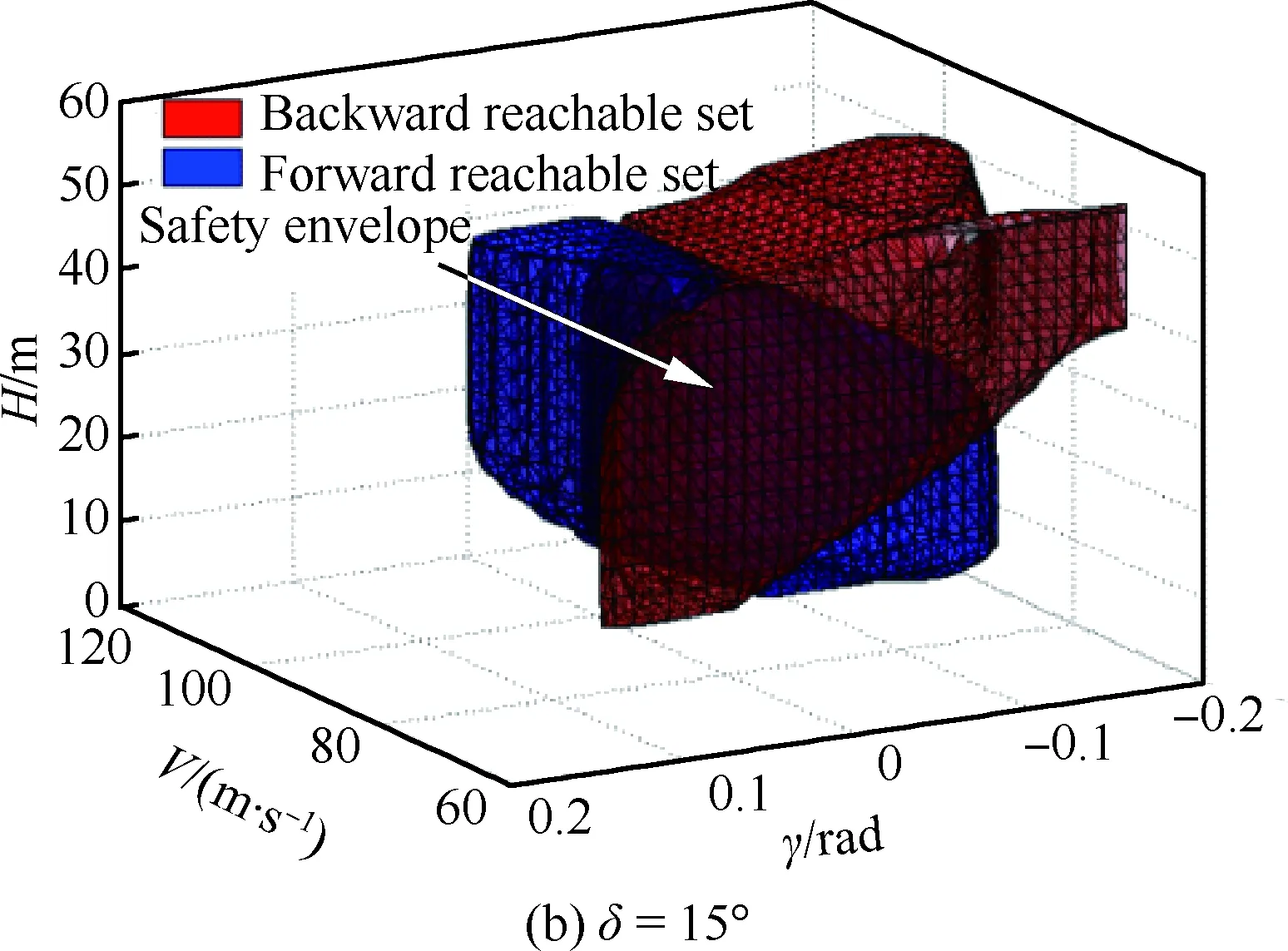
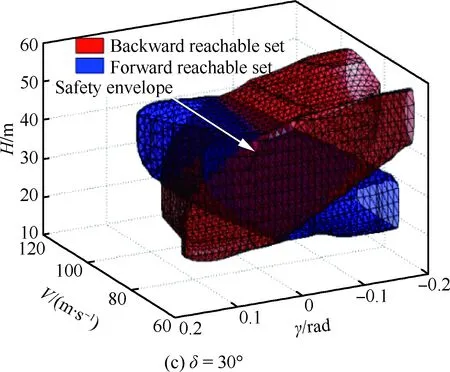
圖5 不同卡位下的可達集(δ=0°，15°，30°)Fig.5 Reachable sets for different modes (δ=0°, 15° and 30°)

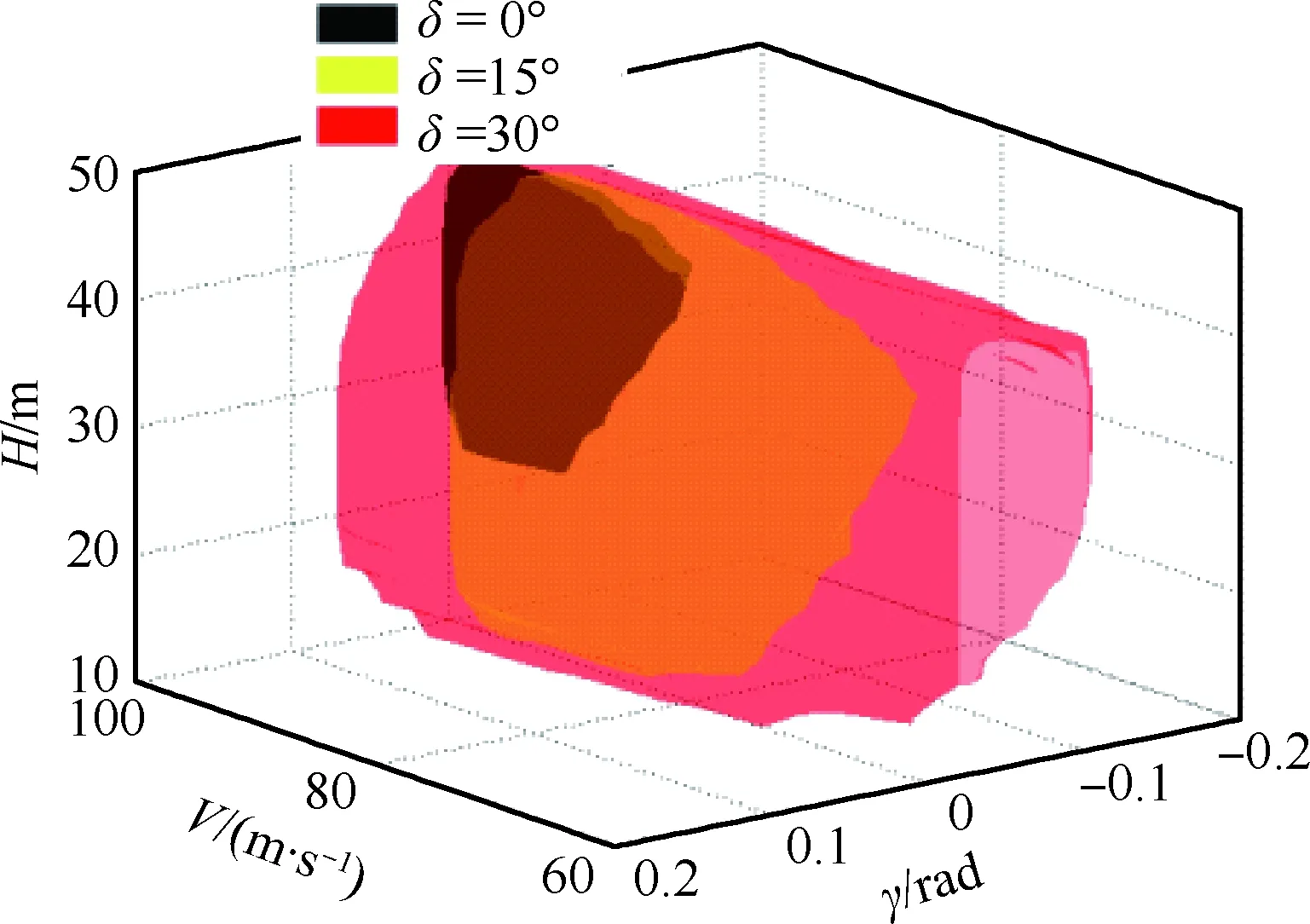
圖6 不同卡位下的飛行安全包線(δ=0°,15°，30°)Fig.6 Flight safety envelopes for different modes (δ=0°, 15° and 30°)

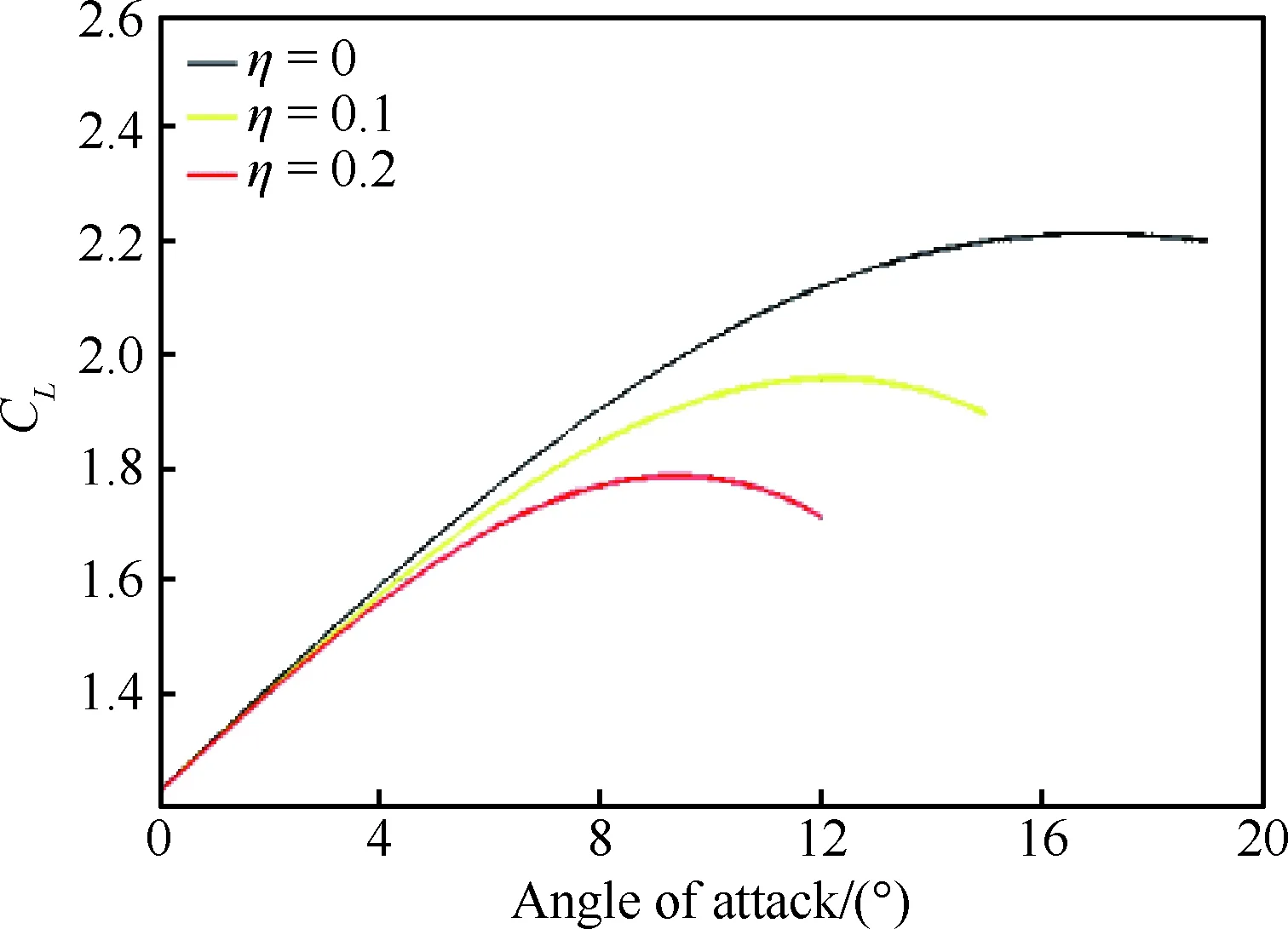
圖7 不同結冰程度下的升力系數Fig.7 Lift coefficients of different degrees of icing

結冰程度增大，最大升力系數隨之減小，失速速度也將發生變化，GTM在不同結冰程度下的飛行參數限制如表2所示。

表2 GTM在不同結冰程度下的飛行參數限制Table 2 Flight parameter limitation of GTMunder different degrees of icing

對于著陸階段，失速速度隨著結冰程度增加而變大，這使得飛機很難達到安全的著陸狀態范圍，因此，此時的飛行包線也將減小。圖8描繪了在不同結冰程度下的飛行安全包線變化(η=0,0.1，0.2)，分別由紅色、黃色、黑色區域表示。對于輕度結冰(η=0.1)，安全著陸速度能到達75 m/s，這能夠保證飛機以正常方式安全著陸。此時，駕駛員仍能夠通過正常操縱使飛行狀態維持在安全包線以內。對于嚴重結冰(η=0.2)，安全包線收縮嚴重，安全著陸速度范圍也隨之減小，能保證安全著陸的最小速度已經超過80 m/s，駕駛員已經很難在最優控制指導下找到安全的著陸軌跡。此時對于駕駛員操縱已經非常困難，著陸風險也隨之增加。因此駕駛員要改變操縱行為，只有當結冰處理后才能繼續著陸。

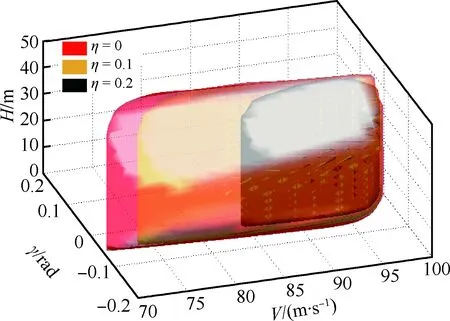
圖8 不同結冰程度下的飛行安全包線Fig.8 Flight safety envelope affected by degree of icing

3.3 駕駛員操縱策略時域仿真

本節主要是針對不同的結冰程度提出相應的操縱策略并對其進行時域仿真驗證。對于輕度結冰，時域仿真從狀態點A(V=91 m/s，γ=-0.034 9 rad,H=40 m)開始到達終點B(V=75 m/s，γ=0 rad,H=0 m)，具體見圖9。紅色和黃色區域分別代表無結冰和輕度結冰時安全包線，黑線代表最優控制下的著陸軌跡，這條軌跡能始終保持在安全包線以內。這表示輕度結冰程度下，飛機仍然能夠通過最優控制方法至少找到一種控制使飛機安全著陸。從而驗證了輕度結冰條件下駕駛員仍然能夠通過正常操縱安全著陸。

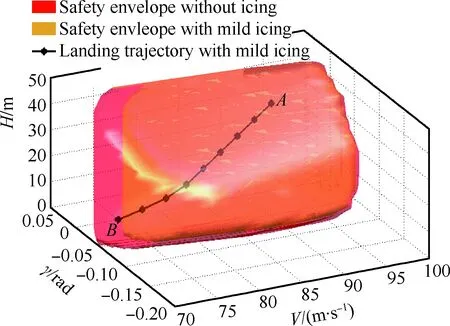
圖9 輕度結冰條件下著陸軌跡Fig.9 Landing trajectory in mild icing condition

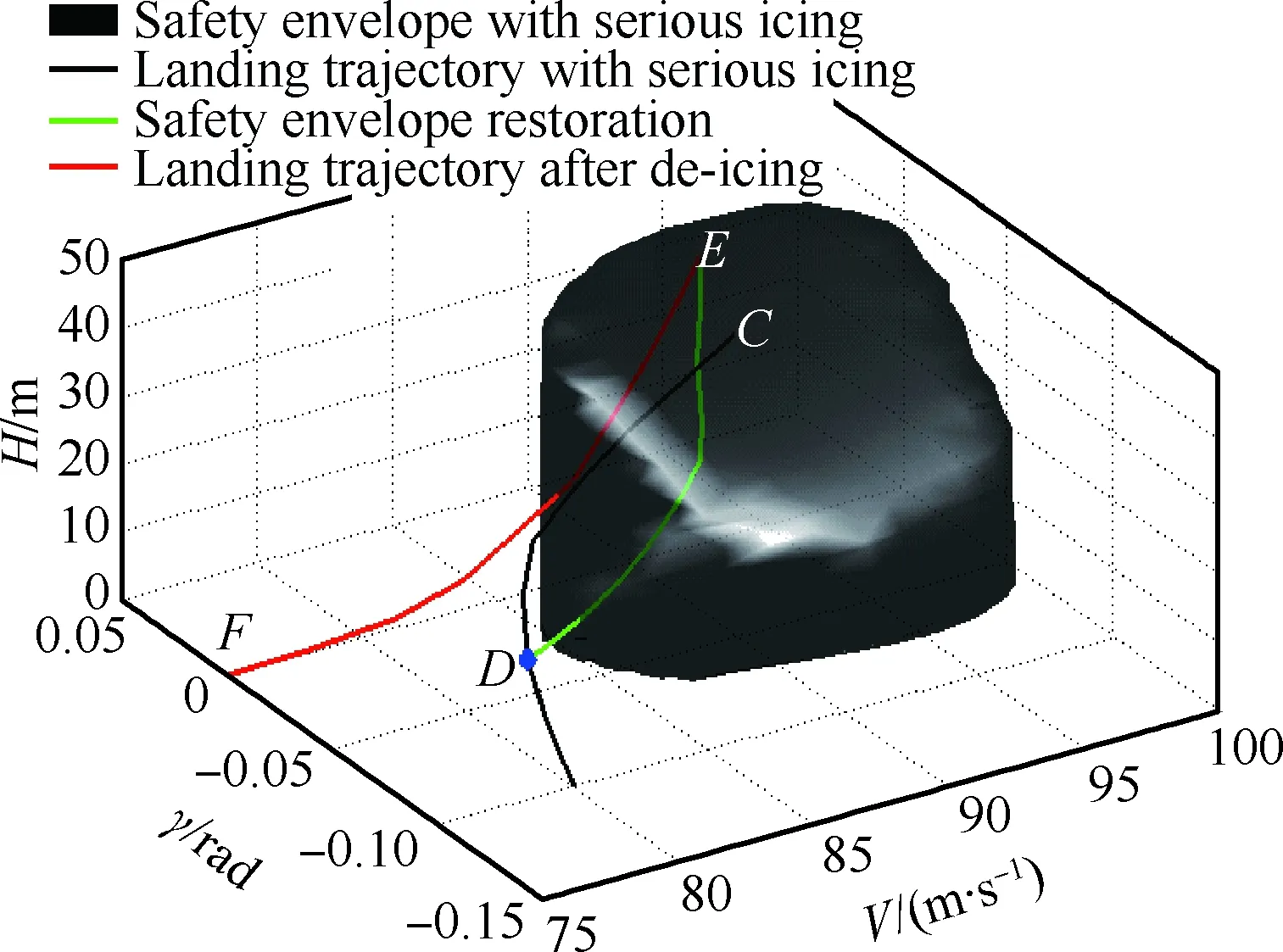
圖10 嚴重結冰條件下著陸軌跡Fig.10 Landing trajectory in serious icing condition

對于嚴重結冰，從初始點C(V=90.77 m/s，γ=-0.044 9 rad,H=41.39 m)處進行時域仿真，具體如圖10所示。黑色曲線代表駕駛員未覺察到結冰時，正常操縱下飛機的著陸軌跡。從圖中可看出，在嚴重結冰時，飛行安全包線已經收縮嚴重，此時已經很難找到一種控制使飛機仍然能夠保持在安全包線以內，如若繼續著陸，飛機將會承受墜毀的風險(如黑色曲線所示)。

由前面分析可知，嚴重結冰時飛機應該停止繼續著陸，并進行邊界恢復操縱，此時可以在狀態點D(V=81 m/s，γ=-0.065 rad,H=10 m)處進行邊界恢復。基于最優控制理論在狀態點D處先以最大推力使飛機重新起飛，然后不斷調整推力T進行邊界恢復，具體控制輸入見圖11。圖10 中的綠線代表邊界恢復曲線，曲線從D開始在圖11的控制作用下重新回到邊界內的狀態點E(V=92.31 m/s，γ=0.007 2 rad,H=44.72 m)。飛機可以在點E附近進行除冰處理，當飛機結冰程度低于輕度結冰(η=0.1)時，飛機可重新進行著陸操縱。圖10中的紅色曲線(曲線從起點E到終點F)為飛機在除冰處理后，重新在最優控制下的著陸曲線。

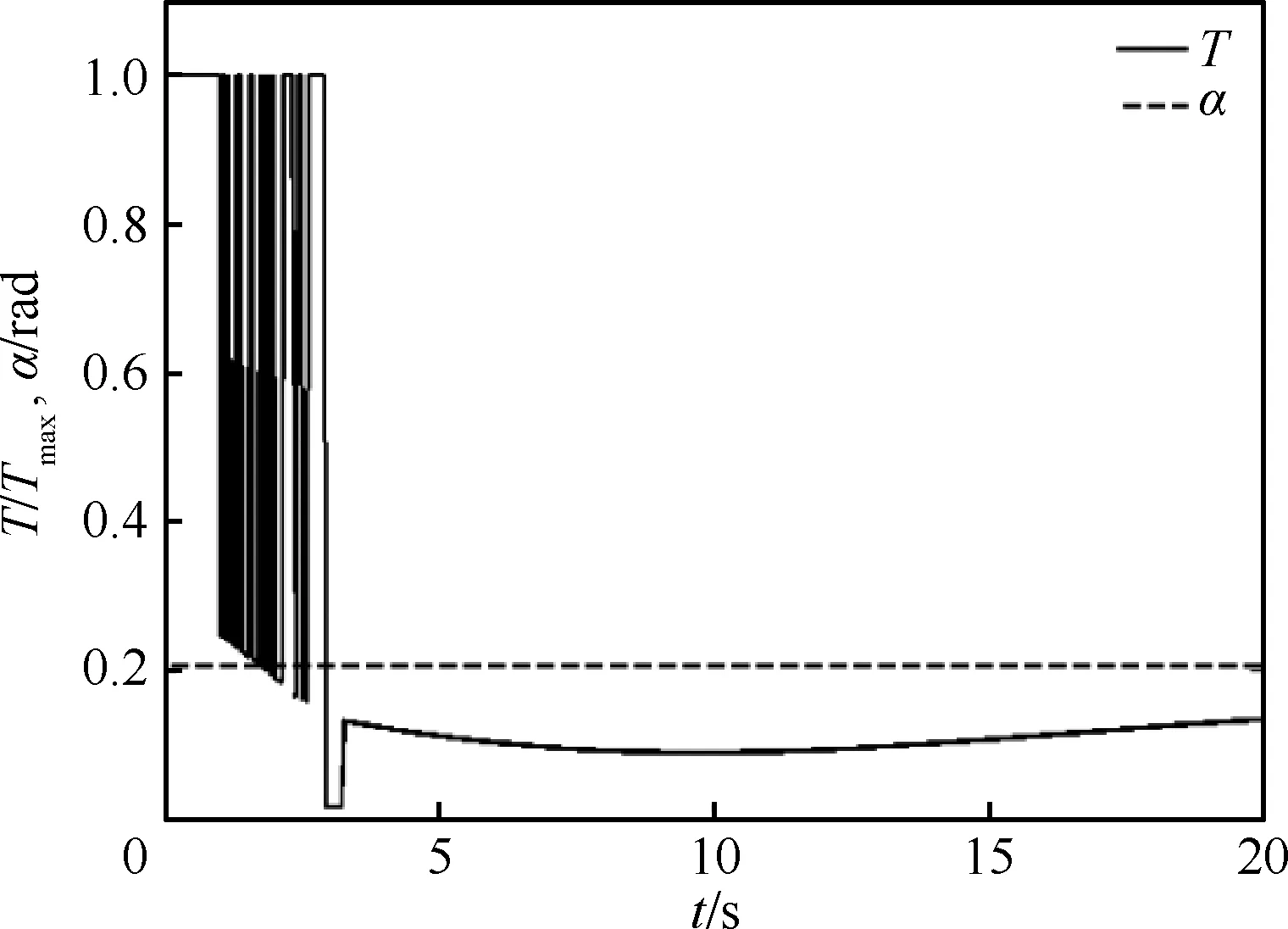
圖11 最優控制輸入時域響應曲線Fig.11 Time domain response curves of optimal control inputs

以上對飛行狀態進行邊界恢復的控制輸入主要是在理想狀態下(不考慮駕駛員的操縱延遲和發動機推力的響應延遲等因素)，通過最優控制使飛機由圖10中飛行安全包線外的狀態點D直接到達包線內的狀態點E。在進入安全包線后的爬升階段，在最優控制指導下對飛機推力的控制也在不斷切換，從而出現了圖11中的劇烈抖動，這種操縱輸入在飛行實踐中可能并不存在。前文中這樣設計只是在理論上對操縱進行了實現，為了滿足工程實踐需求，現給出如下操縱策略(此操縱應對策略來源于前面的理論分析)。首先在狀態點D處以最大推力和最優迎角快速到達包線內的狀態點G，如圖12所示。然后在狀態點G處利用傳統的駕駛員操縱方法使飛機爬升至狀態點H處，其中整個爬升階段的飛行狀態都保持在安全包線以內，爬升軌跡由圖中藍線表示。具體駕駛員操縱見圖13所示。最后在狀態點H附近進行除冰處理，待除冰結束后，重新按照傳統操縱方法進行著陸。圖12中的黃色曲線表示駕駛員按照傳統操縱方法實現的著陸軌跡。通過與最優控制方法所確定的安全著陸軌跡對比可知，在安全包線內，傳統的駕駛員操縱方法也能使飛機安全著陸，這進一步說明了本文提出的安全包線可對結冰條件下的駕駛員操縱進行指導。

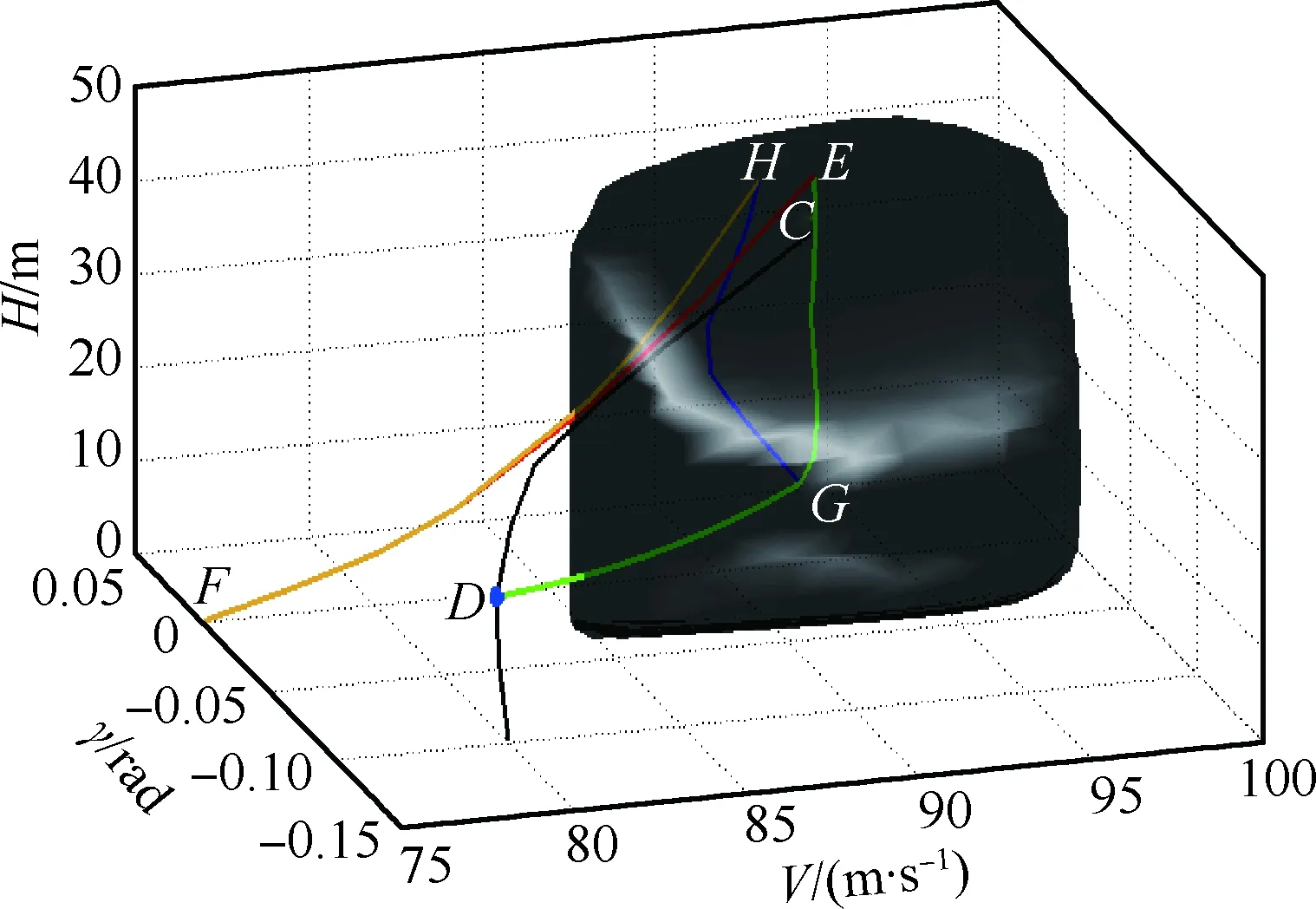
圖12 最優控制與傳統操縱方法著陸軌跡對比Fig.12 Comparison of landing trajectory between optimal control and traditional manipulation method

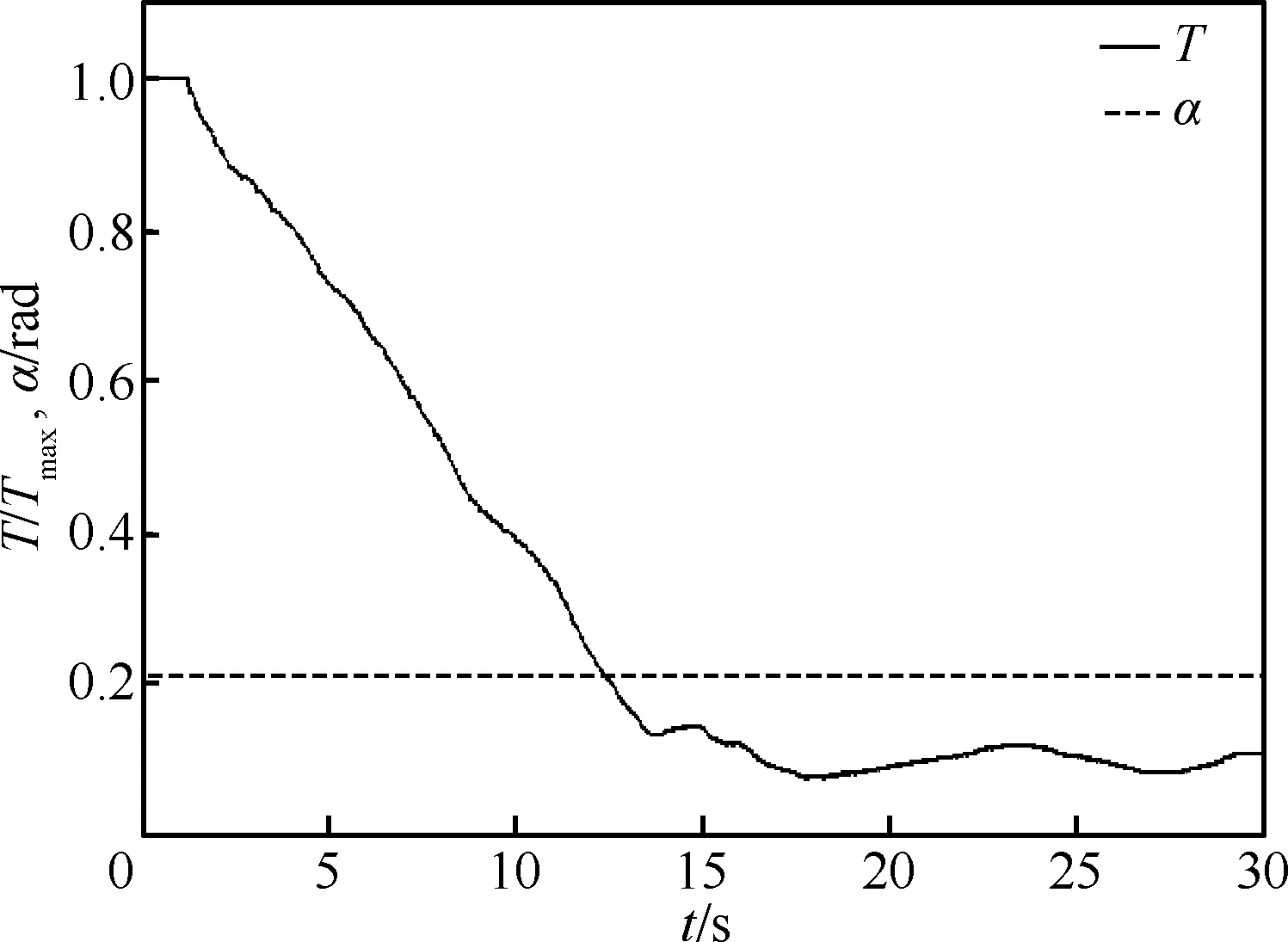
圖13 傳統駕駛員操縱時域響應曲線Fig.13 Time domain response curves of traditional manipulation

4 結 論

本文以GTM為研究對象，提出了基于可達集理論確定結冰飛機在著陸階段的安全包線，通過對結冰后的飛機進行時域操縱驗證，給出了在不同結冰條件下的安全操縱策略，主要成果如下：

1) 駕駛員在未察覺到結冰時操縱極易使飛行狀態超出安全包線，基于可達集理論確定的安全包線能夠突破傳統包線的限制，適用于不同程度的結冰條件安全性分析。

2) 將正向可達集與反向可達集的交集作為飛行安全包線，可以確保飛行狀態能始終在最優控制下保持在安全包線之內，這對于確保著陸安全具有重要意義。

3) 不同程度的結冰條件應給出不同的應對策略。對于輕度結冰，在飛行包線內仍然能通過最優控制使飛機安全著陸。而對于嚴重結冰，飛行包線收縮嚴重，常規操縱已經很難保證飛機繼續安全著陸，此時必須在著陸軌跡的某個狀態點處進行邊界恢復操縱，使飛行狀態重新回到安全包線內，待除冰完成后再繼續進行著陸。