臨近空間高超聲速跳躍滑翔式目標自適應跟蹤模型

李凡，熊家軍

1. 空軍預警學院 研究生大隊，武漢 430019 2. 空軍預警學院 預警情報系，武漢 430019

臨近空間高超聲速飛行器(Near Space Hypersonic Vehicles, NSHV)是指飛行于20～100 km 高度空域，飛行馬赫數大于5，具有執行快速打擊任務能力的飛行器。相對常規飛機目標而言，NSHV速度快、飛行高度高；相對彈道導彈目標NSHV機動能力強、飛行軌跡靈活、突防能力強[1-2]。當前，無論是作為進攻或防御方對于NSHV的研究都如火如荼地展開，其中，臨近空間高超聲速跳躍滑翔式目標飛行軌跡更加復雜多變，機動突防能力強，對此類目標的高精度跟蹤是實現高精度預警攔截的關鍵技術之一[3-4]。

眾所周知，機動目標跟蹤模型分為運動學與動力學模型兩大類[5-7]，而臨近空間高超聲速跳躍滑翔式目標跟蹤也屬于機動目標跟蹤范疇，對這類目標的跟蹤模型同樣可以以此進行區分。動力學模型以目標受力為起點，包括重力、空氣動力、阻力及推力，分析不同類型的力產生加速度，以實現對目標真實運動的描述[8-10]。動力學模型適用于受力相對簡單的目標跟蹤，其最早應用于彈道目標的跟蹤及落點預報，臨近空間高超聲速跳躍滑翔式目標速度較快無法實現瞬態的強機動。同時，在實際的制導與控制設計中，控制量相對較為簡單，迎角與傾側角模型通常采用簡單函數描述。此外，臨近空間高超聲速跳躍滑翔式目標可以在臨近空間中長時間滑翔飛行，受力影響較少且較為穩定(相對飛機等在線控制目標)，因此動力學模型也可適用于這類目標跟蹤[11]。動力學模型優點在于模型包含的信息量較大，能得到多種氣動及運動參量等，對目標運動描述的精度較高，但需要的先驗信息較多，當先驗假設與實際不匹配時，模型退化嚴重誤差較大。當前對于臨近空間高超聲速跳躍滑翔式目標跟蹤動力學模型研究聚焦于加速度表達、制導及控制參數的辨識及引入[12]。

運動學模型直接以加速度為起點，通過經典運動模型得到目標的狀態估計[13-14]。運動學模型是最為傳統的跟蹤模型，基本可以運用于所有機動目標的跟蹤(包括彈道目標、飛機等在線控制目標)，其優點在于適應性較好，模型結構較為簡單，先驗信息需求少，但其性能依賴于對加速度的機動統計建模，當前已有的白噪聲勻速(Constant Velocity, CV)/勻加速(Constant Acceleration, CA)模型、一階指數相關Singer模型、Jerk模型、非零均值一階指數相關“當前”統計(Current Statistical, CS)模型等，對臨近空間高超聲速跳躍滑翔式目標跟蹤效果并不十分理想[15-16]。在此基礎上，文獻[17]首先提出了具有周期特性的二階正弦波(Sine Wave, SW)相關模型，SW模型認為這類目標加速度相關性服從正/余弦的周期性質，周期性引入能更加準確地描述跳躍式軌跡的運動特性，這一模型對臨近空間高超聲速跳躍滑翔式目標跟蹤運動學建模影響較大。

文獻[18]指出自適應非零均值模型性能一般情況下略優于零均值模型，且適應性較強，當前對于一階指數相關Singer模型，其自適應非零均值形式CS模型研究較為成熟，而SW的非零均值形式還未出現公開資料，本文在SW基礎上提出了自適應非零均值SW(Adaptive Non-zero Mean Sine Wave, ANM-SW)模型。首先從非零均值機理出發構建了ANM-SW模型，推導了模型狀態方程，在此基礎上闡述了自適應非零均值模型的物理含義；此后結合卡爾曼濾波(Kalman Filter, KF)從系統動態誤差穩態分析了ANM-SW及SW模型的性能差異；最后進行了一系列的仿真驗證。

1 自適應非零均值模型

非零均值模型實質是通過引入加速度均值，使得加速度分布隨均值移動，鑒于非零均值時間相關模型優越性能，本文在此直接討論非零均值模型的情況，并構建ANM-SW模型。假定目標加速度為加速度均值與相關擾動組合而成[18],即

(1)

1.1 ANM-SW連續時間模型

王國宏等[17]針對跳躍滑翔式軌跡縱向近似正/余弦函數的特點(由于正弦、余弦周期性推導的結果相同，本文統稱為SW)，認為其加速度等表現出類似的周期性質，根據這一特性，SW模型假設加速度自相關函數為

(2)

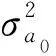
(3)

式中：ω(t)為白噪聲輸入，且存在

(4)

在SW模型的微分方程基礎上引入加速度非零均值，結合式(1)和式(3)可得ANM-SW模型的微分方程為

(5)

式(5)構造了完整的ANM-SW二階Markov時間相關模型，因此ANM-SW模型連續時間狀態方程為

(6)

式(6)為ANM-SW加速度均值補償的微分方程，可簡化為

(7)

式中：X(t)為狀態向量；AANM-SW為連續時間狀態轉移矩陣；U1、U2和U3為控制矩陣；B=[0,0,0,1]T為噪聲向量。

1.2 均值補償

根據式(7)可得狀態轉移矩陣F(T,β)為

F(T,β)=eAANM-SWT=

(8)

式中：T為跟蹤采樣時間間隔。

(9)

(10)

(11)

(12)

式中:Ⅰ部分

令x=(k+1)T-ξ?

(13)

Ⅲ部分

令x=(k+1)t-ξ?

(14)

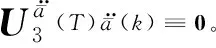
則ANM-SW模型離散狀態方程為

X(k+1)=F(β,T)X(k)+

(15)

式中：X(k+1)為離散時間狀態向量；W(k)為過程噪聲。根據式(15)可知ANM-SW模型狀態的預測為

(16)

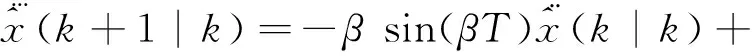
(17)

(18)

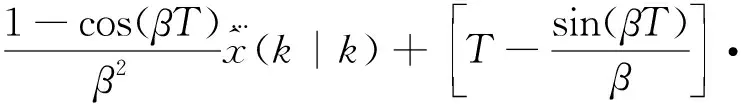
(19)

(20)

將式(17)和式(20)合成，則均值補償后的ANM-SW模型狀態預測表達式為

(21)

式中：Φ(T)為狀態轉移矩陣，式(2)體現了自適應非零均值加速度引入的物理本質，ANM-SW模型的狀態預測變為了基本的勻加加速度模型，類比于CA模型，在此將勻加加速度模型簡稱為CJ(Constant Jerk)模型。

如前所述，ANM-SW模型經過均值補償后與CJ模型的運動方程一致，即狀態轉移矩陣僅與時間間隔T相關，與其他參數無關。無論是一階還是二階的Markov時間相關模型，加速度相關假設條件下的狀態轉移矩陣，不再符合對經典力學領域中物體運動形式的認知，即位移為速度、加速度等狀態量的時間積分之和。而自適應非零均值Markov模型彌補了這一缺陷，其物理實質在時域方面體現為通過加速度/加加速度均值補償，使得狀態轉移矩陣依舊服從對運動的認知，即狀態轉移矩陣Φ(T)僅受采樣間隔T影響；在頻域方面表現為矩陣A中先驗假設參量β的對消，使其呈現為標準的0-1矩陣(參見2.3節)，保證頻域上的濾波器呈線性系統，增強了模型對不同機動樣式的適應性。

1.3 過程噪聲協方差自適應

(22)

2 ANM-SW模型的KF性能分析

機動目標跟蹤算法包括機動模型和濾波算法2個方面，整體性能同時依賴模型和濾波算法的相互作用，為進一步分析ANM-SW模型性能改善，首先基于KF推導了跟蹤算法狀態更新的系統動態誤差[18]，并設定了3種典型的運動形式，然后分別結合SW、ANM-SW模型對比分析了其動態誤差穩態值，說明了ANM-SW模型較SW模型的優勢。

2.1 KF狀態更新動態誤差分析

狀態更新主要受模型狀態方程及濾波增益影響，設系統連續時間量測方程為[19]

Z(t)=H(t)X(t)+V(t)

(23)

式中：Z(t)和H(t)分別為量測向量和量測矩陣；V(t)為量測噪聲，E(V(t)VT(t))=R(t)。根據卡爾曼濾波理論，連續時間狀態估計為

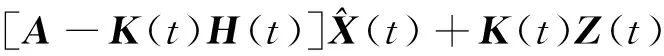
(24)

式中：K(t)為增益矩陣，當濾波達到相對穩態時，增益能較為準確地描述量測噪聲的分布特性，此時增益趨于常值，本文在此僅考慮一維的情況，即H(t)=H=[1,0,0,0]T，則式(24)的拉普拉斯變換為(假設初始條件為零)

(25)

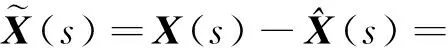
(26)

若目標的機動表現為加速度的單位脈沖函數、單位階躍函數、單位斜坡函數3種不同情況時，可得到SW、ANM-SW模型狀態更新中動態誤差的穩態值。

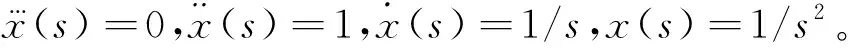
2.2 SW模型動態誤差穩態

(27)

式中:

則SW模型動態誤差穩態為

(28)

對于SW模型，當目標機動形式為Case 1時，SW模型動態誤差穩態為零。當為Case 2、Case 3時，SW模型難以保證狀態更新的誤差穩態趨近于0，表明當出現Case 2、Case 3時使用SW模型，狀態估計的收斂性存在一定風險。針對這一問題，一方面，可以通過合理的參數取值限制模型動態誤差穩態的大小；另一方面，使用采用自適應非零均值模型強制模型收斂。

2.3 ANM-SW模型動態誤差穩態

ANM-SW模型狀態轉移矩陣都滿足勻加加速度形式，則ANM-SW模型等價的連續時間狀態微分方程為

(29)

(30)

當加速度輸入為Case 1、Case 2、Case 3時，ANM-SW模型狀態更新的動態誤差穩態恒為0，自適應非零均值模型通過均值補償實現了對模型參數的簡化，消去了先驗相關性假設參數，進而重新形成勻加加速度的形式，在狀態更新的動態誤差穩態上體現為分子上的零點數量增加，保證了對3種不同加速度輸入條件下系統動態誤差穩態的收斂性能[19-20]。

3 仿真分析

本文設置2個不同的仿真場景，其中場景Ⅰ用于驗證ANM-SW模型用于跟蹤臨近空間高超聲速跳躍滑翔式目標軌跡的跟蹤精度優越性。仿真場景Ⅱ用于分析ANM-SW模型對典型運動適應性。

3.1 場景Ⅰ

圖1 周期軌跡Fig.1 Periodic trajectory

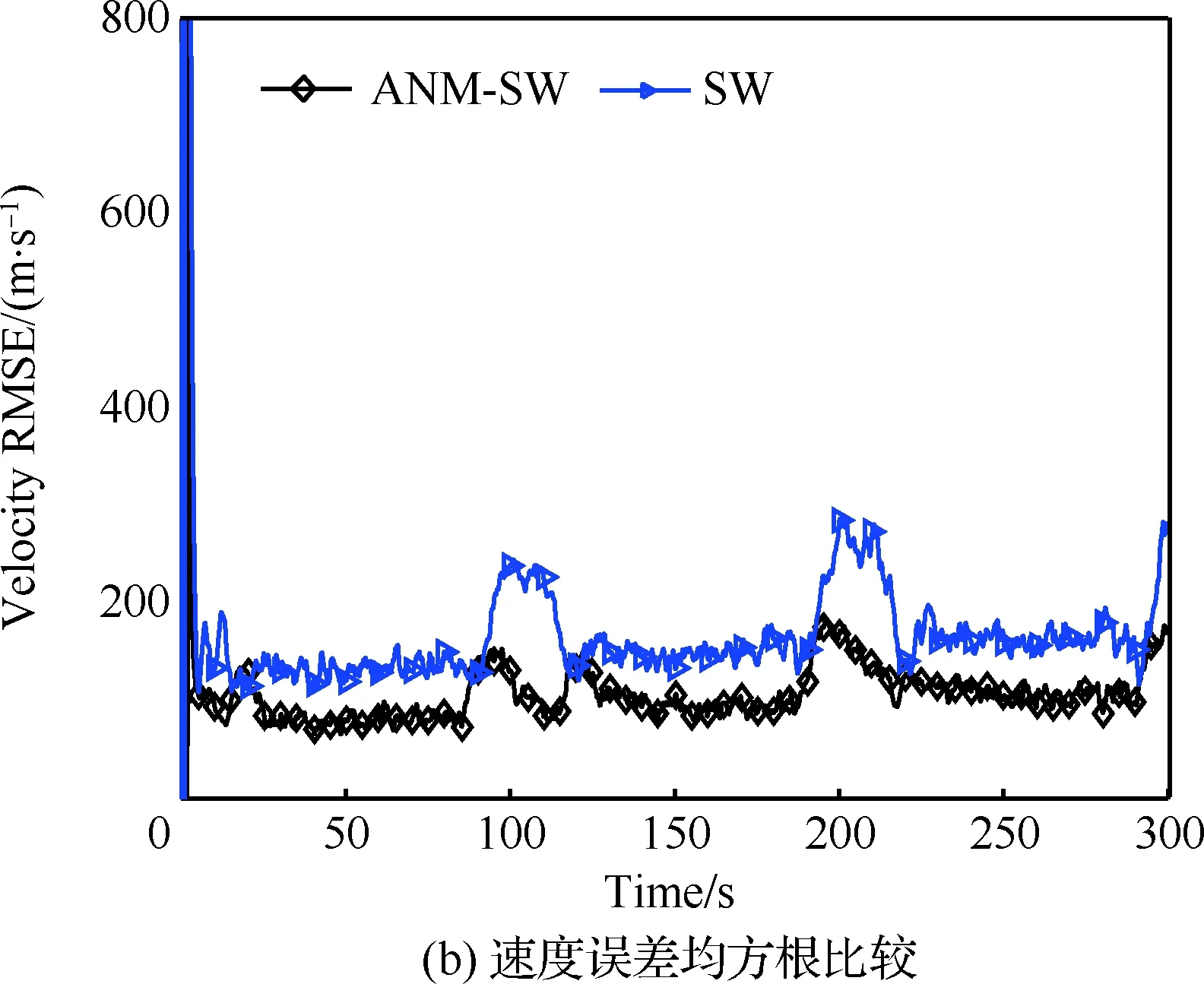
圖2 周期軌跡濾波仿真結果Fig.2 Simulation results of periodic trajectory filtering

文獻[15, 17]中已經驗證，具有類周期特性的SW模型能更加準確描述跳躍滑翔式目標運動特性，相對常規的Singer、CS等模型跟蹤精度較高。在位置誤差方面，如圖2(a)所示，2種模型位置誤差呈緩慢上升趨勢，總體水平較為穩定。其中SW模型誤差較高，且波動幅度略大，在100 s和200 s附近由于強機動有明顯的誤差上升。ANM-SW模型整體誤差水平平穩，100 s和200 s時刻誤差沒有出現突變，在強機動位置時能較好地壓制誤差上升，其跟蹤精度略優于SW模型。

在速度誤差方面，如圖2(b)所示，SW模型誤差較高，在強機動時速度誤差迅速上升，在一段時間內保持較高誤差水平狀態，難以快速收斂至較低水平。ANM-SW模型誤差整體水平較低，自適應非零均值模型能快速描述目標的速度變化，特別是在強機動時，能有效壓制誤差升高，收斂速度較快。為更好比較各模型的跟蹤性能，計算所有模型的位置及速度誤差統計平均如表1所示(本文約定從誤差收斂時開始統計平均)。

表1 位置與速度誤差統計平均Table 1 Statistical average of position and velocity errors

3.2 場景Ⅱ

3.2.1 自適應非零均值模型適應性

此前從時域的狀態方程、頻域的系統動態誤差穩態分析了ANM-SW模型的物理本質，證明了自適應非零均值模型對機動的適應性更好。因此，分別設定勻加速、脈沖加速、正弦加速3種運動(一維軌跡)，討論了模型對不同運動的跟蹤效果，并分析了目標狀態估計的一致性。其中3種運動的加速度如圖3所示。

跟蹤CA運動效果如圖4所示，SW模型假定目標加速度相關完全服從周期性，導致濾波誤差較大，位置、速度及加速度誤差均高于ANM-SW模型。此外，由于目標做勻加速運動，跟蹤誤差經過最初階段調整后整體較為穩定。ANM-SW模型通過均值補償，使得狀態方程呈現勻加加速度形式，對CA運動濾波精度遠高于SW模型。

設置脈沖加速運動主要為了檢驗模型對加速度突變的適應能力，如圖5所示，SW模型在40 s及60 s加速度突變時表現欠佳。其中SW模型位置誤差在40 s時急劇升高，且在40 s～70 s內的誤差維持較高水平，難以恢復至40 s前誤差水平，此外，SW模型對速度、加速度誤差有一定的抑制能力，其誤差曲線突變后有一定回落，但其適應能力有限，速度及加速度整體誤差依然較高。ANM-SW模型能快速描述目標機動變化，在40 s及60 s時刻位置誤差沒有出現大幅度突變，僅有小范圍的誤差升高，40～60 s內目標做勻加速運動，由于ANM-SW模型狀態方程呈現CJ形式，能較好適應這一時段內的運動模式，其位置誤差可類比CA運動的跟蹤濾波，速度及加速度誤差方面，如圖5(b)和圖5(c)所示，在40 s和60 s機動突變時，其速度及加速度誤差急劇上升后迅速收斂至較低水平，與CA運動的濾波誤差相近。

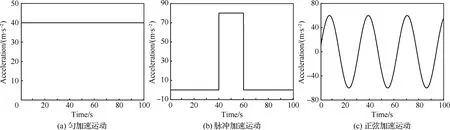
圖3 3種運動的加速度曲線Fig.3 Curves of three motions of acceleration

圖4 勻加速運動跟蹤結果比較Fig.4 Comparison of tracking results of constant acceleration motion

圖5 脈沖加速運動跟蹤結果比較Fig.5 Comparison of tracking results of pulse acceleration motion

正弦加速運動跟蹤結果如圖6所示，由于目標加速度呈周期性變化，導致SW及ANM-SW模型的位置、速度、加速度誤差呈周期性波動，SW模型誤差波動幅度較大。由于SW模型加速度自相關完全服從周期性的假設，對正弦加速運動具有較高的跟蹤精度，其誤差均值略小于ANM-SW模型，但其缺點在于對目標機動難以快速反應，如圖6(c)中SW模型加速度誤差與加速度大小存在一定的時延。而ANM-SW模型通過均值補償能快速適應目標機動變化，其誤差相對波動較小，但均值補償使得ANM-SW模型中周期性被削弱，其誤差整體水平略高于SW模型。總體而言，跟蹤正弦運動時SW模型效果略優于ANM-SW模型。此外，SW誤差谷值點遠小于ANM-SW模型的，但其峰值點與SW模型相當甚至略高，因此跟蹤正弦加速運動目標時，ANM-SW模型穩定性較好，不失為一種較為穩妥的方案，而SW模型濾波誤差谷值點具有更高的精度潛力，可用于交互多模型(Interacting Multiplc Model, IMM)構建新的多模型結構跟蹤這一運動形式目標，以追求更準確的狀態估計。為更直觀比較模型性能，場景Ⅱ中濾波誤差統計平均如表2所示。

3.2.2 狀態誤差一致性

對于隨機參數而言，其估計均方收斂的條件為

(31)

(32)

若狀態估計無偏，且式(32)成立，則認為該濾波器的狀態估計是一致的(其本質為有限樣本一致性)。令歸一化狀態估計誤差平方為

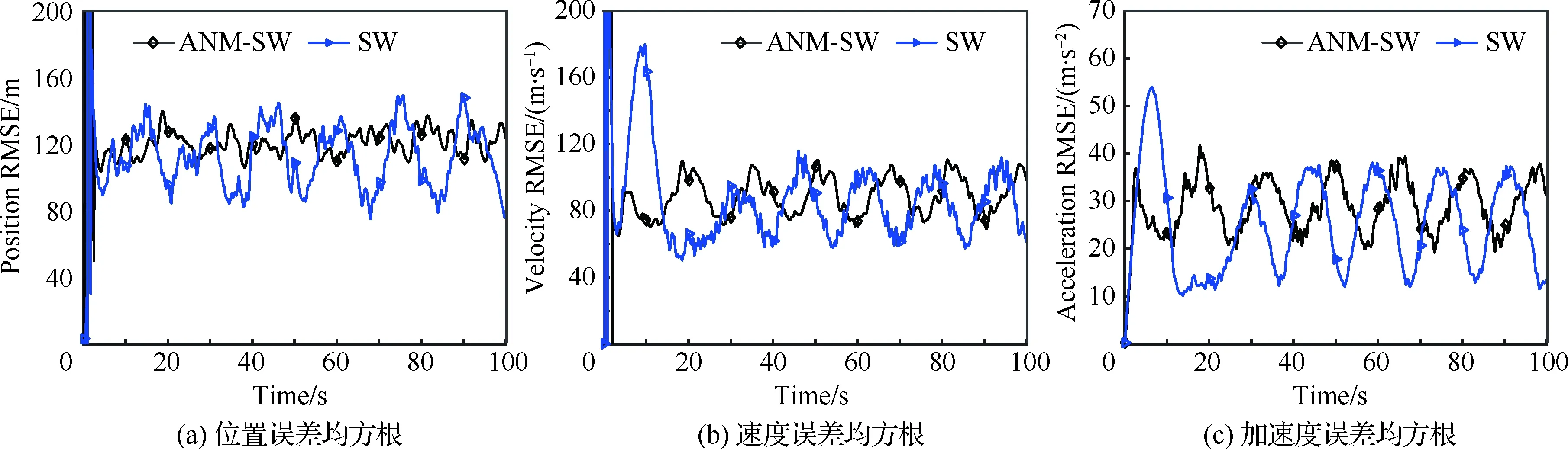
圖6 正弦加速運動跟蹤結果比較Fig.6 Comparison of tracking results of acceleration motion

表2 跟蹤不同運動時位置、速度及加速度誤差統計平均Table 2 Statistical average of position, velocity and acceleration errors in tracking different movements

ModelConstant acceleration motionPulse acceleration motionSinusoidal acceleration motionPosition error/mVelocity error/(m·s-1)Acceleration error/(m·s-2)Position error/mVelocity error/(m·s-1)Acceleration error/(m·s-2)Position error/mVelocity error/(m·s-1)Acceleration error/(m·s-2)SW1931244219289261188225ANM-SW113541613361161298825

(33)

(34)

圖7 狀態估計一致性比較Fig.7 Comparison of state estimation consistency

式時，SW及ANM-SW模型都不具備狀態誤差與濾波計算協方差一致性，跟蹤勻加速運動及脈沖加速運動時，ANM-SW模型狀態誤差一致性較為穩定，且略好于SW模型。跟蹤正弦加速運動時，SW模型狀態誤差一致性波動較大，其波谷與置信區間接近，但波峰較高，偏離置信區間大，ANM-SW模型狀態誤差一致性起伏相對較小，其均值與SW模型相近。結合表2中數值統計結果可知，跟蹤勻加速及脈沖加速運動時，本文模型跟蹤性能明顯占優。跟蹤正弦加速運動時，SW模型略優于本文模型，兩種模型濾波性能差距較小。因此，就總體的模型適應性而言，本文模型是較為安全穩妥的選擇。

4 結 論

針對臨近空間高超聲速跳躍滑翔式目標跟蹤問題，基于SW模型對臨近空間高超聲速跳躍滑翔式目標類周期運動精確描述的基礎上，考慮到自適應非零均值的機動適應能力，提出了一種自適應非零均值正弦波ANM-SW模型。并分析了ANM-SW模型與一階Markov自適應非零均值模型的差別，此后，結合Kalman濾波推導ANM-SW模型動態誤差，驗證了ANM-SW模型機動適應性。仿真結果跟蹤臨近空間高超聲速跳躍滑翔式目標時，ANM-SW模型跟蹤精度高于SW模型，并通過設置不同運動模式分析驗證了ANM-SW模型在機動適應方面的優越性。