復雜電磁環境中無源干擾對艦載雷達效能的影響研究

程占昕，閆仲鈺

(1.海軍大連艦艇學院，遼寧 大連 116018；2.北部戰區海軍聯合海情預警中心，山東 青島 266001)

0 引 言

現代海戰是在復雜電磁環境下的信息體系的對抗，雷達作為水面艦艇信息獲取的主要手段，如何在復雜電磁環境下充分發揮其應有的作戰效能，是一個迫切需要研究和探討的課題。復雜電磁環境的顯著特點是電磁信號特性復雜、電磁信號密度高、電磁信號干擾強度大、電磁信號危害大。復雜電磁環境的干擾包含有源和無源干擾信號，而無源干擾信號是始終存在的。因此，深入探討復雜電磁環境中無源干擾對艦載雷達使用效能的影響，對于充分發揮艦載雷達的作戰效能具有重要的意義[1]。

本文主要研究敵方釋放的無源干擾，特別是敵方干擾飛機。在飛機對水面艦艇攻擊的過程中，無源干擾通常在伴隨掩護攻擊機群的情況下施放，距離艦船60 km左右，高度3 km左右，布放長度為10～60 km的無源干擾云帶。在干擾彈投放后的最初10 min內，無源干擾反射器的分散情況，相對投放點在水平面和垂直面上均應服從高斯分布定律[2-3]。

1 無源干擾特性分析

1.1 無源干擾的密度

理想狀態下，若在布放的立體空間中有70%的具有一定密度的反射器，則單架飛機在垂直于進攻方向上可形成一個橢圓形干擾區，該飛機施放的偶極子反射云的體密度[1]為：

(1)

式中：Q為偶極子反射器滿載重量；q為每束偶極子反射器重量；Ldo為飛機的飛行距離；Nn為每束中偶極子的數量；α為利用系數；αx、αy為垂直于飛行方向的平面內偶極子散射的均方差值。

為方便起見，我們可利用無源干擾的線性密度，即：

(束/100m)

(2)

偶極子反射器的下降速度決定了偶極子反射器在空中的駐留時間，通常情況下為6～10 m/s，因此在正常大氣壓下，其駐留時間一般為數十分鐘到數小時不等。

1.2 標準相關函數

在實際中，由于復雜因素的影響，所反射的艦載雷達信號會產生起伏，這些因素包括：

(1) 每個偶極子反射器的隨機漂移；

(2) 雷達天線轉動或艦艇航行；

(3) 艦載雷達工作頻率變化。

偶極子反射體反射的信號瞬時值的概率密度分布規律應滿足高斯定律。因此來自偶極子反射體反射的信號，其標準相關函數可用下式計算：

(3)

式中：k0i(τ)為引起信號起伏的第i個因素的信號標準相關函數；m為引起信號起伏因素總的個數。

由偶極子反射器隨機漂移的所引起的相關函數為：

(4)

式中：v0為反射器運動速度的均方差值；λ為艦載雷達信號波長。

理論上精確計算k01(τ)是比較困難的，這里給出其標準相關譜值，如表1所示。

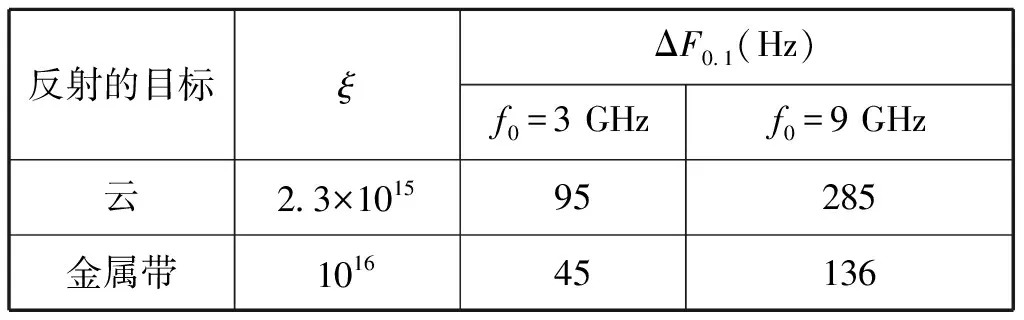
表1 標準相關譜

隨著艦載雷達天線的轉動，雷達波束在空間范圍內掃描會發生變化，同樣拓寬起伏信號的相關譜會引起反射信號的非相關。因此，體分布目標信號的標準相關函數可用下式計算：

(5)

式中：ωβ為艦載雷達天線旋轉角速度；Δβ為艦載雷達天線水平波束寬度。

同時，艦載雷達航行時也會引起反射信號相位的變化和反射信號的起伏，因此體分布目標信號的標準相關函數可用下式計算：

(6)

其中：

(7)

式中：vα為艦艇的航速；β0為艦艇航向與天線波束指向之間的夾角。

艦載雷達的工作頻率的改變也會引起起伏，這是因為信號相位是變化的。頻率變化Δf的信號之間的相關函數K04如圖1所示。

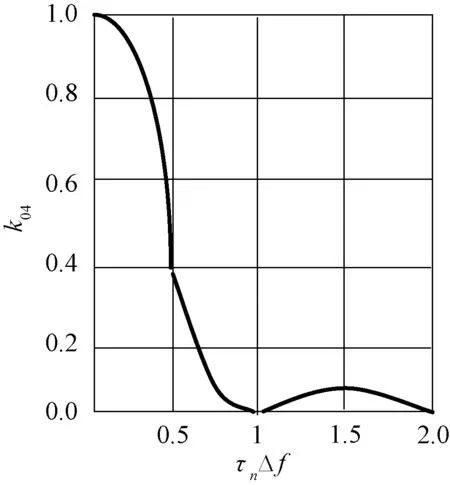
圖1 振蕩頻率變化引起的相關函數

由圖1可以看出，K04=0.2時的相關帶為0.7τnΔf。綜合考慮上述因素，可以得出無源干擾相關函數為：

K0(τ)=K01(τ)K02(τ)K03(τ)K04

(8)

2 無源干擾對艦載雷達效能的影響

2.1 艦載雷達發現效能概率

表征艦載雷達效能的指標有很多，這里采用發現效能概率來表示[2-3]，即：

(9)

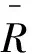
Φ(x)函數為：

(10)

2.2 無源干擾的功率

艦載雷達接收分系統能夠接收到的無源干擾平均功率可用下式計算：

(11)

式中：ph為雷達發射機脈沖功率；λ為雷達工作波長；R為目標距離；G(β,ε)為艦載雷達天線增益；η為艦載雷達指定空域內體分布目標的有效散射面積；knn為干擾功率在空間、波導等所有傳播路徑上的衰減因子；v為場衰減乘積系數。

其中，無源干擾帶的有效雷達橫截面積(RCS)可用下式計算：

η=η0vp

(12)

式中：vp為艦載雷達照射空域的體積，如圖2所示。

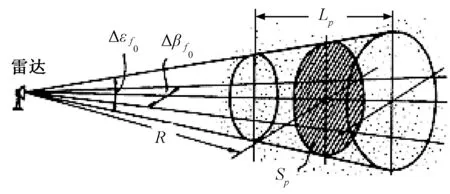
圖2 艦載雷達波束覆蓋的空域

根據圖2，可以求出：

vp=LpSp

(13)

且有：

(14)

(15)

式中：Δβf0為電平為f0的水平波束寬度；Δεf0為電平為f0的垂直波束寬度；τn為艦載雷達脈沖寬度；c為光速。

依據式(12)～(15)可以獲得：

(16)

此外，對于對稱天線波束來講，其增益為：

(17)

將式(16)和(17)代入式(11)，便可獲得艦載雷達接收機輸入端無源干擾平均功率，即：

(18)

2.3 無源干擾下的雷達發現效能概率

由式(18)可以看出，無源干擾功率與雷達作用距離的4次方成反比，利用式(18)即可獲得無源干擾條件下艦載雷達的發現距離：

(19)

3 結束語

本文在理論上給出了復雜電磁環境中無源干擾對雷達效能的影響模型，從模型中可以看出，無源干擾所反映的功率越大，則雷達發現效能概率就越低；無源干擾的起伏越復雜，則雷達發現效能就越差。當然，為了進一步定量分析其影響程度，還可作進一步的仿真計算。