基于離散元法的雙臥軸攪拌機工作性能的分析與研究

張 宏

（山西省晉中路橋建設集團有限公司，山西 晉中 614000）

水泥混凝土、瀝青混凝土等攪拌設備的性能與研究進展，在很大程度上影響了道路、橋梁、房屋等建筑與基礎設施的安全性與使用壽命，因此對相關攪拌設備開展研究，通過改變其運動參數(shù)與幾何參數(shù)，從而提高攪拌的均勻性變得尤為重要［1］。但目前已有的研究方法存在較大的局限性，不能完全滿足并符合實際攪拌的工作要求［2］。

離散元法是用來解決不連續(xù)介質問題的數(shù)值模擬方法，其基本思想是把散體群粒簡化成一個具有質量和形狀的顆粒的集合，被廣泛應用于道路建設、農(nóng)業(yè)工程等行業(yè)［3-5］。蔡改貧等［6］通過離散元法研究了巖石在受到?jīng)_擊進行破碎的情況下的受力與裂紋出現(xiàn)、延伸的關系，解釋了顆粒體破碎的微觀過程。李建生［7］應用離散元軟件EDEM得到了立軸式破碎機喂料環(huán)角度、轉子與喂料盤高度對破碎處理量的關系。王家全等［8］采用EDEM軟件分析了土工格柵在新舊路堤的受力分布，以及加筋區(qū)域土體細觀參數(shù)的變化。離散率為攪拌均勻性能的最主要評價指標，客觀反映了單位體積內顆粒的均勻程度，其值越小則攪拌性能越好，反之則越差。本文以“JS3000”型號雙臥軸攪拌機為研究載體，對其攪拌過程進行研究分析，在此基礎上，以離散率為攪拌均勻性能的評價指標，運用離散元軟件EDEM作二次正交旋轉組合試驗，旨在利用一定的計算方法獲得攪拌機的最優(yōu)參數(shù)組合，為攪拌機的優(yōu)化提供理論依據(jù)，促進建筑行業(yè)與筑路行業(yè)的發(fā)展。

1 模型的建立

1.1 離散元算法計算流程

在離散元法的研究中，若顆粒間表面沒有黏附作用，設置顆粒與幾何體、顆粒與顆粒之間的接觸模型為Hertz-Mindlin（no slip）built-in［9］。其計算程序流程如圖1。

圖1 離散元法計算流程

1.2 攪拌過程模型

將攪拌過程中不同顆粒含量的變化視為隨機的馬爾柯夫過程，使得攪拌過程可以采用柯爾莫高洛夫微分-差分方程表達［10］，即

式中：Nf為時間為t1，攪拌機內某成分結合數(shù)量的隨機值；PNb（t）為隨機取值Nf取整數(shù)值Nb的概率，即PNb＝p｛Nf（t）＝Nb｝；γNb為常數(shù)。

對于圓柱殼體攪拌機（圖2）的攪拌過程，可以采用柯爾莫高洛夫方程模擬攪拌動態(tài)變化過程的擴散過程，即

式中：M為攪拌物中關鍵成分的含量（kg）；t為攪拌時間（s）；v為攪拌物的軸向速度（m／s）；c1、c2分別為攪拌物的軸向、徑向擴散系數(shù)；l、r分別為攪拌機內腔的軸向與徑向坐標，軸向、徑向擴散系數(shù)的大小主要取決于顆粒尺寸、充盈率以及攪拌速度等。但除上述攪拌過程的分析之外，混凝土等屬黏-塑混合物，且攪拌軸上的葉片運動破壞了顆粒行為的連續(xù)性，因此混凝土的離散率與其內部運動受多因素影響。本研究通過改變充盈率、攪拌軸轉速、葉片安裝角等參數(shù)，間接影響離散率。

圖2 攪拌機模型簡圖

2 基于EDEM 的輔助參數(shù)設計和優(yōu)化

通過前述對攪拌工作過程的分析，為優(yōu)化攪拌機的結構參數(shù)和運動參數(shù)，提高其性能，選取攪拌軸轉速、充盈率、葉片安裝角3個因素進行仿真試驗。試驗采用二次回歸正交旋轉組合設計。

2.1 顆粒模型及幾何模型的建立

攪拌機中水泥、砂子、碎石的幾何尺寸等為隨機變量，同樣是影響攪拌性能的主要因素。本研究以礦渣硅酸鹽水泥、粗砂、石子為研究對象，采用落料試驗（圖3）測得不同顆粒塌落后的休止角，通過離散元公司所提供相關網(wǎng)站輸入不同顆粒休止角獲得其部分物理特性與力學特性［11］。對華中科技大學所購買某廠家所產(chǎn)的雙臥軸攪拌機（圖4）進行測量，并建立其三維模型，由于在離散元仿真模擬中只需將與顆粒接觸的幾何部件導入，所以將雙臥軸攪拌機模型進行簡化，應用三維軟件UG對其建模，如圖5所示。

圖3 落料試驗裝置

圖4 雙臥軸攪拌機

圖5 雙臥軸攪拌機仿真模型

2.2 EDEM 軟件仿真

根據(jù)文獻、測試結果及材料庫，水泥、砂子、碎石顆粒以及雙臥軸攪拌機的物理特性和相互間的力學特性如表1（其中密度為測試結果，泊松比與剪切模量由已有文獻得出）、表2所示［12-14］。

表1 仿真物理特性

表2 仿真學特性

由于砂子、碎石顆粒表面無黏附作用，加之前文對離散元模型的研究得知選擇Hertz-MindLin（no slip）built-in為仿真接觸模型。但水泥具有黏結的特性，且EDEM中的JKR模型適用于具有黏結作用的仿真，因此通過API接口對該接觸模型進行二次開發(fā)［15］。命令水泥的接觸模型為編譯后的JKR模型，其余接觸模型為Hertz-MindLin（no slip）built-in。本研究以混凝土強度等級為C25的配比為依據(jù)，同時為了保證仿真時雙臥軸攪拌機工作有足夠的顆粒和仿真時間，設置生成水泥顆粒數(shù)、砂子顆粒、碎石顆粒目分別為90 000、32 000、17 000［16］，半徑平均值為1、7、23 mm，采用正態(tài)分布的方式生成顆粒尺寸，標準差分別為0.086、0.102、0.093，同時對不同顆粒進行不同顏色的著色，設置固定時間步長為Rayleigth時間步長20%，仿真時間共31 s，前7 s為顆粒工廠生成各類顆粒的時間。同時為計算反映攪拌均勻性的離散率，對該雙臥軸攪拌機進行網(wǎng)格劃分，如圖6所示。

圖6 網(wǎng)格劃分

2.3 仿真試驗因素與指標

本研究臥軸攪拌機的工作性能評價指標為離散率（L），該值越大，攪拌效果越不均勻，反之則攪拌效果越均勻［17］。均勻度的離散率的求解過程為：令臥軸攪拌機內3種顆粒數(shù)目分別Nd、Ne、Nf，攪拌機內顆粒總數(shù)目為N＝Nd＋Ne＋Nf。同理，每個網(wǎng)格中顆粒總數(shù)目與3種顆粒數(shù)目分別為n、nd、ne、nf，實際與理想狀態(tài)下顆粒的均勻程度偏離程度總偏離程度為

式中j為仿真中網(wǎng)格的總數(shù)目，則均勻度離散率L為

根據(jù)前述理論分析及臥軸攪拌機作業(yè)要求，合理地控制試驗因素變化范圍，每號試驗重復9次，取其平均值作為試驗結果，因素水平編碼如表3所示，試驗方案與結果如表4所示。

表3 因素水平編碼

表4 試驗方案與結果

2.4 試驗結果及分析

2.4.1 離散率

運用spss數(shù)據(jù)分析軟件對表4離散率試驗結果進行回歸分析，其回歸方程檢驗數(shù)據(jù)如表5所示。

表5 離散率回歸方程檢驗表

查F表得F0.01（10，13）＝4.10，F(xiàn)＝173.619＞F0.01（10，13），因此回歸方程高度顯著，其二次回歸方程模型為

運用Matlab繪制三維等值線圖，如圖7所示。分析圖7可以得知，將充盈率固定在零水平時，隨著攪拌軸轉速的增大，離散率呈現(xiàn)先下降后上升的趨勢，這主要是由于當轉速較低時，顆粒運動的循環(huán)次數(shù)較低，攪拌不均勻，因此其離散率較大。但當轉速增大到一定數(shù)值時，攪拌機內顆粒具有較大離心力，從而同樣破壞其均勻性，造成離散率增大。將攪拌軸轉速固定在零水平時，出現(xiàn)了隨著充盈率的增加，離散率先下降后上升的現(xiàn)象，這主要是因為當攪拌機內充盈率較低時，相互作用的顆粒很少，減小了顆粒之間的摩擦力，不能形成大范圍內的運動，從而造成了離散率的增大。但隨著充盈率增大，當其超過一定數(shù)值時，攪拌機內部留給顆粒運動的空間過小，減小了顆粒整體的沸騰作用，同樣出現(xiàn)了攪拌不均勻，造成了離散率的增加。另外，將葉片安裝角固定在零水平時，隨著攪拌軸轉速的增加，離散率出現(xiàn)了先下降后上升，而將攪拌軸轉速固定在零水平時，葉片安裝角的增加對離散率的影響不大。將葉片安裝角固定在零水平時，隨著充盈率的增加，離散率出現(xiàn)了先下降后上升，而將充盈率速固定在零水平時，葉片安裝角增加對離散率的影響不大。除此之外，由回歸方程和三維等值線圖可知，在試驗范圍內三因素對雙臥軸攪拌機離散率顯著性影響大小順序是充盈率、攪拌軸轉速、葉片安裝角。

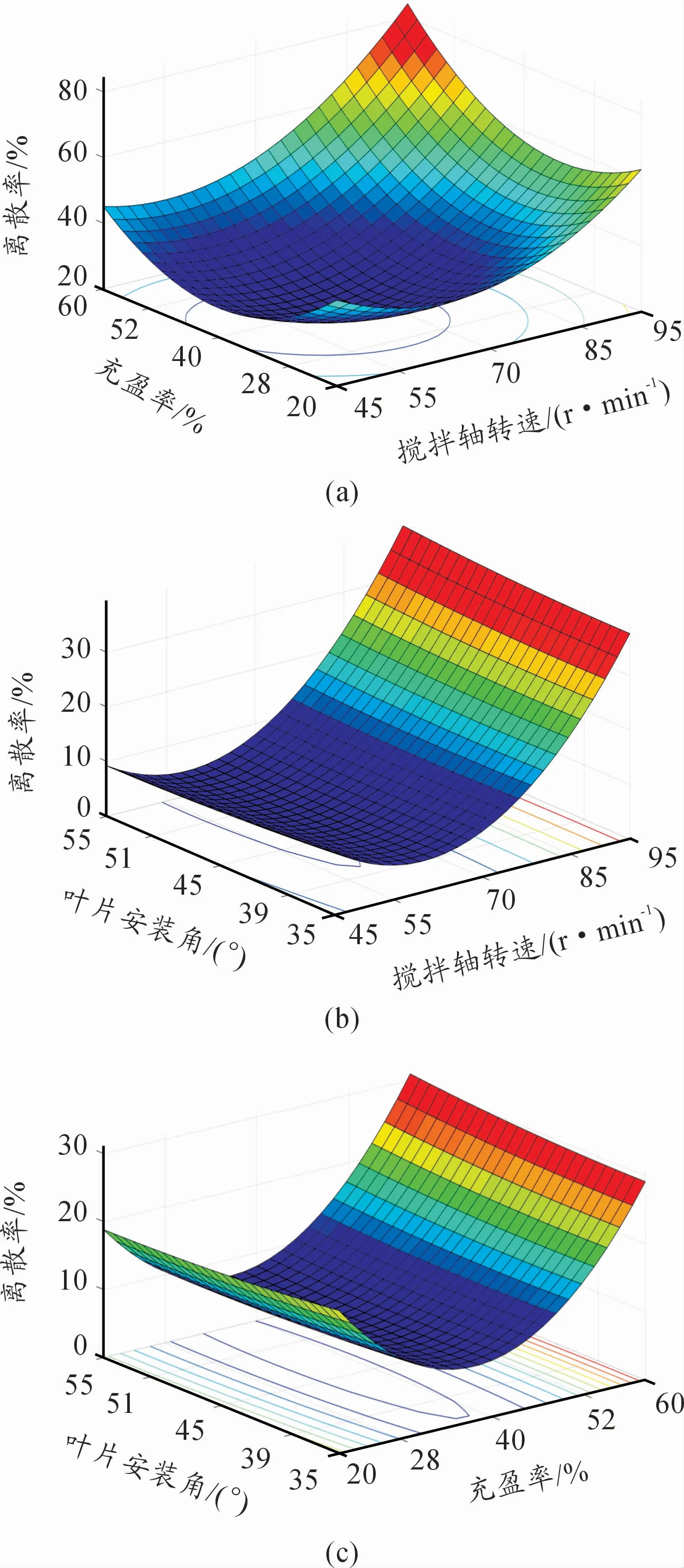
圖7 離散率等值線圖

2.4.2 雙臥軸攪拌機性能優(yōu)化

根據(jù)優(yōu)化數(shù)學模型和攪拌機各性能評價指標的回歸方程，利用Matlab中非線性優(yōu)化fmincon函數(shù)，以F（max）＝L即離散率最小為條件進行尋優(yōu)處理。優(yōu)化處理結果為：取攪拌軸轉速為61.93 r／min，充盈率為38.02%，葉片安裝角為46.34°。在此條件下進行仿真驗證試驗，試驗表明雙臥軸攪拌機離散率為6.22%。

3 試驗驗證

為驗證離散元軟件EDEM 研究結果的可行性，在華中科技大學土木工程與力學學院工程結構分析與安全評定湖北省重點實驗室開展試驗驗證。在充盈率為40%，葉片安裝角為35°、39°、45°、51°、55°的情況下，使用變頻器令攪拌軸轉速分別45、55、70、85、95 r／min，用混凝土多功能無損檢測儀SCE-MATS（圖8）對不同轉速下的離散率進行測定。試驗與仿真結果如圖9所示。

圖8 SCE-MATS型混凝土多功能無損檢測儀

圖9 不同轉速下試驗與仿真的顆粒離散率對比

從圖9可以看出，在不同葉片安裝角角度下，隨著轉速的增加，試驗與仿真的離散率變化趨勢基本一致，試驗所得離散率略大于仿真所得離散率。造成該現(xiàn)象的主要原因有：試驗中葉片傾角的加工存在誤差，無法完全達到設定值。除此之外，由于傳動過程中摩擦等原因，造成了試驗攪拌軸轉速與設定值的偏差。當轉速低于70 r／minj時，離散率波動較小，試驗所得離散率與仿真所得離散率差異較小；當轉速高于70 r／min時，離散率波動較大，試驗所得離散率與仿真所得離散率差異較大，其中最大差值為5.07%。仿真分析結果與試驗結果吻合，證明了采用離散元法研究雙臥軸攪拌機工作性能、攪拌均勻性的可行性。

4 結論

1）運用EDEM作正交攪拌虛擬試驗，通過二次回歸正交旋轉組合試驗建立了以離散率為考察指標的回歸方程。運用Matlab繪制離散率的等值線圖，得到在試驗范圍內三因素對離散率顯著性影響大小的順序是充盈率、攪拌軸轉速、葉片安裝角。

2）確定了該型雙臥軸攪拌機的最佳參數(shù)組合，當攪拌軸轉速為61.93 r／min，充盈率為38.02%，葉片安裝角為46.34°時，攪拌最均勻，此時雙臥軸攪拌機離散率為6.22%。

3）通過不同葉片安裝角、不同轉速下離散率的仿真與試驗結果對比，得知兩者結果變化趨勢一致，結果基本相同。