高速鐵路(110+208+110) m連續梁-鋼管混凝土拱屈曲分析

司萬勝

(中鐵第一勘察設計院集團有限公司,西安 710043)

1 概述

連續梁-鋼管混凝土拱組合結構橋因其施工適應性強、結構動力特性優良及工后變形易于控制等優點，成為高速鐵路120～220 m跨度橋梁方案比選中的新秀。基于統一理論本構模型的鋼管混凝土拱肋彈性及彈塑性屈曲分析，探索鋼管混凝土拱肋考慮鋼管和混凝土相互作用效應、核心混凝土脫空及鋼管初應力效應后彈性屈曲因子與彈塑性屈曲因子之間的關系，為鐵路鋼管混凝土拱橋采用統一理論模型進行結構穩定性分析提供參考。

2 鋼管混凝土結構

鋼管混凝土結構是以鋼管內填充混凝土為主要受力構件的結構，主要分為實心和空心鋼管混凝土。截面多為矩形、圓形和多邊形，其中圓形截面以其均勻的應力分布和優異的約束效應在此類構件應用中獨占鰲頭。采用自密實補償收縮混凝土作為核心混凝土，很大程度上減小了脫空率對結構承載力的削弱。本文所討論的均指圓形截面實心鋼管混凝土結構或構件。

2.1 發展歷史

鋼管混凝土結構最早出現在1879年英國修建的Seven橋[1]上，當時主要是為了防止鋼管內壁銹蝕，后來在歐美國家的工業與民用建筑領域被采用，但由于人工澆筑核心混凝土工作強度大、造價高，鋼管混凝土在發達國家的應用和發展曾一度停滯不前，直到20世紀80年代泵送混凝土技術的出現才讓其發展重獲生機。期間日本修建的許多鋼管混凝土結構在多次大地震中經受住了嚴峻考驗，其優良的抗震性能使得國際工程界再次將研究目光投向這種復合材料。真正的鋼管混凝土拱橋最早出現在1930年前蘇聯列寧格勒涅瓦河大橋[2]上，1990年修建的四川旺蒼東河大橋[3]是我國修建最早的鋼管混凝土拱橋，目前國內已建成鋼管混凝土拱橋300多座。

2.2 材料模型

作為鋼管和混凝土組合而成的材料，鋼管混凝土構件在結構分析中的模擬方式對結構分析有很大影響，目前各國學者[4]在計算機有限元分析中對鋼管混凝土構件的單元模擬主要有雙單元模型、纖維單元模型、換算材料模型以及統一理論模型。研究表明，鋼管和核心混凝土的相互作用效應[5-6]、核心混凝土脫空[7]以及與施工方案有關的鋼管初應力[8]很大程度地影響著鋼管混凝土結構承載能力。在計算機數值分析技術高度發達的今天，雙單元模型因過程繁瑣且無法有效模擬鋼管和混凝土之間的相互作用這一關鍵特征，已無法適應結構精細化設計的要求。目前國內已頒布了關于鋼管混凝土結構設計的最新國家標準[9-10]及行業標準[11]，國家標準采用換算鋼管(或混凝土)單材料模型，考慮到結構構件使用環境及受力差異，國家標準[9]在計算組合截面抗彎剛度時對核心混凝土剛度有所折減；公路行業標準則采用統一理論模型。國家標準[9]和行業標準[11]對影響鋼管混凝土構件承載力和穩定的約束效應、脫空及初應力均有比較周全的考慮。

2.3 鐵路鋼管混凝土拱橋設計現狀

國內第一座鐵路鋼管混凝土拱橋—貴州水柏鐵路北盤江大橋[12]自2002年8月通車運營至今已有十多年，期間鋼管混凝土拱橋以其獨特優勢在鐵路橋梁建設中得到快速發展，然而卻沒有基于鐵路行業標準的鋼管混凝土拱橋相關規范，雖然國內也有不少學者和工程設計者[13-15]結合實際工程對鐵路鋼管混凝土拱橋設計和施工進行了研究和總結，但限于鐵路行業鋼管混凝土拱橋設計無規可依的現狀，許多設計者難免陷入茫然。

3 穩定理論及分析

結構穩定問題源于1744年歐拉對理想中心壓桿彈性屈曲臨界力的研究。結構失穩是指在外力作用下結構平衡狀態開始喪失穩定性，稍有擾動(實際不可避免)則變形迅速增大，最后結構破壞。穩定性問題在橋梁、船舶、飛機等工程領域普遍存在，隨著高強材料的運用，屈曲分析在結構設計中的重要性越來越突出。國外學者[16]對桿、板、殼各類結構構件的彈性和彈塑性屈曲進行了詳細論述。李國豪教授[17]就橋梁結構穩定和屈曲進行了有針對性的深入研究。普遍認為[18-19]橋梁結構失穩主要分為兩種類型。

3.1 第一類分支點失穩

分支點失穩主要指當結構外荷載達到其臨界荷載時，除結構原有平衡狀態外尚存在其他平衡狀態，也即出現平衡分支。分支點失穩在結構穩定性分析中對應著彈性屈曲分析，因為其力學求解在數學上可歸結為特征值求解，也稱之為特征值屈曲分析，彈性屈曲針對理想材料結構，不包含任何非線性因素。

3.2 第二類極值點失穩

極值點失穩是指結構在外荷載作用下保持著一個平衡狀態(一般是彈性屈曲分析中的一階屈曲模態)，隨著外荷載增加，當結構應力較大區域的應力大于材料比例極限時發生塑性變形，結構變形快速增大，當荷載增大到某一數值時，即便荷載維持不變，變形也繼續自行急劇增大直至結構破壞，這個最終導致結構破壞的荷載稱之為極限荷載。極值點失穩在結構穩定性分析中對應著彈塑性屈曲分析，也稱之為全過程屈曲分析，一般用于求解結構的極限承載力。

除了上述第一和第二類穩定外，還有一種結構失穩即跳躍失穩[20]。這種失穩主要指處于某一平衡狀態的薄殼在微小擾動下突然轉入另一種平衡狀態，平衡狀態的轉變具有突變性，這種失穩主要存在于球面網殼類結構中，橋梁結構穩定分析一般不研究。

3.3 鋼管混凝土拱橋穩定分析

關于鋼管混凝土拱肋穩定，現行國家標準[9]以及公路行業標準[11]和鐵路行業標準[21]均提出了其彈性穩定系數不小于4.0的具體要求。然而，現代拱橋隨著跨度增大，拱肋穩定問題也越來越突出，拱橋穩定研究僅停留在彈性屈曲分析的層面，顯然遠不能滿足設計需求。基于滿足一定約束效應條件的鋼管和核心混凝土之間的相互作用，鋼管混凝土拱的承載能力相較于等效鋼筋混凝土勁性骨架拱有顯著提高，在最大限度滿足承載力的條件下，拱肋截面更趨纖細，有設計者在缺乏彈塑性屈曲分析而拱肋承載力又不控制的情況下，通過增加拱肋弦管管徑等方法將彈性屈曲因子提高，彈性屈曲因子甚至有高達10以上者，這種做法實不可取。公路行業標準[11]對大跨度拱的穩定性分析，提出了考慮幾何-材料雙重非線性因素時其穩定系數不小于1.75的要求，鐵路鋼管混凝土拱橋設計可參考采用。

4 結構模型簡介

高速鐵路(110+208+110) m連續梁-鋼管混凝土拱組合橋采用先梁后拱施工方案：先懸臂澆筑并合龍混凝土連續梁，然后以混凝土橋面為施工作業平臺現場拼裝預制空心鋼管拱肋，最后泵送頂升灌注管內自密實補償收縮核心混凝土。連續梁采用單箱雙室二次拋物線變高截面，邊支點及跨中梁高4.0 m，中支點梁高11.0 m，箱梁頂寬16.5 m，箱寬14.0 m；吊索采用OVM·GJ15-15整束擠壓鋼絞線，順橋間距8.0 m，橫橋間距15.0 m，全橋共23對；啞鈴形拱肋截面高度3.5 m，弦管規格φ1 300×28 mm；橫撐主管和支管分別采用4肢和雙肢格構式，鋼管規格均為φ500×12 mm，上下肢中心高2.2 m，左右肢中心寬2.2 m，拱頂設置1道“一”撐、兩側各設5道“K”撐，全橋共11道支撐。模型中鋼管混凝土拱肋采用統一理論模擬，吊索鋼絞線采用桁架單元模擬。混凝土連續梁和拱肋鋼管分別采用C55混凝土和Q345qE鋼，全橋模型見圖1。

圖1 全橋模型

5 屈曲分析

對模型鋼管混凝土拱肋運營階段進行彈性屈曲、幾何非線性屈曲和材料非線性屈曲分析，全面了解恒載、橫向風載及全跨ZK活載作用下結構屈曲特征。

5.1 彈性屈曲分析

雖然彈性屈曲分析對象是理想彈性和無缺陷結構，但其分析所得的屈曲模態有助于設計者對結構特性的宏觀理解和把握，其臨界荷載近似代表了相應極值點失穩的極限荷載上限值。就此而言，彈性屈曲分析作為結構穩定分析設計的基礎性工作，其重要性不言而喻。

5.1.1 屈曲模態

彈性屈曲分析結果顯示，對于大跨度拱，拱肋失穩方向主要發生在橫橋向，即面外失穩。提取鋼管混凝土拱肋前5階屈曲模態見圖2。

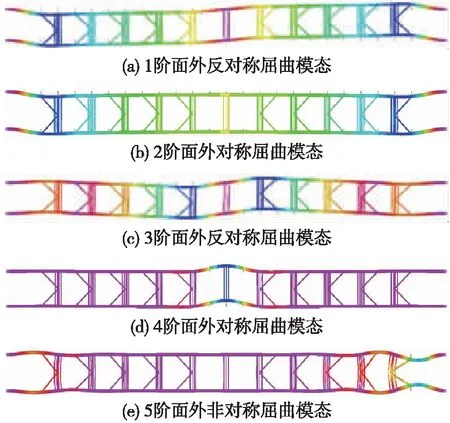
圖2 彈性屈曲模態

5.1.2 模態描述

鋼管混凝土拱肋前5階屈曲模態描述見表1。

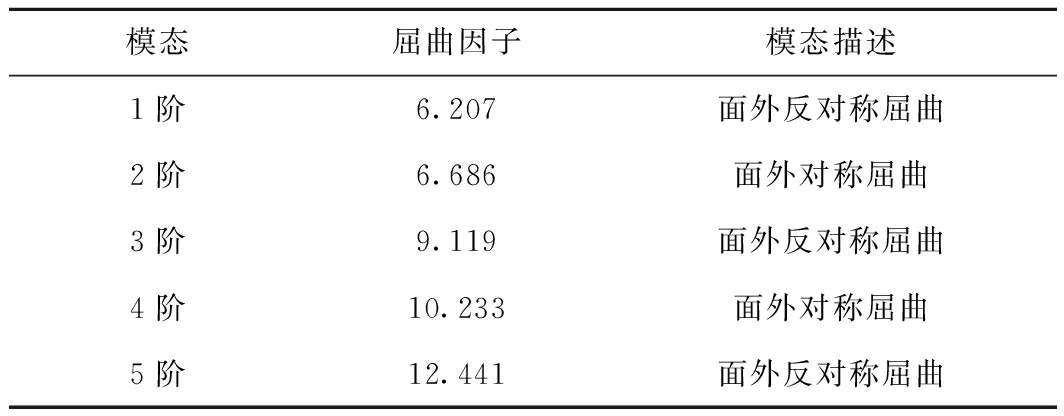
表1 彈性屈曲分析

5.2 幾何非線性屈曲分析

彈塑性屈曲分析中結構初始幾何缺陷的引入，建工網格規程[22]按結構低階屈曲模態考慮并限制缺陷最大值，而公路及鐵路橋涵設計規范均無此項規定，建議拱橋彈塑性屈曲分析時根據結構彈性屈曲分析的低階(一般是1階)模態引入初始幾何缺陷，缺陷引入值宜為拱肋跨度的1/1 000～1/800。模型引入面外初始幾何缺陷激發低階屈曲并考慮大變形效應后承載力曲線見圖3。

圖3 幾何非線性位移-承載力曲線

圖3中橫坐標為監測點低階模態屈曲方向位移，縱坐標為豎向承載力值。曲線顯示，監測位移接近1.0 m時承載力基本不再增大，此時最大承載力約為4.702×106kN。

5.3 幾何-材料非線性屈曲分析

目前結構彈塑性分析的非線性行為大多通過在結構上指定離散的、具有非線性屬性的鉸行為來實現，橋梁結構分析通常指定塑性鉸或纖維鉸。國內規范對相關材料塑性鉸的骨架曲線、容許準則和滯回類型等鉸屬性并無定義，塑性鉸屬性定義多采用ASCE41、FEMA441及ATC40等美國標準，然而對鋼管混凝土拱肋指定耦合的P-M-M塑性鉸尚需要相關面數據支持，為避免建立這些支持數據繁重而艱巨的工作，模型采用統一理論定義鋼管混凝土本構關系并指定組合材料纖維鉸，可以取得較為理想的結構分析結果。

5.3.1 鋼管混凝土統一理論

鋼管混凝土材料應力-應變本構關系的統一理論模型改變了傳統鋼管混凝土結構分析時換算材料建模或分材料建模，將鋼管混凝土視為鋼管和混凝土組合而成的統一體新材料來研究其組合性能，研究成果表明[23]，鋼管混凝土組合材料的工作性能具有統一性、連續性和相關性。本例模型根據統一理論和截面幾何特征及材料物理特性，將鋼管混凝土應力-應變本構關系曲線按照彈性、彈塑性和強化3個階段進行合理簡化，建立三折線本構模型，本構關系曲線見圖4。

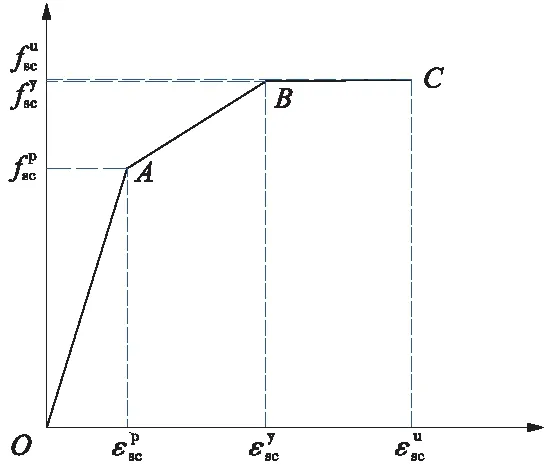
圖4 鋼管混凝土軸壓本構曲線

圖4中參數如下所示

5.3.2 承載力曲線

考慮幾何-材料雙重非線性后鋼管混凝土拱肋屈曲承載力曲線見圖5。

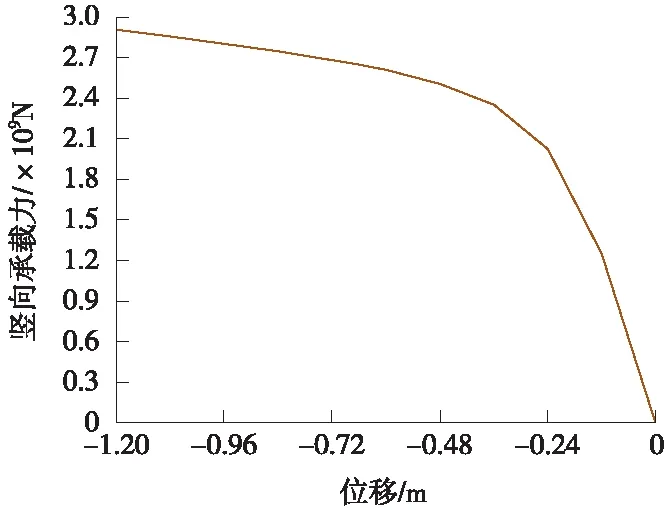
圖5 雙重非線性位移-承載力曲線

圖5中橫坐標為監測點低階模態屈曲方向位移，縱坐標為豎向承載力，考慮雙重非線性時最大豎向承載力約為2.870×106kN。

5.4 屈曲因子分析

限于篇幅，結構靜力分析不再贅述，直接引用其豎向承載力分析值Ncr=834 610 kN。通過以上闡述，提取1階彈性屈曲分析的屈曲因子和彈塑性屈曲分析的豎向承載力并換算彈塑性屈曲分析的換算屈曲因子，見表2。

表2 屈曲因子分析

表2的計算表明：相對于彈性屈曲因子，幾何非線性屈曲因子約占其91%，而幾何-材料雙重非線性屈曲因子約占其55%，并且材料非線性對結構屈曲的影響比幾何非線性對結構屈曲的影響要大得多，但參考公路行業標準[11]考慮雙重非線性后鋼管混凝土拱肋彈塑性穩定系數不小于1.75的要求，橋式方案的拱肋穩定性完全滿足要求并有相當余量，在拱肋承載力和變形滿足要求的前提下可對鋼管管徑和壁厚進一步優化。

6 結語

采用統一理論進行鋼管混凝土拱肋彈性及彈塑性屈曲分析時，在材料屬性中考慮鋼管和混凝土相互作用效應的方法更方便有效，分析結果吻合結構工程力學行為。屈曲分析表明，材料非線性對鋼管混凝土拱肋屈曲影響很大，考慮雙重非線性的結構彈塑性屈曲因子相對于彈性屈曲因子大幅衰減，但其穩定性仍然滿足規范要求。因此，在沒有特殊需求的情況下，對于國家標準和各行業標準提出的鋼管混凝土拱橋拱肋彈性穩定系數不小于4.0的要求，不宜太過保守地提高，以免出現拱肋尺寸過大，造成梁拱結合部構造處理困難及過大的梁部構造尺寸，從而導致結構設計不合理且浪費材料。