基于裝配機械彈性車輪的車輛平順性的油氣懸架優化研究

趙又群，葉 超，白毅強

（南京航空航天大學，南京 210016）

為使車輛適應惡劣的行駛環境，其平順性及操縱穩定性的改善具有十分重要的意義。本課題組研究的一種機械彈性車輪，由于擁有較大的側偏剛度，能增強車輛在復雜路面下的操縱穩定性［1］，但由于其大徑向剛度特性導致了平順性的不足［2-3］。為保證該種車輪的實際應用效果，需要進行懸架優化。而油氣懸架的非線性剛度與阻尼特性能較好地改善車輛的平順性，被廣泛地用于越野車、高級轎車以及工程、軍事車輛中［4］。二者的結合對提升車輛性能意義重大。

油氣懸架的各項參數對其性能有著復雜的影響，傳統優化算法難以勝任。隨著優化算法的發展，群智能優化算法由于能處理多變量多目標的優化問題逐漸在工程優化上得到普及。目前國內外相關學者對于油氣懸架的非線性特性［5］、結構設計［6-7］以及半主動控制［8-9］等方面研究已經做了大量工作，但對于油氣懸架的設計參數優化的相關資料較少［10-12］。對于多目標、多參數的油氣懸架優化算法的選取以及針對不同車輛參數及環境的優化效果仍需要進一步的研究。

本文以某越野車為例，建立了包含機械彈性車輪與油氣懸架的半車模型，在此基礎上，以提升平順性為優化目標確定優化參數，利用量子遺傳算法對油氣懸架參數進行了多目標、多參數的優化設計，并對優化結果進行了分析。

1 機械彈性車輪

本文所采用的機械彈性車輪結構如圖1所示。該車輪主要由輪轂、車輪外圈及連接二者的12個鉸鏈組組成。經仿真分析與實車實驗研究后，得知其擁有的大側偏剛度保證了車輛的操縱穩定性，但是其相對于子午線車輪較大的徑向剛度會對車輛的平順性產生不利影響［2］。

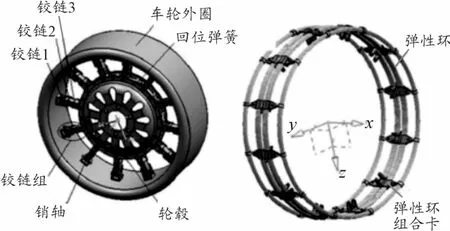
圖1 機械彈性車輪結構示意圖

已有的研究中，課題組使用輪胎特性靜載試驗臺對車輪的徑向剛度進行了測量，并在Adams中建立了車輪的有限元模型對其徑向剛度進行仿真，得到車輪的靜載徑向剛度為630 390 N／m，其值約為普通子午線輪胎的2倍［13］。為簡化問題，不失一般性，本文取該剛度進行研究。

2 車輛平順性仿真模型

2.1 單筒式油氣彈簧

油氣彈簧是在膜式空氣彈簧的基礎上發展而來的，是油氣懸架的核心部件。本文所研究的一種單筒式油氣彈簧的結構示意圖如圖2所示［14］，它將氣室置于活塞桿內部，使得結構更加緊湊。其工作原理是通過氣室內的惰性氣體的壓縮與膨脹緩和沖擊，通過活塞與油腔內的油液流動衰減振動。

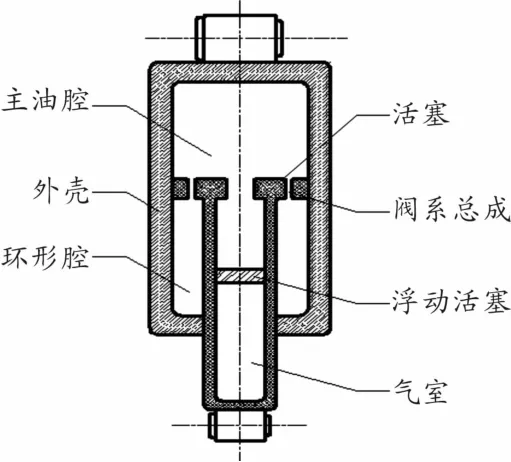
圖2 油氣彈簧結構示意圖

油氣彈簧的彈性力主要由氣室內的惰性氣體的狀態變化來提供，一般使用氮氣。依據理想氣體狀態方程可以得到，當活塞位移為x時，此時的彈性力為：

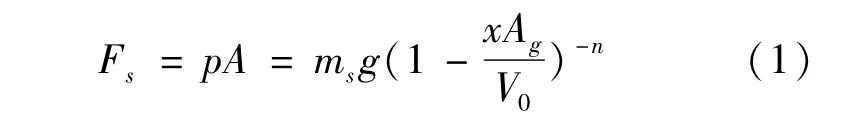
式中：p為活塞位移x時氣室內的壓強；Ag為活塞桿內腔截面積；ms為前懸架或后懸架的靜載質量；V0為初始充氣體積；n為氣體多變指數，油氣彈簧運動速度較快，氣室內氣體可近似視為絕熱狀態，這里取n＝1.4。

油氣彈簧的阻尼力主要由油液通過阻尼孔與單向閥在主油腔與環形腔之間流動來提供，單向閥僅在壓縮行程時打開。由小孔節流公式可以得到，當活塞速度為v時，此時的阻尼力為：

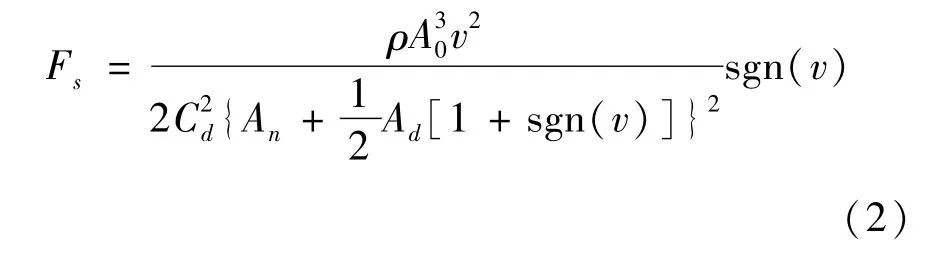
式中：Cd為小孔節流的流量系數，這里取 Cd＝0.68；ρ為油液密度；A0為環形腔橫截面積；An為等效阻尼孔面積；Ad為等效單向閥橫截面積。本文研究的油氣彈簧的初始參數如表1所示。

在Matlab／Simulink中建立該油氣彈簧的模型，得到的油氣懸架彈性力-位移曲線與阻尼力-速度曲線如圖3、4所示。該結果符合油氣懸架的非線性特性［5，11-12］，模型較好地完成了油氣懸架性能的模擬。

2.2 4自由度半車模型

為提高優化計算的效率，同時考慮車輛前后懸架的差異，本文通過建立一種4自由度半車模型對油氣懸架進行平順性優化［15］，其示意圖如圖5所示。

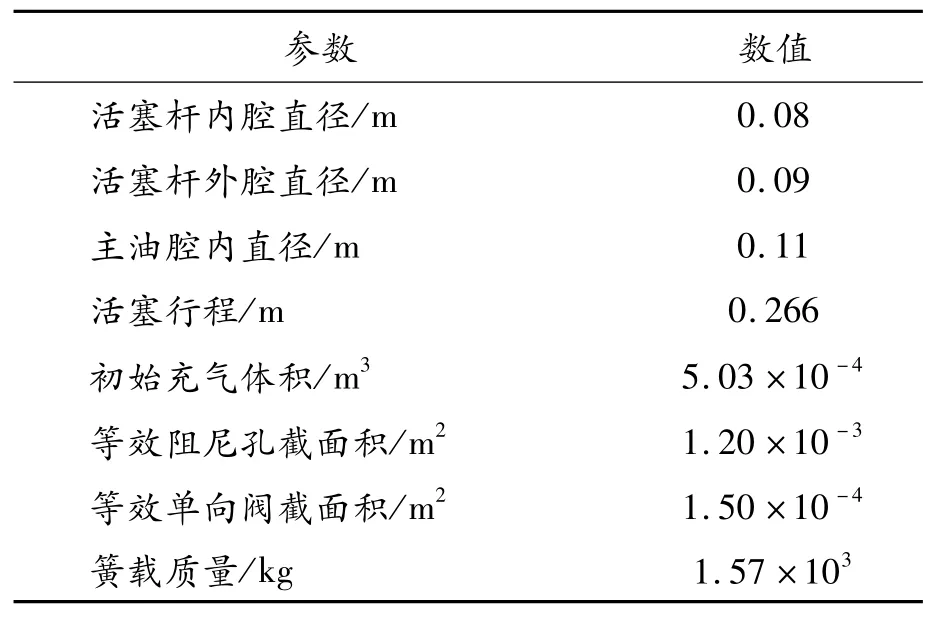
表1 油氣彈簧參數

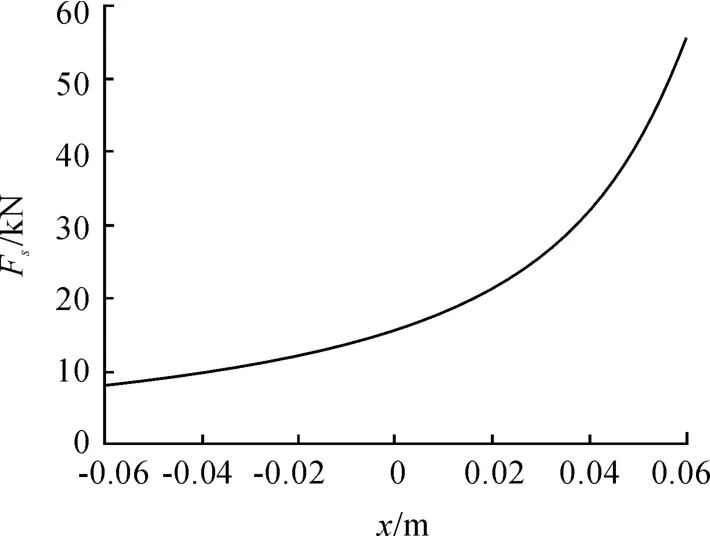
圖3 油氣懸架彈性力-位移曲線

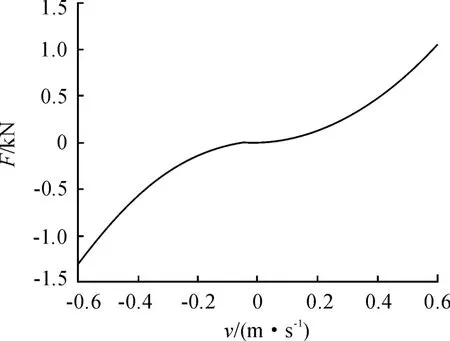
圖4 油氣懸架阻尼力-速度曲線

圖5 中：ms為簧載質量；Jφ為繞y軸的轉動慣量；φ為繞y軸的轉動角度；xc為質心豎直位移；L為軸距；b為前軸距；xs1、xs2分別為前后軸豎直位移；ks1、ks2分別為前后懸架剛度；cs1、cs2分別為前后懸架阻尼；mt1、mt2分別為前后簧下質量；xk1、xk2分別為前后簧下質量的豎直位移；kt1、kt2分別為前后車輪剛度；xr1、xr2分別為前后路面激勵。

圖5 4自由度半車模型

建立半車模型時使用的越野車參數如表2所示。

表2 越野車參數

2.3 路面白噪聲輸入

現階段主要采用路面的功率譜密度來描述研究車輛振動時路面不平度的統計特性［16］，路面的功率譜密度表達式為

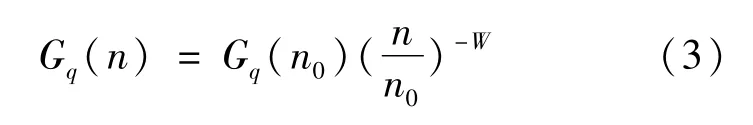
式中：n為空間頻率；n0為參考空間頻率，n0＝0.1；W為頻率指數；Gq（n0）為參考空間頻率下的路面不平度系數。本文在優化時以C級路面為研究對象，取 Gq（n0）＝256×10-6，車速設定為20 m／s。

2.4 車輛裝配機械彈性車輪與普通子午線輪胎的平順性對比

為驗證機械彈性車輪是否對車輛平順性造成負面影響，分別使用機械彈性車輪與普通子午線輪胎在不同等級路面下進行仿真實驗，這里采用的子午線輪胎徑向剛度為 320 450 N／m［13］，平順性指標為垂向振動與俯仰振動的加權加速度均方根值，實驗結果如表3所示。

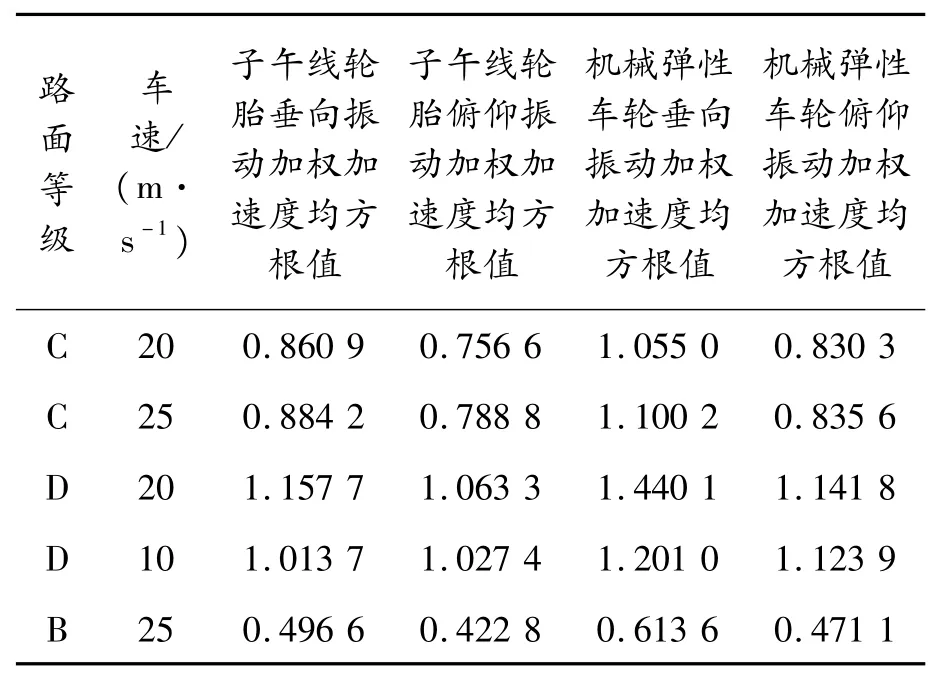
表3 機械彈性車輪與普通子午線輪胎在不同環境下的平順性指標

我國規定［16］，在評價車輛平順性時要考慮椅面x、y、z 3個方向（縱向、側向、垂向）的振動。這里做出如下假設：

1）假設座椅在車輛質心位置，且與車輛間沒有減震系統。

2）車輛加權加速度均方根值是3個方向的均方根值的加權和。由于車輛在x軸與y軸方向的振動加權加速度均方根在不平路面直線行駛時遠小于z軸方向，故忽略x軸與y軸方向的影響。

由實驗結果可知，在C級及以下等級路面上，普通子午線輪胎車輛的垂向加權加速度均方根值均小于 1，人的主觀感覺為“有一點不舒適”（0.315～0.63）到“不舒適”（0.5～1）之間。由于假設1忽略了座椅的減震性能，故實際給人的主觀感覺會更好，符合平順性的要求。在相同的車型、懸架的初始參數以及路面條件與車速下，裝配機械彈性車輪車輛的平順性要差于裝配子午線輪胎車輛，而油氣彈簧參數的可設計性使得該問題有望得到改善。

3 油氣懸架設計參數優化

3.1 量子遺傳算法

遺傳算法（genetic algorithm，GA）具有極高的魯棒性，被廣泛應用于各個領域的研究。但GA容易出現迭代次數多，或陷入局部極值等問題。因此研究者們對GA進行了一系列的改進［17-18］。

量子遺傳算法（quantum genetic algorithm，QGA）是一種將量子計算機與GA結合的概率進化算法。QGA將量子的態矢量表達引入遺傳編碼，利用量子邏輯門實現染色體的演化，由于采用量子比特編碼的染色體可以表達多個態的疊加，相較于常規GA具有更高的多樣性，不易陷入局部極值，且能更加逼近全局極值。QGA于1994年由Chor首先提出［19］，是一種新型智能優化算法，并在應用過程中不斷得到改進［20］，其已被用于信號處理、智能控制、TSP問題等領域，而工程設計方面的使用目前較少。

3.2 目標函數

質心的加權加速度均方根值是最常用的評價車輛平順性的指標，根據GB 7031—1987［21］規定，當振動的波形峰值系數小于9時，加權加速度均方根值的計算公式為

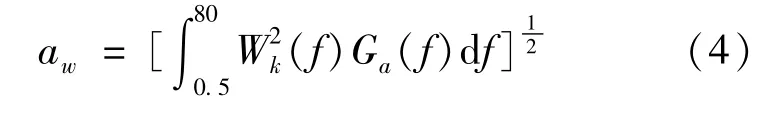
式中：Wk（f）為垂向振動頻率加權函數；Ga（f）為質心垂向振動加速度的功率譜密度。由此得到目標函數：

考慮車身的俯仰運動帶來的平順性問題，以俯仰角振動加權加速度均方根值來表示：

式中：We（f）為俯仰振動頻率加權函數；Gβ（f）為俯仰角振動加速度的功率譜密度。由此得到目標函數：

考慮到不平路面行駛過程中車輪與地面脫離的情況，需要對車輪的接地性進行優化。車輪的動載荷系數是常見的評價車輪接地性的指標，其物理意義為車輪動載荷均方根值與靜載荷之比，計算公式為：

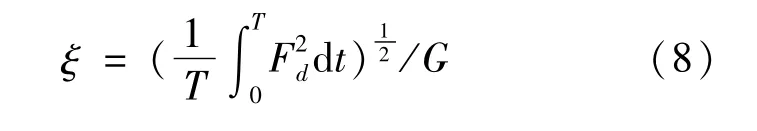
式中：Fd為車輪動載荷；G為車輪靜載荷。由此得到目標函數：

式中ξf、ξr分別為前后車輪動載荷系數。

目標函數J1、J2、J3、J4都要求盡可能小。

3.3 設計變量

影響油氣懸架性能的參數多且復雜，需兼顧優化效率與實際優化效果進行選取［22］。考慮到實際生產加工的統一，取活塞桿內腔面積Ag以及環形腔面積A0不變，并通過控制變量法研究其他參數對油氣彈簧性能的影響。圖6～8分別反映了初始充氣體積V0、等效阻尼孔面積An與等效單向閥面積Ad對油氣彈簧剛度與阻尼特性的影響。

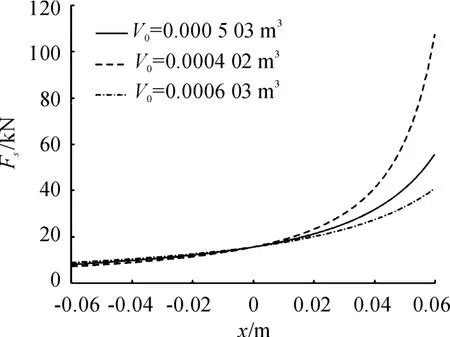
圖6 初始充氣體積對剛度的影響

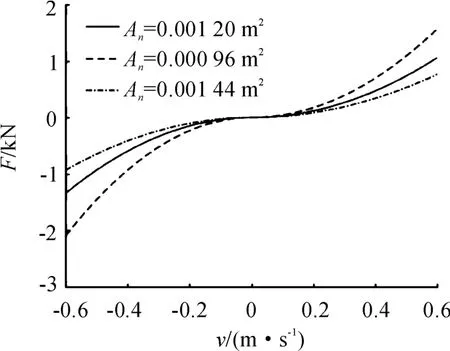
圖7 阻尼孔面積對阻尼的影響

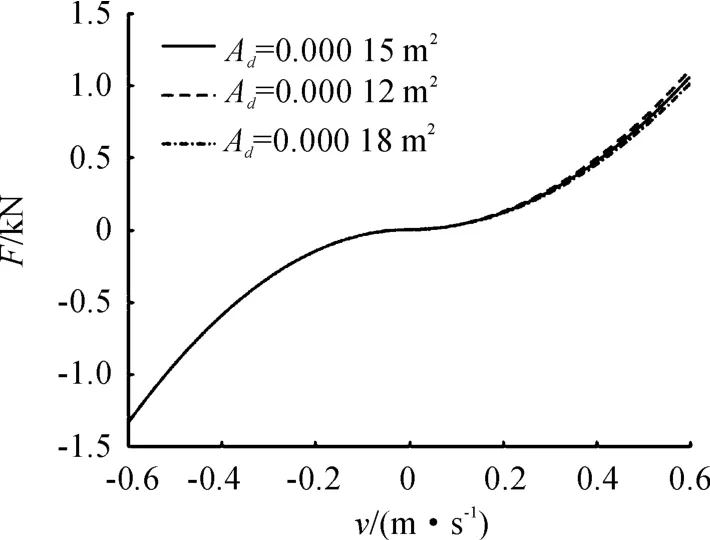
圖8 單向閥面積對阻尼的影響

通過仿真結果結合公式易看出，單向閥面積對阻尼特性的影響較小。考慮到油氣彈簧的單向閥結構相對復雜，為方便生產，前后彈簧采用相同尺寸的單向閥。綜上，可以確定設計變量分別為統一的等效單向閥面積、前后彈簧初始充氣體積、前后等效彈簧阻尼孔面積。

3.4 約束條件

3.4.1 邊界條件約束

邊界條件用于規定個體基因表達的范圍。

設計單向閥時需要考慮它與活塞的的相互布置位置。同時，由于是內置式氣室，故初始充氣體積應小于活塞桿內腔體積。由于使用了小孔節流公式，故等效阻尼孔面積的選取不能太大。

3.4.2 中間變量約束

中間變量以罰函數的形式在算法中表現約束力。

依據加速度均方根值與人的主觀感覺評定表，將加權加速度均方根值最大值awmax設定為1.25 m／s2。且一般認為，當車輪的動載荷系數低于1／3時，車輪跳離地面的概率在0.15%以下。當懸架的動行程S的均方根值低于懸架最大動行程Smax的1／3時，限位塊撞擊概率在0.3%以下。

3.5 數學模型

由此得到的油氣懸架優化的數學模型為：

使用表1所提供的初始參數進行計算［11］，得到的4個優化目標的初始值如表4所示。由初始結果可知，質心垂向加速度均方根值為1.055 0，此時人的主觀感覺為“相當不舒適”。為保證車輛平順性，需要對油氣懸架進行優化。

表4 各優化目標初始值

經過綜合分析，將4個優化目標的權重分別定義為：0.4、0.3、0.15、0.15。考慮到優化方便程度，可將4個優化目標加權相加得到一個整體優化目標，即：

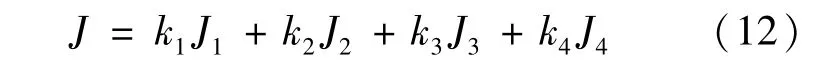
式中ki為第i個優化目標相對應的加權系數，這里采用初始值作為參考，其值按照式（13）計算。

3.6 優化參數選取

本文經過多次嘗試后確定的優化參數如表5所示。

表5 參數選取

4 優化結果分析

4.1 優化對比

為保證量子遺傳算法結果的可靠性，使用相同的初始參數進行了3次優化運算，優化結果如表6所示。

由表6可知，量子遺傳算法多次優化結果之間的差異性在1%左右，說明該算法較為穩定。選取其中綜合優化效果最好的第1次優化結果進行研究，其優化過程如圖9所示。由圖9可知：優化目標絕對值在剛開始計算的時候迅速下降，在100代左右達到最優值附近，并在之后趨于穩定。

表6 量子遺傳算法結果對比

圖9 量子遺傳算法進化過程

4.2 優化結果

由表6可知，第1次優化后，總的優化目標、垂向振動加權加速度均方根值、俯仰振動加權加速度均方根值、前后車輪動載荷分別改善了29.3%、21.3%、51.1%、23.5%、4.98%，越野車的平順性得到了較大幅度的提升。

優化前后的各參數參數如表7所示。

表7 優化前后油氣懸架各參數值

將表中數據代入模型中進行計算，得到優化前后質心垂向振動加速度、俯仰振動加速度、車輪載荷對比，如圖10～13所示。從圖中也可以看出，優化后車輛的平順性得到了改善。

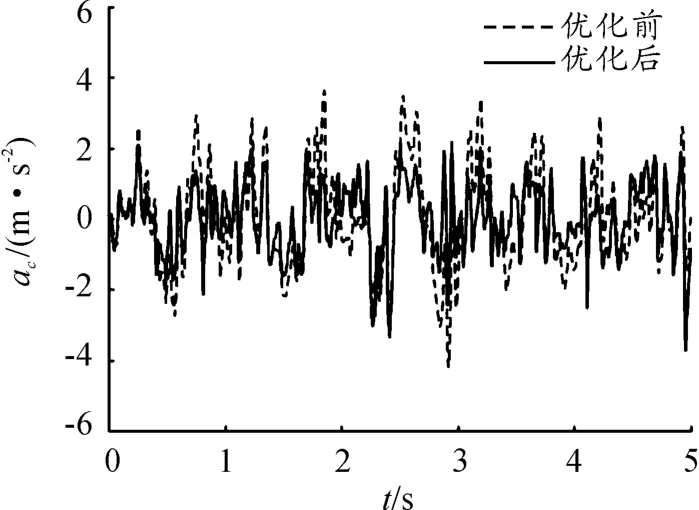
圖10 優化前后垂向振動加速度

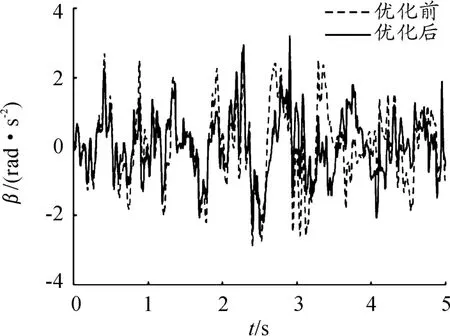
圖11 優化前后俯仰振動加速度

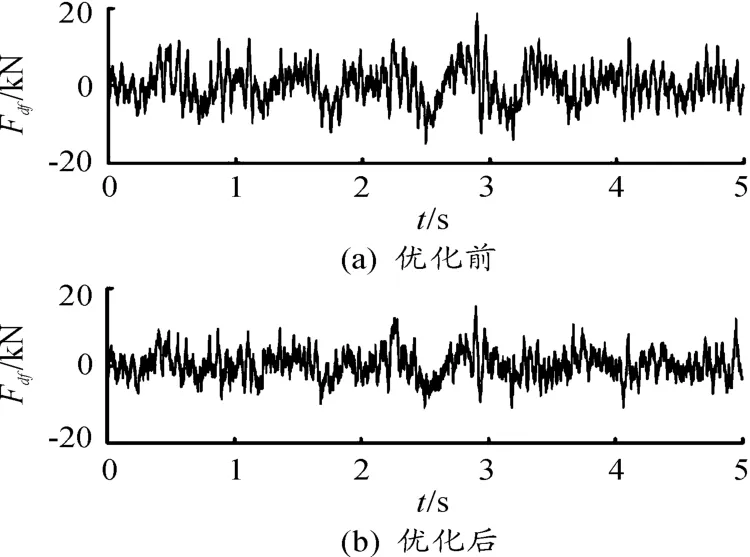
圖12 優化前后前輪載荷

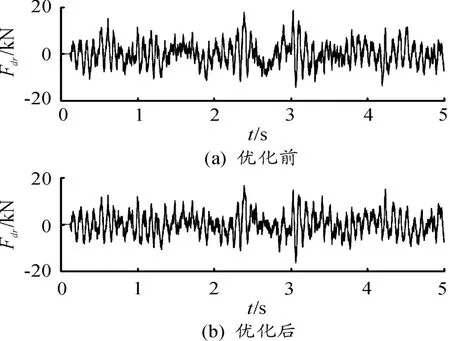
圖13 優化前后后輪載荷

4.3 優化效果驗證

優化時使用的路面條件為C級路面，車速為20 m／s。油氣懸架優化后，在不同的路面條件及車速下進行效果驗證，取平順性的重要評價指標，即垂向振動及俯仰振動的加權加速度均方根值來進行效果比較。驗證結果如表8所示。

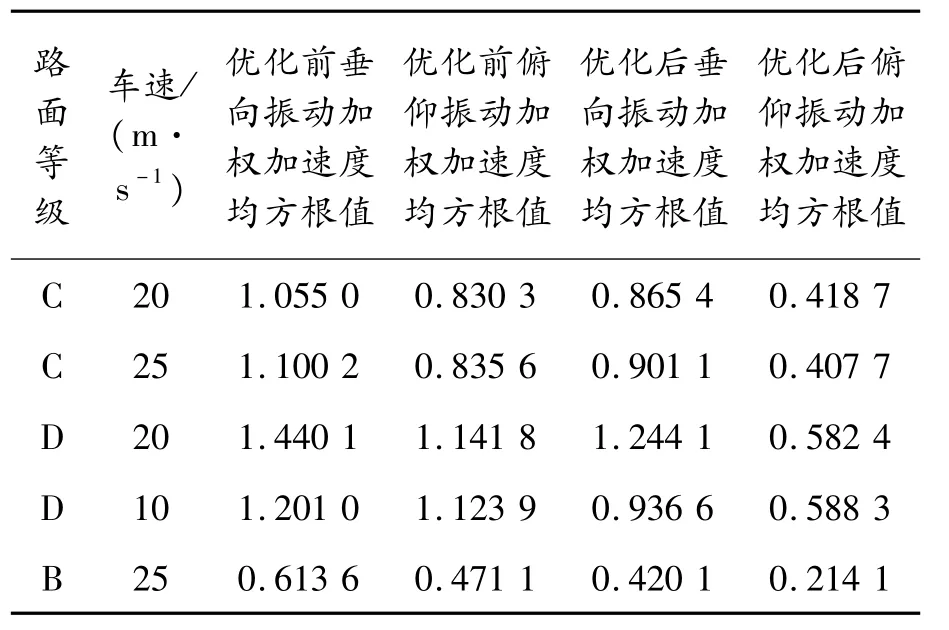
表8 優化前后不同環境下的平順性指標

由表8可知：不管在怎樣的路面條件及車速下，優化后的平順性都要優于優化前。優化后俯仰振動均有大幅度改善。除在D級路面25 m／s的車速下之外，其他條件下都將垂向振動加權加速度均方根值降至1以下，達到了使用優化前油氣懸架的子午線輪胎車輛的平順性水平，人的主觀感受為“有一點不舒適”（0.315～0.63）到“不舒適”（0.5～1）之間。由于忽略了座椅的減震性能，故實際給人的主觀感覺會更好，符合平順性的要求。而對于D級以上路面，則可通過適當降低車速來保證平順性。

5 結束語

機械彈性車輪的大徑向剛度特性會導致車輛平順性的降低。通過建立車輛平順性仿真模型，對在C級路面白噪聲輸入下以20 m／s車速行駛的裝配機械彈性車輪的越野車進行平順性優化，結果表明：各平順性評價指標皆得到了改善，優化后符合平順性要求。可見量子遺傳算法用于油氣懸架的多目標優化設計較好地完成了任務，具有一定的可行性。

本文僅考慮了半車的平順性，以后的工作可以綜合考慮整車、座椅及其他工況下的性能。本文采用的優化算法不失一般性，可以使用本文所闡述的方法同時通過改變各參數、優化目標、邊界條件等適用于不同行駛環境、車型以及設計目標，為油氣懸架的優化設計提供一種簡易可靠的方法。