上市券商股CAPM模型適用性及收益影響因素研究

王 堯，楊克磊

（天津大學管理與經濟學部，天津 300072）

對中國股市而言，2014年是不平凡的一年，上證綜指年漲幅逾50%，成為亞洲資本市場榜首，創全球金融危機以來最佳表現。以券商股板塊為例，年平均漲幅達160%，屢屢成為股民及媒體眼中的焦點，宏源證券、太平洋等漲幅更超過250%。在此大背景下，新股開戶數持續增加，天量資金涌入，如何選擇高收益的標的資產再次成為廣大股民迫在眉睫的問題。在各種新方法層出不窮、眾說紛紜的今天，我們不妨換個思維，重拾經典。

1964年，William Sharp［1］、John Lintner［2］和Jan Mossion［3］在 Harry Markowitz建立現代投資組合管理理論的基礎上，將其進一步發展為資本資產定價模型（CAPM）。作為現代金融理論的三大基石之一，資本資產定價模型給出了確定資產風險及其期望收益率之間關系的精確預測方法［4］。在猶如過山車般的中國股市，CAPM模型能否為投資人提供一種選擇標的資產的有效渠道，摒棄總風險，僅關注系統風險。如果CAPM模型在中國股市或其若干子板塊具有適用性，也就是說，影響單只股票收益率的最主要因素是其與整個市場共同變化的程度，那投資者在牛市選擇β系數高的股票，獲得高于大盤平均水平的超額收益，在熊市選擇β系數低的股票，在經濟蕭條的大背景下主動防御，使損失低于大盤平均水品，而β系數也是一個易于獲取且具有橫向可比性的指標；如果CAPM模型不具有預期中的適用性，那么影響某一類股票收益的因素都有哪些，該以何指標作為選擇投資標的參考，也是值得投資者關注的問題。

1 概述

關于CAPM模型在我國股市的適用性，眾多學者做了大量研究，但結果分為迥然不同的兩派：文獻［5］在深證A股中隨機選擇81只股票，通過時間序列檢驗和截面回歸2種方法，得出CAPM模型在深證股票市場并不完全適用的結論。夏裴［6］、黃振等［7］學者均認為 CAPM模型在中國證券市場不適用。文獻［8］隨機選擇了涵蓋各大行業的47只股票，通過分析得出結論：CAPM模型在上交所具有較好的適用性，且β系數的擬合優度高達0.997，系統風險對股票收益率的解釋能力很強。此外，文獻［9］分析了CAPM模型在鋼鐵子板塊中的適用性，得出鋼鐵行業β系數整體偏高的結論，在70%以上的鋼鐵股票中，系統風險對收益率有著較好的解釋能力。陸艷［10］、表二蘇等［11］也分別討論了CAPM模型在移動通訊行業、銀行業、電力行業、釀酒業等領域的適用性。

關于個股收益的影響因素，周孝華等［12］選擇了537支個股在5年內的月度收益數據，通過研究發現：收益率與市值正相關，與股票市凈率、凈營運資產等負相關。廈門大學的張菁［13］研究了我國上市銀行股收益的影響因素，發現銀行股收益與賬面市值比負相關，與市值呈現二次曲線關系。總的來說，券商股領域的CAPM模型適用性及收益影響因素研究都屬于較空白的領域，而隨著我國經濟政策的更加開放以及資本市場的日趨完善，券商股板塊的地位更加重要。本文的研究將在一定程度上彌補現有研究的不足，對券商股領域的行情分析及投資策略都有一定的現實和理論意義。

2 數據與方法

2.1 研究思路

本文擬選取我國A股上市的21支券商股，其中國信證券于2014年12月29日開始上市交易，故不在本文的研究范圍。研究時間為2012年1月1日—2014年12月31日，首先利用20支股票在這3年以來的收盤價，計算以周為單位的收益率，利用定義式求取20支股票的β系數并通過在時間序列上回歸的方法進行驗證，通過分析β系數研究我國券商股收益率對系統風險的敏感程度。再用157個時間點的橫截面數據，以β系數作為自變量，個股收益率作為因變量進行線性回歸，來驗證β系數與個股收益率的線性關系及其對收益率的解釋能力，從而得出CAPM模型對我國上市券商股是否適用的結論。若適用，則為投資者提供了一種簡單可靠的標的資產選擇方法；若不適用，進而討論上市券商股收益率的影響因素。

2.2 研究方法

CAPM模型適用性的實證研究一般采用歷史數據，構建模型（1）：

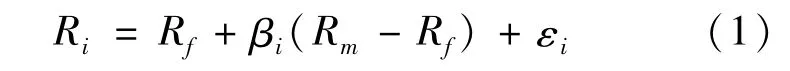
其中：Ri表示資產i的收益率；Rf表示無風險收益率；Rm表示市場收益率；βi表示資產i的β系數；εi為其他因素影響的度量。在同一時點下，Rm、Rf均為常數，若已知每個βi及其對應的Ri，便可進行回歸。

以往的研究中，β的計算均采用歷史數據回歸，而沒有采用定義式直接計算。為了提高數據的準確性，本文打算采用定義及回歸2種方法分別計算，再以兩者的平均值作為最終的β系數。得到β系數之后，就可作為模型檢驗中的自變量，采用橫截面數據，對同一時點一系列股票的β系數和收益率進行回歸，并進行檢驗，對模型（1）通過變形得到如下形式：

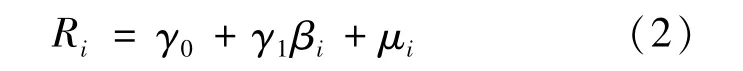
根據回歸結果就可得到結論。

2.3 樣本選取

本文樣本采用在我國A股上市的20家券商股，信息見表1。另從國泰安數據庫（CSMAR）獲得這20家上市券商從2012年1月1日—2014年12月31日每個交易日的收盤價作為基礎數據。

2.4 變量計算

2.4.1 收益率的時間間距

根據模型，首先需要確定時間間距t。計算β系數并驗證CAPM模型適用性的過程是對大量的歷史數據進行回歸的過程。就回歸分析的方法本身而言，樣本容量越大，回歸的效果越好。但是在較短的時間內，交易信息中可能包含偶發事件造成的噪音影響，為了既得到足夠的樣本量，又能剔除噪聲波動的影響，使數據真實可靠，必須將2個維度綜合考慮。本文選取的數據是2012年1月1日—2014年12月31日之間每個交易日的交易數據，時間間距t設為1周（一般為每周五的收盤價，如遇法定節假日則選擇距離周五最近的一個交易日的收盤價），于是得到157組收益率指標。

2.4.2 市場收益率

公式中的Rm是指市場收益率，通常用股票價格指數的平均收益率來代替。股票指數本質上是通過選取一組有代表性的股票來描述整個股票市場總的價格水平的變化，是整個股票市場的縮影，因此以股票指數的收益率替代理論上的市場收益率是可行的。我國股市中現有上證180指數、滬深300指數、央視50指數、上海證券綜合指數（簡稱上證綜指）、深證股票綜合指數等，它們分別從不同的方面反映股票市場的價格走勢。根據實際生活及研究中的習慣及指數本身的適用范圍，本文以上證綜指和深證成指為依據計算市場收益率：

指數收益率＝（當期收盤指數-上期收盤指數）／上期收盤指數

本文將上證綜指和深證成指的收益率取平均數，定義為綜合市場收益率Rm：

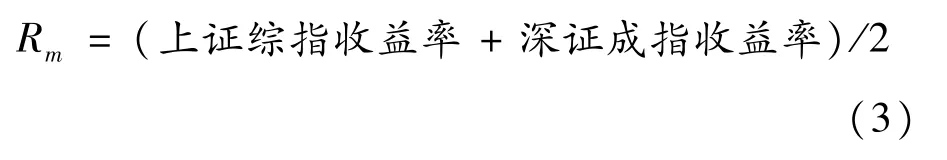
2.4.3 股票收益率

利用式（4）可計算時間間距t下的157組券商股周收益率。

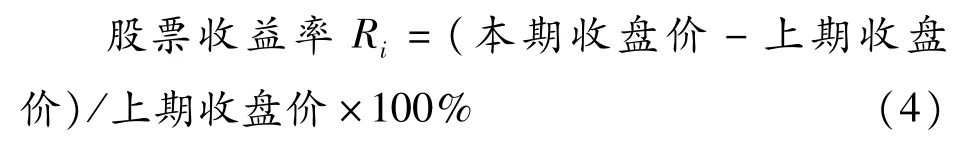
為了剔除股票除權除息對價格的影響，本文采用的收盤價均為復權價格。此外，在研究期內，5家股票因重大事項停牌，造成一部分期間內交易數據的缺失，且西部證券于2012年5月3日上市交易，在此之前也沒有交易信息。為了減少缺失的交易數據對分析結果的影響，在根據定義計算β系數以及回歸過程中，本文對缺失的部分直接從樣本中予以剔除，剔除數據最多的宏源證券剩余117組數據，仍屬于大樣本，認為數量減少對計算結果不會造成實質性差異。

2.4.4 無風險收益率

無風險利率是指將資金投資于某一項沒有任何風險的投資對象而能得到的利息率，這是一種理想的投資收益。在金融資產的定價研究中，無風險利率一般指投資者可以在此利率下進行自由借貸。國外的實證研究中多以短期國債利率或銀行同業拆借利率來代替。在文獻［14］中，指出了我國債券交易市場不統一、期限結構不合理，以及銀行同業拆借利率隱含了銀行自身經營風險等缺點，因此無法利用成熟資本市場中的方法選擇無風險利率。考慮到我國居民仍以儲蓄作為最主要的投資方式、大型商業銀行違約率極低以及央行指導利率的高適用性，本文擬用銀行存款利率代替無風險利率，且我國股市多以短線持有賺取資本利得為主，故選擇3個月定期存款利率，定義為Rf。

2.4.5 β系數

如本文所述，β系數的定義式為

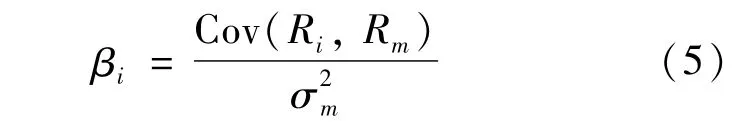
已知Rm和Ri（其中i為1～20支券商股股票），利用excel自帶的covar和varp函數公式可求得20支券商股的β系數。對模型（1）適當變形得到如下模型：

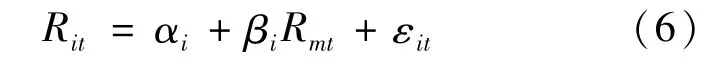
這個回歸方程通常被稱為“一次回歸”方程，在每一個時點 t下，Rmt＝Rm-Rf，而 Rit＝Ri-Rf，對每一支股票的收益率Rit與均衡市場組合的收益率Rmt進行時間序列的回歸，也可得到一組β系數，將2組數據求平均數，從而得到最終的 β系數。

3 實證分析與檢驗

3.1 β系數的實證分析與檢驗

要利用歷史數據回歸求得β值，首先要求模型（6）中的Rit和Rmt線性關系成立，并進行異方差與序列自相關的檢驗。

用SPSS18處理數據并得到如圖1所示結果。

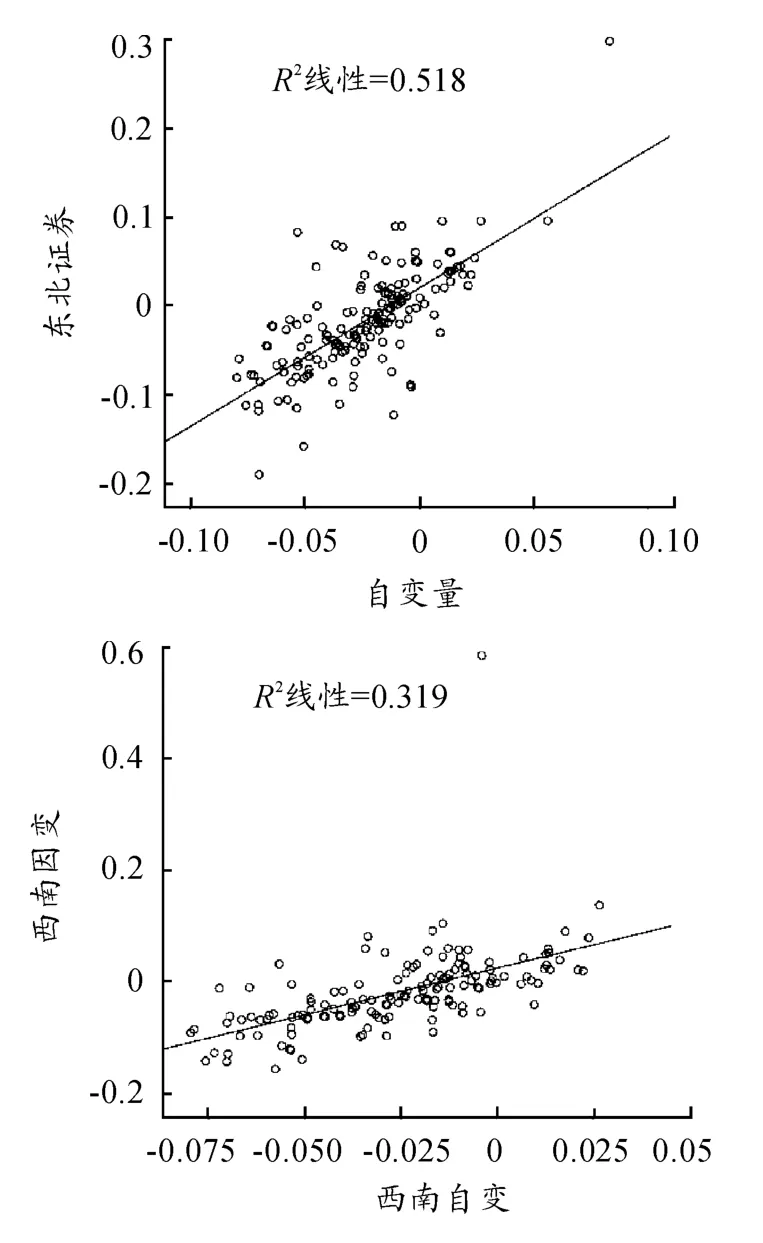
圖1 異方差檢驗的散點圖

用圖示法進行異方差的檢驗（如圖1所示），分別做出20支股票自變量和因變量的散點圖，如果模型（1）中的隨機項εi存在異方差，則隨著自變量的增大，因變量偏離回歸直線的離散程度將增大，使得點集呈現出三角形狀或啞鈴形狀。觀察圖像發現，散點與擬回歸直線之間沒有明顯的遞增或遞減的偏離趨勢，則說明模型中的隨機項是同方差的。

進行序列自相關檢驗，給定顯著性水平α＝0.05，查Durbin-Watson分布表，當樣本容量為T＝157時，得到臨界值 dL＝1.72，dU＝1.747。

當0＜d＜dL時，說明隨機項存在一階自相關；當4-dL＜d＜4時，說明隨機項存在一階負自相關；當dU＜d＜4-dU時，說明隨機項不存在一階自相關；當dL＜d＜dU或4-dU＜d＜4-dL時，則不能判別隨機項是否存在1階自相關。

再觀察可見，R2的平均值為0.51，T值的平均值為12.77，最小值為5.8，說明線性關系顯著且自變量對因變量有很高的解釋能力，說明回歸效果較好，結果可信。用回歸方法得到的β值和定義式求得的β值平均后得到20只股票最終的β系數，見表2。

3.2 CAPM模型適用性的實證分析與檢驗

得到每一支券商股的β系數之后，就可以在157個時間點分別用β系數和與之對應的收益率進行橫截面上的回歸，結果描述如表3所示。

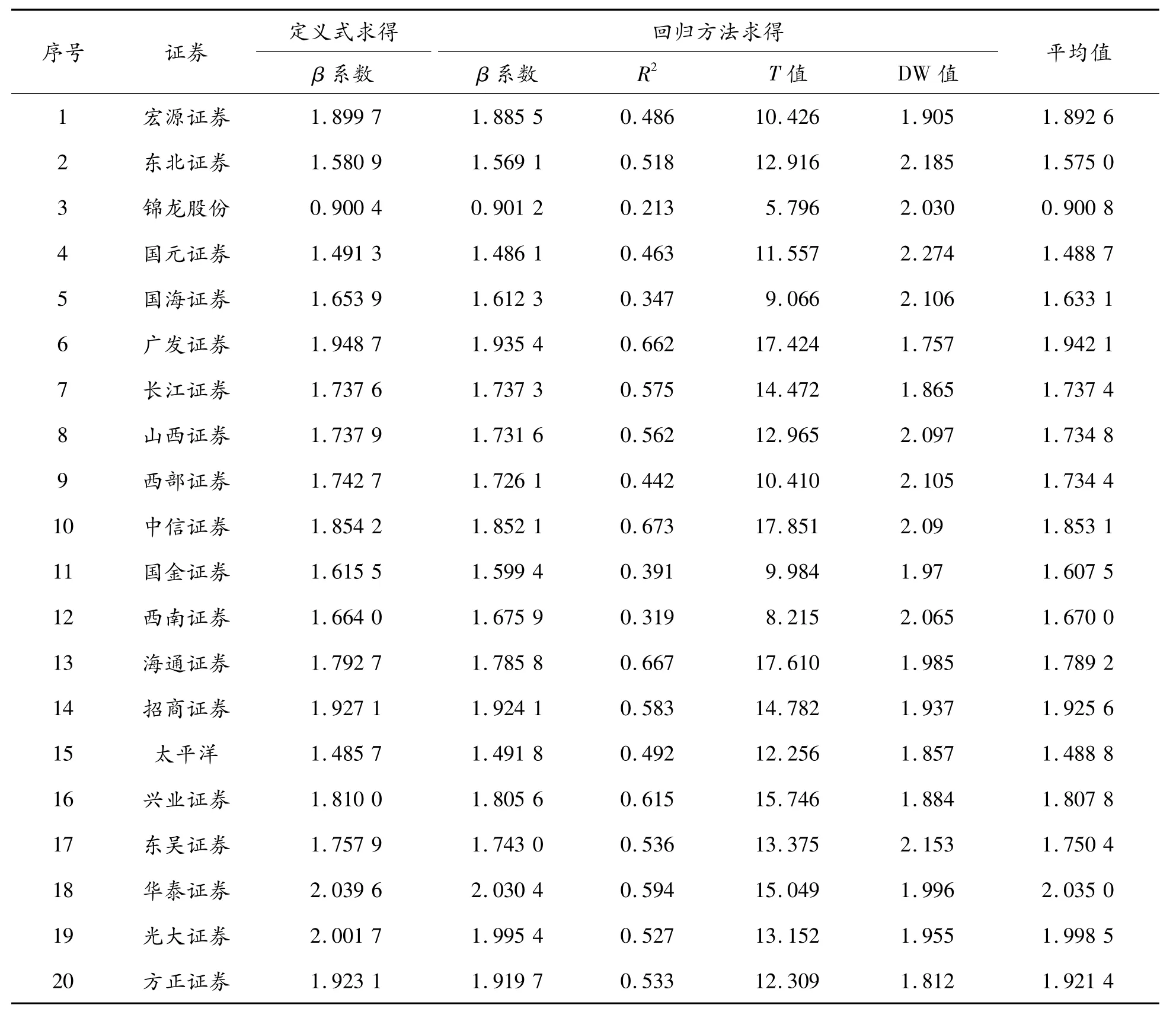
表2 β系數的計算結果

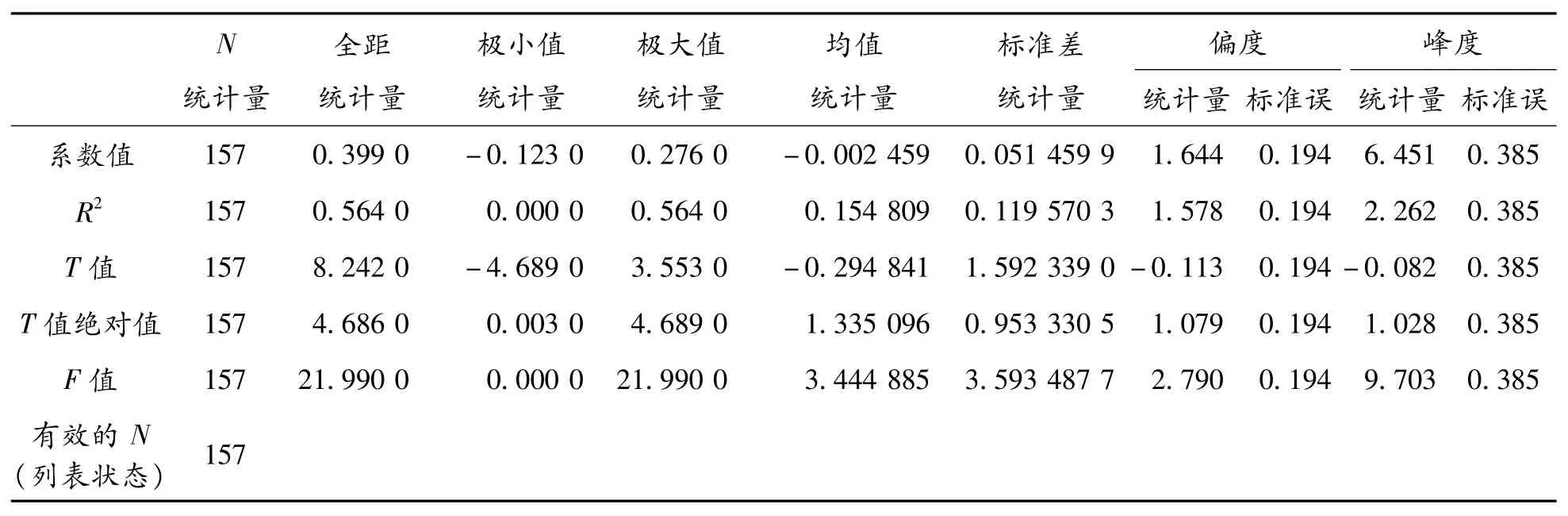
表3 CAPM模型回歸結果的描述統計量

R2的平均值為0.155，擬合優度不理想，說明β值對個股收益的解釋能力平均只有15.5%。進行回歸參數估計值的顯著性t檢驗，T絕對值的平均值為1.335，勉強通過顯著性水平α＝0.10時的檢驗。即當α＜10%時，β系數對股票收益率沒有顯著的線性關系；當α≥10%時，線性關系成立。在157組數據中，T值絕對值大于臨界值的有87組，占比55.41%。在模型的整體顯著性檢驗中，F的平均值為3.44，而α＝0.1時，自由度為（1，18）的F分布的臨界值為3.01，則模型整體在α＝10%的水平下顯著。

3.3 券商股收益率影響因素的實證分析

通過上一步的分析，發現β系數雖然與股票收益率線性相關，但對其解釋能力僅有15%，因此仍然有其他因素能夠影響個股收益。根據Fama-French的三因子模型，認為上市公司的市值、賬面市值比、市盈率可以解釋股票收益率的差異，因此定義并引入如下變量。

市值（SZ）等于每一個時點下，股票市場價格乘以股份數的積，因為我國股權分置改革的最終目的是實現股份的大流通，因此此處的股份數是指企業賬面中的股本（實收資本），包括流通股和非流通股；賬面市值比（ZM）是指該時點下所有者權益總額與市值的比，此處的賬面權益應包括實收資本、資本公積、未分配利潤以及少數股東權益等；市盈率（PE）等于當前市價除以每股收益。

每一個時點的收益率為本時點的收盤價較上一時點收盤價的漲（跌）幅（例如2014年中期收益率是2014年6月30日股票收盤價較2013年12月31日股票收盤價的漲幅），根據20家券商的財務數據，計算上述變量的值并分別與股票收益率進行回歸，結果如表4所示。

在顯著性水平α＝0.05，T＝20，k＝1的情況下，隨機項不存在1階自相關的DW值范圍為（1.41，2.59），則所有回歸方程均不存在序列自相關。市值與收益率回歸結果的R2為0.05，擬合度非常低，T值絕對值為0.882 2，F值為1.049 8，模型整體及參數估計值均不顯著；賬面市值比、市盈率與收益率的回歸結果均不能通過F檢驗及T檢驗。考慮現實情況中，投資者獲得財務報表信息后會影響其投資意愿，而投資意愿的改變造成股票價格的變動，最終影響到下一期的收益率，也就是說本期的財務信息并不能立刻被投資者吸收并反映在本期的收益率上，而是會影響下一期的收益率，按照此種思路將收益率滯后一期再與市值、賬面市值比和市盈率等自變量回歸。

新的回歸結果中，市值作為自變量的回歸仍然不能通過F檢驗和T檢驗；在α＝0.1的顯著性水平下，T（18）的臨界值為 1.33，F（1，18）的臨界值為3.01，則賬面市值比、市盈率與收益率的線性關系顯著，且對收益率的解釋能力分別為15%和19%，均是影響股票收益率的重要因素之一。

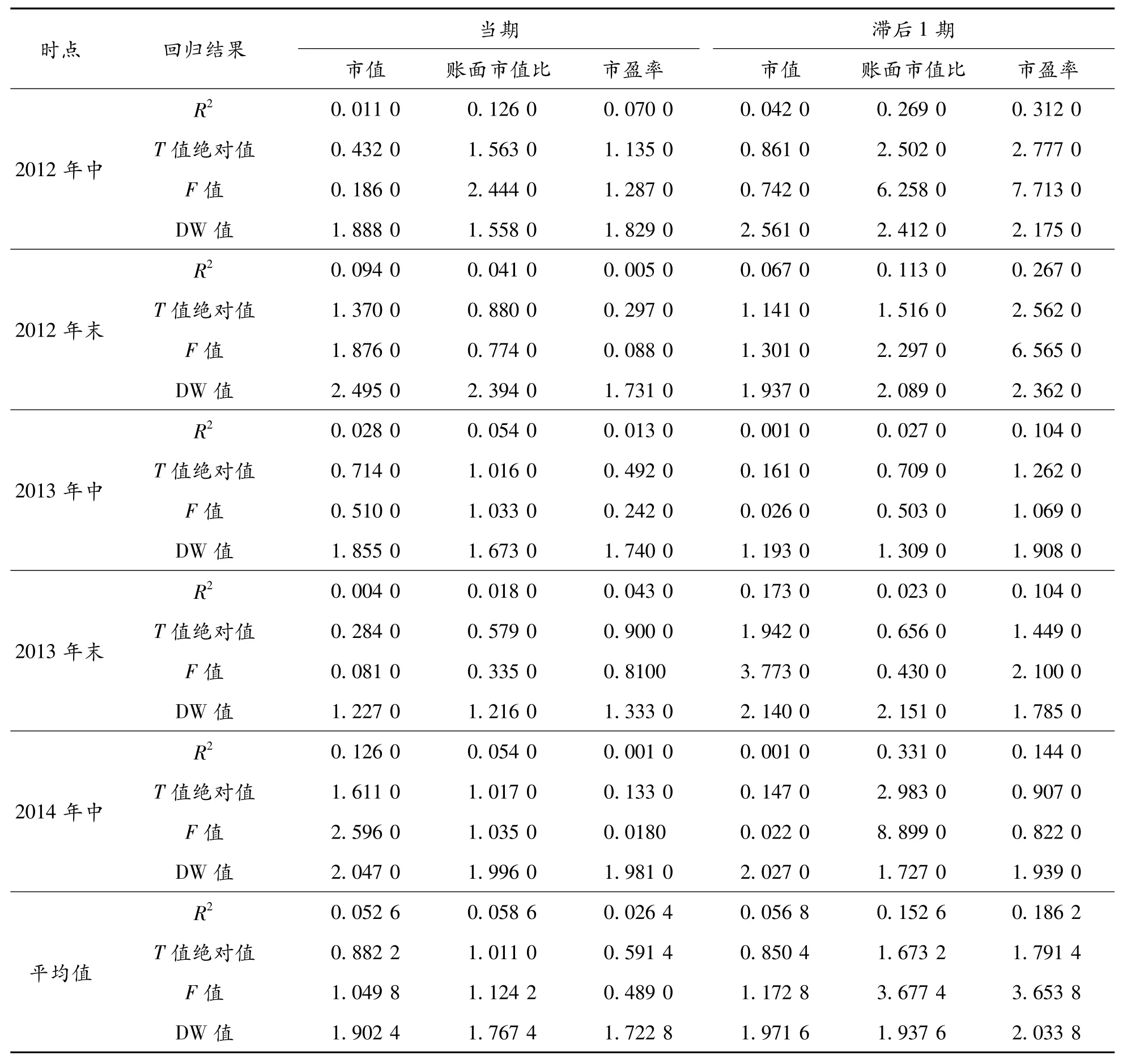
表4 收益率影響因素的回歸結果

4 結束語

根據本文實證分析，發現券商板塊股票的β系數整體偏高，平均值為1.724 3，最大值為華泰證券2.035，僅有的β系數小于1的錦龍股份為0.901，而其低于1的主要原因可能是雖然錦龍股份在股票分類中屬于證券板塊，但其僅僅是控股中山證券、參股東莞證券，其主營業務一半是自來水業務，并非真正意義上的券商股。券商股β系數整體偏高說明其波動程度遠高于大盤平均水平，風險高、投機性強、對信息的反應敏感且劇烈。而券商股在股市的實際表現也確實如此，無論是在滬港通、央行降準等利好消息下的帶頭瘋長，還是在原油走熊、資本監管等利空消息下的集體跳水，尤其是在2015年初的119暴跌中，券商股板塊集體跌停，充分體現了券商板塊是整個股市的“風向標”，作為牛市的帶頭大哥，現階段值得投資者關注。

從本文3.2節的實證分析來看，CAPM模型在我國現階段的券商股板塊適用性并不很高，系統風險對收益率變動的解釋能力不足20%，雖然通過了參數估計值的顯著性T檢驗，說明β系數確實影響收益率，但絕非主要因素，投資者在選擇標的資產時，可參考其β系數，但不應該將其作為主要的選擇標準。

通過本文3.3節的實證分析可見：Fama-French的三因子模型并不完全適用我國現階段的券商股板塊，市值對收益率并沒有顯著的影響，而賬面市值比和市盈率對滯后一期的收益率有一定的影響，但解釋能力均小于20%。

綜上所述，CAPM和三因子兩大經典模型適用性欠佳，再次說明我國資本市場發展尚不成熟，投資者機構畸形，以個人為主體；投資觀念不成熟，以盲目投機為主，羊群效應顯著；信息披露不充分，大小投資者之間存在信息不對稱；股權結構不合理，行政干預過多。在這樣一個不成熟的市場，投資者切忌根據簡單的模型和單個指標選取標的資產，應該綜合考慮賬面市值比、市盈率等多個指標，并密切關注經濟大環境下股票市場整體的牛熊行情，充分利用 β系數增加收益、規避損失。