彈丸擠進過程中彈帶變形仿真分析

梁興旺，李 強，安俊斌，程宇陽

(1.中北大學 機電工程學院， 太原 030051; 2.中國人民解放軍75130部隊， 廣西 貴港 537100)

擠進過程作為身管武器發射過程的起始過程，在整個內彈道過程中占有相當重要的地位。對彈丸的發射過程來說，彈帶沿膛線運動并形成刻痕為彈丸的旋轉提供導向作用，并且彈丸在擠進過程中彈帶的塑性變形為彈丸的沿膛運動密閉火藥氣體[1]。

由于彈丸擠進過程涉及高沖擊、高壓、高溫，大變形等過程[2]，因此對彈丸擠進進行試驗研究是非常困難的。通常對彈帶變形的實驗研究主要是通過回收發射后的彈丸，例如殷軍輝等[3]通過研究發射后的彈帶硬度分布及組織演變規律，得到發射后的彈帶宏觀形變的細觀與微觀規律。現階段大多數對彈帶擠進過程的研究均通過有限元方法進行，王鵬等[4]采用非線性有限元方法對某大口徑火炮彈帶擠進過程的力學機理進行研究，得到彈丸擠進運動規律、動態擠進阻力及擠進壓力值，獲得了摩擦性質對彈帶擠進過程的影響規律；孫全兆等[5]通過數值模擬研究彈帶的動態擠進過程，分析彈帶變形及刻槽形成過程；孫河洋等[6]以彈塑性有限元接觸理論研究彈帶擠進過程，分析了兩種不同結構坡膛條件下的彈帶擠進過程。

小口徑火炮由于彈丸長度較短，后定心部即為彈帶。彈帶一般為圓柱形。為便于彈帶嵌入膛線并且減少彈前空氣阻力，其前后端面均設置為斜面，前方與火炮坡膛錐角對應，后方用來存放擠進過程中發生塑性流動的彈帶。本文以某小口徑火炮為研究對象，通過對擠進過程中的彈帶受力進行理論分析以及彈丸擠進膛線過程的有限元仿真，研究彈帶在擠進過程中的變形規律。

1 擠進過程中的彈丸受力分析

1.1 擠進過程中的彈帶受力情況

彈丸在擠進坡膛的過程中，彈帶與坡膛之間產生擠壓變形，坡膛對彈帶產生一定的擠壓應力，彈帶的受力模型如圖1所示，其中α為坡膛角、β為膛線纏角；Fg為身管陰線擠壓彈帶的力、Fl為身管陽線擠壓彈帶的力、Fc為身管坡膛擠壓彈帶的力、Fd為身管導轉側擠壓彈帶的力、Fu為身管非導轉側擠壓彈帶的力。

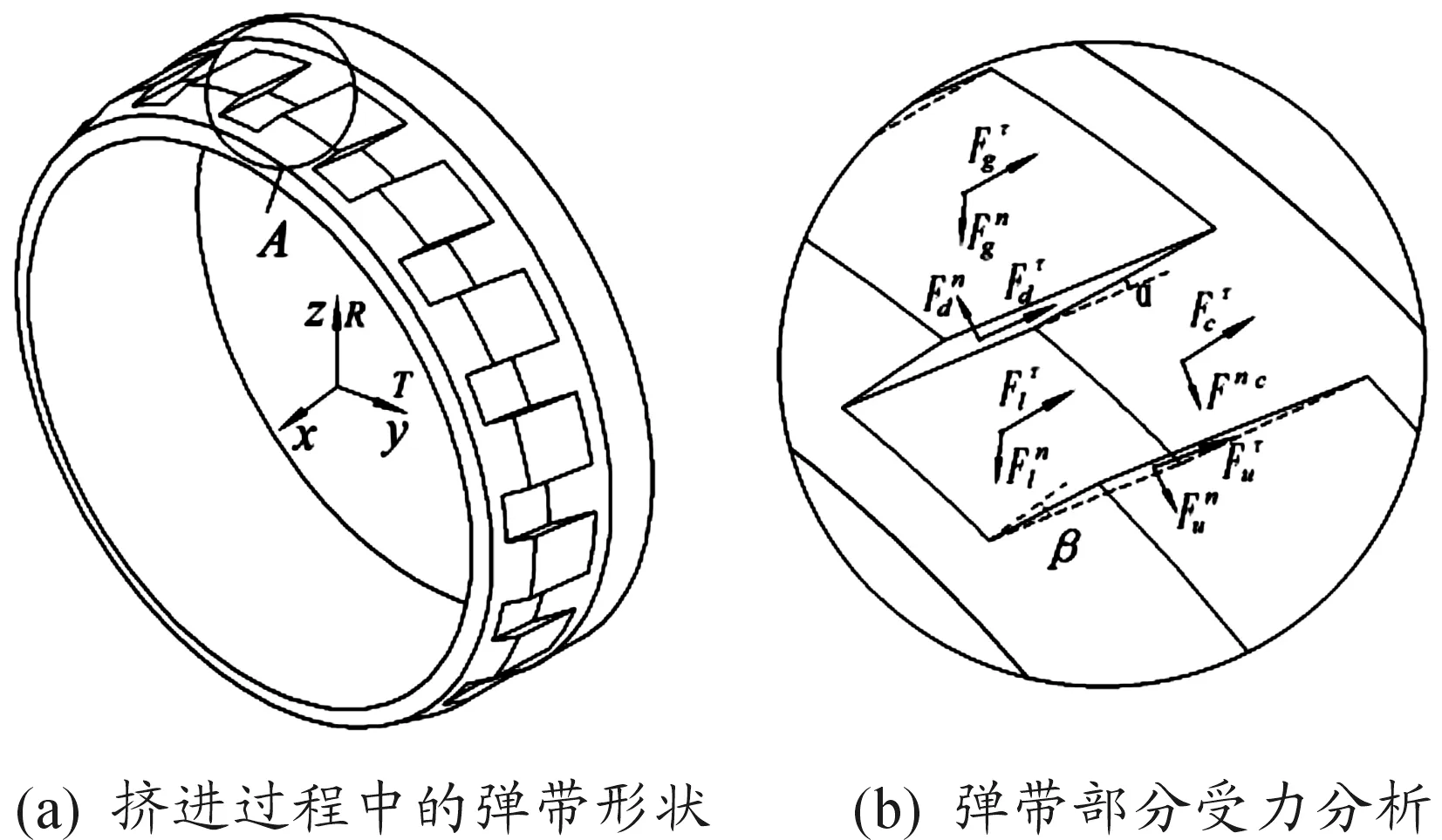
圖1 擠進過程中的彈帶受力示意圖

對彈丸所受的力進行分析，可得彈丸受到的被動力為

F=Fg+Fl+Fc+Fd+Fu

(1)

設各個接觸面的面積為Sg、Sl、Sc、Sd、Su，則上述彈帶所受到的力可由他們表面所受的法向應力σ、切向應力τ來表示，法向應力、切向應力之間與摩擦因素f成正比

τ=fσ

(2)

(3)

彈帶在身管軸線方向所受到的力為

Fx=Fgx+Flx+Fcx+Fdx+Fux

(4)

式中，

(5)

其中n為膛線條數。

彈帶在身管周向方向所受到的力為

FT=FgT+FlT+FcT+FdT+FuT

(6)

式中，

(7)

1.2 擠進過程中的彈底壓力[7]

彈丸在擠進過程中受到的主動力為火藥燃氣給予彈丸的彈底壓力，而由經典內彈道學計算出的膛內壓力是膛內平均壓力，彈底壓力可由平均壓力計算得出

(8)

式中：pd為彈底燃氣壓力，p為膛內平均壓力，ω為裝藥質量，φ1為僅考慮彈丸旋轉和摩擦的次要功系數，m為彈丸質量。

在已知發射藥的火藥特性參數后，可以通過經典內彈道學中的方法計算出膛內的平均壓力，再通過式(8)計算出彈底壓力。

2 彈丸擠進過程的有限元模型

以某小口徑火炮為研究對象，建立其身管與彈丸的三維模型，考慮到彈丸裝填時與身管坡膛之間存在一定的間隙，按照彈丸與身管的實際相對位置進行裝配，如圖2所示。彈丸擠進坡膛長度為10 mm，為了節約計算時間，取身管自坡膛位置起25 mm處。

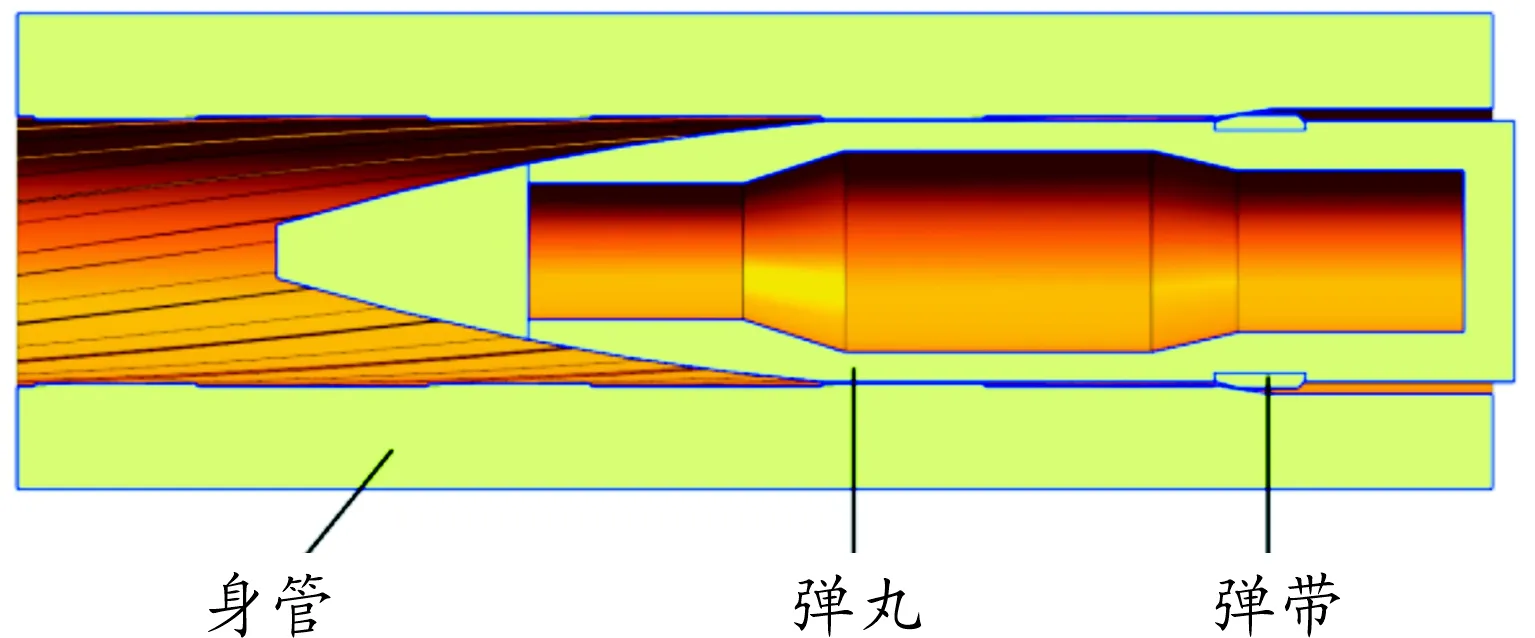
圖2 身管及彈丸三維模型

對建立好的身管與彈帶的三維模型進行有限元網格劃分，如圖3所示。利用Hyper Mesh有限元前處理軟件對身管、彈丸、彈帶劃分C3D8R網格，選用彈帶為0.2 mm，身管為0.1 mm的網格尺寸方案，其中彈帶網格數量為218 500，身管網格數量為3 619 680，彈丸網格數量為970 704。

圖3 身管與彈帶的有限元模型網格

由于在彈丸擠進過程中涉及材料的塑性流動、大變形、高應變率等非線性過程，因此彈帶的材料模型采用Johnson-Cook本構模型。此外，由于在彈丸擠進過程中涉及到材料的失效及損壞，因此在材料模型中引入Johnson-Cook失效模型[8-9]。彈帶材料采用紫銅，其Johnson-Cook參數如表1所示。

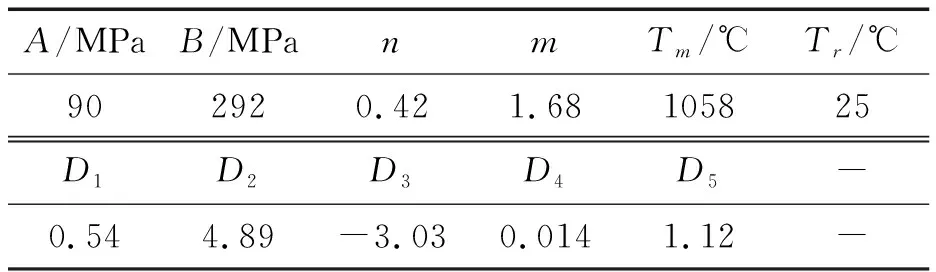
表1 紫銅的Johnson-Cook參數

由前述分析可知，彈丸擠進坡膛過程中受到的主動力為彈底燃氣壓力[10]，因此對彈丸尾部橫截面處施加壓力載荷；身管的固定方式為炮尾連接槽固定，因此在仿真過程中，將身管尾部施加固定約束，固定其六個方向的自由度；考慮到擠進過程是兩個相互接觸面相互作用的結果，設置接觸類型為通用接觸，切向行為選用摩擦因素為0.05，法向行為選用“硬”接觸。擠進過程的載荷與邊界條件施加模型如圖4所示。

圖4 擠進過程的載荷與邊界條件施加模型

3 彈帶變形仿真分析

運用ABAQUS有限元軟件對彈帶擠進模型進行仿真分析，設置求解模式為幾何非線性，并采用動力顯式(Dynamic，Explicit)求解器對上述模型進行求解。求解完成后，對彈帶的變形過程進行分析。

1) 擠進過程中彈帶變形過程

圖5為擠進過程中不同時刻彈帶變形圖。從圖中可以看出，彈帶與身管開始接觸時，彈帶前部逐漸擠入膛線，彈帶表面刻痕逐漸形成。彈丸繼續向前運動，彈帶上由膛線導致的刻痕不斷加深，并向后延伸。彈帶材料發生塑性流動，彈帶后部長度略有增加，彈丸逐漸加速，彈帶后部經過坡膛結束位置后，整個擠進過程結束。總的來說，彈帶刻痕的形成過程有著由淺至深、由窄到寬的特征。

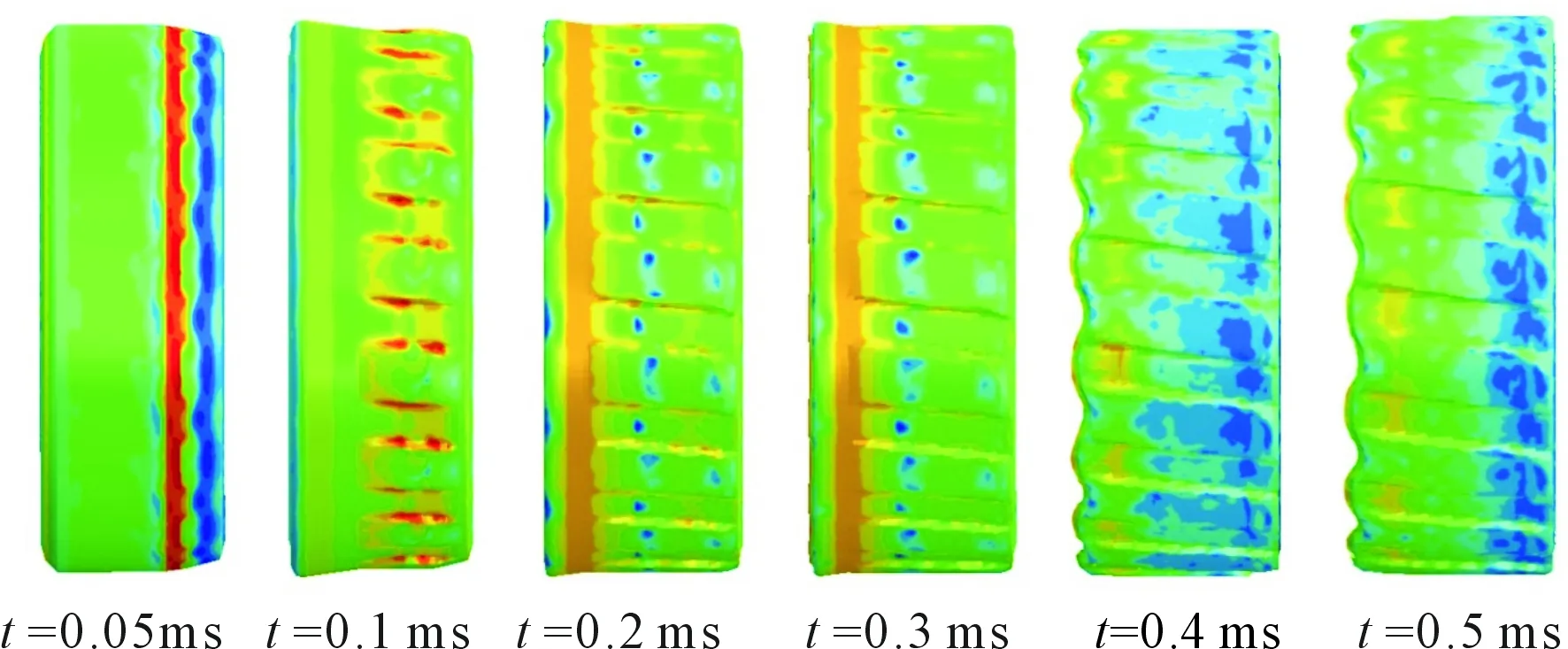
圖5 不同時刻彈帶變形圖

2) 彈帶刻痕上應力分布規律

為研究彈帶在刻痕位置處的應力分布規律，在彈帶前部、彈帶后部分別選取兩條路徑，路徑起點為路徑右端，終點為路徑左端，如圖6所示。分別在0.05 ms、0.1 ms、0.2 ms和0.3 ms時刻繪制兩條路徑上Mises等效應力曲線如圖7所示，研究彈帶刻痕軸向周向上應力變化規律。

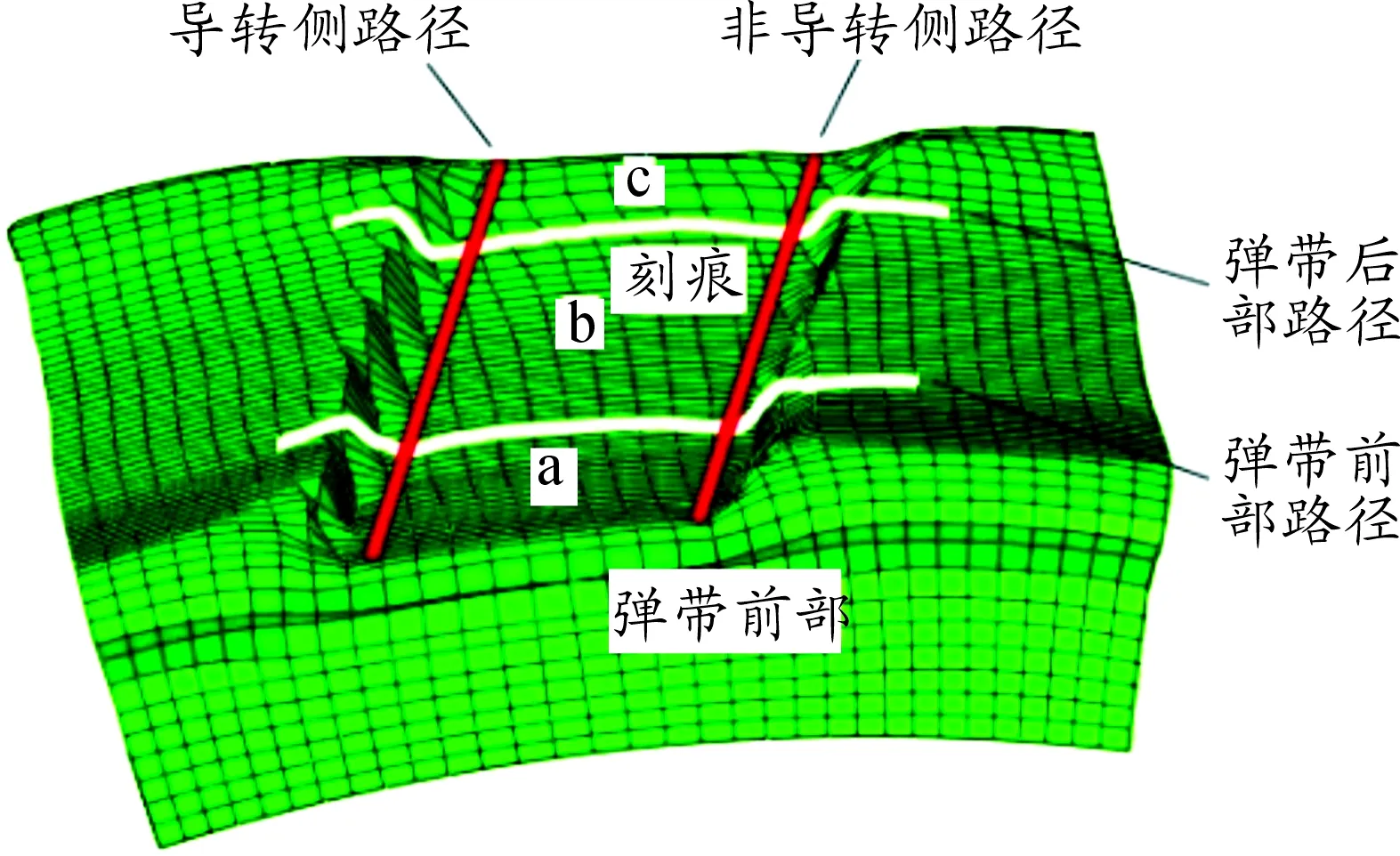
圖6 彈帶路徑示意圖

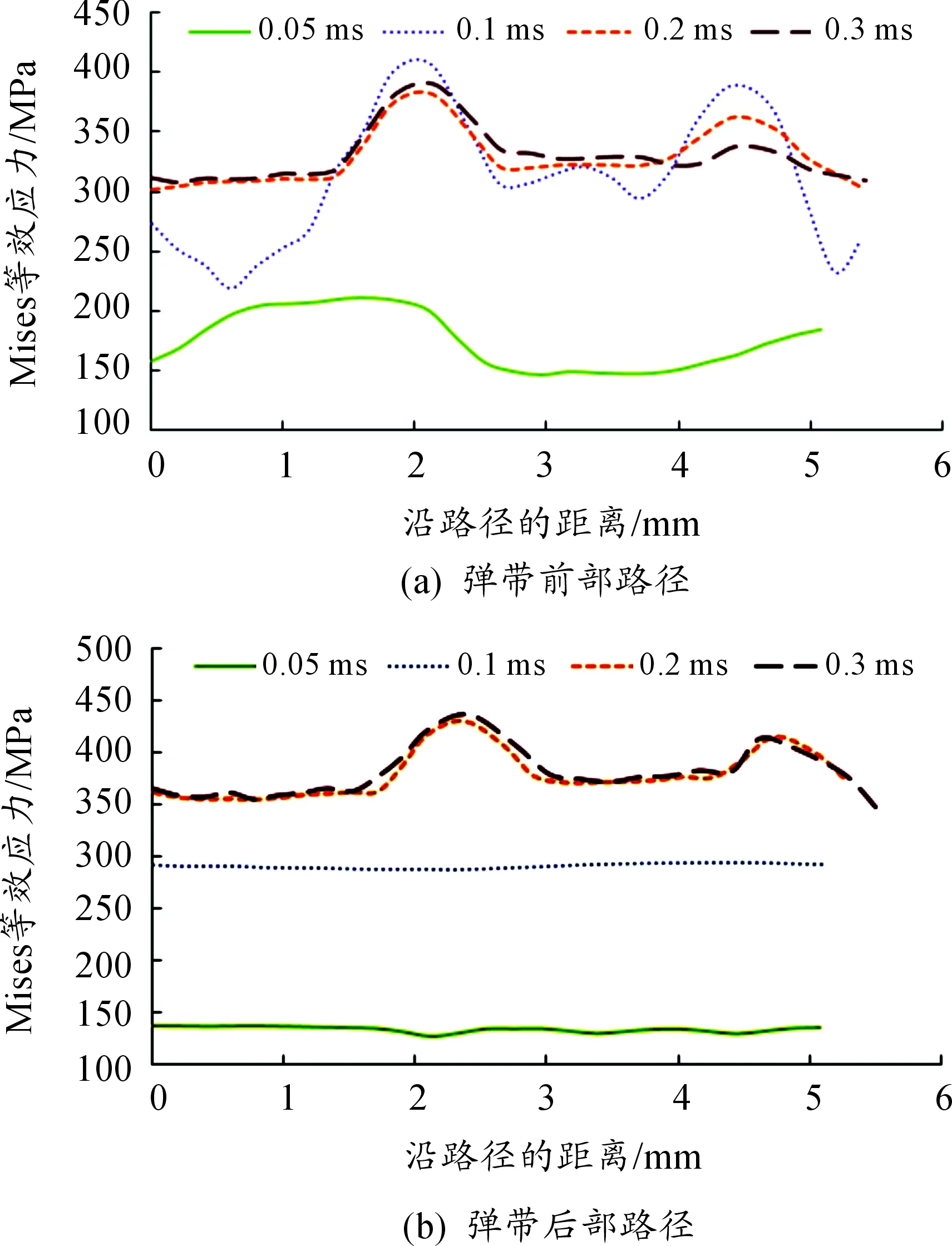
圖7 不同時刻彈帶路徑應力曲線

由圖7分析得出，擠進結束后，彈帶前部非刻痕處應力為310 MPa左右，刻痕底部應力為330 MPa左右，刻痕導轉側與非導轉側部位應力為350～400 MPa；彈帶后部非刻痕應力約為360 MPa，刻痕中部應力約為370 MPa，刻痕導轉側與非導轉側部位應力為410～430 MPa。總體來說，彈帶后部應力大于彈帶前部應力，這是由于隨著擠進過程的進行，彈帶前部的材料發生塑性變形，被擠至后部，導致彈帶后部內應力增加。此外，沿彈帶周向路徑，刻痕部位的導轉側和非導轉側應力比刻痕底部應力大，其中非導轉側應力略大于導轉側應力。這是由于彈丸在擠進坡膛的過程中，由于膛線的存在而使得彈帶擠入膛線時與坡膛導轉側與非導轉側之間相互擠壓所致，由于導轉側對彈丸導向的作用，使得彈帶上導轉側材料向非導轉側流動，使非導轉側的應力加大。

3) 彈帶刻痕形成過程

為研究彈帶刻痕由淺至深、由窄到寬的形成過程，選取彈帶刻痕導轉側和非導轉側上兩條路徑，路徑起點在彈帶前部，終點在彈帶后部，如圖6所示。繪制不同時刻下刻痕深度沿路徑的曲線，如圖8所示。

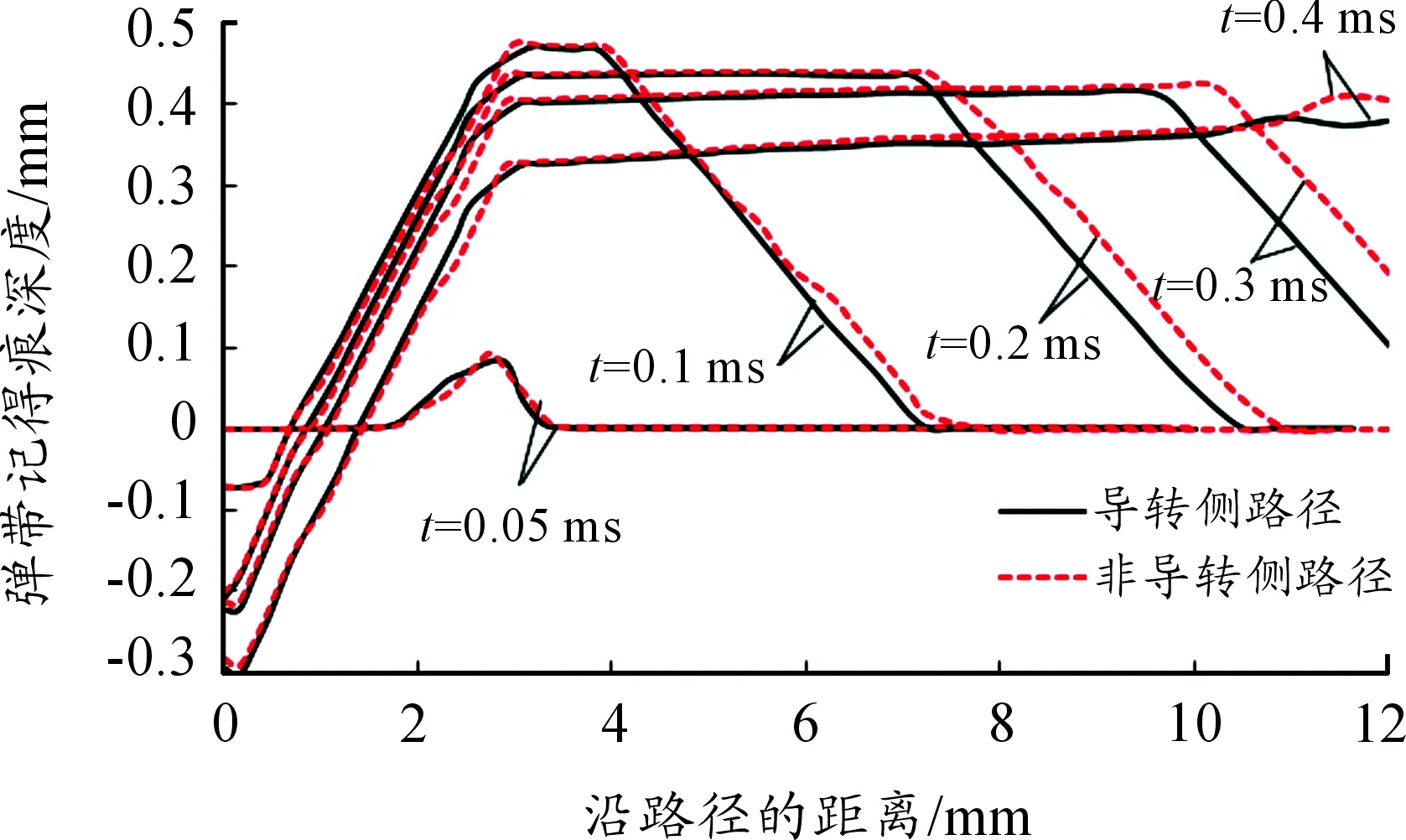
圖8 不同時刻下彈帶刻痕深度

從圖8中可以看出，不同時刻下導轉側路徑和非導轉側路徑上的刻痕深度變化規律是非常接近的。彈帶前部的刻痕深度由深到淺、由窄到寬逐漸成形，彈帶材料在與身管接觸部位向前向后均有流動，致使刻痕深度由最初為零達到最大值0.471 mm后又逐漸降低至擠進結束時降到0.332 mm。對比彈帶前部和彈帶后部刻痕，前部刻痕深度至擠進結束時比后部淺0.04 mm，即刻痕成形后其刻痕深度由前至后略有增加。

從彈帶上由前至后依次選擇a、b、c三處對其刻痕寬度進行測量，a、b、c位置的選取如圖6所示。得到不同時刻下的刻痕寬度數據，見表2。

隨著時間的推移，三處刻痕寬度均在不斷增加，擠進結束時a處刻痕達到2.495 mm，b處為2.463 mm，c處為2.264 mm。同一時刻下a處寬度最大，c處最小。彈帶刻痕寬度為前部稍寬，后部較窄。

4 結論

1) 在某小口徑火炮發射炮彈時，彈帶在擠進過程中的彈帶刻痕形成規律為前部深度隨時間由零到深再到淺，由前部至后部逐漸加深，其寬度隨時間逐漸加寬，由前至后寬度逐漸減小。

2) 本文可為相關設計人員對彈帶與身管坡膛的設計提供參考。

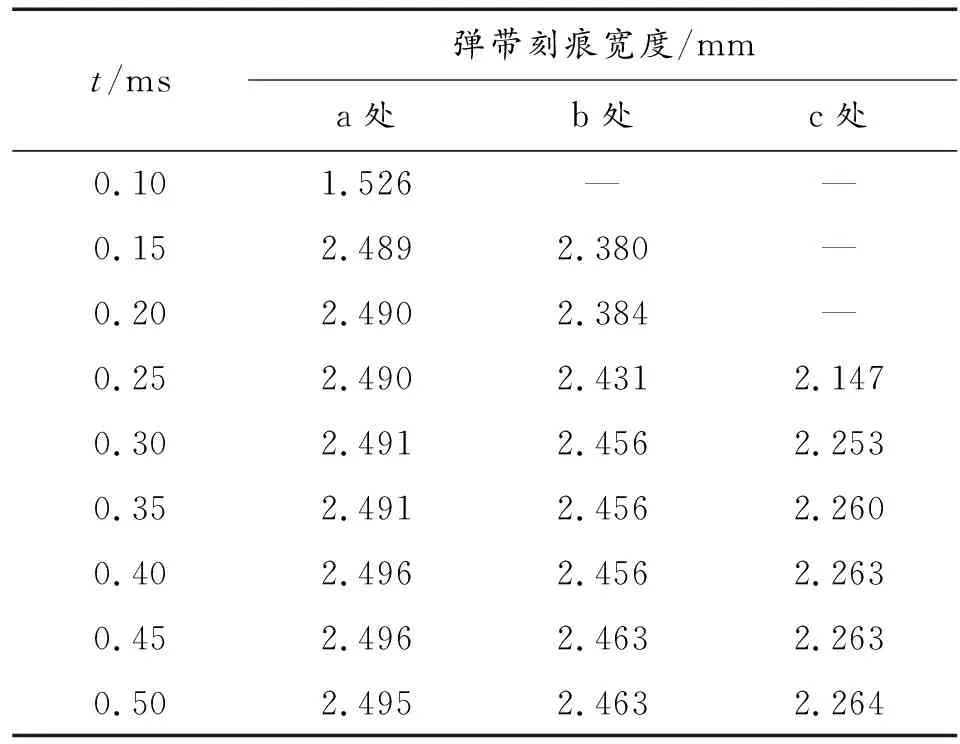
表2 不同時刻彈帶刻痕寬度