磨床冷卻系統的可靠性建模及評估研究??

劉 超 白 強 馬慶鋒 楊振林 戰智濤

(齊魯工業大學(山東省科學院)山東省科學院海洋儀器儀表研究所，山東青島266061)

隨著現代制造業的高速發展，對數控磨床的要求也越來越高。數控磨床作為集機、電、液、光于一體的現代化制造裝備，主要應用于航空、航天、汽車等高精密工件的加工上，由于本身集成的復雜性，就會對其可靠性提出較高的要求。對比國外進口的數控磨床，國產的數控磨床在可靠性方面還存在很大的差距。因此，加快數控磨床可靠性提升工程已尤為重要。國內外學者對數控機床可靠性方面做了大量的研究工作。俄羅斯的研究人員對產品的可靠性提升的具體措施作了研究[1]。Kerr等人用計算機圖像處理技術對機床的刀具磨損進行了在線監測，評估了刀具剩余壽命[2]。日本新潟大學的藤井義對加工中心進行現場跟蹤試驗，并對加工中心進行故障分析，對其可靠性指標進行了評估[3]。申桂香等通過賦權的方法對數控機床的可靠性進行評價[4]，廖雯竹等針對設備可靠性隨使用年限以及維修次數的增加而降低情況，建立了基于設備可靠性的順序預防性維護優化模型，引入威布爾分布對某列車檢修設備進行仿真分析[5]。大部分都是對整機進行可靠性評估，對數控磨床子系統進行研究的比較少，所以對數控磨床子系統進行可靠性評估顯得尤為重要。

1 故障數據預處理及散點圖的繪制

對于故障數據的采集和預處理有多種方式[6-7]。繪制故障時間分布函數以及概率密度函數的散點圖，可以使用等時間頻次法以及經驗分布函數法。使用兩種方法對故障時間進行處理，可以較好地減小誤差，在進行綜合分析后進行數據擬合，可以減小擬合的范圍，減小工作量。

1.1 等時間頻次法

使用等時間頻次法是為確定時間區間的大小，時間區間的大小決定出現故障時間頻次的多少，進而影響區間內散點的多少，使得獲得概率密度圖不夠精確。可以根據經驗公式來獲得分組從而確定時間區間大小。區間分組的經驗公式為:

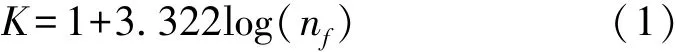
式中:nf是數組中故障數據的個數；K為分組數。

利用獲得的分組數進行分組，獲得故障間隔時間分組表，如表1所示。

表1 故障間隔時間分組表

表1中:tmax是故障數據采集獲得的最大時間值；k為分組數；ti-是分組區間的左端點；ti+是分組區間的右端點；是分組區間的中間值；ni是第i組內故障個數；fi是第i組內故障發生的頻率；為概率密度觀測值。的計算公式為:

式中:ni為每組故障間隔工作實踐中的故障頻數；n為故障總數；Δti為組距。

1.2 經驗分布函數法

用經驗分布函數法將故障數據處理，將故障間隔時間按照大小順序排列:t1≤t2≤…≤tn，為減小誤差，常用中位秩近似計算F( ti):

式中:i為故障數據的標號(1，2，…，n)；n為故障數據的總數。利用故障間隔時間ti作橫坐標，F ti()為縱坐標，繪制故障間隔時間分布函數的散點圖。

2 參數估計

通過對故障間隔時間分布密度函數散點圖以及故障間隔時間分布函數散點圖的繪制，可以初步確定分布函數所屬類型，進而使用最小二乘法[8]對所屬分布中的參數進行估計。基本思路就是將非線性問題轉化為線性問題，從而求出未知量。基本步驟:

假設有n個觀測值 (xi，yi)(i＝ 1，2，…，n)，如果x、y之間存在線性關系，即可以用直線來擬合x、y之間的關系。

其中，參數a，b的值為:

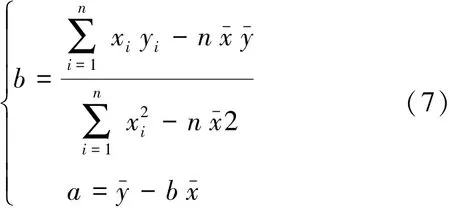
2.1 威布爾分布的參數估計

威布爾分布的函數表達式:

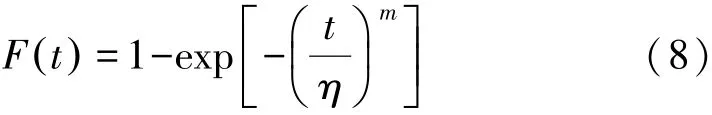
對于威布爾分布[9]可以將兩邊取自然對數，然后化簡可以得到，時間t如果服從威布爾分布，則{ln t，lnln[ 1/(1-F( t))]}服從線性關系，進而利用x＝ln t，y＝lnln[ 1/(1-F( t))]構造線性關系式:

從而求出未知量m、η。

2.2 指數分布的參數估計

指數分布的函數表達式:

也可以采用威布爾分布進行參數估計的方法，進而可以獲得{t，ln[1-F t()]}服從線性關系，可以利用x＝t，y＝ln[1-F t()]構造線性關系式:

從而求出未知量λ。

3 分布函數的擬合檢驗

在初步假設函數的分布類型后，需要對所屬分布進行檢驗，已確定假設的分布函數為正確的。這里使用χ2檢驗的方法，這種方法的基本原理是在于比較出理論頻數與實際頻數之間的差異，然后將用來接受檢驗的統計量χ2的觀測值與標準臨界值之間進行比較，來檢驗假設分布是否正確。

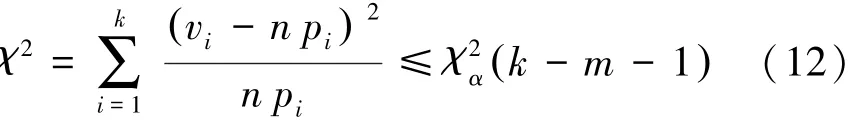
式中:n是樣本數量；k是分組數；m是未知參數的個數；α是顯著性水平；vi是第i分組的實際頻數；pi是第i分組理論頻率。

4 分布模型優選

根據假設檢驗過程，可能出現假設的幾種分布都正確的情況，對于哪一種分布更加符合實際的分布情況，這就需要對模型進行優選。經過了擬合檢驗，一般使用擬合優度值的比較來確定分布函數最終的選擇。擬合優度[10]一般使用R表示:

式中:yi是擬合值；是yi的平均值；是觀測值。

通過優度值的計算比較，就可以判斷函數所屬的分布類型，進而進行可靠性評估指標的計算，獲得相應的數值。

5 數控磨床冷卻系統可靠性指標計算實例

5.1 散點圖的繪制

現在將為期一年半的6臺MKS系列數控磨床的故障數據進行分類整理，獲得數控磨床冷卻系統故障數據27個。根據公式(1)計算得到分組 K＝1+3.322log27＝5.75，這里可以取6。數據采集采用定時截尾法，采集區間的最大時間值為14 664 h獲得故障間隔時間分組表，如表2所示。

組號 區間范圍 組中值 頻數 頻率 概率密度觀測值1 0～2 445 1 222.5 14 0.51 0.000 2 2 2 445～4 890 3 667.5 7 0.26 0.000 1 3 4 890～7 335 6 112.5 3 0.11 0.000 045 4 7 335～9 780 8 557.5 1 0.04 0.000 016 5 9 780～12 225 11 003 1 0.04 0.000 016 6 12 225～14 670 13 448 1 0.04 0.000 016

利用表2的組中值以及概率密度觀測值作故障間隔時間分布密度函數散點圖，如圖1所示。

利用故障間隔時間ti作橫坐標，F ti()為縱坐標，繪制故障間隔時間分布函數的散點圖，如圖2所示。

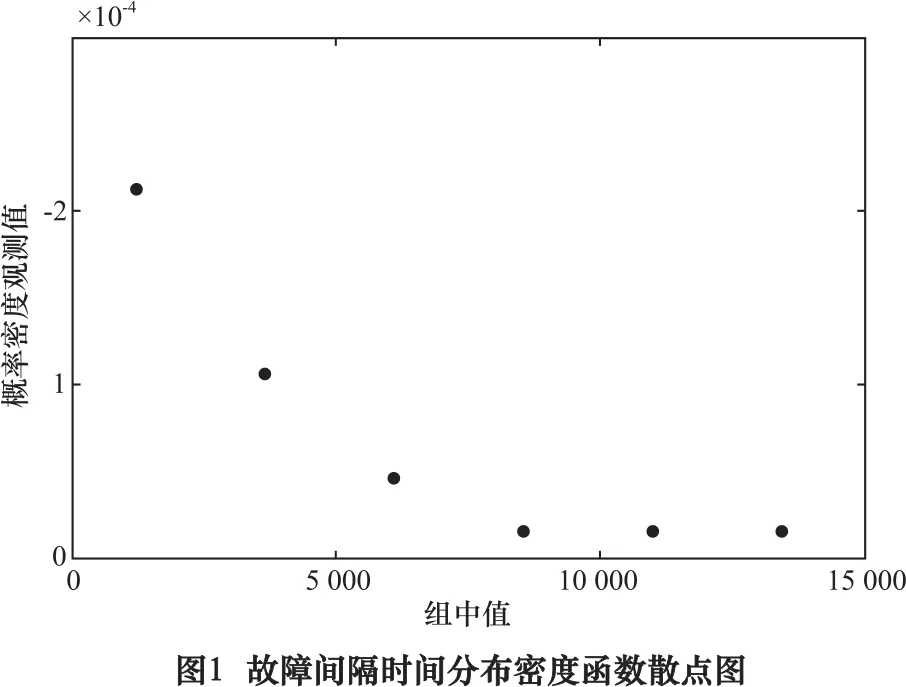
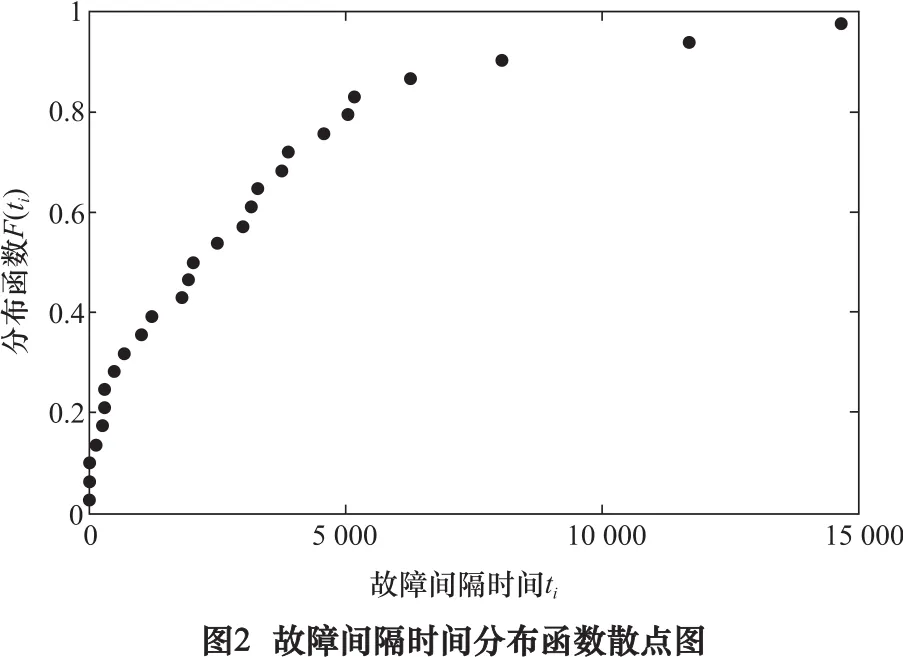
根據圖1和圖2可以假設分布函數屬于威布爾分布或者指數分布。

5.2 分布函數的參數估計

根據公式(8)和(9)計算出 m＝0.012 3，η＝596.530 3。分布函數屬于威布爾分布時的公式為:

根據公式(10)和(11)計算出λ＝0.000 3。因此分布函數屬于指數分布時的公式為:

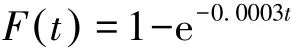
5.3 分布函數的擬合檢驗

使用χ2檢驗法檢驗兩種分布是否符合假設。利用公式(12)分別計算出威布爾分布和指數分布時的χ2值，與標準值進行比較。

(1)威布爾分布的擬合檢驗

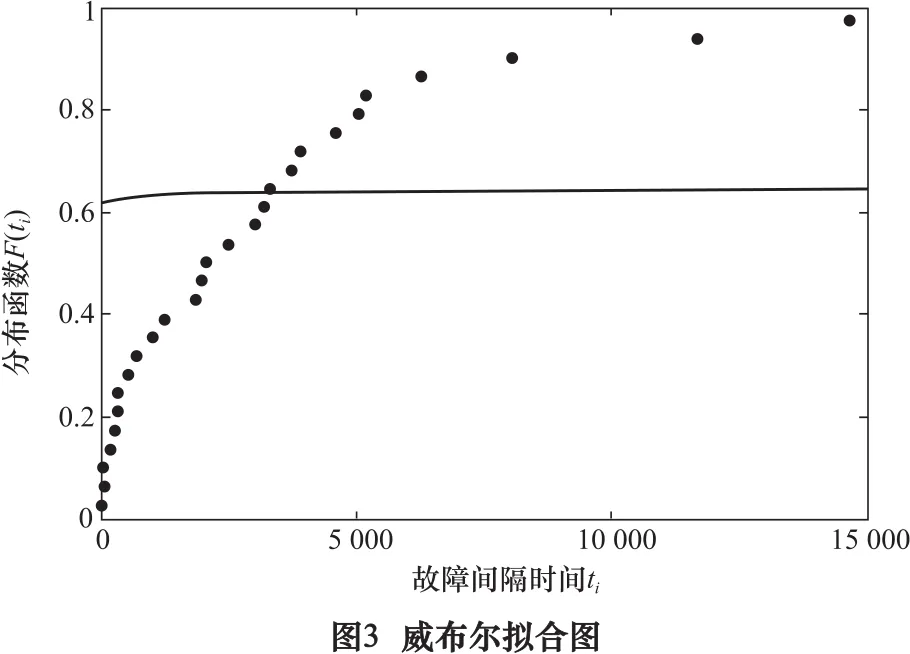
威布爾分布函數的表達式為:

其函數擬合圖，如圖3所示。

(2)指數分布的擬合檢驗

指數分布函數表達式為:

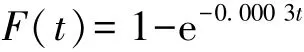
其函數擬合圖，如下圖4所示。

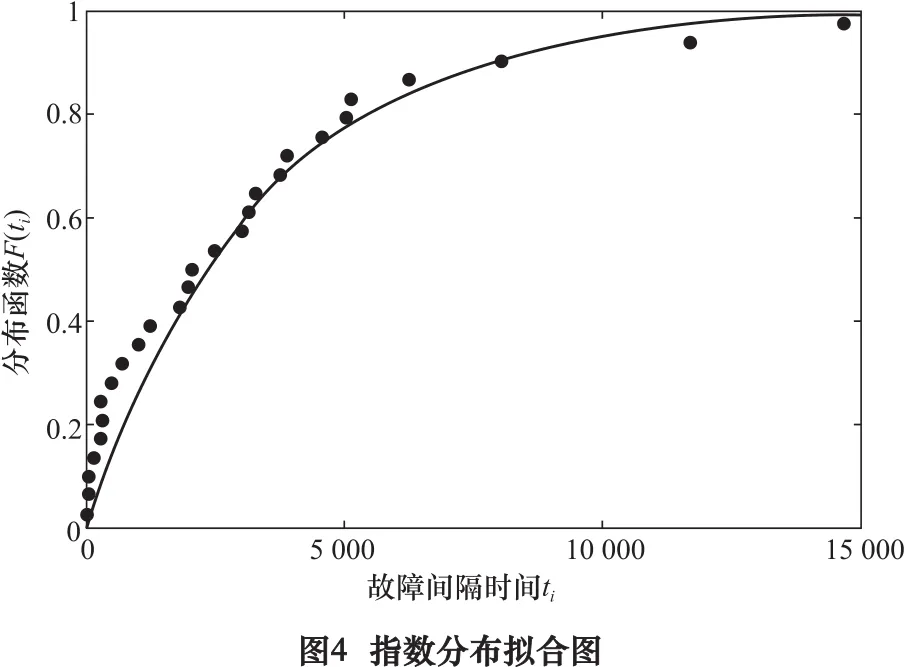
由此可見威布爾分布并不符合假設，假設不成立。指數分布屬于符合假設。因而可以得到故障間隔時間分布屬于指數分布。

5.4 可靠性指標的計算

根據上述計算得到的數控磨床冷卻系統的分布可以進行相關的可靠性指標計算[11-14]，可以得到數控磨床冷卻系統的故障間隔時間符合指數分布，且指數分布的表達式為:

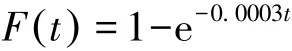
(1)平均故障間隔時間

平均故障間隔時間(MTBF)是指在設備發生一次故障到下一次故障間的平均工作時間。在已知設備故障間隔時間分布概率密度函數f t()的情況下，平均故障間隔時間MTBF:

由于故障間隔時間分布符合指數分布，且表達式為F t()＝1-e-0.0003t，因此可以得到故障間隔時間分布概率密度函數f(t)的表達式為:

進而計算冷卻系統的平均故障間隔時間(MTBF):

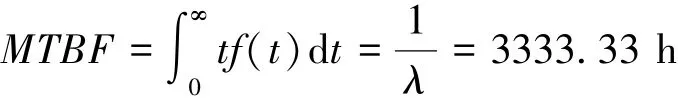
(2)平均維修時間

平均維修時間(MTTR)是指從故障到維修完成所用時間的平均值。

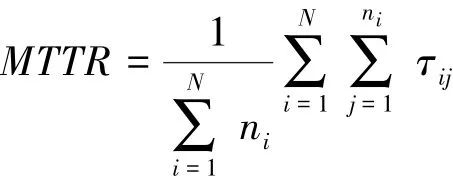
式中:N是測試的產品總數；ni是第i個測試產品的維修次數；τij是第i個產品從第j次維修所用的時間。

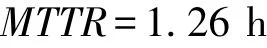
(3)固有可用度

數控磨床的可用性水平是反映設備能工作時間以及設備服務時間之間的比值，是可靠性與維修性的綜合反映。固有可用度A是指在規定的使用條件下，數控磨床保持其規定功能的概率:

由此可見數控磨床冷卻系統的可用性比較高，有效工作程度較高，具有較好的綜合功用。

6 結語

通過對工廠采集到的故障數據進行分析，對數控磨床的子系統——冷卻系統進行了詳細分析與指標評估。對數控磨床冷卻系統的故障間隔時間進行分組，繪制其分布函數散點圖以及分布密度函數散點圖，利用參數估計和分布檢驗計算并確定故障間隔時間的分布為指數分布，并且得到分布函數表達式。利用分布函數的表達式分別計算了數控磨床冷卻系統的平均故障間隔時間MTBF為3 333.33 h，平均維修時間MTTR為1.26 h以及固有可用度A為0.999 6。以上計算的結果已經反饋到生產廠家得到了認可，并應用到后續可靠性提升的工程當中。