航天剛-彈-液耦合系統的彈-液耦合研究

梁立孚， 郭慶勇

(哈爾濱工程大學 航天與建筑工程學院， 哈爾濱 150001)

隨著航天事業的發展，特別是大型空間站的建立、空間實驗室的出現以及探討人類長期在宇宙空間居住或者旅行的研究工作的開展，較全面地研究剛-彈-液耦合動力學的任務已經提上了日程[1-2]。

作為一個航天大國，中國學者在航天充液系統的剛-彈-液耦合機理研究和大規模剛-彈-液耦合模型建模計算的應用研究方面，已經進行了一些有益的探索，并且取得了豐碩的研究成果。杜建鑌和王勖成[3]針對具有旋轉周期性的含液容器，將旋轉周期方法引入液固耦合動力特性分析，開發出一套有效的液固耦合有限元分析方法。劉習軍等[4]研究了殼液耦合系統的自激振動問題和重力波現象。馬興瑞等[5]將流固耦合問題作為一個專題進行了研究。邢景棠、周盛和崔爾杰[6]全面綜述了流固耦合力學及其特點、研究分支、一些進展及進一步發展，并重點闡述了國外學者在這一學科領域的研究成果。王勖成[7]研究了流固耦合的有限單元法，采用一種簡化的方式處理彈-液耦合問題。李磊等[8]研究了運動圓筒內液體流動不穩定的非線性特征。席如青和曲廣吉[9]研究了充液航天器任意旋轉對稱偏置貯箱在低微重力情況下的小幅液體晃動問題, 并編制了具有工程實用性和通用性的計算機分析軟件。李英波和馮正進[10]建立了三軸定向充液衛星在二維平動和二維擺動擾動作用下的空間擺等效力學模型。王佳棟等[11]研究了帶有環形剛性隔板的部分充液剛性圓柱罐中液體的微幅晃動特性。黃華等[12]建立了三維質心面等效模型, 將貯箱內液體等效為位于液體質心處的質點。賀元軍等[13]建立了在微重力環境、橫向激勵下圓柱貯箱液固耦合系統的動力學方程，并得到了耦合系統的幅頻特性曲線。包光偉和王政偉[14]通過建立液體晃動特征問題的泛函極值原理, 計算了平放圓柱腔內三維液體晃動的特征頻率, 并與解析解、實驗結果和二維有限元數值解進行了比較。陳建平等[15]提出了剛-彈-液耦合系統的液體-多體耦合力學模型。高索文等[16]分析了俯仰激勵下矩形貯箱類液固耦合系統動力學特性。茍興宇等[17]研究了彈簧-質量系統與圓柱貯箱類液體有限幅晃動系統間的非線性耦合動力學問題, 在建立了六自由度非線性耦合動力學模型的基礎上, 導出了液體有限幅晃動力和力矩解析表達式, 說明在終了構形上積分及壓力表達式中的非線性項是有限幅晃動作用力、作用力矩非線性的根源。李青等[18]分別綜述了國內外學者在充液航天器液體晃動和液固耦合動力學方面的研究進展，并重點闡述了國外學者在這一學科領域的研究成果。

在剛-彈-液耦合動力學中，存在剛-彈耦合、剛-液耦合、彈-液耦合，它們是互相聯系和相互影響的。筆者分別研究了非線性剛-彈耦合動力學[19]和剛-液耦合動力學[20]，為研究剛-彈-液耦合動力學中存在的剛-彈耦合、剛-液耦合提供了重要的參考。在此基礎上，還研究了剛-彈-液耦合動力學[21]， 但是沒有專門研究彈-液耦合問題。所以，本文重點研究剛-彈-液耦合動力學中的彈-液耦合問題，這是一個關系到航天充液系統液固耦合機理研究和大規模液固耦合模型建模計算研究方面的重要問題。

1 剛-彈-液耦合中的剛-彈耦合、剛-液耦合和彈-液耦合特點

設有如圖1所示的剛-彈-液耦合系統。文獻[21]給出了剛-彈-液耦合動力學一類變量的Hamilton型的擬變分原理，這里給出一類變量的Hamilton型的擬變分原理改進形式為(用實體張量符號書寫)

δπreq-δQreq=0

(1)

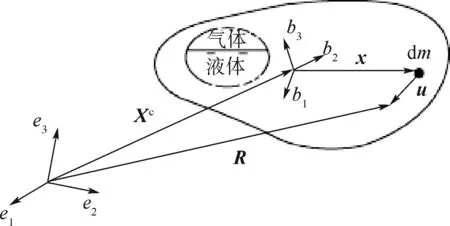
圖1 參考標架Fig.1 Frame of reference

式中：

(2)

(3)

(4)

(5)

先決條件為

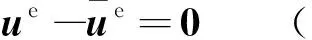
(6)

該變分原理的泛函隱含彈-液耦合，這是因為彈-液耦合是在彈-液交界面處出現的[6]，在彈-液交界面處，按照一般的力學原理，位移滿足協調關系，應力滿足平衡關系，這便是剛-彈-液耦合中的彈-液耦合的特點。因為這一問題的重要性，將在第2節結合研究彈-液耦合的機理，做進一步的說明。

2 剛-彈-液耦合動力學中彈-液耦合的機理

對于剛-彈-液耦合系統而言，彈-液交界面是整個系統內部出現的。假想將彈-液耦合體劃分為2個元素，其彈-液交界面Sw是無際邊界(inter-element boundary)[23-24]，無際邊界條件為

ue-uq=0(在Sw上)

(7)

應用錢偉長先生倡導的Lagrange乘子法[23，25]來處理無際邊界條件的問題。為此，將式(1)寫成展開形式，引入Lagrange乘子λ，將無際邊界條件式(7)納入泛函中，可得

(8)

其先決條件為式(6)。

進行分部積分，可得

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

應用Green定理，可得

δuedV

(21)

(22)

(23)

將式(9)～式(23)代入式(8)的變換式中，考慮到位移邊界條件的變分式為δue=0，并且按慣例在時域邊界t=t0和t=t1處取δXc、δθ、δue、δuq等于零，可得

(24)

由于δXc、δθ、δue、δuq和δλ的任意性，故由式(24)可得擬駐值條件為

(25-1)

(25-2)

(25-3)

ne-Te=0(在Sσ上)

(25-4)

ue-uq=0(在Sw上)

(25-5)

ne+λ=0(在Sw上)

(25-6)

λ=0(在Sw上)

(25-7)

(25-8)

nq-Tq=0(在Sf上)

(25-9)

由式(25-6)和式(25-7)解得

(26)

(27)

分析式(26)和式(27)的物理意義。不難看出，式(26)表示在Sw處彈性體所承受的應力，式(27)表示在Sw處液體所承受的應力。并且式(26)和式(27)都與經典分析力學中Lagrange乘子是約束力的論述相吻合。將式(26)代入式(27)，或者將式(27)代入式(26)，均可得到

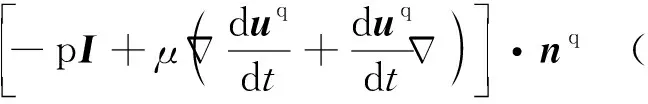
(28)

認為彈性體和液體以無際邊界面為接觸面，二者在此處相互作用，式(28)的物理意義可以解釋為：在無際邊界Sw處，彈性體對液體的作用力和液體對彈性體的作用力大小相等，方向相反。

式(28)又可寫為另一種形式：

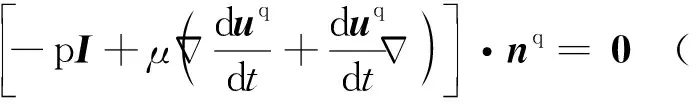
(29)

認為彈性力和液體力共同作用在無際邊界Sw處的無限薄的一層物質面上，式(29)表明：由于剛-彈耦合動力學導致的應力和由于剛-液耦合動力學導致的應力在無際邊界面Sw處構成平衡應力系。

在以上分析中，建議注意：在無際邊界面Sw處，ne+nq=0。

剛-彈-液耦合動力學的擬變分原理式(8)的豐富的內涵反映在其駐值條件中：駐值條件式(25-6)和駐值條件式(25-7)經變換得到式(29)，反映彈-液耦合的力的平衡關系；駐值條件式(25-5)反映彈-液耦合的位移協調關系；這是本文的主要研究內容。駐值條件式(25-3)和駐值條件式(25-4)反映剛-彈耦合特性；駐值條件式(25-8)和駐值條件式(25-9)反映剛-液耦合特性；駐值條件式(25-1)和駐值條件式(25-2)反映連續介質動力學對剛體動力學的影響。由如上論述可以看出，剛-彈-液耦合中彈-液耦合的平衡方程式(29)中的變量，不僅受到彈-液耦合的影響，還受到剛-液耦合(式(25-8)、式(25-9))和剛-彈耦合(式(25-3)、式(25-4))的影響。反之，剛-液耦合(式(25-8)、式(25-9))和剛-彈耦合(式(25-3)、式(25-4))的變量，也要受到彈-液耦合式(29)的影響。

綜合以上分析，可以明確剛-彈-液耦合動力學中彈-液耦合的機理。剛-彈-液耦合動力學中彈-液耦合發生在彈、液兩相的無際邊界面上, 在該邊界面上，位移滿足協調關系式(25-5)，應力滿足平衡關系式(29)。

應當注意到，雖然剛-彈-液耦合動力學中彈-液耦合是在彈-液交界面實現的，但是，彈-液耦合是受到控制方程式(25-1)～式(25-9)的制約的。

3 彈-液耦合機理與建模計算相結合

關于彈-液耦合的建模計算研究，首先會想到有限元建模計算問題。

結合第2節的研究，由擬駐值條件式(25-5)可以看出，通過應用Lagrange乘子法，已經將無際邊界條件轉化為泛函的擬駐值條件；從有限元建模計算方面考慮問題，這一研究進展實現了從協調元(compatible model)到雜交元(hybrid model)的過渡。國外學者應用Lagrange乘子法研究有限元素法基本上到此為止。

按照中國著名應用數學和力學專家錢偉長院士的理論，還要在上述研究的基礎上，進一步識別Lagrange乘子，即將Lagrange乘子用泛函中原有的變量來表示，然后將已經識別的Lagrange乘子代入泛函中，用來減少有限元素法的計算自由度。

將Lagrange乘子的表達式(26)代入泛函式(8)中，可得

(30)

應用與第2節相同的方法，不難求得，其駐值條件為

(31-1)

(31-2)

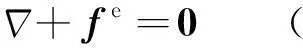
(31-3)

ne-Te=0(在Sσ上)

(31-4)

ue-uq=0(在Sw上)

(31-5)

(31-6)

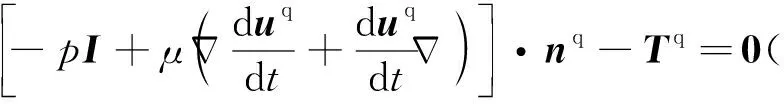
(31-7)

比較式(31)和式(25)可以發現，識別Lagrange乘子之后，可以減少計算自由度。具體地說，式(25)和式(8)的Lagrange乘子尚未識別，它們仍然作為計算自由度存在于控制方程中；由于這里的Lagrange乘子λ是矢量，需要計算其3個分量方可確定，即其占用3個計算自由度。式(30)和式(31)的Lagrange乘子已經識別，即Lagrange乘子已經應用泛函中原有的變量表達出來，從而減少3個計算自由度。注意到，這是將剛-彈-液耦合系統劃分為彈性體和液體2個元素，來處理其無際邊界條件問題得到的結果。在有限元建模計算中，彈-液交界面可以離散為很多個元素的無際邊界面，因此明確彈-液耦合機理之后，可以有效地減少計算自由度。具體地說，假設彈-液交界面可以離散為100個元素的無際邊界面，根據前面的分析，明確彈-液耦合機理之后，可以減少300個計算自由度。

再引申一步，在有限元建模中，除了以彈-液交界面作為元素的無際邊界面之外，還有更多的元素的無際邊界面不是彈-液交界面，它們也存在用識別Lagrange乘子法減少計算自由度的問題。這樣一來，減少的計算自由度就更多了。結合以上2種因素，可以大大減少計算自由度。這是中國學者對應用數學和力學的一大貢獻。

最后說明，在剛-彈-液耦合動力學的建模計算研究中，存在彈-液交界面處的無際邊界條件。把彈-液交界面處的無際邊界條件處理好了，其余部分的有限元建模計算與一般的有限元建模計算便沒有多大差別了，也就比較容易處理了。二者相結合，便是一個比較完整的剛-彈-液耦合動力學的建模計算研究。對于如何實現有限元計算的問題，可以參閱著名流固耦合專家英籍華人學者邢景棠先生的近期著述[26]。

4 結 論

航天剛-彈-液耦合動力學是航天器動力學領域最具有挑戰性的研究方向之一。

1) 通過分析剛-彈-液耦合動力學擬變分原理的泛函，說明了剛-彈耦合、剛-液耦合和彈-液耦合的特點。

2) 通過識別Lagrange乘子，逐步說明了彈-液耦合的機理。

3) 通過分析識別Lagrange乘子前后泛函的駐值條件，明確了識別Lagrange乘子可以有效地減少計算自由度。

研究工作處于該研究方向的理論基礎層面，具有較好的理論意義，對這類系統有限元建模、計算及結果分析、討論具有重要的參考價值。