航空發動機轉子結構布局優化設計方法

李超， 金福藝， 張衛浩

(北京航空航天大學 能源與動力工程學院, 北京 100083)

目前，中國航空燃氣渦輪發動機的研制正處于從測繪仿制到自主研發的過渡發展階段，由于對結構設計的基礎理論研究不足，在設計上大多依賴于傳統的工程設計經驗。而對于一臺高性能、高可靠性的航空發動機來講，單純依靠長期積累的設計經驗或測繪仿制不能滿足其先進性的需求。所謂布局優化設計，即是結構構型的合理設計，只有合理的構型設計才可能最大程度的滿足結構效率[1]的要求。布局設計在飛行器外形[2]、建筑[3]、橋梁[4]和經濟[5]等領域已經有著較為深入的研究，但是對航空發動機結構的布局設計，國內外均鮮有報道。目前，對于航空發動機轉子系統的研究多集中在轉子動力學特性的計算方法[6-7]，探索轉子力學機理，研究影響其力學特征的關鍵因素[8]，但是實際工作轉子結構型式通常較為復雜，影響因素繁多，很難在工程中得到較好的應用，特別是在航空發動機領域，很難大幅度地對轉子結構進行改進和優化設計。

鑒于此，本文以典型高推重比渦扇發動機高壓轉子的結構構型為例，探索了航空發動機轉子結構布局優化設計的方法流程。首先，對各設計變量進行參數關聯性研究，對各個待優化的構型參數對結構力學特性的敏感度進行統計分析；然后，在此基礎上對結構的構型進行基于響應面的布局優化設計；最后，通過隨機驗證點充分驗證優化結果的準確性。本文方法可以為結構改型提供指導方向，較大程度地擺脫轉子結構的經驗設計。

1 結構布局優化設計的定義及算例模型

結構布局設計是指基于某些數學優化算法使能夠自動識別系統中構型參數的最優或次優布置的技術，由此充分展示結構構型所帶來的力學特征的變化。簡言之，即是通過建立轉子構型和其力學特征之間的關聯性，進而揭示結構構型和尺寸效應所引起的力學特性的變化，同時附加先進的優化算法，實現轉子結構與力學特征一體化設計。結構布局設計可以為航空燃氣輪機總體結構初始設計階段進行結構構型和尺寸控制，提供設計指導的理論依據。本文以典型的高推重比渦扇發動機高壓轉子結構為例，論述布局優化設計的流程、布局設計方法的可靠性及布局設計的重要意義。

結構布局優化設計可以為結構改型提供指導。圖1為2種典型的高推重比渦扇發動機高壓轉子結構，二者均為1-0-1支承方案。結構Ⅰ為7級壓氣機和1級渦輪，前2級壓氣機為懸臂結構，靠近渦輪處存在一個封沿盤。結構Ⅱ為5級壓氣機和1級渦輪，無懸臂結構，封沿盤靠近壓氣機。通過這2種典型結構構型，可以衍生出其他類型高壓轉子結構。例如，同結構Ⅰ相比，F110高壓轉子總體上是將壓氣機增加2級，并在壓氣機后增加封沿盤；結構Ⅱ則是不存在懸臂的一類結構。以上這些轉子結構的改型設計均可以在布局優化設計中得到完整的體現。當然，每家航空發動機集團公司在結構方案的選擇上都有著較強的繼承性，有著各自不同的設計風格。在布局優化設計時，應充分考慮傳統工程經驗和技術的積累，在此基礎上進行布局的優化設計，這一點在布局設計中是需要充分考慮的。

圖1中，實線勾勒出了轉子大概的結構布局線路，盤和葉片等轉子構件按照一定的規則分布其上，實心圓點代表構件的集中質量。值得注意的是，轉子的結構布局優化設計是對整體構型進行優化設計，并不涉及具體構件的尺寸設計。例如，渦輪盤的構型屬于強度設計問題，不在轉子結構布局設計范疇。

圖1 典型轉子結構Fig.1 Typical rotor structure

目前，轉子的力學特性計算多為傳遞矩陣法及有限元法，考慮到傳遞矩陣法程序的通用性和可擴展性均較差，較難在工程中廣泛使用，本文優化示例過程均采用有限元法進行計算，所建立的有限元模型如圖2所示。盤和葉片的等效分布質量和轉動慣量已經加到相應的位置處(mass21單元)，如圖2中的A、B、C、D、E、F、G所指。前、后支承位置在抗變形能力優化設計時為簡支約束，在力學環境適應能力優化設計時采用彈性支承(combin214軸承單元)，其支承剛度如表1所示。其余構型全部采用三維實體solid189高階單元，不計阻尼。

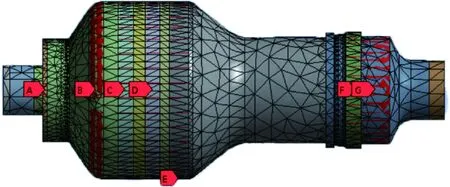
圖2 有限元模型Fig.2 Finite element model

表1 支承剛度Table 1 Supporting stiffness107 N/m

2 關鍵特征參數及其確定方法

關鍵特征參數的探索是布局設計的首要任務。所謂關鍵特征參數，是指對轉子的力學性能(剛度特征和模態特征等)具有明顯影響的構型參數。由于很難把握構型參數相互之間的約束規律，對全體構型參數進行優化設計是不現實的，同時，在后續試驗設計(DOE)研究中，設計點的數量會隨著輸入參數的數量增加而迅速增加，嚴重降低DOE計算效率。因此，首先需要以一個較優的轉子構型參數為基礎(可直接由工程實際確定)，對各個參數之間進行關聯性研究，確定對轉子力學性能有明顯影響的關鍵特征參數。圖3為轉子結構布局的構型尺寸工程圖，由于結構的構型尺寸及約束條件參數繁多，圖中僅標出了待優化的部分參數。其中，A1為前軸頸與水平線的傾角，R1為其倒角半徑；A2為中間軸段與水平線的傾角，R2為其倒角半徑，為方便敘述，各構型參數在本文里均用其代號表示，對應位置已標于圖3中。原始構型參數歸納如表2所示。

統計學中的參數關聯性研究有多種方法[9-10]，已廣泛應用于優化設計。本文通過拉丁超立方(Latin hypercube)法布置樣本點，使用斯珀曼(Spearman)法進行數據之間的關聯性分析。斯珀曼法是在基于蒙特卡羅關系下，檢查2個變量之間的單調關系，比線性關系限制較少，具有較高的準確度。通過該方法從眾多構型變量中選出較少的參數作為關鍵特征參數，這些參數也是后續待優化的設計變量。

得到關鍵特征參數的目的之一是進行DOE[11]。DOE是研究正確的設計試驗計劃，分析試驗數據的理論和方法，通過改變過程的輸入因素，觀察其相應的輸出響應變化，從而獲取關于此過程的知識，確定各個輸入因素的重要性以及各輸入因素如何影響輸出響應，并如何達到最優化的目的。DOE類型分為很多種，常見的如稀疏網格設計[12]、Box-Behnken試驗設計[13]、田口靜態試驗設計[14]、拉丁超立方試驗設計[15]等。DOE是獲取響應面的前提條件，合適的DOE方法不僅可以提高計算效率，而且可以有效提高響應面的擬合精度。為了最大程度提高響應面擬合精度，本文采用稀疏網格響應面法。稀疏網格響應面是一種自適應響應面，可以對數據點進行自動細化，精度很高。當然，每一次細化都需要對構型參數改變的有限元模型進行重啟動分析，這是以犧牲計算效率為代價的。

轉子系統結構效率[16]內容主要包括承載能力、抗變形能力和力學環境適應能力三方面。承載能力屬于強度優化設計，不屬于布局優化設計范疇。布局優化設計主要是針對轉子系統的抗變形能力和力學環境適應能力進行構型的尋優設計。由于本文目的僅為闡述轉子結構布局優化設計的方法、方法可靠性和重要意義，不針對某型號的發動機轉子，不針對具體的工程結構，另外考慮到優化過程中，為了便于尋找各構型參數對某個力學特征是否存在影響及影響的程度，因此本文將抗變形能力的尋優目標參數只定義了慣性載荷下的最小等效剛度，力學環境適應能力的尋優目標參數只定義了一階彎曲共振時的轉子轉速，同時兼顧總質量的變化情況。本文給出了工程綜合仿真示例。值得注意的是，尋優目標參數應該在結構效率的定義范圍內，需要依據實際情況而變化。

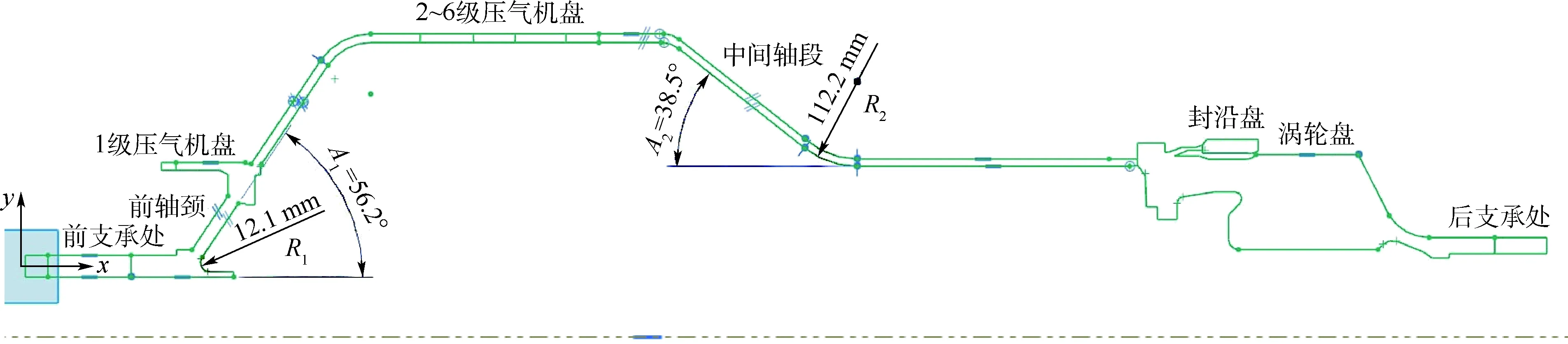
圖3 布局尺寸Fig.3 Layout size

表2 待優化的原始構型參數Table 2 Original configuration parameters for subsequent optimization

3 基于響應面法的結構布局優化設計方法流程

航空發動機轉子系統結構布局優化設計方法流程如圖4所示。

步驟1建立原始CAD參數化模型，并初步判斷對結構力學特征有明顯影響的構型參數作為待優化的設計變量，這是依據技術積累和工程經驗得出的。建立模型時應注意圖形元素之間的約束條件，避免構型參數改變時，轉子結構模型的嚴重失真，否則將導致結構布局優化設計的失敗。

步驟2建立有限元模型，進行有限元求解，指定優化目標(如結構效率相關評估參數)，將有限元求解器與CAD關聯。這里主要是為了使構型參數改變時，利用CAD快速建模和利用有限元求解器快速求解，以期實現迭代計算。

步驟3參數關聯性分析，確定關鍵特征參數。從步驟1選取的待優化設計變量中，進一步確定哪些是對力學特征有顯著影響的構型參數，作為關鍵特征參數，這是后續優化迭代中的設計變量。

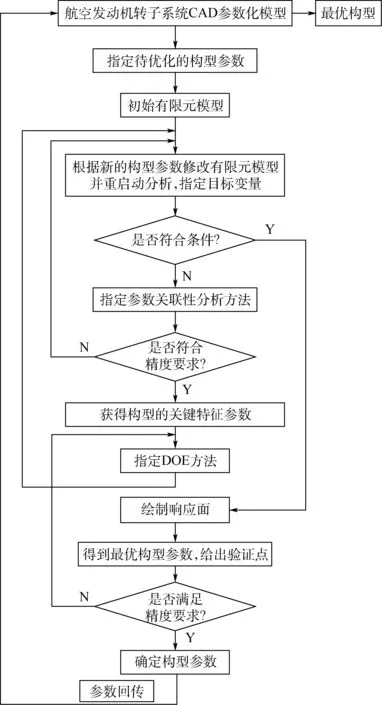
圖4 結構布局優化設計方法流程Fig.4 Flow of structure layout optimization design method

步驟4進行DOE，繪制響應面。確定響應面的擬合優度，確保數據的準確性。

步驟5基于某些數學優化算法，找到最優或次優的構型參數。

步驟6與原構型對比，驗證優化結果。

4 基于結構效率的結構布局優化設計

為了充分證明航空發動機轉子系統結構布局優化設計方法的可行性，本節以典型高推重比渦扇發動機高壓轉子構型(見圖3)為例，分別從抗變形能力和力學環境適應能力兩方面對轉子結構進行結構布局優化設計。構型參數波動的上下限均為在原始構型的基礎上±10%。

4.1 抗變形能力

根據航空發動機轉子系統的結構特征，在設計中對轉子系統抗變形能力的要求有：①具有良好的橫向彎曲剛度；②盤軸連接處具有良好的角向剛度。在轉子系統剛度設計中，常采用的大比剛度材料有利于提高結構的抗變形能力，但是材料的選取通常根據強度設計準則來確定，對于給定的材料，通過轉子軸截面結構形狀和面積的優化，可以進一步提高轉子系統的剛度，從而達到提高其抗變形能力的目的。雖然連接結構處存在的剛度損傷，對轉子結構的力學特征存在較大影響，但是由于其力學特征計算的復雜性，在結構構型設計初期的布局優化中一般不予考慮。

為此，對轉子結構橫向施加1個重力加速度，此時轉子將發生彎曲變形，計算整體轉子結構橫向變形的最大值(TD_Max)和轉子結構的質量(TM)，通過尋找合適構型的設計參數，使得最大變形量和總質量最小。

基于斯珀曼[17]法的參數關聯性分析(進行了100組構型參數計算)可以得到如表3所示的各參數間的相關性矩陣，繪制出相應的參數關聯性云圖，如圖5所示，其中顏色的深淺表示關聯度的強弱。

從圖5中可以較為清晰地看出各參數之間的關聯性強弱，嚴重影響最大變形量(即轉子結構的抗變形能力)的參數為高壓轉子構型參數A2，對最大變形量的線性關聯系數為0.998 7，對總質量線性關聯系數為-0.954，均接近1，明顯高于其他值。其次，構型參數R1和R2的變化對總體質量稍有影響。綜上，可以初步斷定，對轉子系統抗變形能力具有顯著影響的關鍵特征參數為A2。

為了減少設計變量個數，略去一些對力學特征影響不敏感的參數，同時兼顧對實際轉子力學特征的影響。因為2個倒角半徑(R1和R2)只對結構質量有少許影響，且影響程度大體相當，因此將這2個構型參數一起去掉。接下來只研究2個錐角(A1和A2)的變化對轉子系統的抗變形能力和總質量的影響程度。

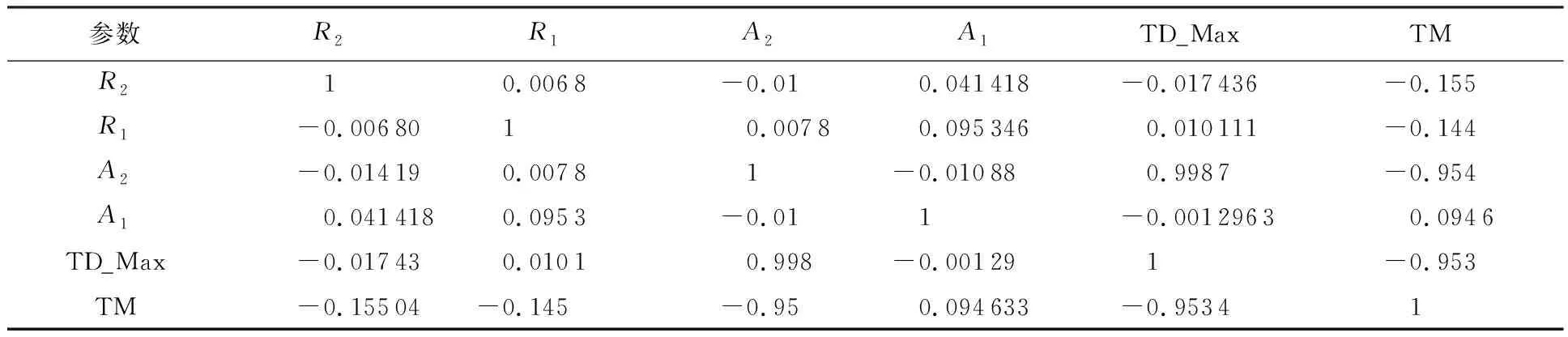
表3 抗變形能力優化相關性矩陣Table 3 Correlation matrix of anti-deforming ability optimization

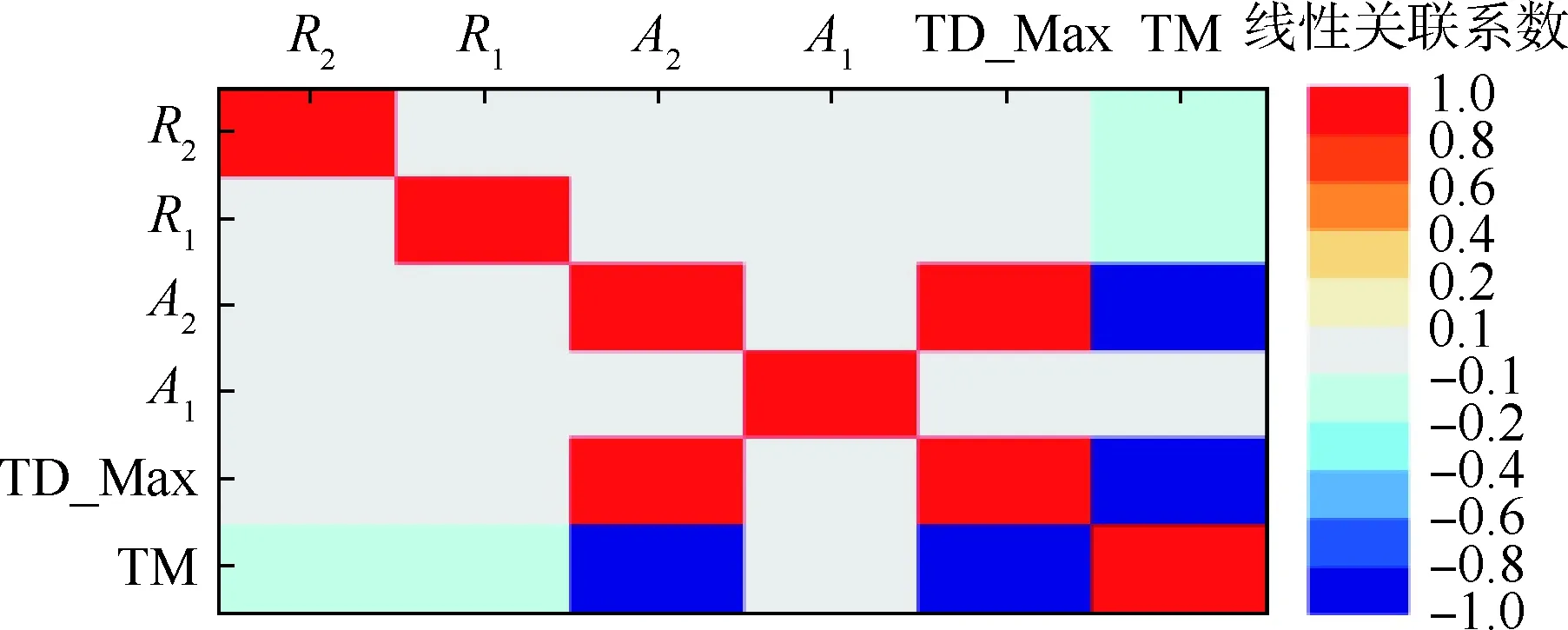
圖5 抗變形能力優化參數關聯性云圖Fig.5 Contour of parameter correlation about anti-deforming ability optimization

通過有限元迭代計算，可以得到總質量和最大變形量相對于2個錐角(A1和A2)的稀疏網格響應面，如圖6所示。

從響應面可以直觀地找出使最大變形量和總質量最小時所對應的構型參數。圖6(a)所示的最大變形量相對于2個錐角的響應面有著很高的“尖點”，存在迅速上升或下降的最大值點，一定程度上可以反映出，假如構型參數選取的不合理，可能會對轉子系統的力學特性產生嚴重影響。為了驗證響應面的準確性，給出了5個驗證點，如表4所示。

從隨機選取的5個驗證點所統計出的相對誤差來看，該響應面擬合度很高，幾乎零誤差，可以為下一步優化提供數據支持。響應面擬合程度的優劣直接影響后續優化結構，影響結構的可靠性，若誤差統計數據存在較大的值，則應以更多的數據點對響應面進行細化，直到誤差在允許的范圍內為止。

通過響應面的優化是基于某些先進算法實現，如多目標遺傳算法[18]、自適應多目標[19]等，相比于有限元計算耗時很少。遺傳算法是一種通過模擬自然進化過程搜索最優解的方法,在優化方法中具有獨特的優越性，通過前面得到的響應面，基于多目標遺傳算法最終得到3組候選設計點，如表5所示，表中“☆”表示優化后總質量最小的一組參數。

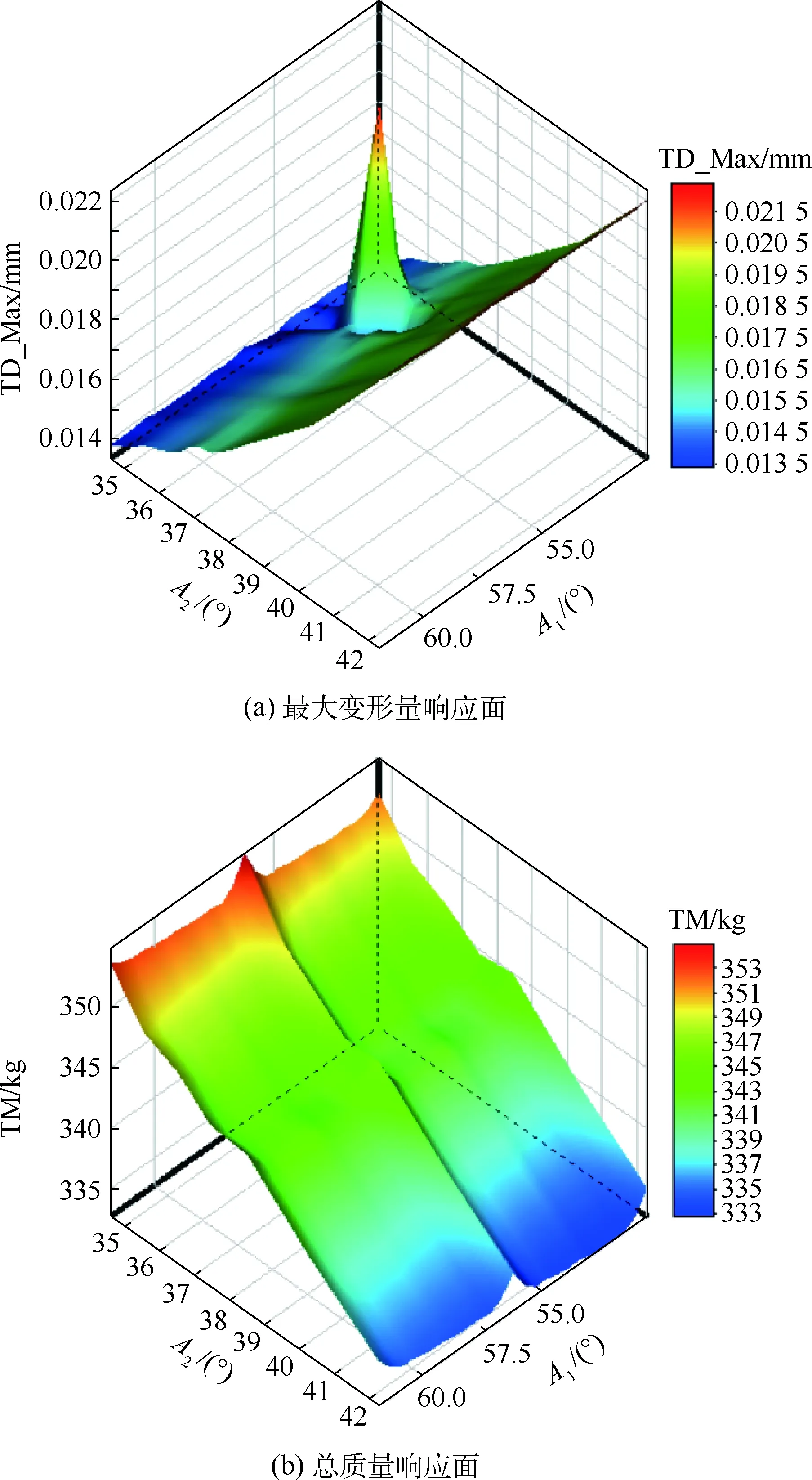
圖6 抗變形能力優化響應面Fig.6 Response surface of anti-deforming ability optimization

從表5可以看到，若以最大變形量最小為優化目標，應選擇第3組構型參數，即A1=50.646°，A2=37.806°，此時具有較強的抵抗慣性載荷的能力。若以總質量最小為優化目標，應選擇第1組構型參數，即A1=51.278°，A2=38.531°。若折中選取，則應選擇第2組構型參數。從表5中的數據也可以發現，雖然前后錐角僅有1°左右的變化，卻可以引起最大變形量和總質量的顯著改變，特別是質量的變化，大約4 kg。

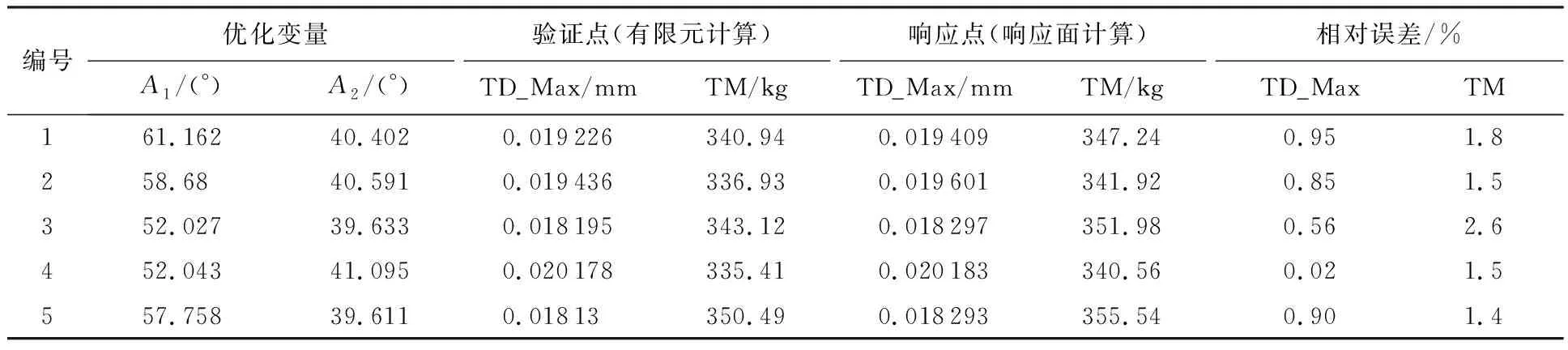
表4 抗變形能力響應面誤差驗證Table 4 Error verification of response surface of anti-deforming ability

表5 抗變形能力優化設計結果Table 5 Design results of anti-deforming ability optimization

考慮第1組誤差較小，若選取第1組設計點，與原始構型對比，質量減少3.59 kg，在慣性載荷作用下，最大變形量減少0.004 913 mm，如圖7所示。值得注意的是，本算例計算的是在1個重力加速度下的變形量，若在更大的慣性載荷作用下，優化效果會更加明顯。

由此可得，經過結構布局優化設計后的轉子結構，在慣性力下的最小等效剛度為

優化前的等效剛度為

優化前后相比提高了4.4×107N/m，整體提升了近28%的慣性剛度，可見轉子結構布局優化設計的顯著效果。

4.2 力學環境適應能力

轉子系統的工作轉速相對于共振頻率之間的穩定裕度一直是結構設計需要考慮的重要問題，在航空發動機轉子結構設計初期，常因為結構布局設計的不合理而達不到裕度要求(一般為20%)。例如，高壓轉子在工作轉速范圍內往往存在2個共振轉速，較低的共振轉速是由靜不平衡引起的，較高的共振轉速是由力偶不平衡引起的。工作轉速距離較近的一階彎曲振型和俯仰振型均應有一定的裕度，這就需要將一階彎曲共振頻率最大化設計。工程上一般通過調節支承處剛度來調節共振轉速，但若是構型設計嚴重不合理，單憑調節支承剛度是達不到要求的。

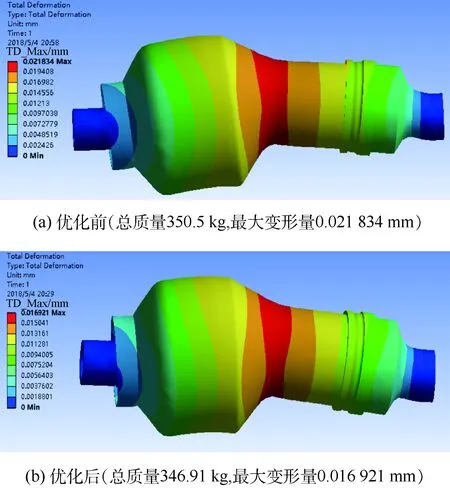
圖7 抗變形能力優化前后對比Fig.7 Comparison of results before and after anti-deforming ability optimization

仍以圖3所示的高壓轉子結構構型為例，以一階彎曲共振頻率最大、振幅最小且結構總質量最小為優化目標，通過對4個構型參數(見表2)的選取使結構趨于“合理化設計”。結構布局優化流程同第3節，基于斯珀曼法可以得到參數關聯性矩陣(見表6)及對應的云圖(見圖8)，觀察可知，關鍵特征參數依舊是A1和A2。

通過有限元迭代計算，可以得到結構總質量、一階彎曲臨界轉速和一階彎曲共振最大變形量相對于2個錐角(A1和A2)的稀疏網格響應面，如圖9所示。

表6 力學環境適應能力優化相關性矩陣T說able 6 Correlation matrix of mechanical environment adaptability optimization

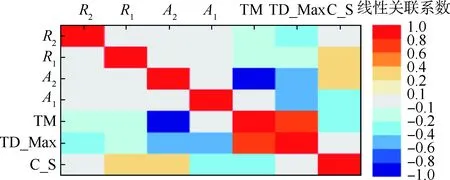
圖8 力學環境適應能力優化參數關聯性云圖Fig.8 Contour of parameter correlation about mechanical environment adaptability optimization

響應面誤差驗證如表7所示。可以看出，響應面誤差較小，擬合精度較高，可以為后續優化提供數據支持。基于多目標遺傳算法，最終得到了3組候選設計點，如表8所示。

從表8可以看到，優化結果誤差較小，第2組設計點的總質量和轉子在一階彎曲共振時的最大變形量較小，第3組的一階彎曲臨界轉速最大，可以考慮選擇這2組設計點。若選擇第3組為設計點，優化前后臨界轉速如圖10所示。

可以看出，相比于優化前，一階彎曲臨界轉速增加1 372 r/min，但是這是以質量和一階彎曲共振幅值的增加為代價的，其中質量增加1.51 kg,一階彎曲共振最大變形量增加0.024 mm。在實際工程中，可以根據要求進行取舍。

需要說明的是，工程中轉子結構動力學優化設計包含著更多的內容。例如，在航空發動機轉子結構設計中，轉子結構的平衡配重是在有限個轉速下進行的，因此在飛行包線內仍存在一定的不平衡響應，這時為了保證轉子具有足夠的抗變形能力，需要結構對不平衡量的敏感性降到最低，即結構對不平衡量的低敏感性設計。例如，低壓轉子的動撓度曲線形狀和彎曲程度隨轉速而變化，當轉速接近某階臨界轉速時，該階陣型分量最大。如果軸承支點位置布置不合理，距離振型節點較遠，將會大大增加軸承的支反力，轉子系統可靠性急劇降低，這就需要通過調整局部構型以期改變振動振型，從而達到降低軸承支反力的目的。本文所涉及的構型優化僅是為了闡述布局優化設計的實現方法、可行性和重要意義，并不針對具體型號的發動機轉子及其出現的具體問題做分析，所以計算結果可能與實際發動機轉子存在偏差。同時，為了節省篇幅和簡化計算，略去了工程上其他諸多方面的布局優化仿真。

圖9 力學環境適應能力優化響應面Fig.9 Response surface of mechanical environment adaptability optimization

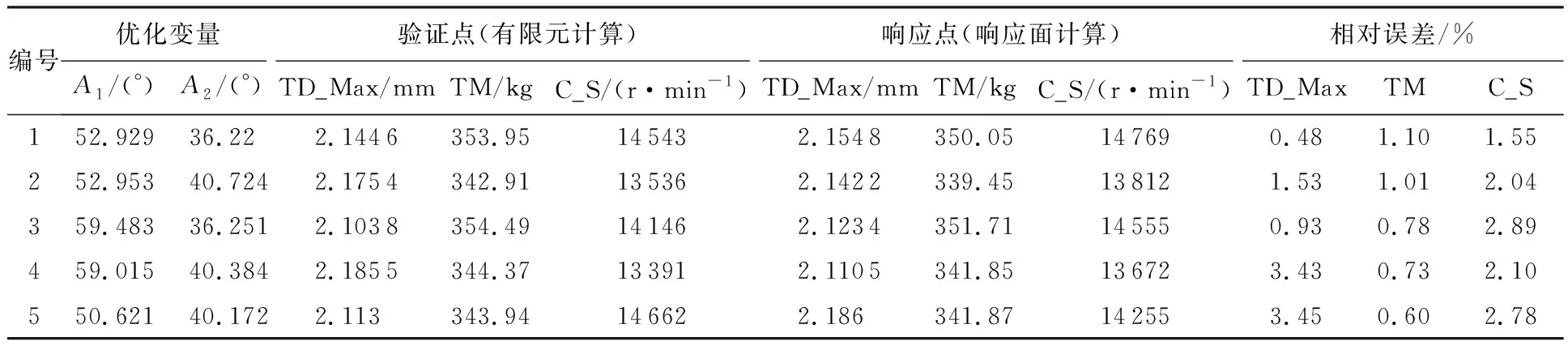
表7 力學環境適應能力響應面誤差驗證Table 7 Error verification of response surface of mechanical environment adaptability

表8 力學環境適應能力優化設計結果Table 8 Design results of mechanical environment adaptability optimization

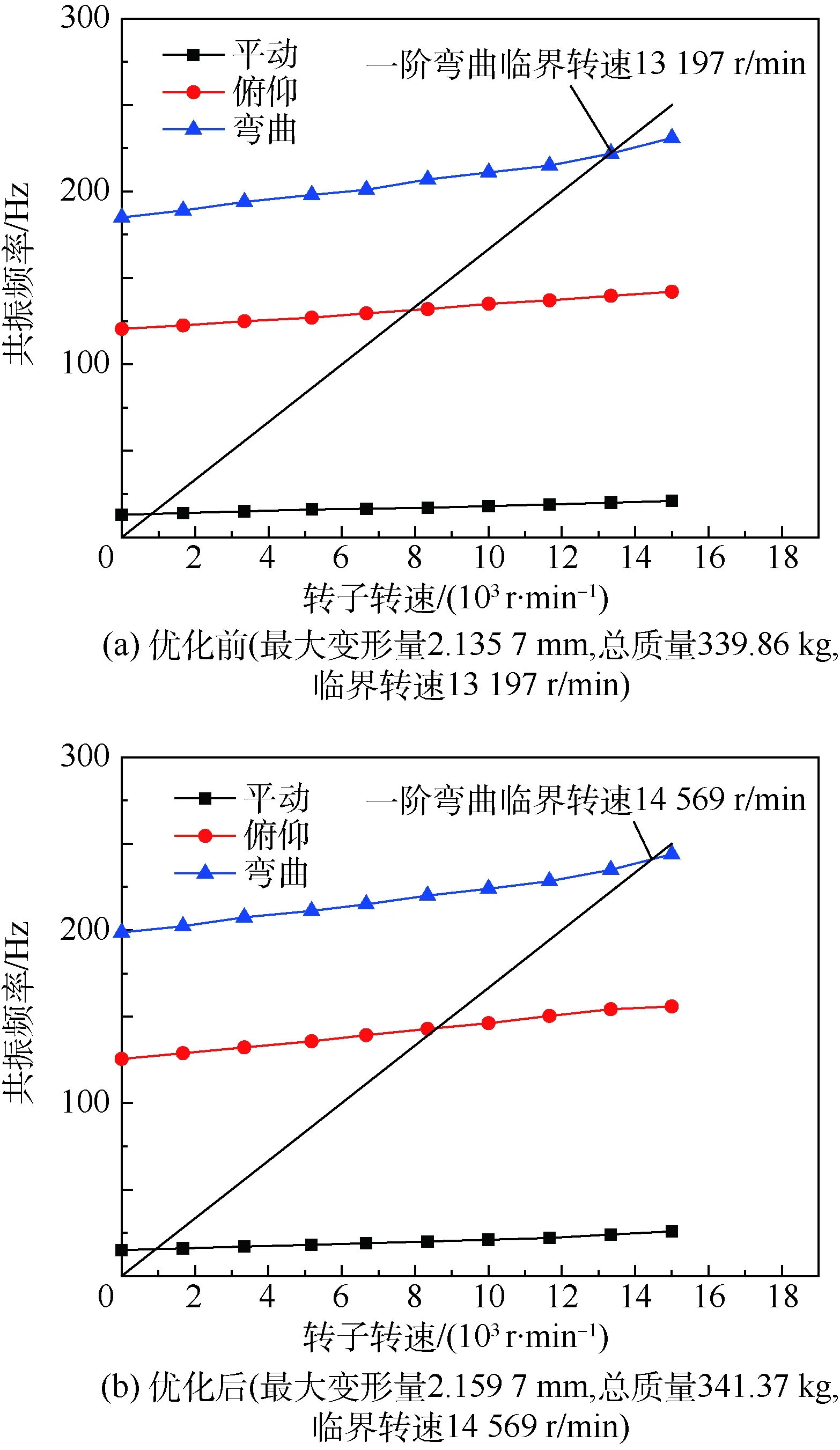
圖10 力學環境適應能力優化前后對比Fig.10 Comparison of results before and after mechanical environment adaptability optimization

5 工程結構綜合優化示例

以兩支點高速轉子結構系統為背景，為了建立具有通用性的優化流程，掌握結構幾何構形和尺寸變化對轉子力學特性的影響規律，本節以轉子結構的結構效率為目標，對其進行多目標綜合優化設計，使本文提出的結構布局設計方法更具工程應用價值。

對高壓轉子初始施加國軍標所要求的橫向過載載荷和機動飛行的角加速度，高壓轉子工作轉速為12 000 r/min，通過有限元法綜合考慮結構的抗變形能力和力學環境適應能力，優化的目標是控制轉子系統結構總質量的前提下，使轉子結構效率損失降到最低。定義結構布局優化的數學表達式如下：

(1)

式(1)即為目標函數。式中：X為關鍵設計參數組成的參數向量；f為環境載荷；w(X，f)為徑向撓曲變形；SP為轉子俯仰振型對應的臨界轉速；SB為一階彎曲對應的臨界轉速；Y為結構力學特征參數；σave(X,f)為外加環境載荷下結構的平均應力系數，表達式如下：

(2)

其中：σi為第i個結構單元的應力；mi為第i個單元的質量。平均應力系數反映了材料的使用效率。

式(1)是一個多參數、多目標的優化問題，也可以在結構效率的意義下，將其合并成一個參數，定義為結構效率損失系數：

(3)

式中：a、b、c、d為加權系數，可根據工程實際進行適當選取。可把結構效率損失系數作為結構合理性的度量。以此為目標函數，首先基于斯珀曼法的參數關聯性分析得到如表9所示的參數關聯性矩陣。可以看出，對結構效率損失系數影響較大的2個構形參數為A1和A2，故選定A1和A2作為關鍵特征參數。

表9 參數關聯性矩陣Table 9 Parameter correlation matrix

基于有限元法，采用稀疏網格響應面對試驗點數據擬合，得到如圖11所示的響應面，圖中S_E為結構效率損失系數。基于多目標遺傳算法，通過響應面可以較為容易地找到極小值點(A1,A2)=(49.6°,37.5°)，該點即是優化后的最優構形點。優化前后的總變形如圖12所示。

按照式(3)定義的結構效率損失系數為目標函數，優化后的結構效率損失系數(0.646)同優化前(0.981)相比，下降0.335，使結構總質量基本不變的條件下，轉子剛度特性大幅提高。從參數關聯性矩陣也可以看出，中間軸段傾角(A2)對轉子剛度特性產生較大影響，合理的傾角選取可以有效提升結構的抗變形能力。從總體變形云圖(見圖12)上也可以看出，不僅結構效率損失系數有所下降，而且整體變形的分布形式并沒有較大變化，這對結構整體性能提升是有意義的。

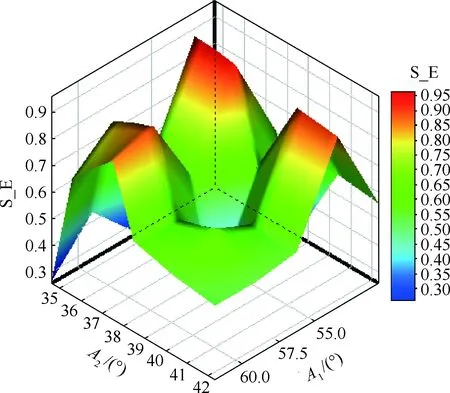
圖11 擬合響應面Fig.11 Fitting response surface

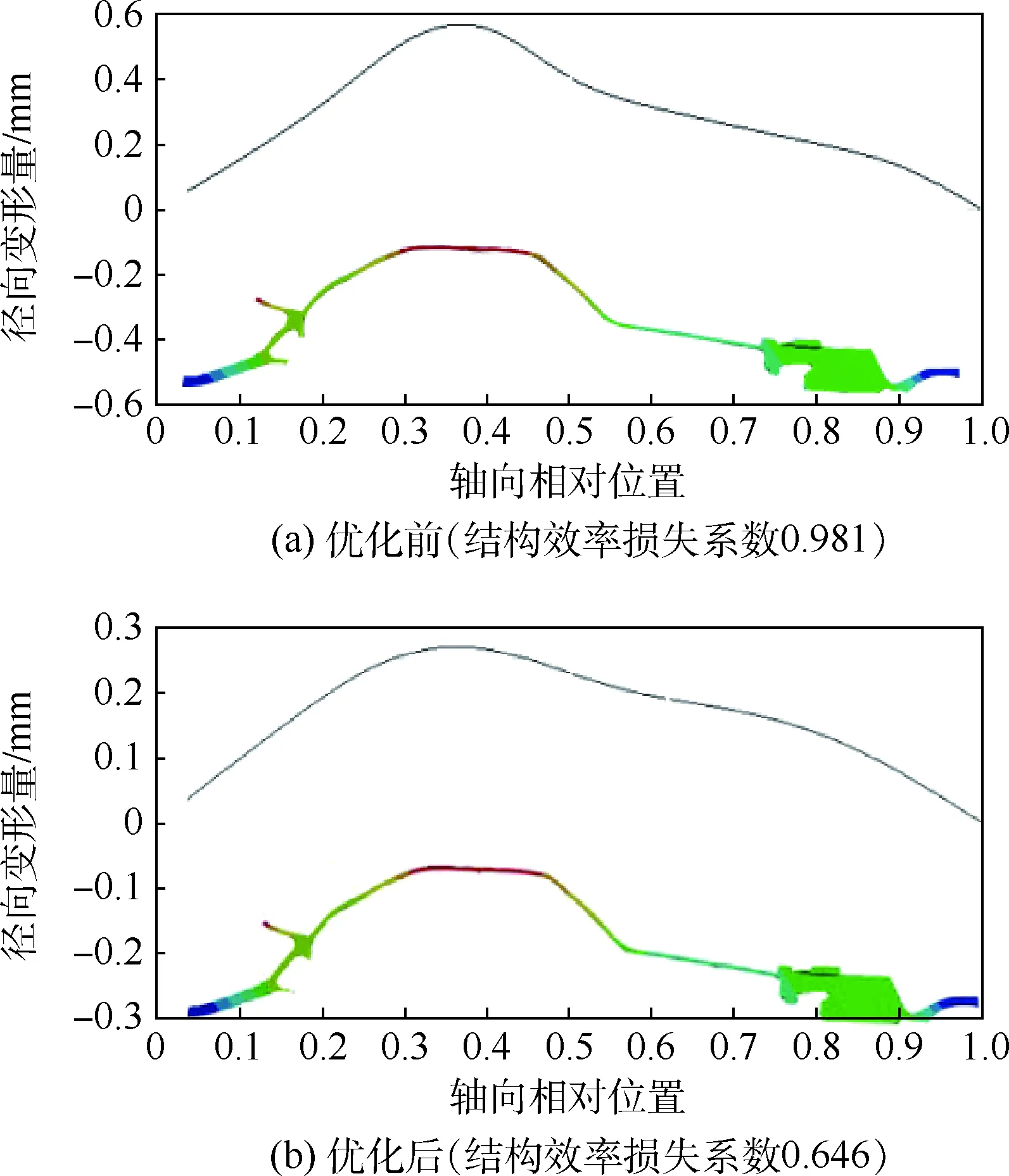
圖12 優化前后結構總體變形Fig.12 Overall structure deformation before and after optimization

6 結 論

本文提出的航空發動機轉子結構布局設計方法是為適應新一代先進航空發動機轉子結構研制順勢而出，是擺脫過多依靠傳統設計經驗，實現其先進性的有效途徑，該方法不僅適合渦扇發動機，對渦軸、渦槳等同樣適用。同時，轉子結構布局設計方法補充了原轉子結構效率的內容，在對轉子結構力學特征定量評估的基礎上，提供了最優或次優的結構布局易行方法。

1) 航空發動機轉子構型的合理設計，特別是中間軸段的合理設計，可以有效提升轉子的抗變形能力和力學環境適應能力。算例結果表明，通過對結構構型的布局優化設計，與原始結構相比，抗變形能力優化設計使高壓轉子整體提升了近28%的慣性剛度，力學環境適應能力優化設計使轉子系統的一階彎曲臨界轉速提高1 372 r/min，同時給出了多目標綜合優化設計方法，最大程度降低了結構效率損失系數。通過對轉子結構布局優化設計，完全可以達到將不合理的結構構型最大程度合理化的效果，這對航空發動機轉子系統結構改進設計，乃至整機結構布局優化設計具有著重要的借鑒意義。

2) 在航空發動機轉子結構布局優化設計時，除了要考慮優化目標達到技術要求外，同時需要兼顧其他力學特征是否發生嚴重改變，是否依然符合技術要求。例如，本文在力學環境適應能力優化時，雖然一階彎曲臨界轉速實現了1 372 r/min的增加，但是結構總質量也和一階彎曲時的最大變形量均有少許增加。

本文僅以航空發動機高壓轉子構型為例，探索其結構關鍵特征參數，并對轉子結構抗變形能力和力學環境適應能力進行了布局優化設計。實際工程中，可能需要考慮更多的實際環境因素，如在高溫、高壓、流固耦合等復雜環境下對航空發動機雙轉子系統和整機的結構布局優化設計，這仍有待進一步的研究。