觸地關(guān)機(jī)模式下的著陸器軟著陸穩(wěn)定性研究

董洋， 王春潔,2,*， 吳宏宇， 丁宗茂， 滿劍鋒

(1. 北京航空航天大學(xué) 機(jī)械工程及自動(dòng)化學(xué)院, 北京 100083；2. 北京航空航天大學(xué) 虛擬現(xiàn)實(shí)技術(shù)與系統(tǒng)國家重點(diǎn)實(shí)驗(yàn)室, 北京 100083)

腿式著陸器因其結(jié)構(gòu)簡單、可靠性較高等特點(diǎn)，在各國地外星球探測任務(wù)中普遍被選擇。目前，腿式著陸器性能的研究和驗(yàn)證方法主要有物理樣機(jī)實(shí)驗(yàn)和虛擬樣機(jī)仿真。前者由于成本較高，且其他星球的重力環(huán)境在實(shí)驗(yàn)過程中很難模擬，故難以研究著陸器在多種工況下的性能。隨著計(jì)算機(jī)運(yùn)算能力的快速增長，后者的高效率和低成本等優(yōu)點(diǎn)不斷凸顯，逐漸成為著陸器研制過程中不可或缺的環(huán)節(jié)。

文獻(xiàn)[1-3]提出了地球重力下的著陸沖擊實(shí)驗(yàn)方法，研究了腿式著陸器在典型工況下的軟著陸性能。文獻(xiàn)[4-7]建立了著陸器的動(dòng)力學(xué)仿真模型，研究了典型工況下的著陸器軟著陸性能，其中文獻(xiàn)[6]通過對(duì)比仿真與實(shí)驗(yàn)結(jié)果，證明了建模的準(zhǔn)確性。文獻(xiàn)[8-9]基于理論分析給出著陸參數(shù)穩(wěn)定性邊界，其中文獻(xiàn)[9]通過實(shí)驗(yàn)對(duì)邊界進(jìn)行驗(yàn)證。文獻(xiàn)[10-11]基于腿式著陸器非0高度關(guān)機(jī)軟著陸模式下的動(dòng)力學(xué)仿真模型，結(jié)合離散化搜尋的仿真策略，給出了主要工況參數(shù)的二維穩(wěn)定性邊界，其中文獻(xiàn)[11]在給出穩(wěn)定性邊界的過程中引入了響應(yīng)面方法，提高了計(jì)算效率。文獻(xiàn)[12-14]在腿式著陸器的動(dòng)力學(xué)仿真模型中添加了主發(fā)動(dòng)機(jī)與姿態(tài)控制發(fā)動(dòng)機(jī)的推力等效模型，研究了著陸器的觸地關(guān)機(jī)軟著陸穩(wěn)定性，但未給出直觀的穩(wěn)定性邊界。

有鑒于此，本文以某型著陸器為研究對(duì)象，利用ADAMS軟件建立其觸地關(guān)機(jī)軟著陸模式下的動(dòng)力學(xué)仿真模型，結(jié)合仿真模型與優(yōu)化方法確定了多組極惡劣地形工況，并結(jié)合徑向基函數(shù)(RBF)神經(jīng)網(wǎng)絡(luò)代理模型，給出了速度的三維穩(wěn)定性邊界。

1 著陸器動(dòng)力學(xué)建模

1.1 著陸器整機(jī)模型

本文研究的某型著陸器裝有4套中心對(duì)稱分布于主體的緩沖機(jī)構(gòu)，如圖1所示，著陸器是由多個(gè)構(gòu)件通過運(yùn)動(dòng)副連接且受到復(fù)雜的外力作用的多體系統(tǒng)，分析著陸器軟著陸性能，需基于多體動(dòng)力學(xué)理論，建立著陸器的多體動(dòng)力學(xué)模型。其基本動(dòng)力學(xué)方程如下[15]:

(1)

(2)

(3)

式中：M為廣義質(zhì)量矩陣，由著陸器各構(gòu)件質(zhì)量和轉(zhuǎn)動(dòng)慣量構(gòu)成；Ф為運(yùn)動(dòng)副約束方程矢量；q為廣義坐標(biāo)矢量；Фq為約束方程的雅克比矩陣；Q為廣義力，主要考慮發(fā)動(dòng)機(jī)推力和接觸力；λ為拉格朗日乘子矢量；t為時(shí)間。結(jié)合所建立的著陸器的動(dòng)力學(xué)模型，利用ADAMS軟件進(jìn)行仿真分析。

緩沖機(jī)構(gòu)主要由主支柱、緩沖桿、左右輔助支柱和足墊組成[12-14]。緩沖桿在受到?jīng)_擊時(shí)會(huì)發(fā)生塑性變形，其建模方法參考文獻(xiàn)[12]的剛體等效法。如圖2所示，αe、Me和Se分別為緩沖桿的等效轉(zhuǎn)角、等效彎矩和等效軸向位移，先在有限元軟件中建立緩沖桿的模型，進(jìn)行仿真分析，可以得到圖3所示的αe-Me和αe-Se曲線，然后將曲線導(dǎo)入剛體模型之中即可完成緩沖桿的等效建模。

輔助支柱內(nèi)外筒之間的緩沖元件力學(xué)特性通過有限元分析獲得，進(jìn)而確定輔助支柱的壓縮位移DS和緩沖力FS之間關(guān)系如圖4所示。將DS-FS曲線導(dǎo)入剛體模型之中完成其等效建模。

足墊和著陸面的接觸采用庫倫摩擦模型模擬切向力，采用非線性彈簧阻尼模型模擬法向碰撞力[12]。

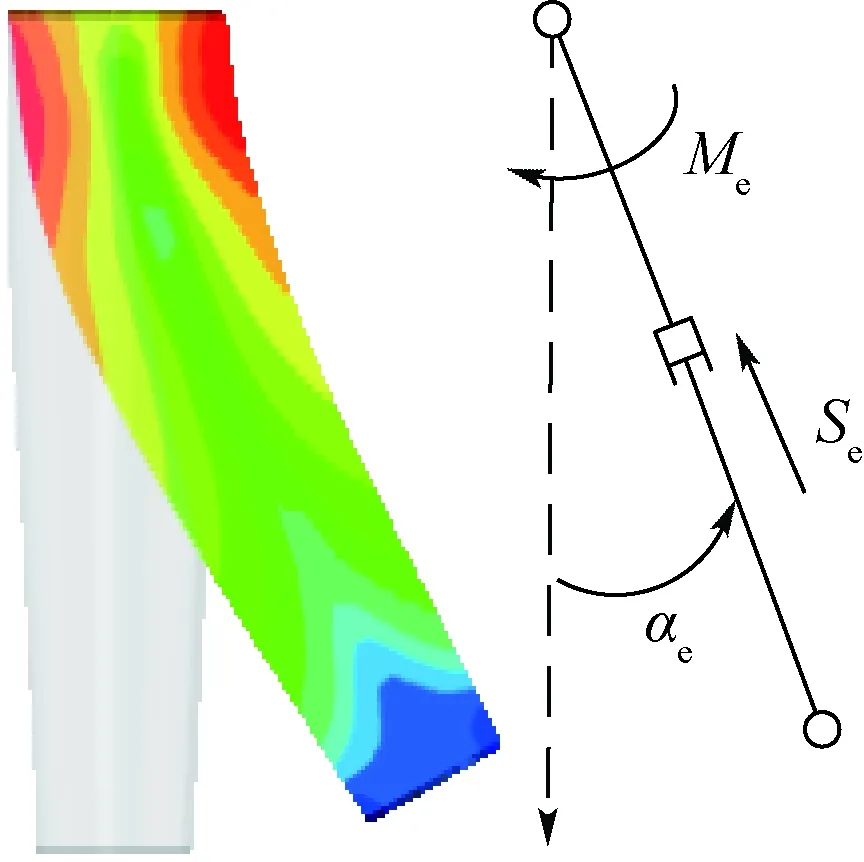
圖2 緩沖桿等效模型Fig.2 Equivalent model of buffer rod

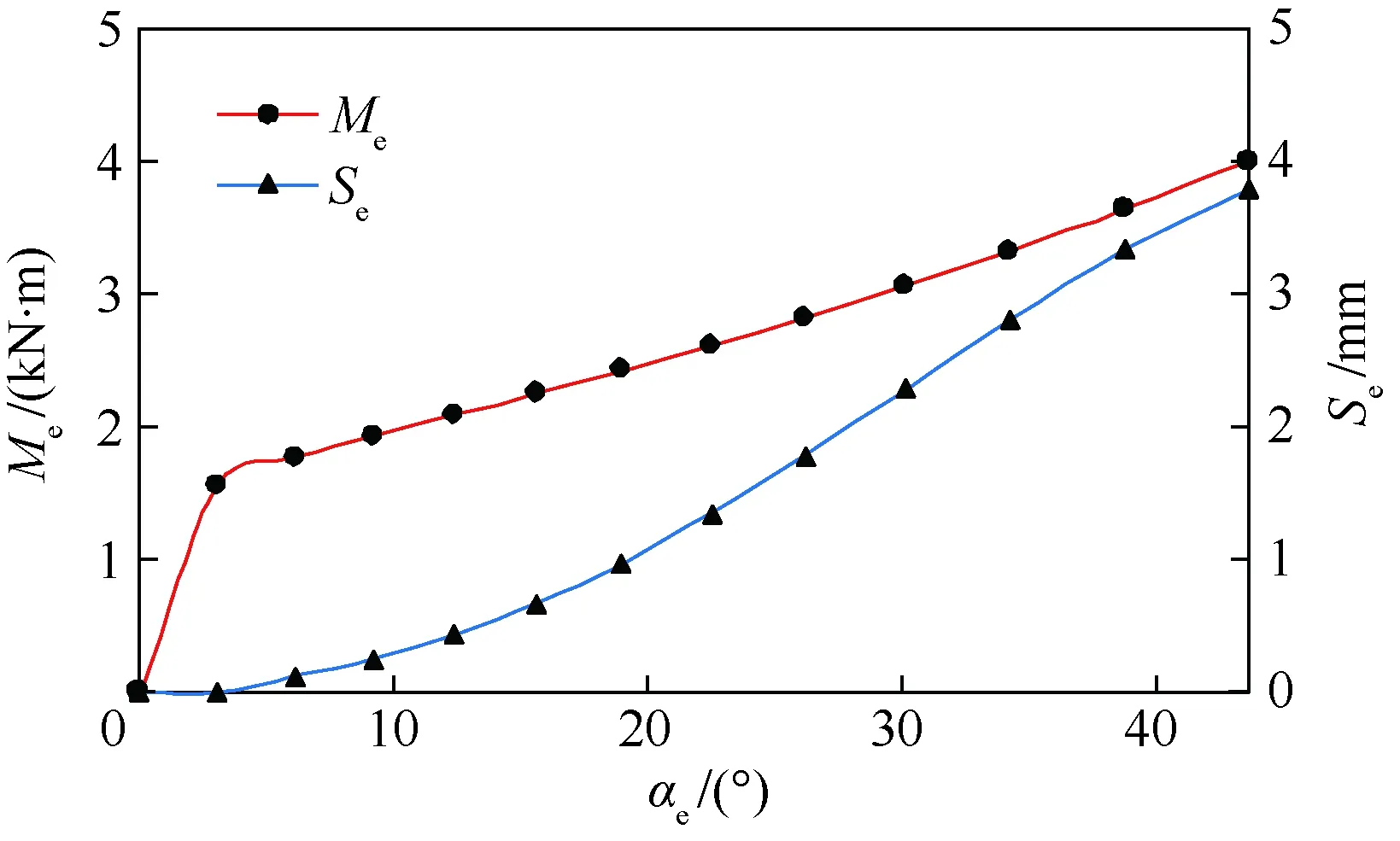
圖3 緩沖桿力學(xué)特性Fig.3 Mechanical behavior of buffer rod

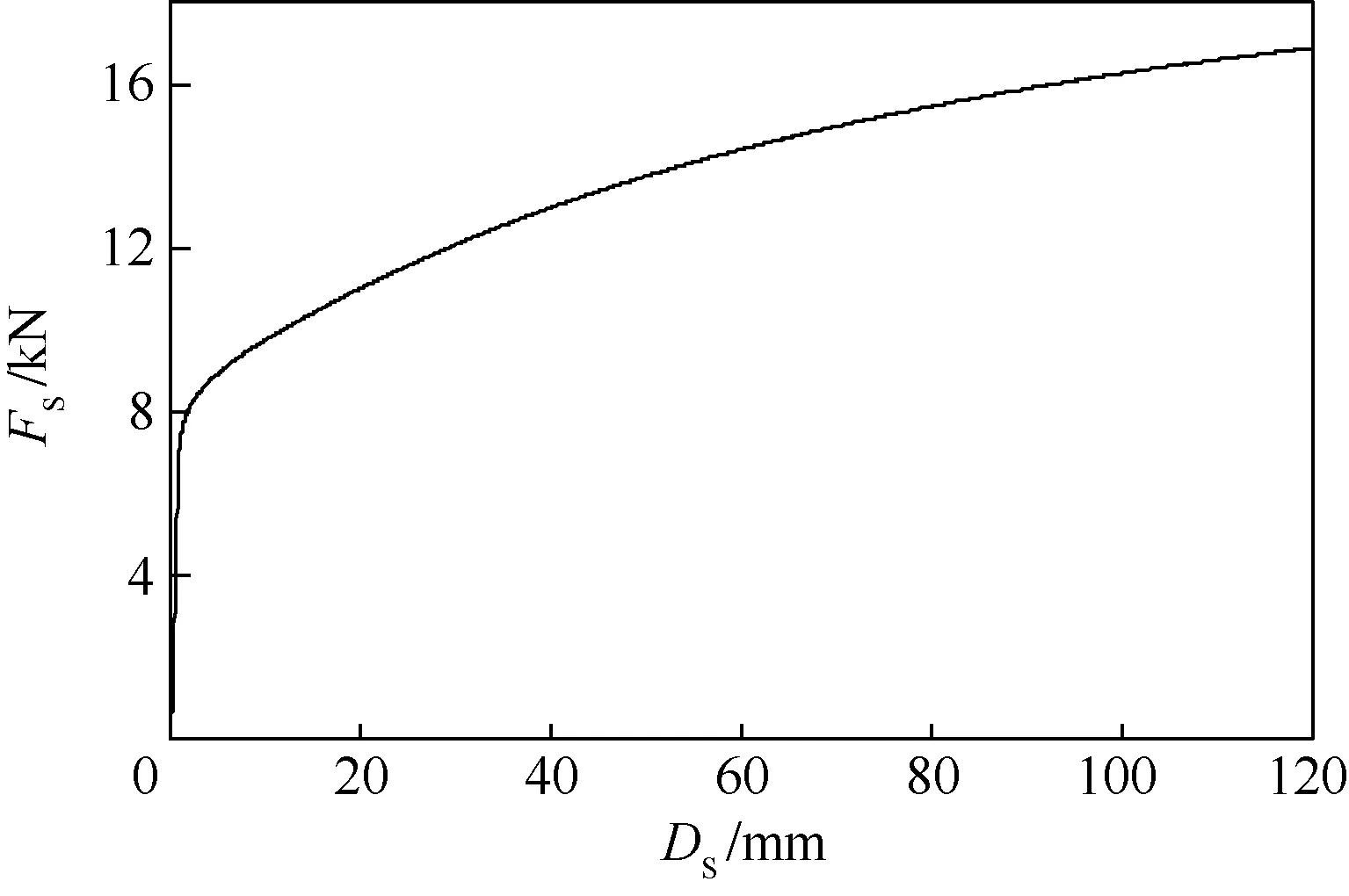
圖4 緩沖元件力學(xué)特性Fig.4 Mechanical behavior of cushion element

1.2 發(fā)動(dòng)機(jī)動(dòng)力系統(tǒng)等效建模

著陸器主體上裝有一個(gè)用于制動(dòng)的主發(fā)動(dòng)機(jī)和多臺(tái)用于姿態(tài)調(diào)節(jié)的姿控發(fā)動(dòng)機(jī)。觸地關(guān)機(jī)軟著陸模式下，發(fā)動(dòng)機(jī)作用對(duì)著陸器的軟著陸穩(wěn)定性不能忽視，因此需要建立考慮發(fā)動(dòng)機(jī)作用效果的著陸器動(dòng)力學(xué)仿真模型。

1.2.1 姿控發(fā)動(dòng)機(jī)控制策略

除主發(fā)動(dòng)機(jī)外，觸地關(guān)機(jī)軟著陸模式下還有10臺(tái)姿控發(fā)動(dòng)機(jī)處于開啟狀態(tài)，各發(fā)動(dòng)機(jī)的位置如圖5所示。其中，2臺(tái)位于主體上方，編號(hào)A1、A2，8臺(tái)位于著陸器主體下方，編號(hào)B1～B8。

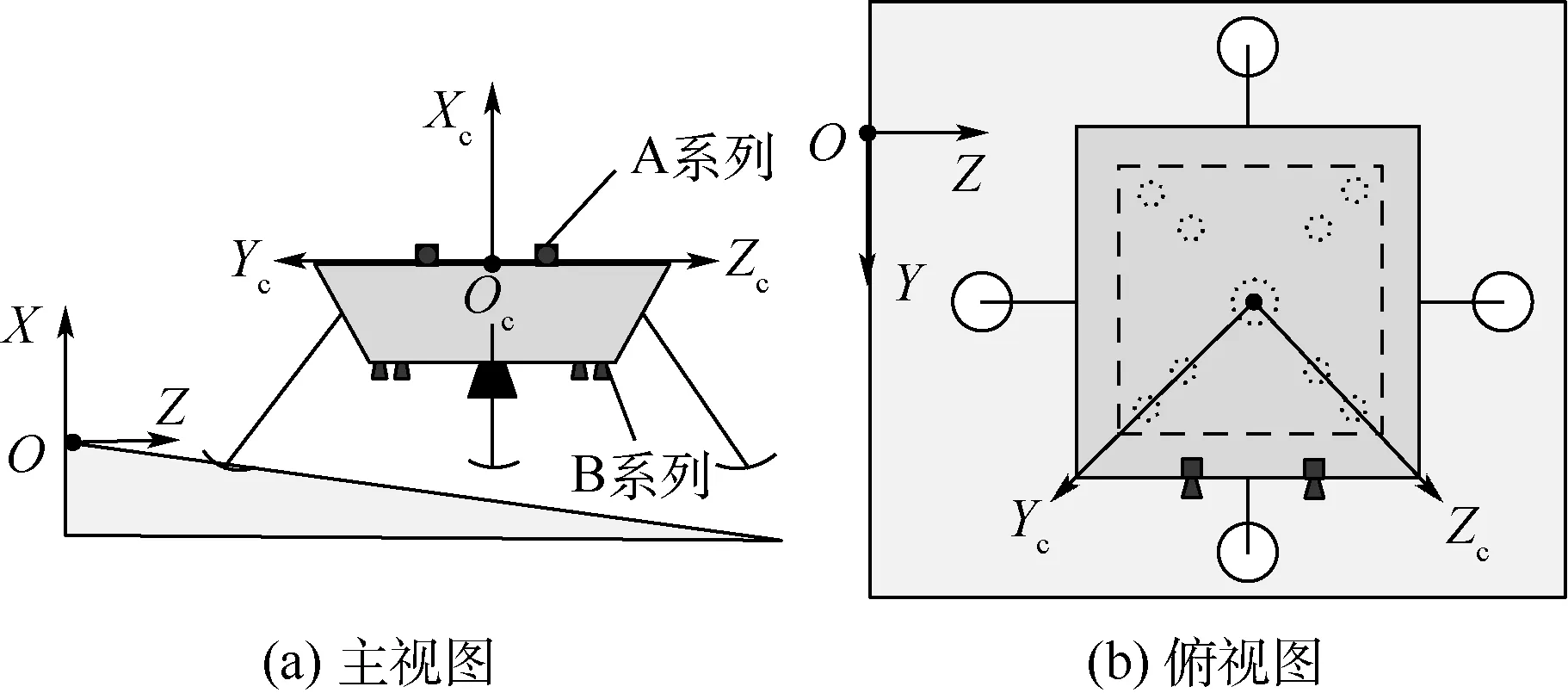
圖5 坐標(biāo)系定義及發(fā)動(dòng)機(jī)位置Fig.5 Coordinate system definition and engine position

此外，圖5還包括了與姿態(tài)控制相關(guān)的坐標(biāo)系。其中，O-XYZ為地面固定坐標(biāo)系(右手系)，X軸沿重力方向指向天空，Z軸水平指向下坡方向。Oc-XcYcZc為隨體控制坐標(biāo)系(右手系)，原點(diǎn)在著陸平臺(tái)中心，Xc軸垂直著陸平臺(tái)表面且指向天空，Zc軸在著陸平臺(tái)內(nèi)且在俯視圖中指向相鄰兩足墊的中點(diǎn)。定義O-XYZ按照Z-Y-X的順序旋轉(zhuǎn)到與Oc-XcYcZc平行位置時(shí)繞三軸轉(zhuǎn)動(dòng)的角度分別為θx、θy、θz；同時(shí)定義Oc-XcYcZc相對(duì)O-XYZ的角速度矢量在Oc-XcYcZc三軸上的投影分別為ωx、ωy、ωz。將上述6個(gè)參數(shù)作為控制輸入。

為提升著陸器姿態(tài)的穩(wěn)定性，A1、A2發(fā)動(dòng)機(jī)的推力如式(4)和式(5)所示；B系列發(fā)動(dòng)機(jī)的推力公式形式相同，均參考文獻(xiàn)[12]建立，以B1、B2為例，其推力如式(6)所示：

FA1=

(4)

FA2=

(5)

FBi=

i=1,2

(6)

式中：ai、bi、ki為控制策略中的相關(guān)參數(shù)；FM1與FM2分別為2 個(gè)系列發(fā)動(dòng)機(jī)推力最大值。

1.2.2 主發(fā)動(dòng)機(jī)控制策略

主發(fā)動(dòng)機(jī)位于主體下表面中心且噴口方向垂直主體下表面。正常工作時(shí)，其推力方程為[12]

(7)

式中：m為著陸器整機(jī)質(zhì)量；vx為豎直速度值。

觸地關(guān)機(jī)軟著陸模式下，若足墊與星球表面接觸，則其內(nèi)部的傳感器將發(fā)出主發(fā)動(dòng)機(jī)關(guān)機(jī)信號(hào)，但主發(fā)動(dòng)機(jī)由于關(guān)機(jī)后效其推力不能馬上減小到零，該情況會(huì)對(duì)著陸穩(wěn)定性產(chǎn)生影響[16]，因此，為了提高著陸穩(wěn)定性，姿控發(fā)動(dòng)機(jī)會(huì)在主發(fā)動(dòng)機(jī)收到關(guān)機(jī)指令之后延遲關(guān)機(jī)。關(guān)機(jī)信號(hào)發(fā)出后，由于信號(hào)傳輸?shù)难舆t，主發(fā)動(dòng)機(jī)推力下降開始時(shí)間會(huì)滯后。其推力變化過程如圖6所示。圖中：t0為觸地時(shí)刻，t1時(shí)刻發(fā)出關(guān)機(jī)信號(hào)，t2時(shí)刻推力開始下降，t3時(shí)刻姿控發(fā)動(dòng)機(jī)關(guān)閉。

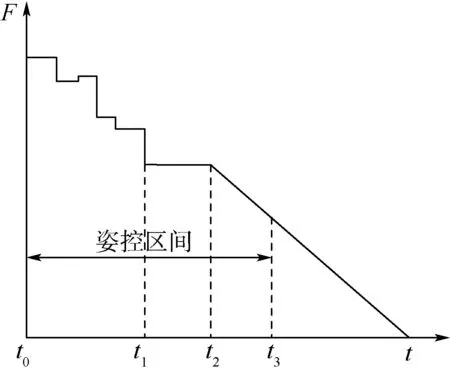
圖6 主發(fā)動(dòng)機(jī)推力變化過程Fig.6 Thrust changing process of main engine

1.2.3 發(fā)動(dòng)機(jī)推力等效建模

本文通過在發(fā)動(dòng)機(jī)安裝位置添加與發(fā)動(dòng)機(jī)噴口方向相反的力來模擬發(fā)動(dòng)機(jī)的推力作用效果，并利用測量函數(shù)實(shí)時(shí)反饋θx、θy、θz、ωx、ωy、ωz與vx的值。在真實(shí)情況下，由于傳感器按給定周期采集和處理信號(hào)，故推力值不隨位姿和速度參數(shù)連續(xù)變化[17]，因此，本文在根據(jù)式(7)計(jì)算推力值的同時(shí)，也按照給定周期給模型中的推力賦值，以模擬發(fā)動(dòng)機(jī)的真實(shí)工作情況。

2 著陸工況參數(shù)與軟著陸穩(wěn)定性判據(jù)

2.1 著陸工況參數(shù)

本文考慮的著陸工況參數(shù)有2類：

1) 地形參數(shù)。包括著陸面坡度(α)、足墊滑移狀態(tài)(K)和著陸偏航角(ψ)。由于著陸器安裝有地貌識(shí)別系統(tǒng)，正常情況下會(huì)降落在平原地區(qū)，坡度一般不超過12°，本文考慮著陸面坡度為0°～12°。正常情況下足墊可以在著陸面上滑移，但如果足墊遇到石塊或者小坑，其將處于卡死狀態(tài)，本文用K=0表示足墊可滑移，K=1表示足墊卡死。考慮著陸器的幾何對(duì)稱性，ψ取0°～45°即可以表征所有用于評(píng)判著陸器軟著陸穩(wěn)定性的姿態(tài)。

2) 著陸速度。指著陸器相對(duì)地面固定坐標(biāo)系的速度，為空間矢量。為方便后文的研究，著陸速度采用柱坐標(biāo)系(vh，β，vx)描述，vh(0～2.5 m/s)為速度在ZOY平面投影的模長，即水平速度大小；β(0°～360°)為從+X方向看，Z軸繞到水平速度方向轉(zhuǎn)過的角度；vx為豎直速度大小(0～5 m/s)，其方向沿-X方向。

部分著陸工況參數(shù)如圖7所示。

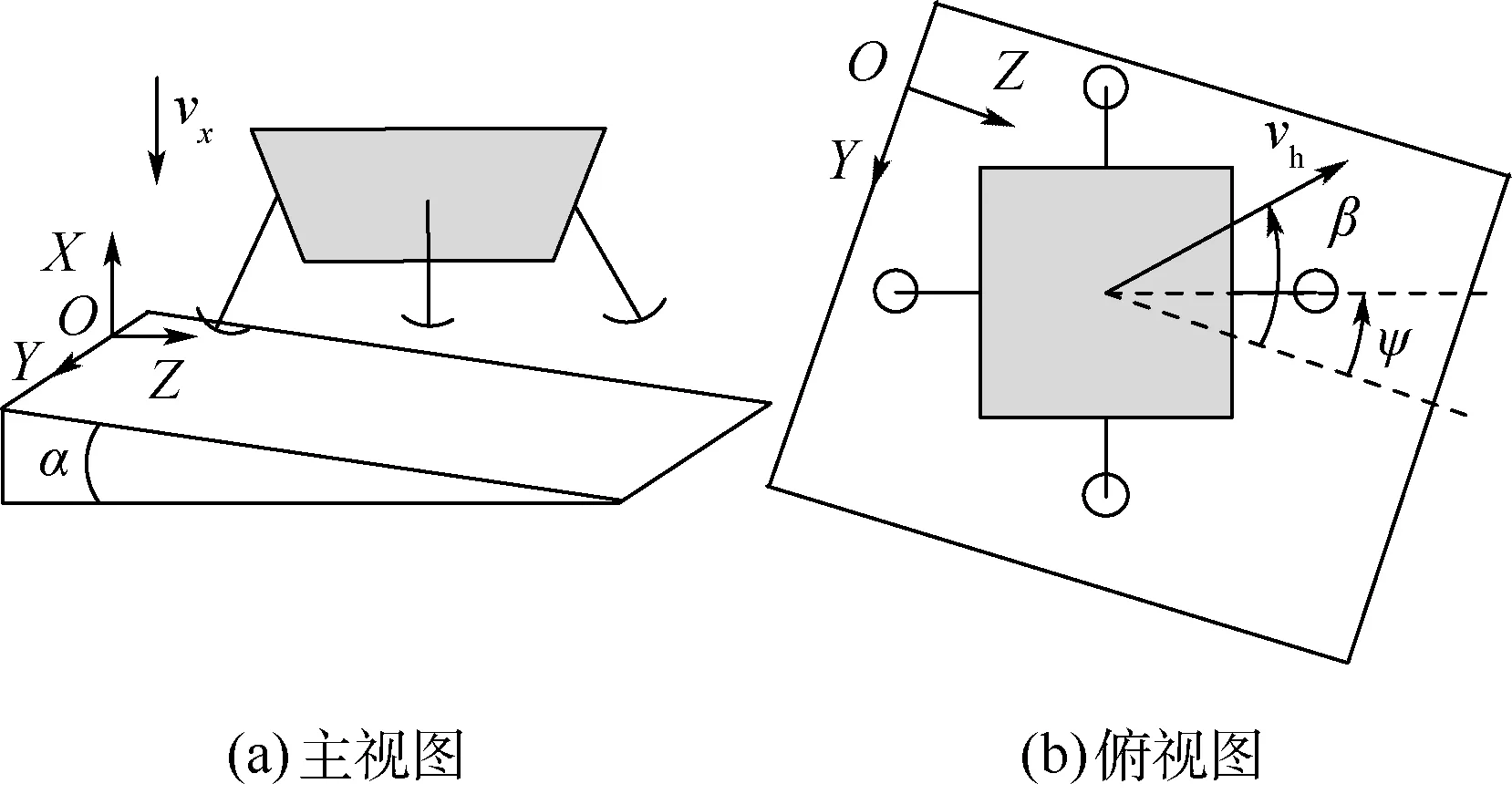
圖7 部分著陸工況參數(shù)示意圖Fig.7 Schematic diagram of partial landing conditions parameters

2.2 軟著陸穩(wěn)定性判據(jù)

本文重點(diǎn)研究著陸器的軟著陸穩(wěn)定性，根據(jù)著陸器構(gòu)型，確定其穩(wěn)定性評(píng)判參數(shù)如下：

1) 緩沖桿最大等效轉(zhuǎn)角αem(單位為(°))。緩沖桿通過塑性變形吸收沖擊能量，若等效轉(zhuǎn)角過大其極易發(fā)生損壞，故αem應(yīng)小于許用值α*。

2) 輔助支柱最大壓縮行程DSM(單位為mm)。一方面應(yīng)避免DSM超過設(shè)計(jì)壓縮范圍，另一方面，DSM過大易導(dǎo)致著陸平臺(tái)和坡面夾角過大，不利于探測車的轉(zhuǎn)移，故DSM應(yīng)小于許用值D*。

3) 著陸器質(zhì)心到4個(gè)翻倒平面距離的最小值LD(單位為mm)。定義通過相鄰兩個(gè)足墊中心的豎直平面為翻倒平面[11]，為保證著陸器在軟著陸過程中不發(fā)生翻倒，LD應(yīng)大于許用值L*。

4) 主發(fā)動(dòng)機(jī)尾噴管底面中心到著陸面的最小距離HM(單位為mm)。觸地關(guān)機(jī)軟著陸過程中，主發(fā)動(dòng)機(jī)大部分時(shí)間處于開啟狀態(tài)，考慮HM過小容易導(dǎo)致粉塵堵塞尾噴管或凸起撞擊尾噴管等情況，故HM應(yīng)大于許用值H*。

3 極惡劣地形的確定

著陸工況參數(shù)中，α、K、ψ依賴于星球的地形，難以主動(dòng)預(yù)測或者控制，而vx、vh、β作為著陸器自身的參數(shù)，具有一定的可控性，為了研究可控參數(shù)對(duì)著陸器軟著陸穩(wěn)定性的具體影響方式，有必要事先確定α、K、ψ的最壞取值。基于動(dòng)力學(xué)模型，本文采用優(yōu)化方法尋找考慮著陸器水平速度、使穩(wěn)定性指標(biāo)αem、DSM、LD、HM最差的α、K、ψ取值。為了降低優(yōu)化維度、提高計(jì)算效率，設(shè)定vx=2.5 m/s、vh=1.0 m/s，考慮水平速度大小固定的情況下，β取值的不同可能帶來α、K、ψ最差取值的不同，故將β作為尋找最差工況的變量之一。綜上，以尋找LD最差的工況為例，建立優(yōu)化模型如下：

minLD(X)X=[α,K,ψ,β]T∈Ω

(8)

式中：Ω為參數(shù)的取值范圍。

本文使用多島遺傳算法(MIGA)、結(jié)合動(dòng)力學(xué)模型實(shí)現(xiàn)優(yōu)化計(jì)算，算法參數(shù)配置如表1所示。

經(jīng)優(yōu)化計(jì)算，得到4組極惡劣工況如表2所示。

表1 優(yōu)化參數(shù)設(shè)置Table 1 Setting of optimal parameters

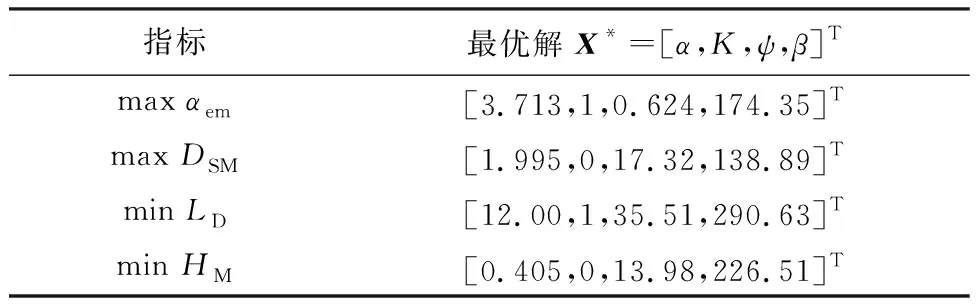
表2 極惡劣工況Table 2 Worst landing conditions

4 可控工況參數(shù)分析

4.1 單穩(wěn)定性指標(biāo)的速度穩(wěn)定性邊界

研究vx、vh、β對(duì)著陸器軟著陸穩(wěn)定性的具體影響方式的過程中，需進(jìn)行大規(guī)模仿真計(jì)算，為了提高效率，本文引入RBF神經(jīng)網(wǎng)絡(luò)代理模型建立極惡劣工況下的vx、vh、β與4項(xiàng)軟著陸穩(wěn)定性指標(biāo)值之間的映射關(guān)系[18]。通過隨機(jī)抽點(diǎn)仿真，將仿真結(jié)果導(dǎo)入神經(jīng)網(wǎng)絡(luò)模型進(jìn)行訓(xùn)練，用400個(gè)獨(dú)立的樣本測試模型，訓(xùn)練終止準(zhǔn)則為均方根相對(duì)誤差值RMSE(見式(9))小于0.05。

(9)

得到神經(jīng)網(wǎng)絡(luò)模型后，本文采用控制變量法，令vx、vh、β在取值范圍內(nèi)等間距抽取100個(gè)點(diǎn)，共得到106組樣本點(diǎn)，將其代入神經(jīng)網(wǎng)絡(luò)模型中，計(jì)算得到106組軟著陸穩(wěn)定性指標(biāo)值。綜合考慮著陸器的軟著陸可靠性與模型誤差等因素，設(shè)定本文的各項(xiàng)軟著陸穩(wěn)定性指標(biāo)許用值分別為α*=30°、D*=70 mm、L*=50 mm、H*=250 mm，進(jìn)而給出了不同vx取值下反映vh、β與αem、DSM、LD、HM關(guān)系的云圖如圖8所示，vh單位為m/s。

此外，本文還在柱坐標(biāo)系下給出了vx、vh、β三維穩(wěn)定性邊界(許用值等值面)，如圖9所示。

1) 緩沖桿最大等效轉(zhuǎn)角分析定性指標(biāo)的速度三維穩(wěn)定性邊界如圖9(a)所示，圖中曲面為αem=30°的等值面。

由圖8(a)可知，在相同vx與vh下，β對(duì)αem影響非常顯著，β越接近180°、αem越大。因此，圖8(a)所示的αem許用值等值線接近直線，并且集中在120°<β<240°范圍內(nèi)，即偏坡上方向；另外隨著vx增大，不穩(wěn)定區(qū)域面積增大。以αem為穩(wěn)

2) 輔助支柱最大壓縮行程分析

由圖8(b)可知，在相同vx下，DSM的許用值等值線接近環(huán)形，可知β對(duì)DSM影響比較小，DSM的主要影響因素為vh。此外，隨著vx增大，不穩(wěn)定區(qū)域面積增大。以DSM為穩(wěn)定性指標(biāo)的速度三維穩(wěn)定性邊界如圖9(b)所示，圖中曲面為DSM=70mm的等值面。

3) 質(zhì)心距翻倒平面最小距離分析

由圖8(c)可知，LD的許用值等值線集中在270°<β <360°方向，即偏坡下方向，表明水平速度方向接近坡下方向時(shí)著陸器更容易翻倒。以LD為穩(wěn)定性指標(biāo)的速度三維穩(wěn)定性邊界如圖9(c)所示，圖中曲面為LD=50mm的等值面。

4) 尾噴管底面中心到著陸面最小距離分析

由圖8(d)可知，在相同vx下，HM的許用值等值線非常光滑且接近圓，說明β對(duì)HM基本沒有影響；以HM為穩(wěn)定性指標(biāo)的速度三維穩(wěn)定性邊界如圖9(d)所示，圖中曲面為HM=250mm的等值面，圖9(d)直觀顯示邊界集中在vx=4～5m/s區(qū)間，一方面表明該指標(biāo)主要受vx影響，同時(shí)vx小于4m/s時(shí)，HM不會(huì)超過安全閾值。

4.2 綜合多項(xiàng)穩(wěn)定性指標(biāo)的速度穩(wěn)定性邊界

將圖9所示的全部三維穩(wěn)定性邊界向同一柱坐標(biāo)系內(nèi)整合，得到圖10所示的綜合三維穩(wěn)定性邊界，同時(shí)得到不同豎直速度下的切面圖如圖11所示，圖中穩(wěn)定區(qū)域?yàn)楦鞣€(wěn)定區(qū)域的交集,vh單位為m/s。

將圖10所示的三維穩(wěn)定性邊界向同一豎直面內(nèi)做旋轉(zhuǎn)投影，得到消除β影響的4項(xiàng)軟著陸穩(wěn)定性指標(biāo)的保守速度穩(wěn)定性邊界，綜合4條保守邊界，可最終確定綜合多項(xiàng)穩(wěn)定性指標(biāo)的速度穩(wěn)定性邊界，如圖12所示。由圖12可以直觀地確定保證著陸器絕對(duì)穩(wěn)定著陸的速度取值范圍。

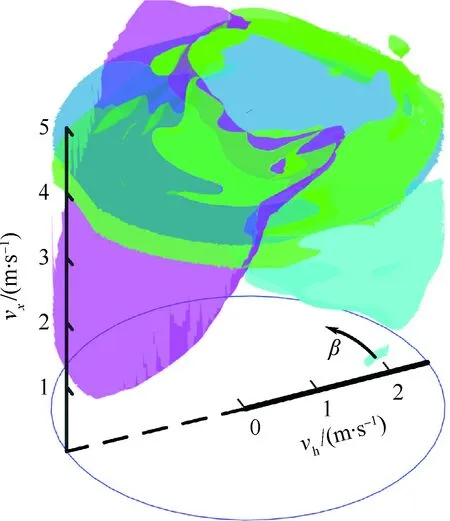
圖10 綜合指標(biāo)下著陸速度三維穩(wěn)定性邊界Fig.10 3D stability boundary determined by landing velocity considering comprehensive indicators

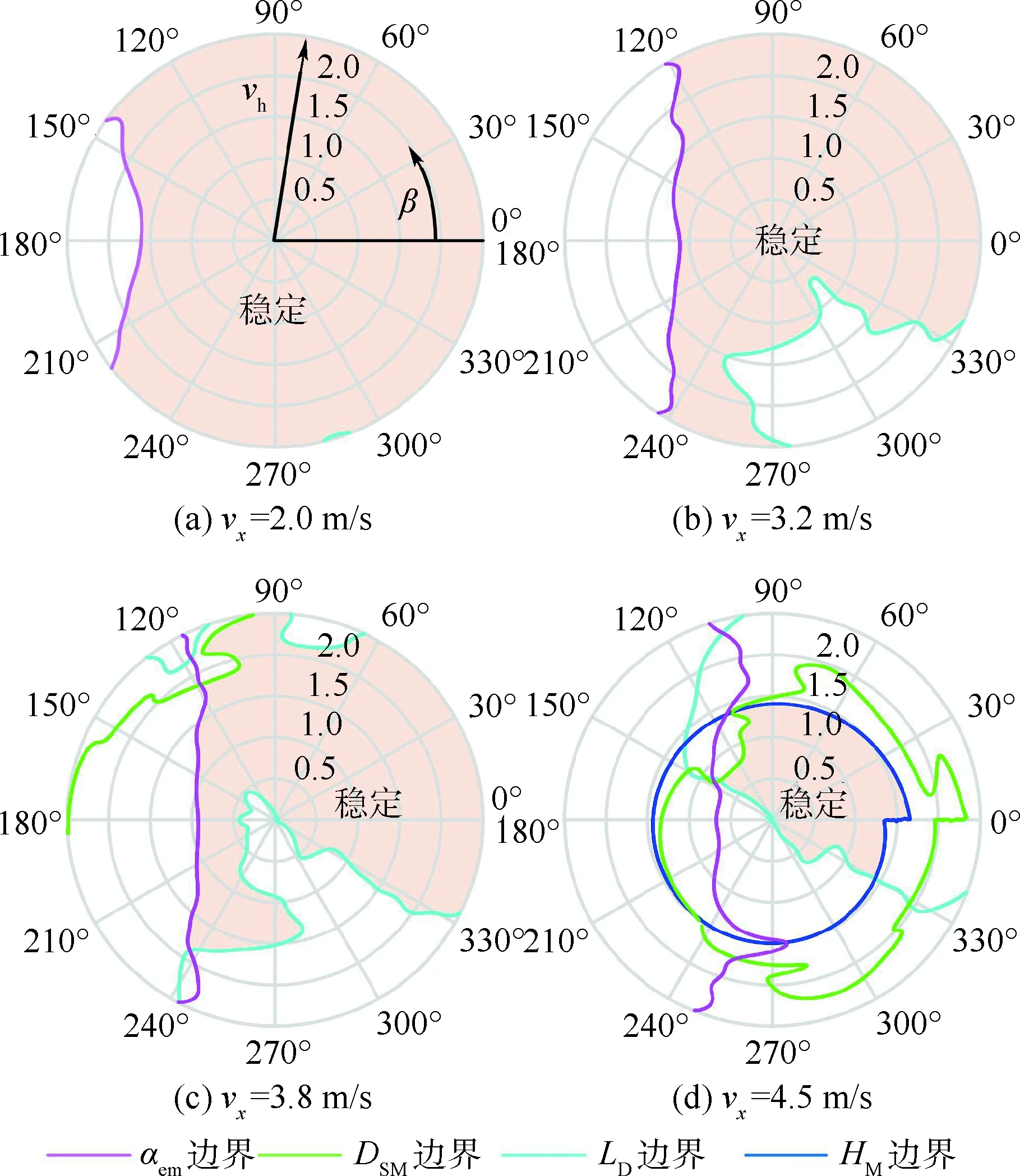
圖11 不同vx下綜合穩(wěn)定性邊界Fig.11 Comprehensive stability boundary under different vx

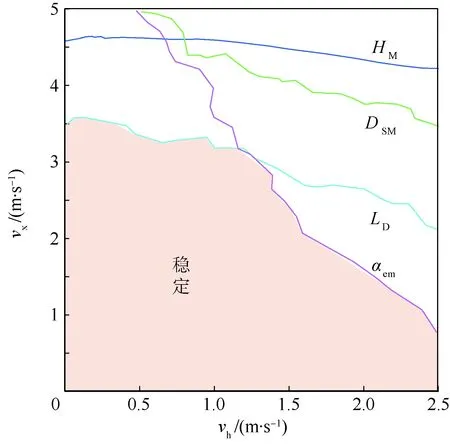
圖12 vx-vh綜合穩(wěn)定性邊界Fig.12 vx-vh comprehensive stability boundary

5 結(jié) 論

本文建立某型著陸器觸地關(guān)機(jī)模式下的動(dòng)力學(xué)仿真模型，著重分析著陸速度對(duì)穩(wěn)定性的影響，得到：

1) 結(jié)合動(dòng)力學(xué)仿真模型及多島遺傳優(yōu)化算法，確定了考慮著陸器水平速度下的極惡劣地形參數(shù)。

2) 基于仿真模型計(jì)算結(jié)果，利用RBF神經(jīng)網(wǎng)絡(luò)建立了反映極惡劣地形下著陸器速度參數(shù)與穩(wěn)定性指標(biāo)值之間映射關(guān)系的代理模型，進(jìn)而計(jì)算得到了軟著陸穩(wěn)定性指標(biāo)的速度穩(wěn)定性邊界，確定了保證著陸器安全軟著陸的速度取值范圍。

3) 本文研究方法具有低成本、高效率等特點(diǎn)，且適用于其他型號(hào)著陸器的研制過程。