階段嗣后充填采場結構參數的多目標多屬性優化

蘭明，劉志祥，李夕兵

?

階段嗣后充填采場結構參數的多目標多屬性優化

蘭明，劉志祥，李夕兵

(中南大學 資源與安全工程學院，湖南 長沙，410083)

為確定某金礦階段嗣后充填采場最優開采參數，采用彈性厚板理論，分析不同跨度下頂柱厚度與最大拉應力的關系；結合礦山實際開采條件，通過中心復合試驗設計及數值模擬計算得到不同結構參數下的力學響應；構建最大拉應力、最大壓應力和最大豎向位移的二階響應面模型，研究各響應量之間的關系；通過多目標優化及多屬性決策的方法最終實現采場結構參數的綜合優化。研究結果表明：頂柱最小厚度為4.00 m；礦柱跨度及頂柱厚度對采場力學響應產生顯著影響，采場最優開采尺寸是礦房跨度為29.90 m，礦柱跨度為31.40 m，頂柱厚度為 5.24 m。

嗣后充填采場；結構參數；數值分析；響應面法；多目標優化；理想點法

隨著硬巖金屬礦山往深部不斷推進，開采技術條件及環境發生改變，淺部開采方法難以適用于礦山后續的深部開采[1]。國內某黃金礦山所采用的淺部采礦方法為上向進路充填法，當開采至?470 m中段左右時，該方法已難以滿足現有的生產要求。為提高生產效率、節約成本及確保安全等，該礦山嘗試采用中深孔落礦階段嗣后充填法并結合上向進路法進行采場試驗。采場進行嗣后充填后，采空區及頂柱暴露面積過大或者暴露時間過長均將帶來安全隱患，為確保試驗采場的有序開采，需確定合理的采場結構參數[2]。數值模擬方法[3?4]是研究采場結構的一種重要手段，它能夠有效地提高設計效率，減少現場試驗所帶來的成本，適用性強。劉欽等[5?7]以單一響應為目標對采場參數進行優化，通過計算得到了采場最佳參數，然而，將不同的響應作為待優化目標，不同優化結果之間極有可能是互相矛盾的，單目標優化容易造成最優解不穩定。多目標優化[8?10]在很大程度上能夠克服單目標優化的不足。MARLER等[11]認為，單目標優化由于目標函數單一，存在唯一最優解，而多目標優化的結果是獲得一系列可行解，這些可行解在理論上均可認為是有效的，只是在工程應用上對于決策者來說實用價值不大，如何在眾多可行解中合理地選擇理想方案是多目標優化所面臨的難題。一些研究者提出將多屬性決策方法如模糊數學、層次分析法及TOPSIS法等作為采礦方法的優選[12?13]，較好地解決了采礦方法的優選問題。為此，本文作者針對現存采場結構參數優化方法的不足，以國內某金礦中深孔分段崩礦階段嗣后充填采場為研究對象，首先通過厚板理論確定合理的采場結構參數范圍，以此為基礎，設計采場結構參數的正交試驗方案，對不同方案下采場開挖進行數值模擬試驗；其次，建立不同參數與其力學響應之間的響應面模型，采用遺傳算法進行多目標優化，獲得相應的可行解；最后，基于多屬性決策的理想點法，綜合考慮各可行解(結構參數)及其力學響應，優選出采場最佳結構參數，以此指導礦山的安全高效開采。

1 工程概況及結構參數方案選擇

1.1 工程概況

某礦V號礦體為設計范圍內主要礦體，賦存于+85~?650 m水平，主要走向為5°~15°，自北向西傾斜，?470 m中段以上即將開采完畢；?470~?510 m為主要開采中段，該中段內礦體較規整，平均厚度為12.5 m，平均傾角為55°；圍巖中等穩固，普氏系數為4~9。根據礦山的開采技術條件及現狀，?470 m中段及其以下礦體變厚，為大規模開采創造了條件。

借鑒中厚礦體中深孔爆破開采相關經驗，采用中深孔落礦階段嗣后充填法對試驗采場進行開采，采場布置見圖1：采場沿礦體走向布置，由礦房及礦柱構成，回采階段高度為40.0 m，寬度為12.5 m。采場上覆為120.0 m高充填體，因此，需留有一定厚度頂柱。脈內靠近下盤附近布置中深孔鑿巖巷道，以切割天井作為首次爆破自由面及補償空間，自上而下分層進行中深孔爆破，底部布置無底柱塹溝出礦結構，采用鏟運機出礦。兩側礦房回采完畢后，對空區進行嗣后充填，然后回收礦柱。

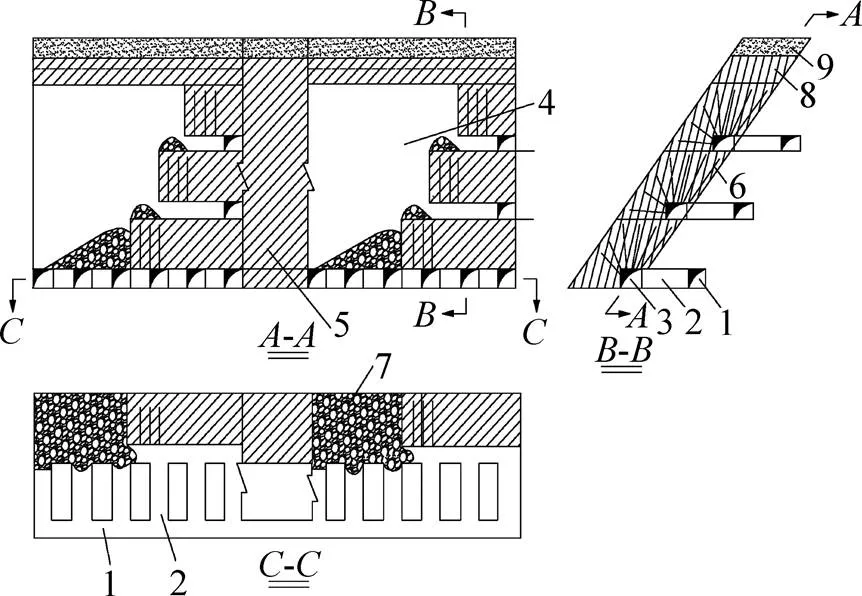
1—脈外運輸巷道；2—出礦巷道；3—分段鑿巖巷道； 4—礦房；5—礦柱；6—中深孔；7—礦石堆； 8—頂板；9—上覆充填體。

1.2 基于厚板理論的開采參數選擇

采用中深孔嗣后充填法開采。在采場充填前，頂柱存在著一定的暴露時間，此時，采場穩定性主要由頂柱的受力狀態決定。國內外許多研究者將彈性薄板理論應用于頂柱受力分析，但深部采場頂柱多數不符合彈性薄板的適用條件，頂柱的厚跨比一般較大，彈性薄板理論難以保證分析結果的可靠性，在這種情況下，采用厚板理論進行分析更符合工程實際。

將采場頂柱簡化為矩形板，設頂柱長邊邊長為，短邊邊長為，板厚度為，頂柱礦巖彈性模量為，泊松比為，密度為，抗拉強度為σt，其力學模型如圖2所示。

按照Vlasov厚板理論[14]，簡支矩形厚板的平衡微分方程為

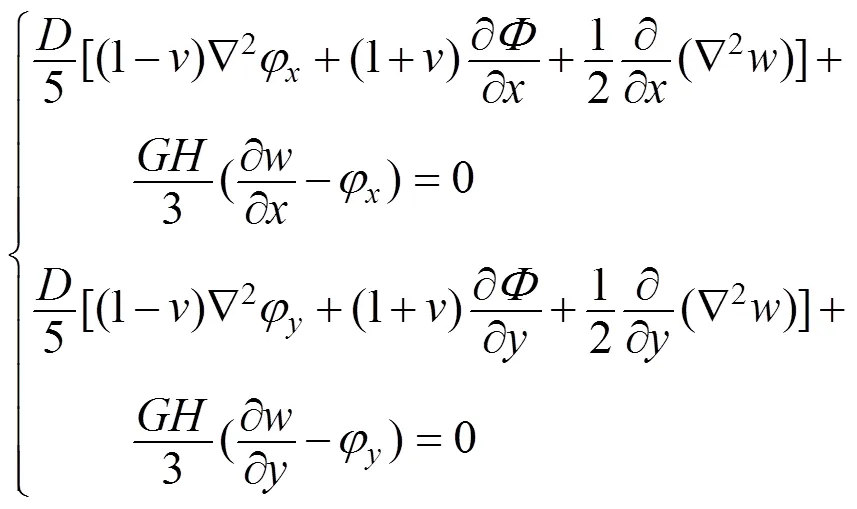
式中：，為頂柱的抗彎剛度；和分別為板在xz和yz截面的轉角；；為

拉普拉斯算子；為頂柱的擾度；為頂柱的剪切模量；為頂柱的厚度。板在和方向的力矩分別為

在考慮邊界扭矩及剪應變的情況下，板的邊界條件為

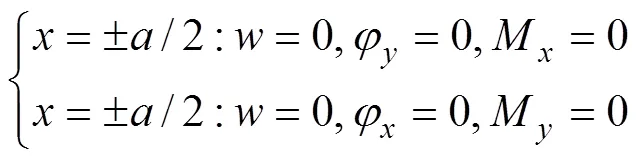
對板的撓度、轉角位移函數和載荷(包括上覆充填體及頂柱自重)進行三角級數展開：

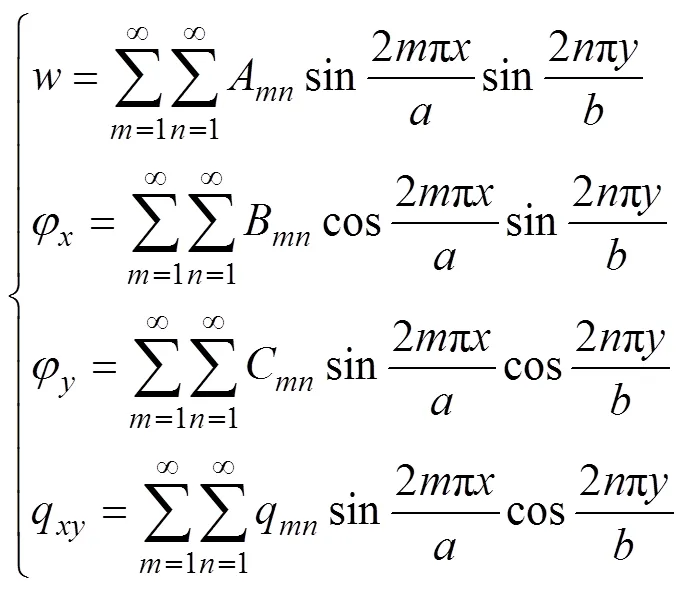
聯立式(1)和(4)得系數A，B，C和q，近似取=1，代入式(2)求得力矩的表達式為

由式(5)可知：M和M在=/4及=/4處取得最大值，不失一般性，可令Mmax=Mmax，則厚板將在下表面出現最大拉應力為

當頂柱受力彎曲過程中最大拉應力超過其抗拉強度時，可認為發生彎曲破壞，因此，式(6)可作為頂柱破壞的判據。根據工程實際，該采場頂柱寬度為礦體厚度，即=12.5 m，礦巖密度=2 810 kg/m3，上覆充填體密度0=1 670 kg/m3，泊松比=0.28，礦巖抗拉強度為2.34 MPa。按相關經驗，取安全系數為2，頂柱跨度范圍設為25~35 m，當頂柱厚度為3~8 m時，通過計算可以獲得不同跨度下頂柱厚度與最大拉應力的關系曲線，見圖3。

跨度/m：1—25.0；2—27.5；3—30.0；4—32.5；5—35.0。

圖3 不同跨度下采場頂柱與最大拉應力關系

Fig. 3 Relationship between stope roof and the maximum in different spans

從圖3可以看出：當厚度超過4 m時，在25~35 m跨度范圍內，頂柱最大拉應力均未超過礦巖的抗拉強度，因此，從安全角度考慮，在采場頂柱為4~8 m時，在采場跨度25~35 m范圍內進行結構參數優化是可行的。

2 數值模擬試驗及目標函數擬合

2.1 數值計算模型

為研究不同參數對采場穩定性影響，對模型進行適當簡化后，取礦體平均厚度為12.5 m，采場階段高度為40.0 m，礦體傾角為55°，上覆充填體高度為120.0 m。采場分為礦房及礦柱采場，兩側礦房開采充填完畢后進行礦柱開采。通過巖體工程地質調查、上下盤圍巖取樣測試及充填體強度試驗，經過工程強度折減后獲得數值模擬所需的巖體力學參數，見表1。原巖應力包括巖體自重應力及構造應力，通過現場測量及地應力的回歸分析，獲得沿礦體走向應力hmax、垂直礦體走向應力hmin以及豎直方向應力z隨著深度的變化規律如下：

根據圣維南原理，數值分析廣泛采用3~5倍開挖半徑作為模型邊界，本文模型長×寬×高取為300 m×160 m×200 m，見圖4。為獲得采場開挖后最大拉應力、最大壓應力、最大豎向位移等力學響應，取礦房及礦柱跨度分別為20.0，25.0和35.0 m，頂柱厚度分別為4.0，6.0和8.0 m，根據中心復合試驗設計原理，共設計15個試驗點進行數值模擬分析，結果見表2。

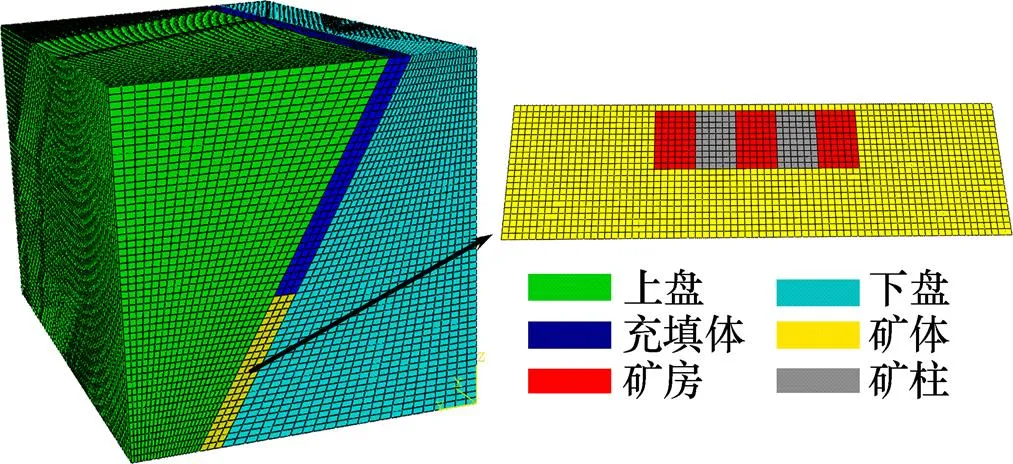
圖4 有限元分析模型

2.2 數值計算結果

從表2可看出：綜合各方案，采場最大壓應力在16.12~19.75 MPa之間，最大拉應力在1.11~1.79 MPa之間，最大豎向位移在4.44×10?2~5.29×10?2 m之間。表2中方案14采場開采后的最小主應力見圖5。從圖5可見：頂柱中部易出現較大拉應力，最大值為 1.682 MPa，未超過礦巖抗拉強度2.340 MPa，采場處于穩定狀態。方案14最大豎向位移見圖6。從圖6可以看出：上、下盤越靠近空區位移越大，頂柱位移較大，最大豎向位移出現在靠近上盤處。總體來說，表2中各方案的力學響應均在合理的安全范圍內，采場未發生破壞。

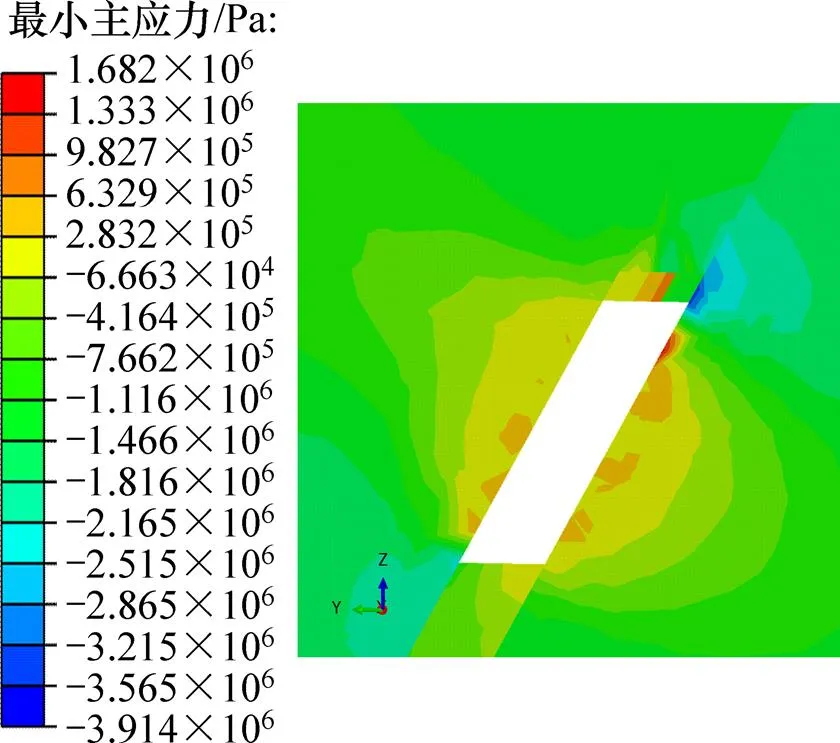
圖5 方案14最小主應力

圖6 方案14最大豎向位移

表1 巖體力學參數

表2 各方案力學響應指標比較結果

2.3 響應面法擬合目標函數

通過響應面法建立礦房跨度、礦柱跨度和頂柱厚度與采場最大壓應力、最大拉應力及最大豎向位移之間的非線性映射關系，采用具有相互作用的二階響應面法[15]，其表達式為

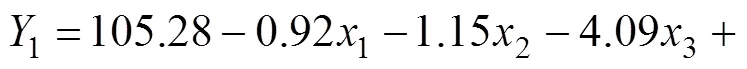
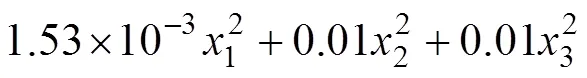
式(9)~(11)中3個響應面函數擬合程度見圖7，相應的復相關系數2分別為0.980 2，0.998 8和0.995 9，由此可見各模型總體擬合度和可靠性均較高。各模型顯著性水平見表3。反映了參數的顯著性[16]，＞0.050 0表示該因素影響不顯著，0.000 1≤≤0.050 0表示該因素影響比較顯著，＜0.000 1表示該因素影響極其顯著。

為了更加直觀反映單因素對各響應的影響，分別對礦房跨度、礦柱跨度及頂柱厚度進行歸一化處理。在分析其中1個因素對某一響應的影響時，保持其他2個因素為均值0.5。最大壓應力隨不同因素變化曲線見圖8(a)，可見最大壓應力隨3個因素增大均呈先減小后增大的趨勢，而當頂柱厚度大于5.2 m(歸一化值為0.3)時，對最大壓應力影響極明顯。

(a) 最大壓應力；(b) 最大拉應力；(c) 最大豎向位移

表3 各模型顯著性水平P

(a) 最大壓應力；(b) 最大拉應力；(c) 最大豎向位移

最大拉應力隨不同因素的變化規律見圖8(b)。從圖8(b)可見：隨著3個因素增加，最大拉應力分別在3個因素的均值附近(即表2中方案8的采場參數值)時達到極小值；此外，礦柱跨度和頂柱厚度對最大拉應力產生顯著影響。

最大豎向應力隨不同因素的變化規律見圖8(c)。從8(c)可見：最大豎向位移隨著礦柱跨度增大而增大，隨著頂柱厚度增大而減小；礦柱跨度變化對最大豎向位移幾乎沒影響；礦柱跨度和頂柱厚度對最大豎向位移影響較顯著，礦柱跨度增大使得最大豎向位移急劇增加；頂柱厚度增大有利于減小采場最大豎向位移。

3 結構參數多目標多屬性優化

3.1 結構參數多目標優化的Pareto解

采場結構參數優化應該基于在保證安全的前提下，力學響應最小化的原則。但一般來說，各結構參數與不同力學響應之間存在非線性關系，同時滿足各個目標函數的最優解幾乎不存在。LIN等[17?20]提出利用Pareto最優的概念解決多目標優化問題，其中，Pareto解的定義為：對于多目標優化問題，

1，2∈R，對所有目標函數均有f(1)≤f(2)，且存在f(1)＜f(2)(其中，=1，2，…，)，則解1支配2，記為1＞2。若R中不存在解和使得＞，則為R中的非支配解，這樣的解就是Pareto最優解。Pareto最優解往往以集合的形式出現，其構成的子空間為Pareto前沿面。

基于以上原則，采用多目標遺傳算法對式(9)~(11)在礦房、礦柱跨度25~35 m以及頂柱厚度4~8 m范圍內進行參數尋優。遺傳算法初始參數為：種群數量=30；最大進化代數iter=500；交叉概率c=0.9；變異概率m=0.1。經過121次迭代，獲得采場參數多目標優化問題的Pareto最優解集與其對應力學響應值，見表4。通過式(13)對表4中Pareto解對應的響應值進行歸一化處理得到Pareto二維前沿面，如圖9所示。

從表4及圖9可以看出：所求得的可行解集完全符合Pareto非劣解的定義，這也驗證了對于采場結構參數的多目標優化問題，獲得單一最優解是不現實的，有必要對這些可行解進行進一步優選。

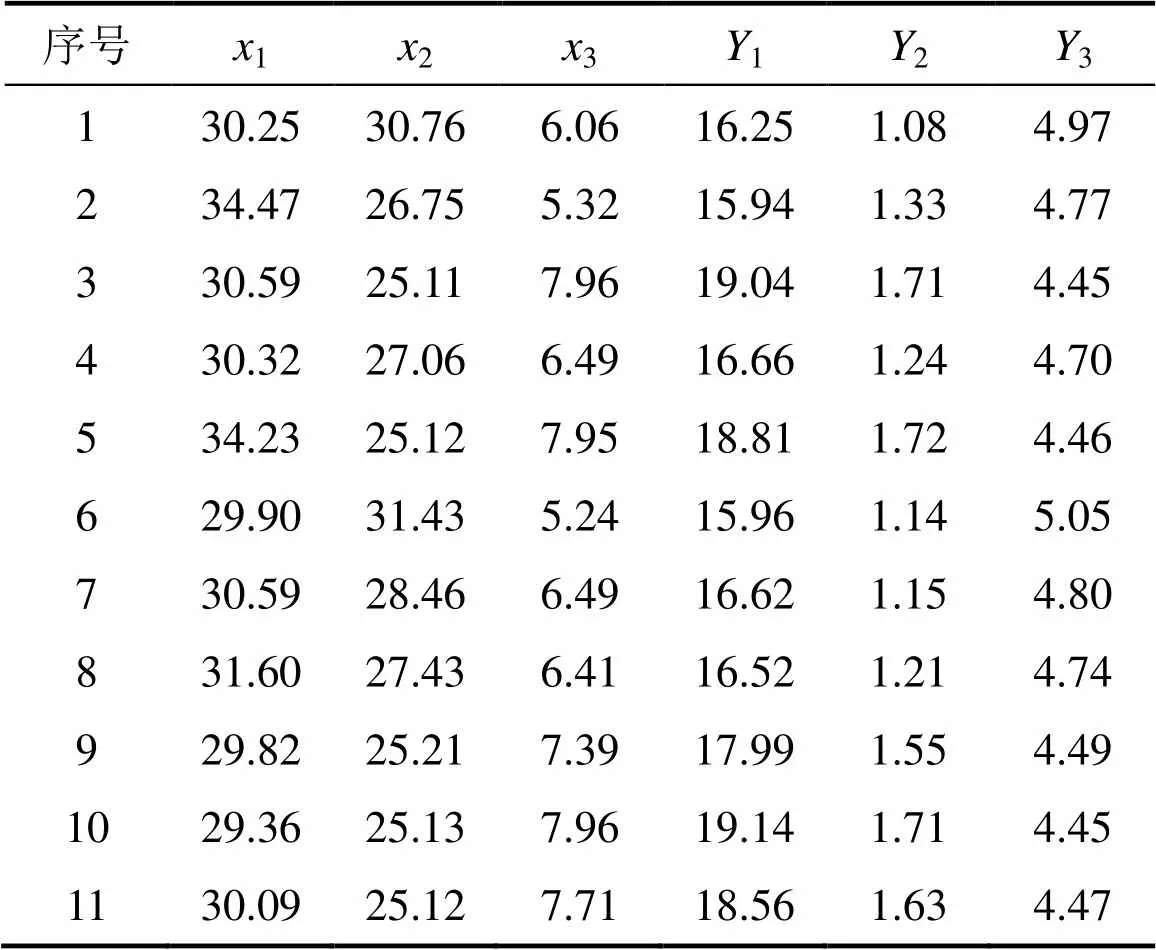
表4 Pareto最優解集及其力學響應

3.2 基于多屬性優選的結構參數確定

對于中深孔嗣后充填采場來說，礦房跨度、礦柱跨度及頂柱厚度往往與生產效益有密切關系，而力學響應對應開采安全性。一方面，跨度越大，采場一次出礦量增大，頂柱厚度越小，礦石損失越小，增大跨度及減小頂柱厚度能提高采場生產效率，減小礦石損失；另一方面，隨著開挖進行，采場受力及變形情況須保持在安全穩定范圍內，這在一定程度上與增大跨度、減小頂柱厚度是相矛盾的。故為了確定合理的結構參數，應兼顧這2個方面因素的影響。理想點法(TOPSIS)是通過計算評價對象與理想目標之間的接近程度，實現多目標決策分析的一種常用方法。基于理想點綜合評價法，對表4中各參數方案進行優選，其實現步驟如下[21?23]。

1) 建立初始評價矩陣。將表4中礦房、礦柱跨度及頂柱厚度即1，2和3作為經濟指標，采場最大壓應力、最大拉應力及最大豎向位移即1，2和3作為安全指標，由此構建初始評價矩陣為

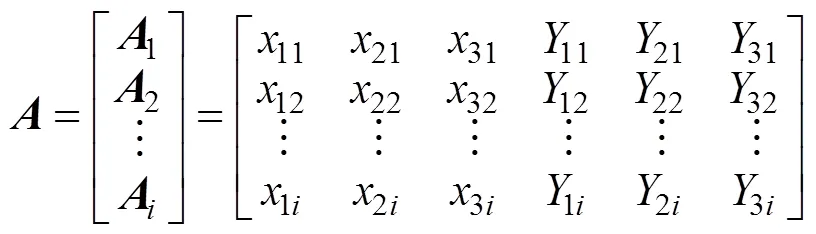
式中：為初選方案的指標向量集，=11。

2) 規范化評價矩陣。在評價矩陣式(14)中，礦房、礦柱跨度(1i和2i)為效益型指標，其值越大越好；其余各指標為成本型指標，其值越小越好。對矩陣進行歸一化處理后得到新的評價矩陣：

3) 評價指標權重的確定。采用AHP及熵權法的主客觀的組合賦權方法，獲得各指標的組合權重=(0.039，0.125，0.67，0.033，0.107，0.028)。

5) 方案貼近度計算。分別計算評價對象到正、負理想解的歐式距離，其計算公式如下：

則Z與理想解的貼近度為

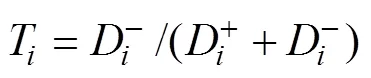
式(19)中T在區間[0，1]內，其值越大，表示越貼近理想解。

6) 結構參數的確定。經過式(17)~(18)計算得到表4中各方案的貼近度如圖10所示。

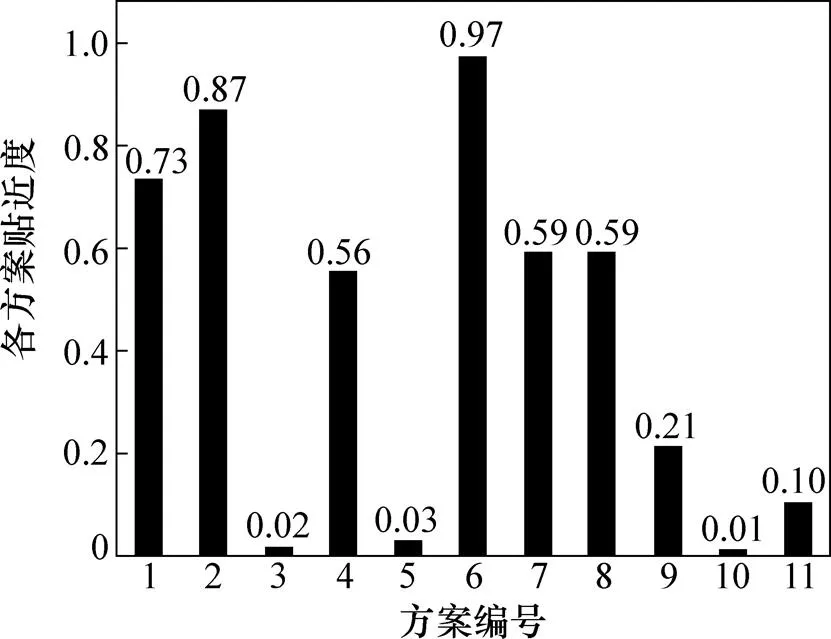
圖10 各方案貼近度

從圖10可以看出：表4中方案6在所有方案中的貼近度最高，達0.97。綜合考慮安全性及經濟性的影響，最終確定如下采場最佳開采參數：礦房跨度為29.90 m，礦柱跨度為31.43 m，頂柱厚度為5.24 m。

4 結論

1) 采用Vlasov厚板理論分析了頂柱的力學特性，得到了不同跨度下頂柱厚度與最大拉應力的關系，確定礦房、礦柱跨度在25~35 m范圍內，頂柱最小厚度為4.00 m。

2) 頂柱底部中間處易產生較高拉應力及豎向位移，上、下盤靠近空區附近易出現較大變形，采場最大壓應力為19.750 MPa，最大拉應力為1.682 MPa，最大豎向位移為5.28 cm，采場處于穩定狀態。

3) 礦柱跨度及頂柱厚度對采場最大壓應力、最大拉應力及最大豎向位移產生顯著影響。

4) 通過多目標優化將產生一系列的Pareto非劣解，基于多目標決策的TOPSIS法綜合考慮結構參數與力學響應的作用，經各方案優劣度排序獲得最優貼近度為0.97。確定采場最佳開采尺寸如下：礦房跨度為29.90 m，礦柱跨度為31.43 m，頂柱厚度為5.24 m。

[1] 李夕兵, 姚金蕊, 宮鳳強.硬巖金屬礦山深部開采中的動力學問題[J]. 中國有色金屬學報, 2011, 21(10): 2551?2563. LI Xibing, YAO Jinrui, GONG Fengqiang, et al. Dynamic problems in deep exploitation of hard rock metal mines[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(10): 2551?2563.

[2] 汪偉, 羅周全, 秦亞光, 等. 無底柱深孔后退式崩礦法采場結構參數優化[J]. 東北大學學報(自然科學版), 2016, 37(4): 578?582. WANG Wei, LUO Zhouquan, QIN Yaguang, et al. Stope parameters optimization of non-pillar longhole retreat caving[J]. Journal of Northeastern University(Natural Science), 2016, 37(4): 578?582.

[3] 張建明, 陳順滿. 基于數值模擬的某銅礦深部采場結構參數優化研究[J]. 化工礦物與加工, 2016(12): 47?51. ZHANG Jianming, CHEN Shuman. Optimization of structural parameters for deep stope in a copper mine based on numerical simulation[J]. Industrial Minerals & Processing, 2016(12): 47?51.

[4] 陶干強, 孫冰, 宋麗霞, 等. 充填法采場結構參數優化設計[J]. 采礦與安全工程學報, 2009, 26(4): 460?464. TAO Ganqiang, SUN Bing, SONG Lixia, et al. Optimal design of stope structural parameters using back-filling method[J]. Journal of Mining & Safety Engineering, 2009, 26(4): 460?464.

[5] 劉欽, 劉志祥, 劉愛華, 等. 金礦采場結構參數混沌優化[J]. 采礦與安全工程學報, 2010, 27(4): 548?552. LIU Qin, LIU Zhixiang, LIU Aihua, et al. Chaotic optimization of structural parameters in gold mining field[J]. Journal of Mining & Safety Engineering, 2010, 27(4): 548?552.

[6] 來興平, 蔡美峰, 張冰川. 神經網絡計算在采場結構參數分析中的應用[J]. 煤炭學報, 2001, 26(3): 245?248. LAI Xingping, CAI Meifeng, ZHANG Bingchuan. Application of nonlinear neural network to analyze the stope structure parameters[J]. Journal of China Coal Society, 2001, 26(3): 245?248.

[7] 彭康, 李夕兵, 彭述權, 等. 基于響應面法的海下框架式采場結構優化選擇[J]. 中南大學學報(自然科學版), 2011, 42(8): 2417?2422.PENG Kang, LI Xibing, PENG Shuquan, et al. Optimization of frame stope structure parameters based on response surface method in under-sea mining[J]. Journal of Central South University(Science and Technology), 2011, 42(8): 2417?2422.

[8] 程文淵, 崔德剛. 基于Pareto遺傳算法的復合材料機翼優化設計[J]. 北京航空航天大學學報, 2007, 33(2): 145?148. CHENG Wenyuan, CUI Degang. Optimization for composite wing based on Pareto genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(2): 145?148.

[9] 張永, 吳曉蓓, 徐志良, 等. 基于Pareto多目標遺傳算法的模糊系統設計[J]. 南京理工大學學報, 2007, 31(4): 430?434. ZHANG Yong, WU Xiaobei, XU Zhiliang, et al. Design of fuzzy systems based on pareto multi-objective genetic algorithm[J]. Journal of Nanjing University of Science and Technology, 2007, 31(4): 430?434.

[10] DELGARM N, SAJADI B, KOWSARY F, et al. Multi-objective optimization of the building energy performance:a simulation-based approach by means of particle swarm optimization (PSO)[J]. Applied Energy, 2016, 170: 293?303.

[11] MARLER R T, ARORA J S. Survey of multi-objective optimization methods for engineering[J]. Structural & Multidisciplinary Optimization, 2004, 26(6): 369?395.

[12] 李潔慧, 王新民, 張欽禮, 等. 采場結構參數的層次分析和模糊數學綜合評價[J]. 化工礦物與加工, 2009, 38(9): 23?27. LI Jiehui, WANG Xinmin, ZHANG Qinli, et al. Stope structural parameters optimization based on AHP and fuzzy mathematics[J]. Industrial Minerals and Processing, 2009, 38(9): 23?27.

[13] 趙國彥, 唐洋, 劉志祥, 等. 基于改進的AHP-TOPSIS評判模型的盛大鐵礦采礦方法優選[J]. 科技導報, 2014, 32(3): 25?28.ZHAO Guoyan, TANG Yang, LIU Zhixiang, et al. Mining method optimization of Shengda iron ore based on improved AHP-TOPSIS evaluation model[J]. Science & Technology Review, 2014, 32(3): 25?28.

[14] 何福保, 沈亞鵬. 板殼理論[M]. 西安: 西安交通大學出版社, 1993: 182?187. HE Fubao, SHEN Yapeng. Theory of plates and shells[M]. Xi’an: Xi’an Southwest Jiaotong University Press, 1993: 182?187.

[15] 趙國彥, 馬舉, 彭康, 等. 基于響應面法的高寒礦山充填配比優化[J]. 北京科技大學學報, 2013, 35(5): 559?565.ZHAO Guoyan, MA Ju, PENG Kang, et al. Mix ratio optimization of alpine mine backfill based on the response surface method[J]. Journal of University of Science and Technology Beijing, 2013, 35(5): 559?565.

[16] BUKZEM A L, SIGNINI R, SANTOS D M, et al. Optimization of carboxymethyl chitosan synthesis using response surface methodology and desirability function[J]. International Journal of Biological Macromolecules, 2016, 85: 615?624.

[17] LIN H Y, LIN C J, HUANG M L. Optimization of printed circuit board component placement using an efficient hybrid genetic algorithm[J]. Applied Intelligence, 2016, 45(3): 1?16.

[18] JIANG Shouyong, YANG Shengxiang. A Strength pareto evolutionary algorithm based on reference direction for multi-objective and many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(3): 329?346.

[19] 胡旺, YEN G G, 張鑫. 基于Pareto熵的多目標粒子群優化算法[J]. 軟件學報, 2014(5): 1025?1050. HU Wang, YEN G G, ZHANG Xin. Multi-objective particle swarm optimization based on pareto entropy[J]. Journal of Software, 2014, 25(5): 1025?1050.

[20] 喬俊飛, 魏靜, 韓紅桂. 基于改進NSGA2算法的給水管網多目標優化設計[J]. 控制工程, 2016, 23(12): 1861?1866.QIAO Junfei, WEI Jing, HAN Honggui. Multi-objective optimization of water distribution system based on an improved NSGA2 algorithm[J]. Control Engineering of China, 2016, 23(12): 1861?1866.

[21] 張楚旋, 李夕兵, 董隴軍, 等. 微震監測傳感器布設方案評價模型及應用[J]. 東北大學學報(自然科學版), 2016, 37(4): 594?598. ZHANG Chuxuan, LI Xibing, DONG Longjun, et al. Evaluation model of microseismic monitoring sensor layout scheme and its application[J]. Journal of Northeastern University(Natural Science), 2016, 37(4): 594?598.

[22] AKBARI M, SHOJAEEFARD M H, ASADI Parviz, et al. Hybrid multi-objective optimization of microstructural and mechanical properties of B 4 C/A356 composites fabricated by FSP using TOPSIS and modified NSGA-II[J]. Transactions of Nonferrous Metals Society of China, 2017, 27(11): 2317?2333.

[23] 申毅榮, 解建倉. 基于熵權和TOPSIS法的水安全模糊物元評價模型研究及其應用[J]. 系統工程, 2014(7): 143?148. SHEN Yirong, XIE Jiancang. Fuzzy Matter-element model for evaluating of water safety based on entropy weight and TOPSIS and application[J]. Systems Engineering, 2014(7): 143?148.

Multi-objective optimization and multi-attribute decision making on structural parameters of stage backfilling stope

LAN Ming, LIU Zhixiang, LI Xibing

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

In order to determine the optimum dimensions of the stage backfilling stope of a gold mine, the relationship between the roof thickness and the maximum tensile stress under different spans was analyzed by using the elastic thick plate theory. With consideration of the actual mining conditions of the mine, the mechanical responses under different structural parameters were obtained by means of the central composite test design and the numerical simulation. In addition, the second order response surface models of the maximum tensile stress, the maximum compressive stress and the maximum vertical displacement were performed to investigate the relationship among each response. Finally, the comprehensive optimization of stope structural parameters was realized with the multi-objective optimization and the multi-attribute decision making method. The results show that the minimum roof thickness is 4.00 m. The pillar span and roof thickness have significant impact on the mechanical response. The optimal parameters are determined as follows: the scheme of chamber span is 29.90 m, the pillar span is 34.10 m and the roof thickness is 5.24 m.

stage backfilling stope; structure parameters; numerical analysis; response surface method; multi-objective optimization; ideal point method

10.11817/j.issn.1672?7207.2019.02.017

TD853

A

1672?7207(2019)02?0375?09

2018?03?05；

2018?05?21

國家自然科學基金重點資助項目(41630642)；國家自然科學基金資助項目(51674288)；湖南省研究生科研創新項目(CX2016B052)(Project(41630642) supported by the National Natural Science Key Foundation of China; Project(51674288) supported by the National Natural Science Foundation of China；Project(CX2016B052) supported by the Graduate Research Innovation Program of Hunan Province)

劉志祥，博士生導師，從事金屬礦山開采及災害防控技術研究；E-mail：CSU_LM@163.com

(編輯 陳燦華)