六支鏈輪腿式月面機器人機構優化設計
李 聰,韓亮亮,袁 帥,張元勛
(1. 上海宇航系統工程研究所,上海 201108; 2. 上海市空間飛行器機構重點實驗室,上海 201108; 3. 重慶大學 機械工程學院,重慶 400044; 4. 南京航空航天大學航天學院, 南京 210016)
1 引言
月球是人類開展深空探測的起點,而月面機器人將在月球探測活動中扮演著至關重要的角色[1]。月球的主要地形有環山、月海、月陸和山脈等,月面機器人要在此環境中作業就必須具備一定的越障能力。目前月面機器人行走方式主要有輪式、腿式、履帶式以及復合式[2],其中輪腿復合式移動機構融合了輪式移動機構高速高效及腿式移動機構復雜地形適應能力強的優點,但機構相對復雜、移動性能參數在不同構型狀態下有所變化。因此,有必要開展輪腿式機器人構型尺寸及可調構型參數與運動性能關系的研究,以獲取更優的運動性能。
目前針對輪腿式月面機器人機構的研究多在構型設計、步態規劃等方面,在輪式移動性能構型優化方面的研究尚較少。本文針對此問題,以六支鏈輪腿式月面機器人為研究對象,以機器人爬坡這一典型越障工況為輸入條件,通過ADAMS建立參數化分析模型,研究輪腿尺寸參數與腿部角度與爬坡驅動力的關系,優化配置參數。
2 六支鏈輪腿式月面機器人
輪腿式月面機器人可抽象為懸架、輪腿和車身三部分[3-4],構型為在六個方向上都具有對稱結構的正六邊形布局,在傳統三個自由度之外另有一個轉動副,可使車輪能繞著上一關節整周旋轉。六支鏈輪腿機構構型及組成如圖1所示,其單腿機構構型及組成如圖2所示。
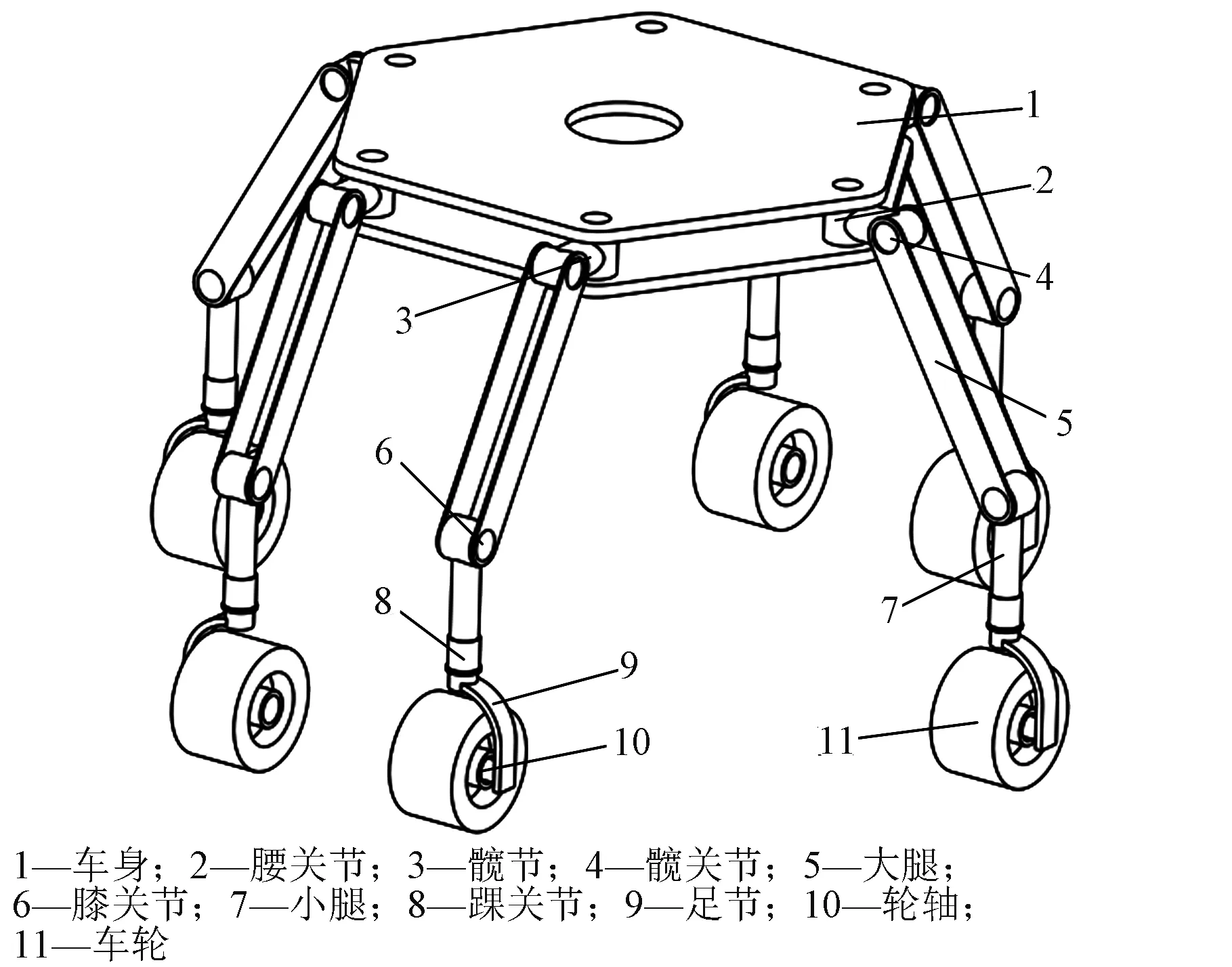
圖1 六支鏈輪腿式月面機器人機構示意圖Fig.1 Schematic diagram of six branched wheel-legged lunar robots
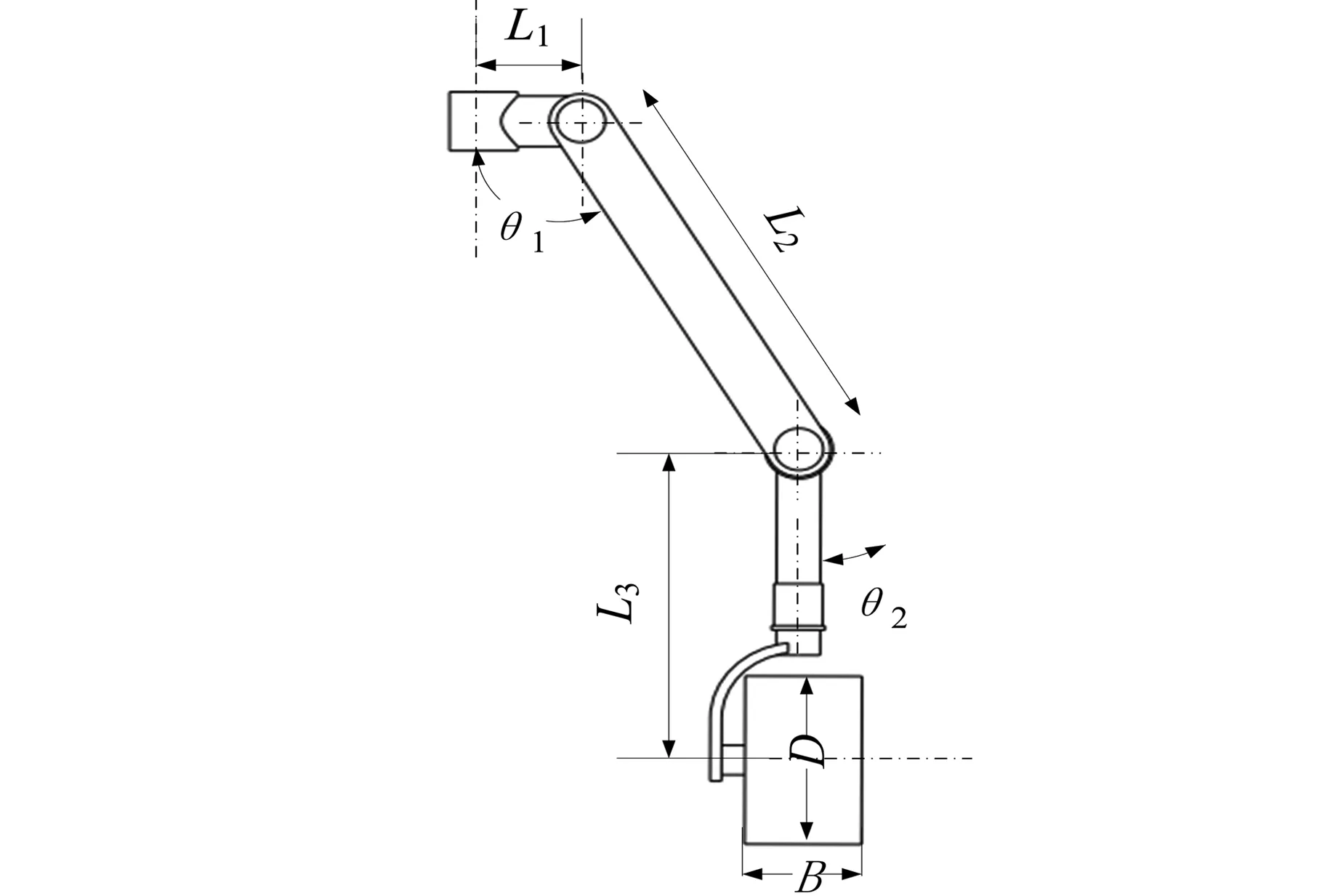
圖2 機器人輪腿機構簡圖Fig.2 Sketch of the mechanism of the robot wheel leg
3 參數化模型
建立六支鏈輪腿式月面機器人單腿結構及坐標系如圖3所示,單腿初始位置設置為腰關節軸線J1與車身上下平面垂直,大腿垂直向下,小腿軸線J4與J1平行,車輪朝向前進方向。腿部建立的四個坐標系分別為基坐標系Oxyz、髖關節坐標系O1x1y1z1、膝關節坐標系O2x2y2z2、踝關節坐標系O3x3y3z3以及輪腿末端坐標系O4x4y4z4。
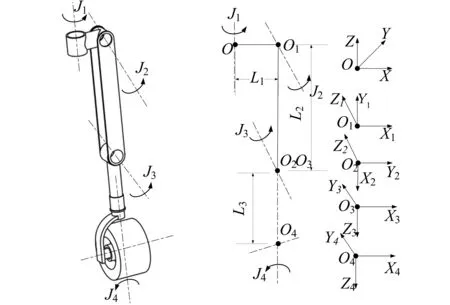
圖3 機器人腿部坐標系建立示意圖Fig.3 Schematic diagram of the robot's leg coordinate system
根據所建立的機器人腿部坐標系、設定的輪腿桿長及關節角數據得出六支鏈輪腿式月面機器人腿部D-H參數表(表1)。

表1 機器人腿部D-H參數表
六支鏈輪腿式月面機器在斜坡上移動的受力情況可簡化如圖4所示。定義正六邊形車身的外接圓直徑為D0,則機器人初始狀態輪腿分布如圖5所示,其中β為機器人大腿分布角,圖中為60°,V為速度。
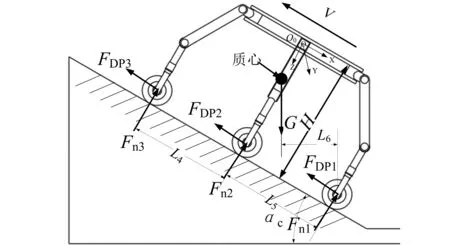
圖4 機器人坡面行駛受力示意圖Fig.4 Schematic diagram of the force on the slope of the robot

圖5 六支鏈輪腿式月面機器人爬坡位姿示意圖Fig.5 Schematic diagram of the climbing posture of Six branched wheel-legged lunar robot
由圖1易知機器人質心坐標X=Y=0。假設六支鏈輪腿式月面機器人各組成部分質量均勻,可定義車身與腰關節與髖關節以及髖節的質量為G1,大腿質量為G2,膝關節與小腿與踝關節與踝節質量為G3,車輪質量為G4。令G1位于車身坐標原點,大腿質心位于其幾何中心位置,G3位于小腿長度中心位置處,G4位于車輪軸心位置。則可知六支鏈輪腿式月面機器人在圖5狀態下質心Zc的坐標為式(1):
(1)
定義爬坡中后輪輪心指向質心為一觀測向量,則觀測向量在水平面上的投影方向與爬坡速度方向相同時,即為六支鏈輪腿式月面機器人爬坡時不產生傾覆的必要條件,即L6≥0推導可得六支鏈輪腿式月面機器人爬坡不傾覆的必要條件為式(2):
(2)
由式(2)可知輪腿桿長及關節角是影響六支鏈輪腿式月面機器人爬坡穩定性的主要變量。
4 仿真優化
輪式月面機器人的爬坡能力一般優于20°,因此本文六支鏈輪腿式月面機器人以爬30°斜坡作為計算工況,根據式(2)中的設計變量,通過ADAMS對六支鏈輪腿式月面機器人進行參數分析與優化。
根據月面機器人初始設計參數設定參數化模型的初始值L2為490 mm、L3為350 mm、θ1為0°,由于小腿軸線與車身軸線平行,故小腿的俯仰角θ2與大腿的俯仰角θ1關系為θ2=θ1-90°。通過對點的參數化實現對六支鏈輪腿式月面的機器人大腿長度L2、小腿長度L1、小腿俯仰角θ2的參數化。其它機器人參數按照設計值設置如表2所示。在ADAMS的優化設計中以驅動力最小為優化目標,由于機器人爬坡過程中后輪受力最大,如圖6所示,故以機器人后車輪轉矩為優化對象。
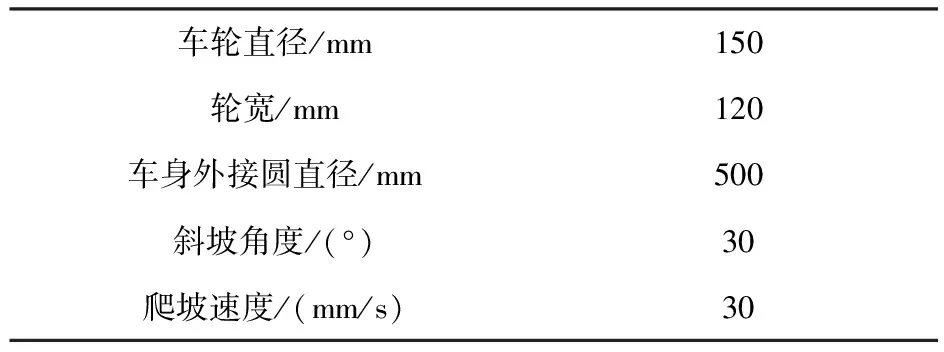
表2 仿真模型參數設置
在ADAMS中運行“設計研究”,即設計變量只有一個在其變化范圍內取不同值時,目標函數的變化情況[7]。分析設計變量大腿長度(圖7中ARM1_2Z)、小腿長度(圖7中xt_l)、小腿俯仰角(圖8中DV_1)的參數化對目標函數的靈敏度,可知所設置的設計變量對六支鏈輪腿式月面機器人后輪驅動力有較高的靈敏度,在機器人的設計與控制中應重點關注。
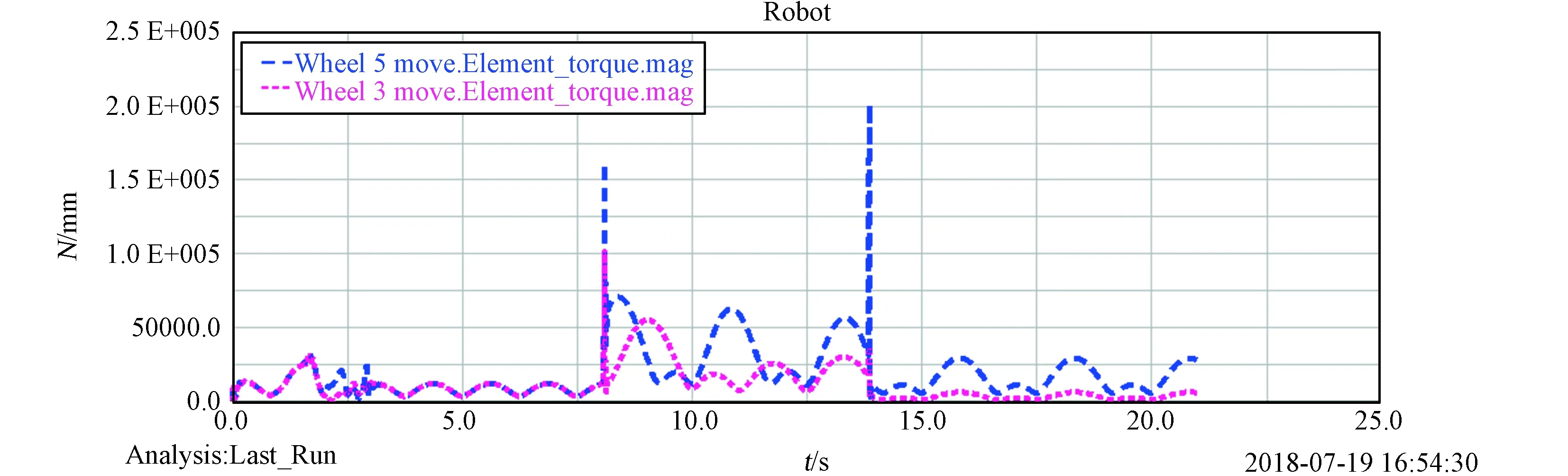
圖6 機器人爬坡中前輪與后輪轉矩曲線圖Fig.6 Torque curve of front and rear wheels in the climbing robot
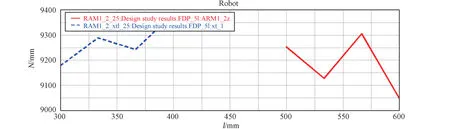
圖7 設計變量ARM1_2Z及xt_l對目標函數的敏感度曲線圖Fig.7 Sensitivity curve of design variables ARM1_2Z and xt_l to the objective function
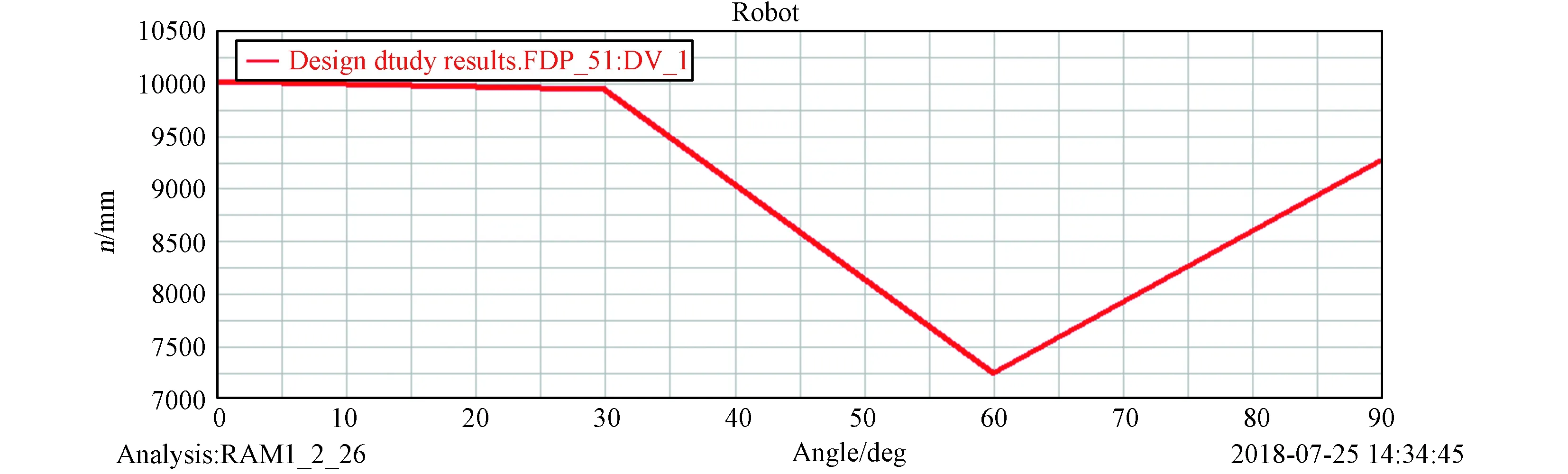
圖8 設計變量DV_1對目標函數敏感度曲線圖Fig.8 Sensitivity curve of design variables DV_1 to the objective function

圖9 目標函數值與迭代次數曲線圖(橫坐標為迭代次數、縱坐標為轉矩)Fig.9 Graph of objective function value and iteration number
優化分析前先進行“實驗設計”,即研究設計變量取不同的可能組合時目標函數的取值情況[7],結果如圖9所示,其最優結果對應的設計變量為大腿最優長度為486 mm、小腿長度為314 mm、大腿俯仰角為90°,此時大腿平行于車身,小腿垂直于大腿,此時機器人爬坡的狀態如圖10所示。
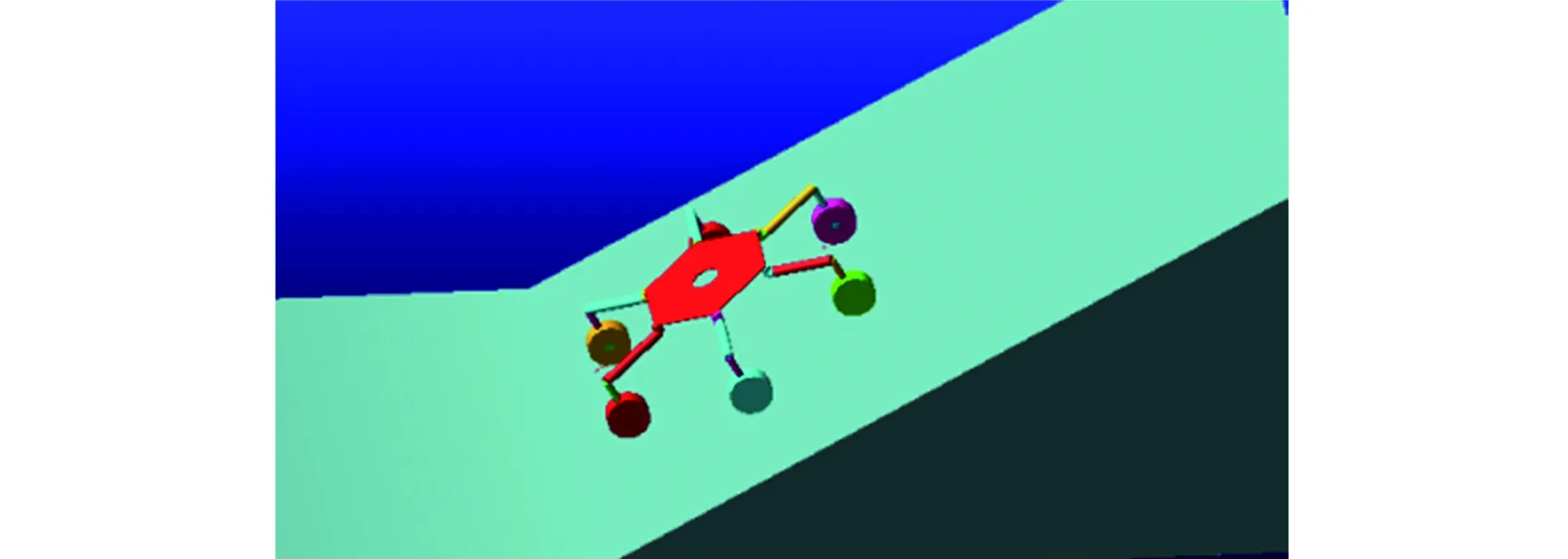
圖10 六支鏈輪腿式月面機器人最優解下姿態Fig.10 Attitude of the optimal solution of a six branched wheel-legged robot
5 結論
本文開展了六支鏈輪腿式月面機器人構型及機構參數化優化設計,參數化設計及仿真表明輪腿機構尺寸參數及關節角參數對機器人影響明顯,在機器人的設計與控制中應重點關注或動態調整;通過參數化優化設計的方法,優化計算得出了較優的機構尺寸及關節角參數,結論及方法可以用于指導工程產品設計。

