艙外航天服-航天員下肢系統動力學建模與分析

林如海，謝曉梅，李鈺新，李學生，王振偉，徐利梅，王 梟

(電子科技大學航空航天學院，成都 611731)

1 引言

隨著載人航天技術和深空探測技術的發展，未來航天員在月球、火星等地外星體表面開展資源勘探、基地建設和科學實驗等出艙活動將是載人空間探測的重要組成部分。充壓航天服為航天員出艙活動提供生命安全保障的同時，由于航天服充壓后變硬及運動關節阻力矩的存在，將增加航天員的工作負荷、降低其工作效率[1-3]。因此，航天服活動性是航天服設計時需要考慮的重要因素之一。

迄今為止，航天員出艙活動大多屬于太空作業，僅有美國在1961年到1972年期間成功進行了月面出艙活動。在執行太空出艙活動作業時，航天員下肢通常使用腳限制器來固定和穩定身體，操作任務主要通過上肢動作完成。隨著航天服的不斷改進，現有航天服上肢系統已具備了一定程度的活動性，但對航天服下肢系統活動性的關注度較少。未來的月球或火星探測任務，航天員進行艙外活動的時間更長、行進距離更遠、作業任務更多更復雜，對艙外航天服上下肢系統的活動性提出了更高的要求[4]。如何提高航天服下肢系統的活動性，保證航天員著艙外航天服后具有行走移動能力將是未來航天服需要攻克的問題之一。

航天員在低重力環境下執行出艙作業任務時，艙外航天服對航天員作業能力的影響目前較多通過地面模擬實驗進行研究，如拋物線飛行、中性浮力水池、氣浮臺等物理方法[5]。為了克服地面模擬技術難度大、實驗成本高、時間周期長和操作風險高等問題，理論建模和數值仿真方法得到了部分學者的關注。早在1998年前后，Newman等就針對微重力下航天員運動的動力學問題開展了研究，在建立的多段人體模型的基礎上，利用試驗測試數據進行了運動學和動力學分析，填補理論航天員艙外活動定量分析的空白[6-7]。Rahn利用建立的艙外航天服動態模型，對多姿態艙外活動進行了模擬仿真[8]。王娟和莊達民采用拉格朗日方程法對失重人體建立了反向運動學和動力學模型，以模擬STS-63任務為例，確定了人體運動做功最少的關節活動范圍[9]。楊峰等將人體模型簡化為桿架模型，結合人體運動學和動力學，利用提出的力矩比優化方法對航天員出艙活動人體上肢運動進行了虛擬控制，估算了出艙活動作業時航天員上肢各關節的力矩[10]。李昊等就現有的航天員艙外太空作業動力學建模與仿真方法進行了探討，建立了一套支持航天員艙外太空作業動力學仿真的軟件平臺，但未對著服航天員開展星表探測出艙活動進行模擬[11]。

為了較好適應未來星表環境下的探測任務需求，航天服下肢關節系統對航天員出艙作業能力的影響將為設計與評價艙外航天服性能提供依據。本文依據人體生理結構，建立航天服-航天員下肢系統簡化物理模型，進行動力學分析；以步態行走、上下樓梯等典型下肢運動為對象，參考美國艙外活動單元(Extravehicular Mobile Unit，EMU)公開數據，對航天服質量、慣性和關節阻力矩對航天員下肢關節運動的作用影響進行數值仿真分析。

2 航天服-航天員下肢系統運動學分析

2.1 物理模型的建立

航天員在執行星表探測作業任務時，直立行走、彎腰拾物、屈膝等動作的實現都需要人體下肢各關節的參與配合。因此本文根據人體生理結構，考慮星表探測過程中肢體動作的多樣性，配置航天服下肢系統髖關節、膝關節及踝關節的自由度分別為3、1、2。

根據我國現有航天員的身高體重參數，擬定航天員的身高為170 cm，體重為65 kg。人體下肢系統各體段的長度、質量和轉動慣量的確定參考GB 10000-88(中國成年人人體尺寸)[11]和GB/T17245-2004(成年人人體慣性參數)[12]。

考慮到美國EMU航天服一直作為國際空間站的艙外航天服，而且公開數據較多，本文以該航天服為研究對象，確定對應的物理模型。EMU航天服下肢物理模型主要包括三個關鍵特性：質量、慣量和服裝關節力矩[13]。其中，服裝關節力矩具有極強的遲滯效應。航天服-航天員下肢物理模型中各項參數如表1所示。

2.2 運動學分析

2.2.1 正運動學分析

基于D-H參數法，在下肢各個關節處建立對應的下肢關節坐標系，如圖1所示。其中，髖關節、膝關節和踝關節分別配置有3、1和2個自由度。

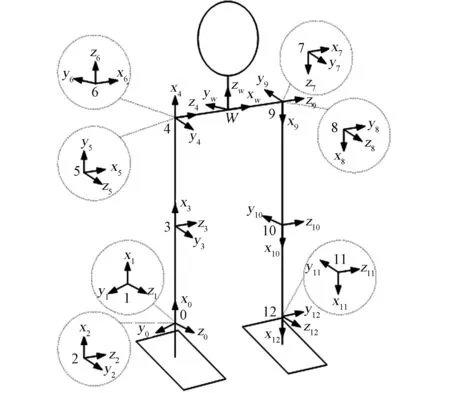
圖1 下肢D-H模型Fig.1 D-H model of lower limbs

根據建立的坐標系及物理模型，確定下肢的D-H參數表，如表2所示。其中,l1是大腿的長度，l2是小腿的長度，l4是腰部的長度。θi是第i個關節自由度繞對應軸的旋轉角度，取決于對應關節的運動范圍。

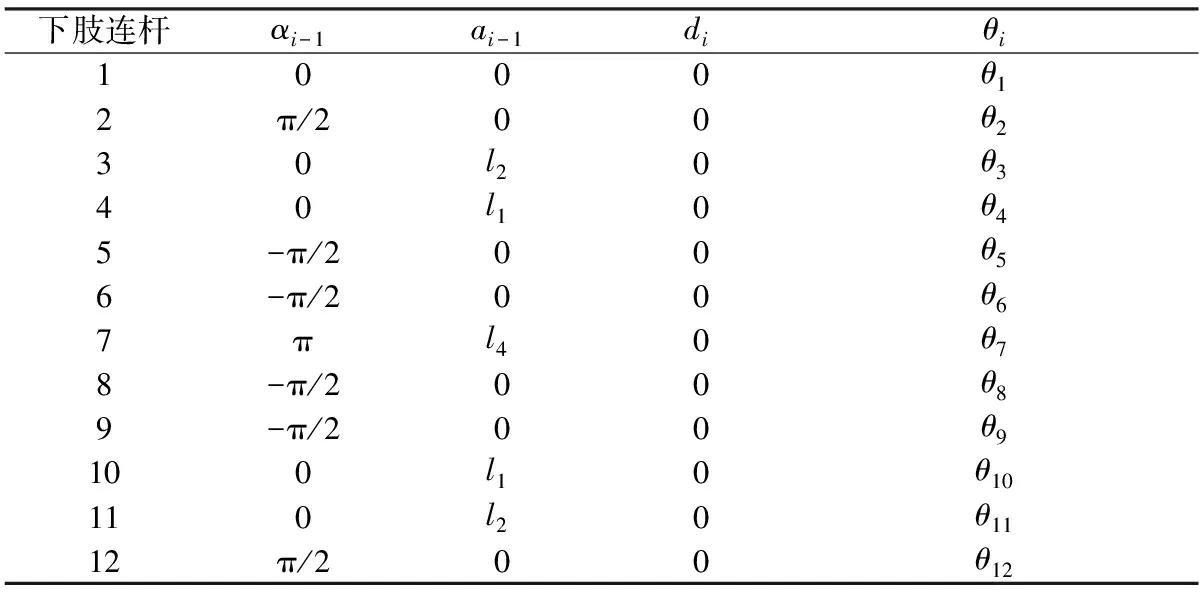
表 2 下肢D-H參數

建立運動學方程時，可將兩腿分別視為兩個串聯機構。擺動腿相對于支撐腿的運動可以視為腰部坐標系{W}相對于支撐腿運動和擺動腿相對于腰部坐標系{W}運動的疊加，這樣可簡化計算過程。

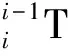
(1)

腰部坐標系{W}到基坐標系{0}的變換矩陣如式(2)所示：

(2)

坐標系{12}到坐標系{W}的變換矩陣如式(3)所示：

(3)

2.2.2 逆運動學分析

由圖2(a)所示的人體下肢結構可知，當膝關節轉角不為零時，無論腿部怎么運動，A、B、C三個點都構成一個三角形，且B點處的轉角θ3的取值范圍在[-π/2,0]之間。為此，采用解析幾何法進行逆運動學分析[14]。

由正運動學分析可知，坐標系{6}到基坐標系{0}的變換矩陣如式(4)所示：

(4)

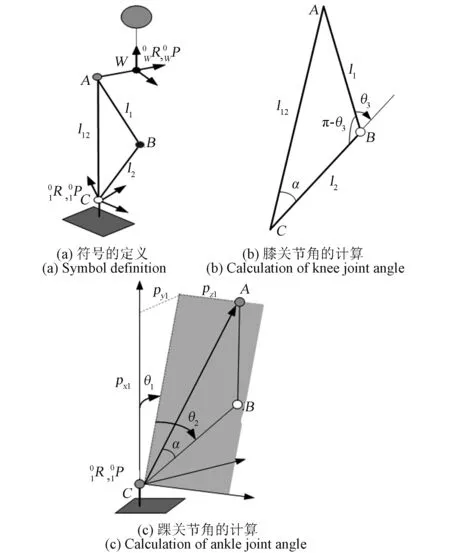
圖2 逆運動學分析方法Fig.2 Inverse kinematics analysis method

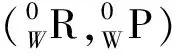
(5)

參考圖2(b)可得，膝關節角度如式(6)：

(6)

在踝關節坐標系下，如圖2(c)所示，根據l12可以求得踝關節的俯仰角和滾動角分別為式(7)、式(8)：

θ1=atan2(py1,px1)

(7)

(8)

式中，atan2(y,x)是用來求xy平面上的矢量(x,y)與x軸之間夾角的函數。sign(x)為符號函數，當x為正時取值為+1，x為負時取值為-1。

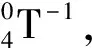
(9)

令公式(9)兩邊矩陣對應元素相等可求得式(10)～(13)：

θ234=atan2(r33,-(cosθ1r13+sinθ1r23))

(10)

θ4=θ234-θ2-θ3

(11)

θ5=atan2(sinθ5,cosθ5)

(12)

θ6=atan2(sinθ6,cosθ6)

(13)

3 航天服-航天員下肢系統動力學分析

星表出艙作業時，航天員著艙外航天服后需具有行走移動的能力。為了分析充壓航天服對航天員直立行走過程中運動能力的影響，下面將對人服下肢系統的步態行走進行動力學建模與分析。

3.1 動力學建模

在前文完成的12個自由度的下肢系統正逆運動學分析的基礎上，可以進行航天員-航天服系統的動力學分析，但求解十分繁瑣和復雜。考慮到步態行走主要是矢狀面內的運動，因此本文僅研究矢狀面內的下肢運動。直立行走過程中，航天員的下肢運動姿態可劃分為擺動相和支撐相。下面利用拉格朗日方程法分別對航天員的擺動相和支撐相進行動力學建模與分析。

3.1.1 擺動相動力學建模

下肢單腿擺動模型如圖3所示，在此種運動模式下，髖關節與上軀干固定，模型簡化為頂端固定的三連桿。

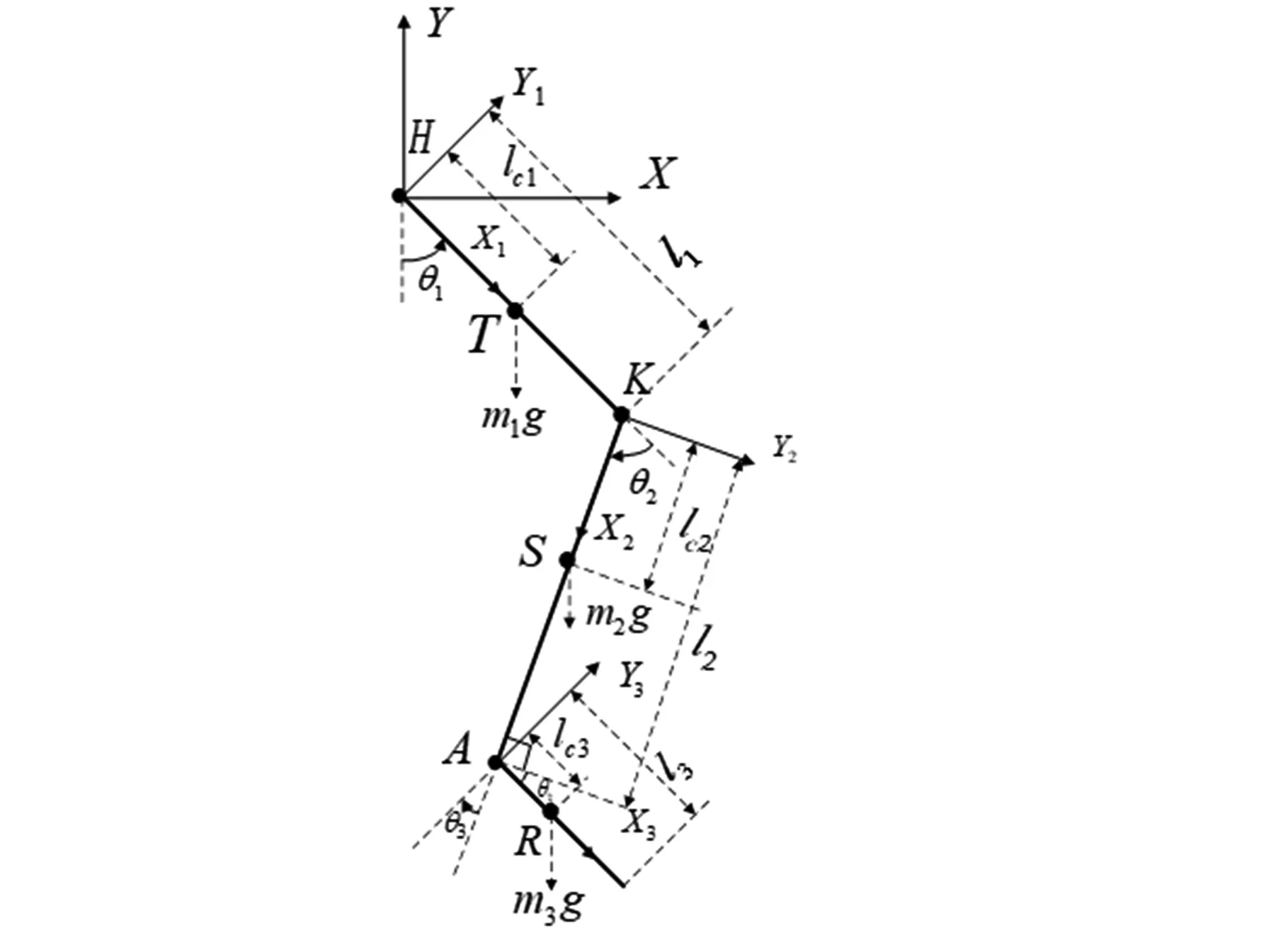
圖3 擺動相模型Fig.3 Swing phase model

圖3中：H、K和A分別表示髖關節、膝關節和踝關節；髖關節、膝關節和踝關節對應的角度分別為θ1、θ2和θ3，力矩分別是Mh、Mk和Ma，大腿和小腿及腳的質量分別為m1、m2和m3，長度分別為l1、l2和l3，質心分別位于T、S和R處，離關節中心的距離分別為lc1、lc2和lc3。

以XY為世界坐標系，則各桿件的質心(Xi,Yi)依次為式(14)～(16)：

(14)

(15)

(16)

則下肢單腿的動能如式(17)所示：

(17)

其中，Ii為各桿件繞其質心的轉動慣量，φ1=θ1，φ2=θ1+θ2，φ3=θ1+θ2+θ3。

以X軸所在平面為零勢能面，下肢單腿的勢能如式(18)所示：

(18)

Lagrange函數L如式(19)所示：

L=K-P

(19)

Lagrange動力學方程如式(20)所示：

(20)

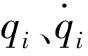
3.1.2 支撐相動力學建模

當人體下肢處于支撐相時，忽略腳底對踝關節位置的影響，同時忽略踝關節與地面接觸，可以將模型簡化為底端固定的三連桿模型，如圖4所示。

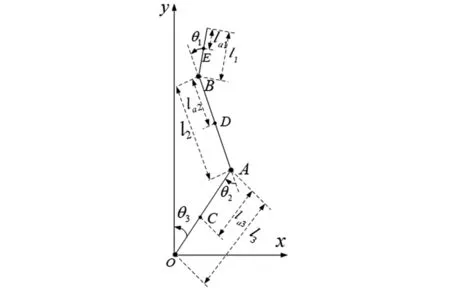
圖4 支撐相模型Fig.4 Stance phase model

圖4中：mi為各桿件質量，其中i=1,2,3；li為各桿件長度；lai為桿件質心距兩桿交點的距離；θi為桿件間的夾角；B、A和O分別表示髖關節、膝關節和踝關節，髖關節、膝關節和踝關節對應的角度分別為θ1、θ2和θ3；軀干、大腿和小腿的質量分別為m1、m2和m3，長度分別為l1、l2和l3，質心分別位于E、D和C處，離關節中心的距離分別為la1、la2和la3。

以xy為世界坐標系，則各桿件的質心(xi,yi)依次如式(21)～(23)所示：

(21)

(22)

(23)

以x軸所在的平面為零勢能面，Lagrange函數L如式(24)所示：

(24)

其中，φ1=θ1+θ2+θ3，φ2=θ2+θ3，φ3=θ3。

后續的動力學計算過程與擺動相類似，不再贅述。特別地，如圖4所示的支撐相有兩種情況：單腿支撐和雙腿支撐。雙腿支撐時，可將下肢模型分為左腿支撐和右腿支撐模型，兩種模型的動力學模型計算方法類似，只是軀干處的質量和質心位置有所不同。

3.1.3 動力學分析

月球上的低重力環境使得航天員在月球上的步態行走與地球上存在一定的差異，但由于航天員在月表行走的下肢各關節步態數據難以獲取，本文擬使用臨床步態分析數據CGA(Clinical Gait Analysis)[15]作為航天員步態行走運動曲線，進行后續的動力學分析。定義一個步態周期為1 s，下肢各關節角度的定義如圖5所示。以逆時針方向為正方向，髖關節角為垂直軸到大腿中心線的角度，即θhip；膝關節角為大腿中心線到小腿中心線的角度，即θknee；踝關節角為小腿中心線到腳底平面法線的角度，即θankle。各關節角度曲線如圖6所示。

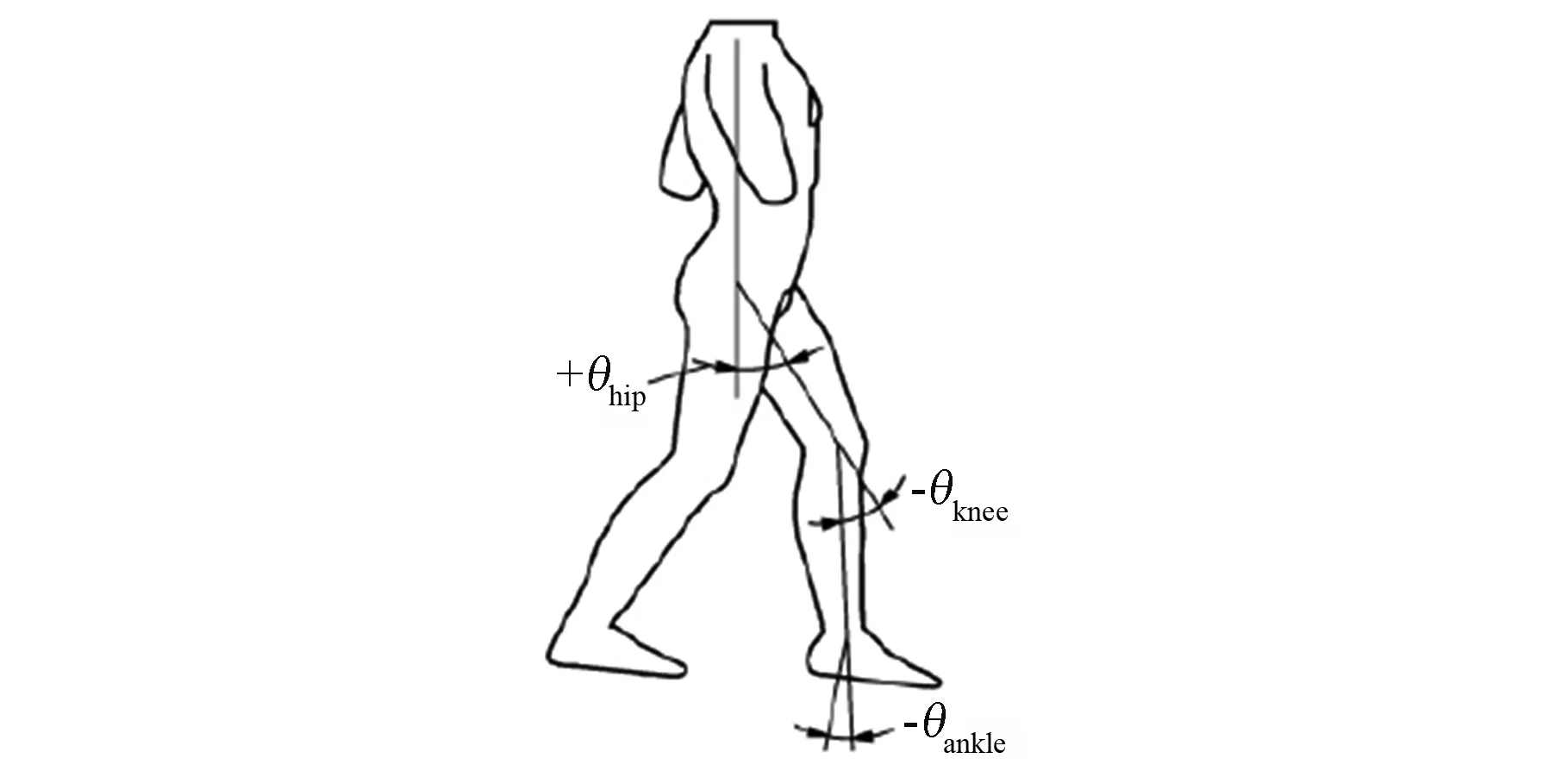
圖5 人體步態數據定義Fig.5 Definition of huma gait data

圖6 關節角度曲線Fig.6 Joint angle curves

將表1所列航天員肢體物理參數及CGA步態數據曲線分段(前60%為支撐相曲線，后40%為擺動相曲線)代入支撐相和擺動相動力學模型中，可得到航天員一個步態周期內髖關節、膝關節和踝關節關節力矩變化曲線，如圖7所示。可以看到，髖關節所受力矩最大，在支撐相末期達到最大力矩，隨后進入擺動相，關節力矩減小。膝關節的正負力矩極值近似，而踝關節的關節力矩波動最小。

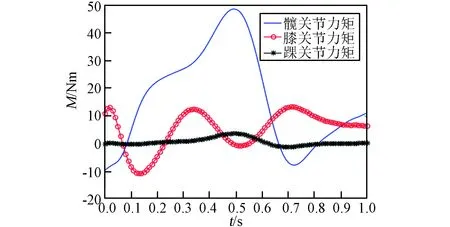
圖7 關節力矩曲線Fig.7 Torque curve of joints

3.2 著服航天員下肢系統動力學分析

3.2.1 著服航天員直立行走關節力矩分析

航天服對航天員下肢系統的影響主要表現為質量、慣量以及服裝阻力矩對關節力矩的影響。因此著服航天員下肢系統動力學模型由著服未充壓航天員下肢系統動力學模型和充壓關節阻力矩模型組成。 著服未充壓航天員下肢系統動力學模型可采用上節相同的方法建立，此處不再贅述。需要說明的是，拉格朗日函數L的推導過程中質量和慣量均為人服系統的總質量和總慣量。充壓EMU航天服下肢關節角度與力矩關系曲線采用文獻[16]提供的角度力矩遲滯曲線。圖8給出了一個步態周期內，關節阻力矩隨時間的變化曲線。

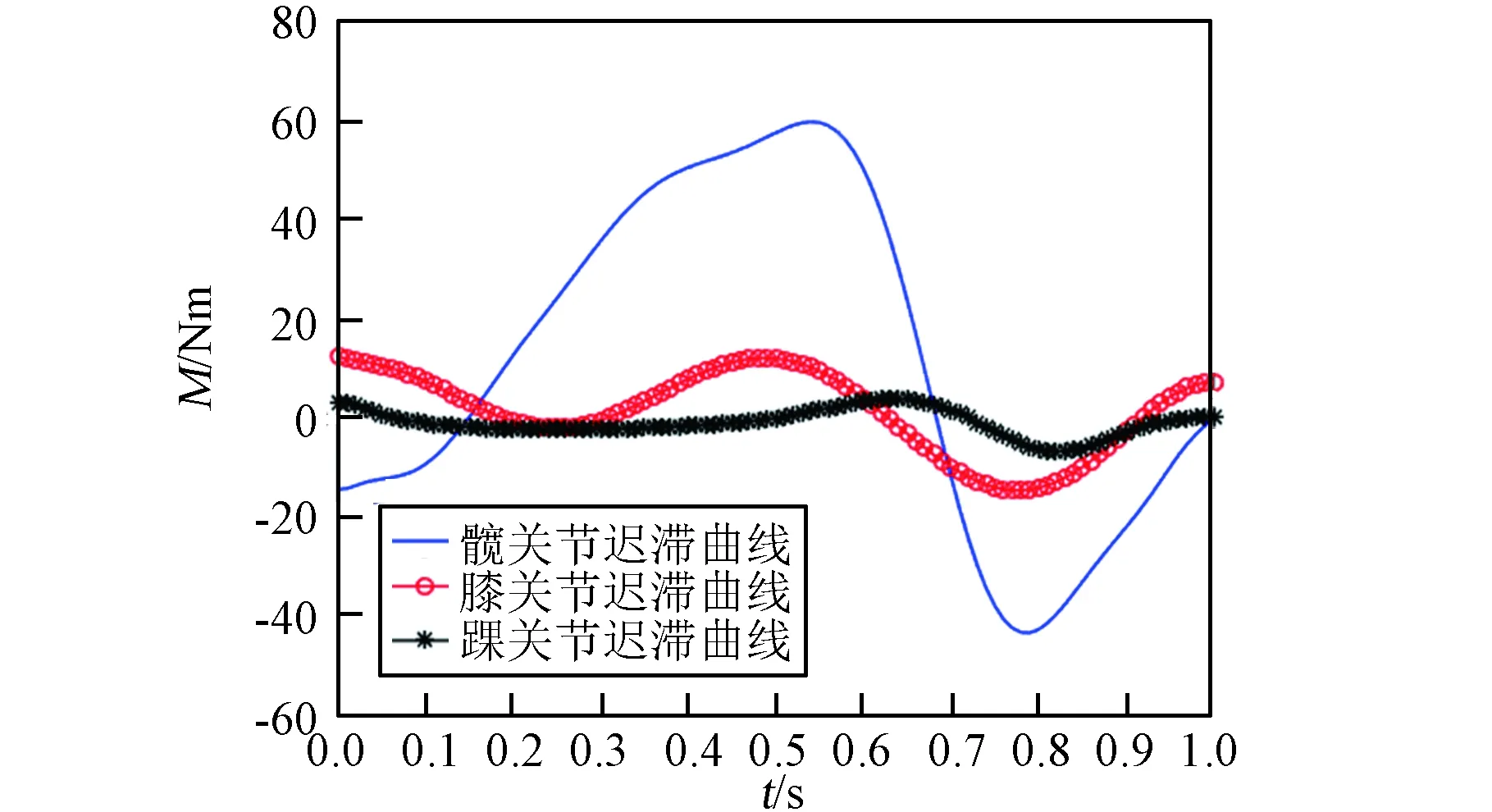
圖8 關節遲滯曲線Fig.8 Hysteresis curve of joints

圖9～圖11匯總了航天員未著服、著服未充壓以及著服充壓三種情況下，完成一個步態周期動作時航天員下肢各關節的關節力矩。

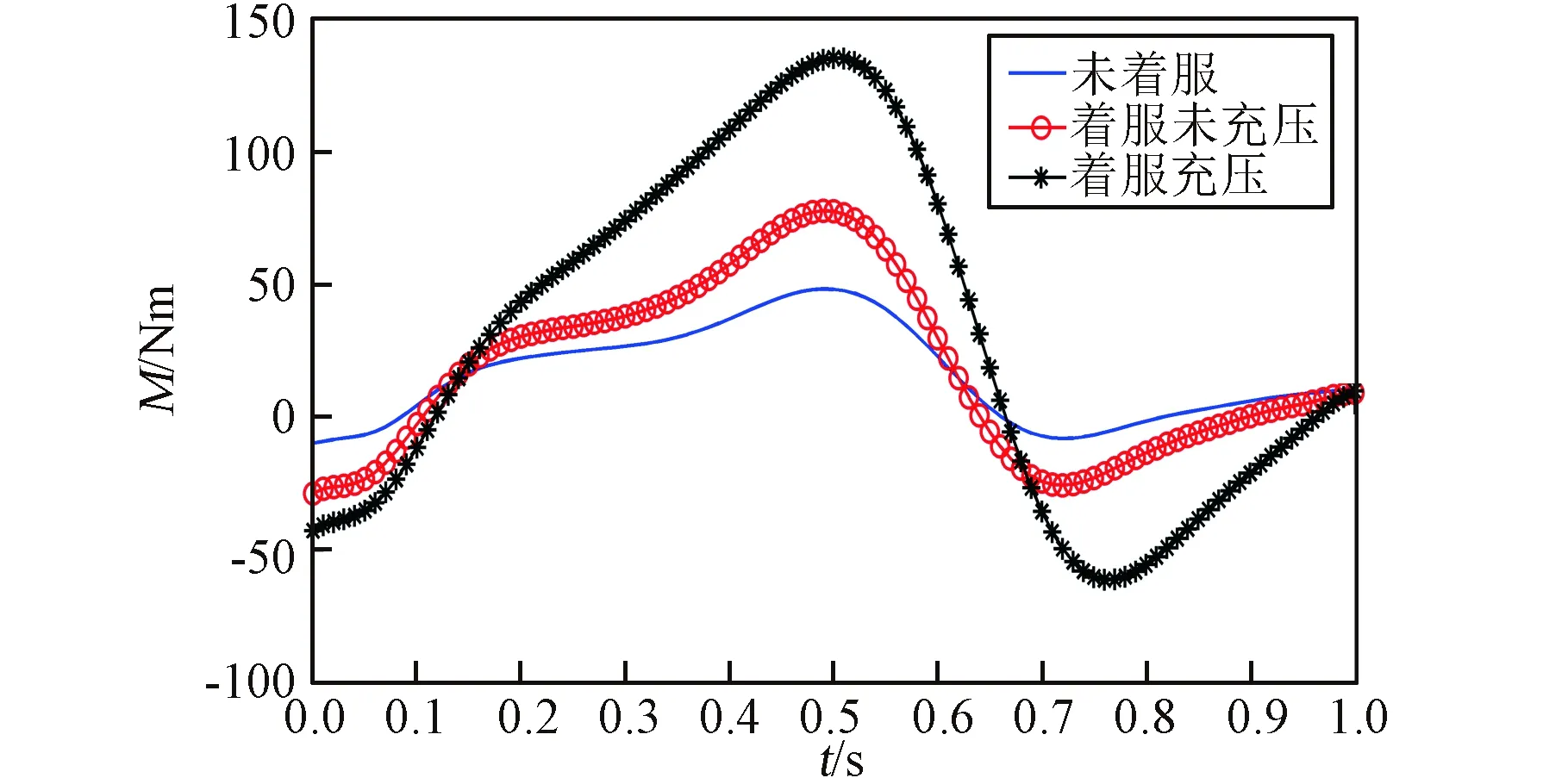
圖9 不同情況下髖關節力矩對比Fig.9 Comparison of hip torque under different conditions

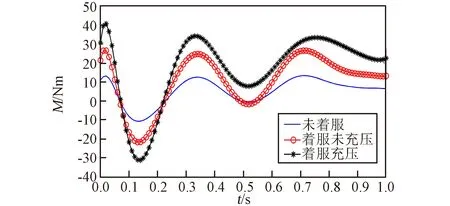
圖10 不同情況下膝關節力矩對比Fig.10 Comparison of knee torque under different conditions

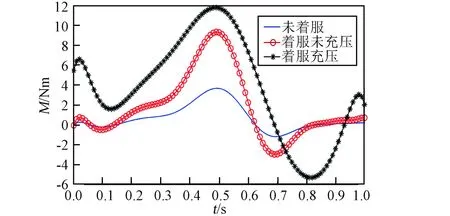
圖11 不同情況下踝關節力矩對比Fig.11 Comparison of ankle torque under different conditions

圖9～圖11所示曲線表明，當航天員在未著服、著服未充壓和著服充壓狀態下完成相同的直立行走運動，航天服質量、轉動慣量和服裝關節阻力矩導致人體下肢各關節的關節力矩明顯增加。對比各關節著服充壓與未著服的力矩變化，髖關節力矩增加幅度為[-40，90]N·m，膝關節力矩增加幅度為[-15，25] N·m，踝關節力矩增加幅度為[-4，8] N·m。

航天員在一個步態周期內，當下肢各關節按照CGA時間角度曲線運動時，各個關節所做的功可以通過表達式(25)計算：

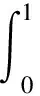
(25)

式中，M表示關節力矩，ω表示關節角速度。通過計算，航天員在未著服和著服狀態下的下肢各關節在一個步態周期內的總功列入表3。

表 3 未著服與著服時關節總功值

由表3可以看出，在一個步態周期內，著服航天員髖關節、膝關節和踝關節所做的功比未著服時分別增加了205%、134%和95%。在這種情況下，航天服會增加航天員的能量消耗，肌肉的疲勞會比預期更快。

3.2.2 不同路況下著服航天員關節力矩分析

航天員在月面開展出艙作業時，因月面崎嶇不平或探測任務需求，將在上下坡、上下樓梯或平地等路況下行走。有研究表明，人體步態在不同路面狀況下表現出不同的特征，如不同路況下支撐期和擺動期在整個步態周期內所占的比例不同，髖、膝和踝關節所需力矩不同，其中支撐期差別最為明顯[17]。文獻[18]和[19]分析了行走、上下樓梯過程中下肢關節角度的變化。

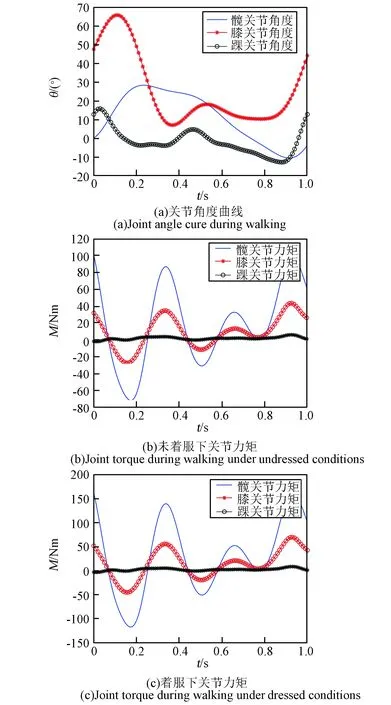
圖12 正常步態力矩對比Fig.12 Comparison of torque in normal gait

依據前文建立的動力學模型，參考文獻[19]在正常行走、上下臺階給出的下肢關節在矢狀面內的運動角度時間曲線，圖12、圖13和圖14分別給出了未著服和著服未充壓狀態下航天員正常行走、上下臺階時下肢關節角度和力矩變化曲線。由于上下樓梯關節角度變化較大，角度限值超過文獻[16]所示的充壓航天服關節遲滯曲線中的角度值，因此，本文僅分析了航天服質量和慣性對關節力矩的影響。

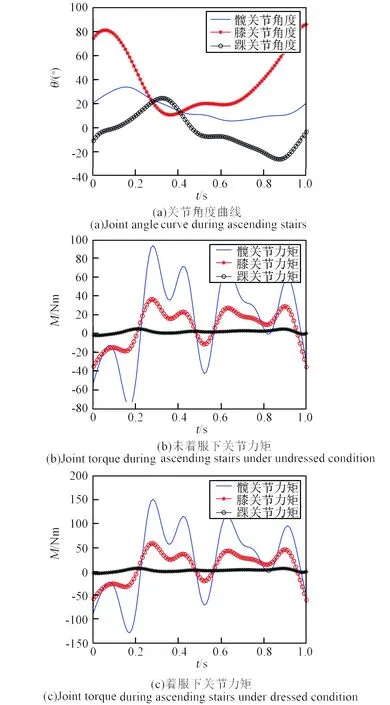
圖14 下樓梯力矩對比Fig.14 Comparison of torque during descending stairs

從圖12～14可以看出，上下樓梯過程中髖關節和膝關節的角度變化范圍大于正常行走的角度變化，因此，在未著服和著服狀態下，髖關節和膝關節處關節力矩極值均大于行走過程中相應極值。以上樓梯為例，未著服情況下，髖關節力矩變化范圍為[-47.0, 129.9]N·m，而著服狀態下，髖關節力矩變化范圍為[-75.3, 204.3]N·m；膝關節力矩變化范圍由未著服狀態下的[-30.6, 50.2]N·m變為著服狀態下的[-48.4, 82.4] N·m。可以看到，航天服質量和慣性的存在使得著服航天員需要消耗更多的能量來完成相應的動作，從而影響航天員的工作效率。

4 結論

1)正常步態行走過程中，艙外航天服的質量、慣性和關節阻力矩增加了航天員下肢關節的運動負荷，而且髖關節受到的影響最大。

2)不同的路況下行走時，髖關節、膝關節和踝關節的步態特征不同，艙外航天服對各個關節的影響不同。

因此，綜合分析不同路況下航天服對著服航天員運動負荷的影響，合理確定航天服質量、航天服關節結構形式，降低航天服對航天員活動性和操作能力的影響是非常必要的。本文在進行航天服-航天員系統動力學建模時，認為人服的關節位置完全重合，將人體下肢各節段假設為剛體，而將航天服作為人體模型的附加質量和慣性進行考慮，步態分析數據也基于地面步態測量，未考慮低重力環境對步態引起的差異。這些方面都需要進一步探討，后續可在OpenSim軟件平臺下，建立人體骨肌模型模擬人體的真實的生理結構，同時引入航天服屬性，通過人服耦合的動力學分析，評估航天員訓練及出艙活動中的體力負荷和骨肌風險，同時考慮星表低重力步態情況，為航天服設計提供一定參考。