交流電力測功機運行狀態的混沌預測與異常診斷

鐘定清，王艾倫，何謙，魏克湘

?

交流電力測功機運行狀態的混沌預測與異常診斷

鐘定清1, 2，王艾倫1，何謙1，魏克湘2

(1. 中南大學 機電工程學院，湖南 長沙，410083；2. 湖南工程學院 機械工程學院，湖南 湘潭，411104)

為提高交流電力測功機運行過程的安全性與可靠性，利用混沌理論對交流電力測功機運行狀態的特征信息進行混沌辨析，主要內容包括對交流電力測功機運行過程中的齒輪最大溫度、繞組最大溫度、轉速、有功功率進行混沌預測，對交流電力測功機運行過程中的油膜渦動、流體激勵、徑向碰摩狀態進行混沌診斷。研究結果表明：運行狀態參數齒輪最大溫度、繞組最大溫度和轉子平均轉速混沌預測的平均相對誤差均為8.75%；通過混沌關聯維數可以較好地區分交流電力測功機的油膜渦動異常、流體激勵異常和碰摩異常這3種異常運行狀態，為交流電力測功機的運行狀態檢測提供一種新思路。

交流電力測功機；運行狀態檢測；混沌預測；混沌診斷

測功機是動力傳動系統試驗臺(包括發動機以及電機性能測試平臺等)中的核心裝置。傳統的水力測功機、機械摩擦測功機以及電渦流測功機都會在工作過程中產生大量的熱量并耗散，造成能量浪費，而且需在測功機系統中配置散熱裝置。與傳統測功機相比，交流電力測功機在實現機械功率測量功能的同時，還可以實現能量回收，因此，交流電力測功機的應用日趨普遍[1]。交流電力測功機的運行狀態檢測在交流電力測功機管理與維修中具有重要地位，對提高交流電力測功機工作效率和可靠性、高效性、可維修性和經濟性等方面起著極其重要的作用。交流電力測功機的運行狀態檢測是通過測量反映其運行特征的參數信號并提取其征兆信息來預測和判定運行狀態[2]。但實際測量得到的部分運行特征參數信號是不規則的，這些特征信號在一定尺度范圍內都具有混沌特征，因此，將混沌理論引入測功機運行狀態異常診斷領域，從那些不規則的信號中找出其信息特征，借助于混沌理論可對運行狀態的特征信號進行預測和異常診斷[3]。在非線性預測方法中，混沌理論是一個重要的研究方向，混沌時間序列的預測近年來引起了人們的廣泛關 注[4]，目前常用的預測模型主要有自回歸滑動平均混合模型、灰色預測模型、神經網絡預測模型等。其中，自回歸滑動平均混合模型不能反映事物的內在聯系，多項式中系數的選擇對預測精度影響較大，僅適用于短期預測[5]；灰色預測模型能夠對中長期時間序列進行預測，但對時間序列具有較強波動性的預測誤差較大[6]；神經網絡預測模型雖然預測精度高，但屬于黑箱模型，無法對模型輸入與輸出關系進行數學表達，且預測運算收斂速度較慢[7?8]。為此，AN等[9?13]提出了多種利用不同非線性函數的改進方法，促進了混沌時間序列預測的發展。目前，利用混沌特征檢測噪聲背景中的系統運行狀態特征信息成了系統運行狀態判定的研究熱點，如：DLASK等[14]利用混沌理論對旋轉頻譜信號進行分析，結果顯示不同故障信號具有明顯不同的關聯維數；SRIRAAM[15]提出了一種利用關聯維數的腦電信號無損壓縮處理后預測的神經網絡預測器；張英堂等[16]采用混沌理論分析了柴油機缸蓋振動信號，結果顯示當氣門處于不同狀態時，柴油機缸蓋振動信號的多重分形維數譜是不同的，可以作為判斷氣門狀態的依據。本文作者基于混沌理論的運行狀態預測與診斷技術，將該方法用于交流電力測功機運行狀態檢測。

1 混沌特征參數

1.1 相空間重構

時間序列的相空間重構主要是坐標延遲重構，其本質是通過一維的時間序列X的不同延遲時間構建維相空間矢量[17]：

嵌入維數和延遲時間是相空間重構的2個關鍵參數，嵌入維數和延遲時間的選取直接關系到系統動力學行為的恢復程度。

1.2 最佳延遲時間τ的選取

從理論上說，當數據點數無限多時，嵌入的效果與延遲時間無關，但當數據點數有限時，延遲時間對實際重構的影響極大[18]：若延遲時間太小，則吸引子不能充分展開，冗余誤差大；若延遲時間太大，則不相關誤差大，使得重構吸引子十分復雜。本文選取最佳延遲時間的選擇方法為互信息法。

假設有()和() 2個信息系統，()和()的概率密度分別為P[()]和P[()]，()和()的聯合概率為P[(),()]，則()與)的交互信息為

式中：()和()分別為()和()這2個信息系統的信息熵，信息熵越大，不確定性越強；(,)為聯合信息熵；P為聯合分布概率。交互信息函數(,)反映了和這2個信息系統間的相關性，若(,)越小，則和這2個信息系統間的相關性越弱，從而導致系統不確定。一般將交互信息曲線第1次下降到極小值所對應的延遲時間定為最佳延時時間。

1.3 最佳嵌入維數m的選取

為了確定嵌入維數，實際應用中通常的方法是計算吸引子的某些幾何不變量(如關聯維數、Lyapunov指數等)。選擇延遲時間后逐漸增加維數, 直到它們停止變化為止。分析Takens嵌入定理可知，這些幾何不變量具有吸引子的幾何性質，當維數大于最小嵌入維數時，幾何結構已被完全打開，此時，這些幾何不變量與嵌入的維數無關。基于此理論，可以選擇吸引子的幾何不變量停止變化時的嵌入維數作為重構的相空間維數[19]。

對于時間序列{1，2，…，x}，確定延遲時間后，嵌入維數設置為，則時間序列{1，2，…，x}相空間重構后的向量()為

當嵌入維數為+1時，時間序列{1，2，…，x}相空間重構后的向量(1)為

定義

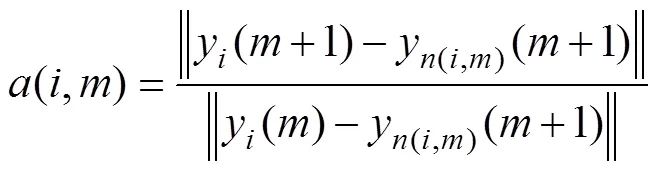
式中：(，)為在[1,?]區間內的正整數。

定義

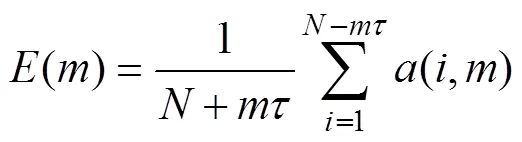
增大，當1()不再變化或者變化很小時，1便為最佳嵌入維數。

1.4 關聯維數和Lypaunov指數

交流電力測功機特征參數信號是否具有混沌特性，需要進行混沌判定。最常用的混沌判定方法是通過計算混沌信號奇異吸引子的特性參數來辨別混沌特性。常用描述奇異吸引子的特性參數指標包括最大關聯維數、Lypaunov指數[20]。

1)關聯維數。動力系統的關聯維數若為正分數，則判定它具有混沌特性。GRASSBERGER和PROCACCIA于1983年提出從一維時間序列中計算吸引子關聯維數的G?P算法[21]。

定義時間序列中重構相空間中兩向量的距離為

當向量間的距離小于時，稱為關聯向量，它們的關聯積分(,)為

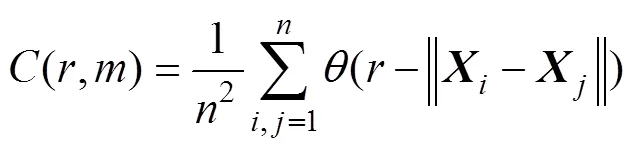
式中：

關聯維數與關聯積分(，)滿足對數線性關系，即

將式(11)兩端取對數后，可得

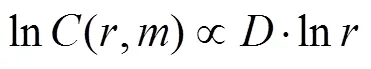
從式(12)可見：ln(,)與ln()間的線性關系斜率即為嵌入維數的關聯維數估計()。增大嵌入維數，重復上述步驟，直到相應的維數估計值()不再隨著的增大而在一定誤差范圍內不變為止。

2)Lyapunov指數。混沌系統對初始值極其敏感，2個相差很小的初始值會隨著時間的推移，軌跡按照指數方式分離。Lyapunov指數可定量描述該現象。Lyapunov指數表征系統在相空間中相鄰軌道間的收斂或發散程度，是衡量系統動力學特性的1個重要指標。Lyapunov指數為正，意味著混沌，也就是說，Lyapunov指數的重要作用之一就是判斷系統的混沌行為。

目前，常用的計算混沌序列最大Lyapunov指數的方法主要有以下幾種：由定義法延伸的Nicolis方法、Jacobian方法、Wolf方法、P-范數方法、小數據量方法。其中，以Wolf方法應用最廣泛，也最普遍。最大Lyapunov指數為

式中：為時刻時點與其距離最短的點0之間的距離。

2 交流電力測功機運行狀態混沌 預測

2.1 混沌預測模型

若交流電力測功機運行狀態具有混沌特征，則可充分利用交流電力測功機運行狀態參數的混沌特性對其進行趨勢預測。混沌預測方法可分為全局法和局域法。本文應用加權一階局域法預測模型對交流電力測功機運行狀態進行預測，其具體步驟如下。

1) 尋找臨近點。在相空間計算各鄰域點到之間的空間距離，找出的參考向量集， d為點到的距離(=l，2，…，)，d為其中的最小值。定義點的權重為

2) 局部線性擬合。一階加權局域線性擬合為

當嵌入維數=1時，有

由加權最小二乘法

將式(17)分別對和求偏導，可得：

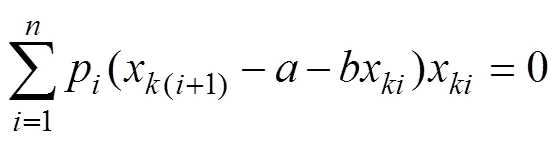
聯立式(18)和式(19)可得：

將式(20)和(21)代入式(15)，可求得的一步預測值+1。

2.2 實例分析

選取該交流電力測功機齒輪、繞組最大溫度、轉子平均轉速和有功功率這4個狀態特征參數作為研究對象。首先辨析交流電力測功機運行狀態的混沌特性，然后應用加權一階局部法，分別對相同時間段4個狀態參數進行趨勢預測。均取100個點數據(該序列每10 min采樣1點)。使用前70個點數據作為訓練樣本，對后30個點進行預測檢驗。

圖1所示為交流電力測功機的4個狀態特征參數(齒輪最大溫度、繞組最大溫度、轉子平均轉速和有功功率)的實測值與時間的關系。從圖1可以看出：交流電力測功機運行狀態參數時間序列具有較強的波動性，尤其對于轉子平均轉速和發電機有功功率，難以辨別交流電力測功機運行狀態參數的時間序列類型(如確定性時間序列、隨機序列或者混沌序列)，因此，需要重構相空間以判斷交流電力測功機運行狀態時間序列中是否具有混沌屬性。

取延遲時間為10~200 min，計算交流電力測功機齒輪最大溫度、繞組最大溫度、轉子平均轉速和有功功率狀態參數的交互信息函數值與延遲時間的關系，如圖2所示。從圖2可見：交流電力測功機齒輪最大溫度、繞組最大溫度、轉子平均轉速和有功功率等狀態參數交互信息函數值第1次達到極小值時的延遲時間分別為40，180，75和30 min。

應用式(5)~(7)計算得到1()與嵌入維數的關系如圖3所示。從圖3可以看出：當嵌入維數增加到6時，1()趨于穩定，因此，選交流電力測功機齒輪最大溫度時間序列的嵌入維數為6。同理可得交流電力測功機繞組最大溫度轉子平均轉速和有功功率時間序列的嵌入維數分別為7，6和10。

計算交流電力測功機運行狀態參數延遲時間和嵌入維數后，對其進行相空間重構，然后，應用式(13)計算交流電力測功機齒輪最大溫度、繞組最大溫度、轉子平均轉速和有功功率等狀態參數時間序列的最大Lyapunov指數max，如表1所示。

由表1可知：交流電力測功機齒輪最大溫度、繞組最大溫度、轉子平均轉速和有功功率等狀態參數時間序列的最大Lyapunov指數max分別為0.001 3，0.001 7，0.000 9和0.000 5，均大于0，表明交流電力測功機運行狀態具有明顯的混沌特性。

(a) 齒輪最大溫度；(b) 繞組最大溫度；(c) 轉子平均轉速；(d) 有功功率

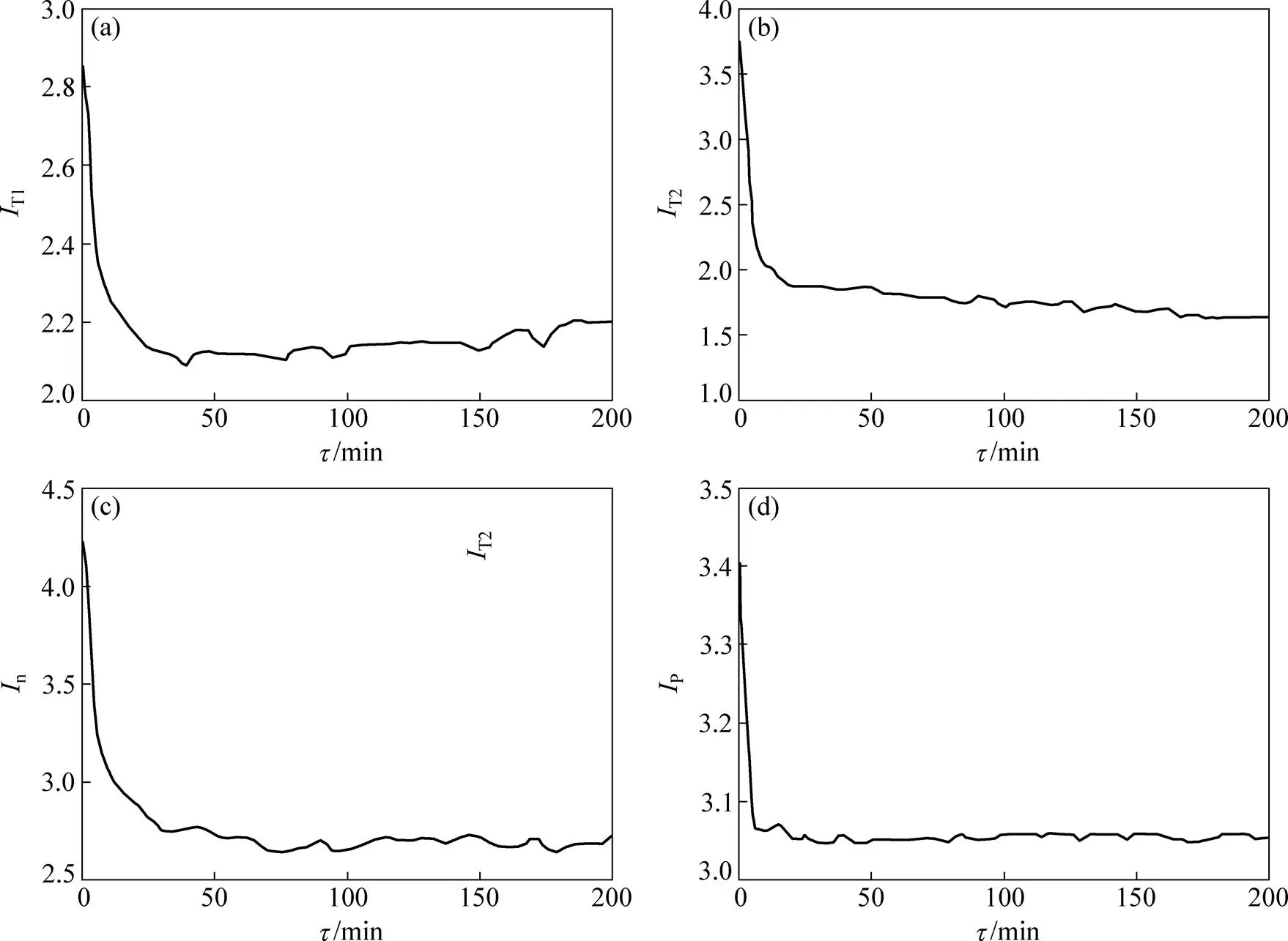
(a) 齒輪最大溫度交互信息函數IT1；(b) 繞組最大溫度交互信息函數IT2； (c) 轉子平均轉速交互信息函數In；(d) 有功功率交互信息函數IP

(a) 齒輪最大溫度運行狀態參數E1(m)1；(b) 繞組最大溫度運行狀態參數E1(m)2； (c) 轉子平均轉速運行狀態參數E1(m)3；(d) 有功功率運行狀態參數E1(m)4

表1 交流電力測功機運行狀態參數時間序列的最大Lyapunov指數

Table 1 The largest Lyapunov exponents of running state parameter time series for AC power dynamometer

應用加權一階局域法多步預測模型分別對交流電力測功機齒輪最大溫度、繞組最大溫度、轉子平均轉速和有功功率等運行狀態參數序列進行預測。用前70點數據進行相空間重構，用后30點數據進行預測，其預測結果如圖4所示。從圖4可見：交流電力測功機齒輪最大溫度、繞組最大溫度和轉子平均轉速等運行狀態參數預測平均相對誤差均為8.75%，具有較高精度，可滿足實際工作要求。交流電力測功機的有功功率的預測值和實際值比較接近，預測平均相對誤差為3.97%，預測精度較高。由于被測交流電力測功機轉速不穩定，導致轉子平均轉速時間序列變化幅度較大，預測出現了較大的偏差，預測平均相對誤差為10.97%。

3 交流電力測功機異常狀態混沌 分析

3.1 混沌判定模型

傳統的混沌G?P算法是目前工程上采用最 多的算法。然而，當分析信號處于異常時，該方 法存在很多限制，為此，本文提出一種改進的G?P算法。

原始G?P算法中，點間距按式(8)計算，為簡化運算，設點間距為

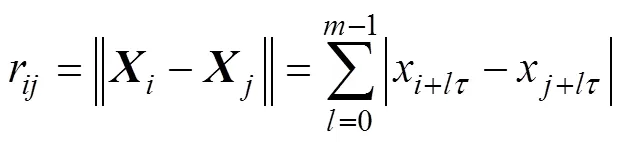
實際上，式(8)給出的是Rm球形域，而式(22)給出的分別是Rm菱形域，它們都是Rm凸集(其中，R為實數集)。采用式(8)計算點間距時，對每個m都要計算Nm(Nm?1)/2次，而采用式(22)計算時次數較少，其余的可按遞推公式

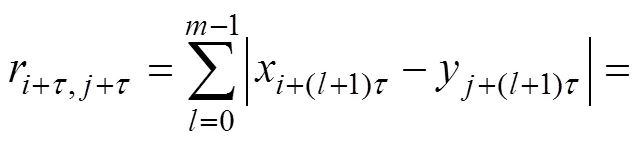
求得，這對于實時性要求較高的交流電力測功機運行狀態判定領域很有實用價值。

對所有的X(=1，2，…，N)重復上述過程，則可得所有的點間距。

3.2 實例分析

在交流電力測功測功機運行異常中，油膜渦動異常、流體激勵異常、碰摩異常的頻譜通常很接近，很難從頻譜圖上予以區分，如圖5和圖6所示。為此，應用混沌關聯維數對油膜渦動異常、流體激勵異常以及碰摩異常進行分析。

(a) 油膜渦動異常；(b) 流體激勵異常；(c) 碰摩異常

選取異常實例的數據長度為1 024點，嵌入維數從1到6變化，計算結果如圖7所示。

由圖7可見：以上交流電力測功機3異常信號的關聯積分在一定尺度范圍內不隨嵌入維數增加而增加，而是收斂到低維空間。通過對以上交流電力測功機3種異常的混沌進行計算，得到這些異常升速過程關聯維數變化范圍。分析結果表明：油膜渦動異常的關聯維數為1.0~1.2，流體激勵異常混沌吸引子的關聯維數范圍為1.3~1.5，而碰摩激勵異常的關聯維數為2.8~3.2，說明各自有不同的非線性產生機制，同時也說明關聯維數分析方法可將所有的異常能較好地 區分。

(a) 油膜渦動異常；(b) 流體激勵異常；(c) 碰摩異常

(a) 油膜渦動異常；(b) 流體激勵異常；(c) 碰摩異常

4 結論

1) 通過對交流電力測功機運行狀態參數時間序列進行非線性動力學建模，解析了交流電力測功機運行狀態的動力特征。交流電力測功機齒輪最大溫度、繞組最大溫度、轉子平均轉速和有功功率狀態參數時間序列的最大Lyapunov指數分別為0.001 3，0.001 7，0.000 9和0.000 5，均大于0，表明交流電力測功機運行狀態具有明顯的混沌特性。

2) 在對交流電力測功機運行狀態進行混沌預測時，應用加權一階局域預測方法，并采用某交流電力測功機實際運行數據對預測方法進行檢驗。交流電力測功機齒輪最大溫度、繞組最大溫度和轉子平均轉速等運行狀態參數預測平均相對誤差均為8.75%，具有較高精度，可滿足實際工作要求。交流電力測功機的有功功率的預測值和實際值比較接近，預測平均相對誤差為3.97%，預測精度較高。

3) 在對交流電力測功機異常狀態進行判定時，利用異常信號不同混沌關聯維數可反映不同異常的動力學產生機制不同的特點，并可通過混沌關聯維數較好地區分3種異常類型。

[1] 張志剛, 張桂香, 劉騰, 等. 電力測功機轉矩影響因素模糊灰色關聯分析[J]. 電子測量與儀器學報, 2012, 26(8): 693?698. ZHANG Zhigang, ZHANG Guixiang, LIU Teng, et al. Fuzzy grey relation analysis on torque influence factors of alternating current electrodynamometer[J]. Journal of Electronic Measurement and Instrument, 2012, 26(8): 693?698.

[2] 左光磊. 交流電力測功機特性參數降噪處理及其轉矩軟測量研究[D]. 長沙: 湖南大學機械與運載工程學院, 2015: 8?17. ZUO Guanglei. Denoising for parametric signals of AC dynamometer and soft measurement of its torque[D]. Changsha: Hunan University. College of Mechanical and Vehicle Engineering, 2015: 8?17.

[3] WARREN K, HAWKINS R C, SPROTT J C. Substance abuse as a dynamical disease: evidence and clinical implications of nonlinearity in a time series of daily alcohol consumption[J]. Addictive Behaviors, 2003(28): 369?374.

[4] E Jiaqaing, WANG Yaonan, MEI Chi, et al.Chaos behavior of crude copper composition time series from the copper convertor and its predicable time scale[J]. Nonlinear Analysis:Real World Applications, 2006, 7(4): 651?661.

[5] BATCHELOR R, ALIZADEH A, VISVIKIS I. Forecasting spot and forward prices in the international freight market[J]. International Journal of Forecasting, 2007, 23(1): 101?114.

[6] MAO M, CHIRWA E C. Application of grey model GM(1,1) to vehicle fatality risk estimation[J]. Technological Forecasting and Social Change, 2006, 75(5): 588?605.

[7] XIAO Gang, NI Mingjiang, CHI Yong, et al. Gasification characteristics of MSW and an ANN prediction model[J]. Waste Management, 2009, 29(1): 240?244.

[8] HAQUE M E, SUDHAKAR K V. ANN back-propagation prediction model for fracture toughness in microalloy steel[J]. International Journal of Fatigue, 2002, 24(9): 1003?1010.

[9] AN Xueli, JIANG Dongxiang, ZHAO Minghao, et al. Short-term prediction of wind power using EMD and chaotic theory[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(2): 1036?1042.

[10] E Jiaqiang, QIAN Cheng, LIU Teng, et al. Chaos analysis on the acceleration control signals of the piezoelectric actuators in the stewart platform[J]. Shock and Vibration, 2016, 2016: 1?9.

[11] E Jiaqiang, ZUO Qingsong, LIU Haili, et al. Endpoint forecasting on composite regeneration by coupling cerium-based additive and microwave for diesel particulate filter[J]. Journal of Central South University, 2016, 23(8): 2118?2128.

[12] E Jiaqiang, QIAN Cheng, LIU Haili, et al. Design of the H∞robust control for the piezoelectric actuator based on chaos optimization algorithm[J]. Aerospace Science and Technology, 2015, 47: 238?246.

[13] HAGHIGHI H S, MARKAZI A H D. Chaos prediction and control in MEMS resonators[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(10): 3091?3099.

[14] DLASK M, KUKAL J. Application of rotational spectrum for correlation dimension estimation[J]. Chaos, Solitons & Fractals, 2017, 99: 256?262.

[15] SRIRAAM N. Correlation dimension based lossless compression of EEG signals[J]. Biomedical Signal Processing and Control, 2012, 7(4): 379?388.

[16] 張英堂, 任國全, 李國璋.柴油機振動信號分形特征診斷的改進算法[J]. 內燃機學報, 2006, 24(5): 459?464. ZHANG Yingtang, REN Guoquan, LI Guozhang. Improved algorithm of diesel engine diagnosis based on fractal dimension of vibration signals[J]. Transactions of CSICE, 2006, 24(5): 459?464.

[17] LI Mengshan, HUANG Xingyuan, LIU Hesheng, et al.Prediction of gas solubility in polymers by back propagation artificial neural network based on self-adaptive particle swarm optimization algorithm and chaos theory[J]. Fluid Phase Equilibria, 2013, 356(25): 11?17.

[18] WU Jun, LU Jian, WANG Jiaquan. Application of chaos and fractal models to water quality time series prediction[J]. Environmental Modeling & Software, 2009, 24(5): 632?636.

[19] SUN Y, BABOVIC V, CHAN E S. Multi-step-ahead model error prediction using time-delay neural networks combined with chaos theory[J]. Journal of Hydrology, 2010, 395(1/2): 109?116.

[20] SUN Fenglan, GAO Lingxia, ZHU Wei, et al. Generalized exponential input-to-state stability of nonlinear systems with time delay[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 44: 352?359.

[21] WILLIAMS G. Chows theory tamed[M]. London: CRC Press, 2014: 1?20.

Chaos prediction and abnormality diagnosis of running state of AC electrical dynamometer

ZHONG Dingqing1, 2, WANG Ailun1, HE Qian1, WEI Kexiang2

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China; 2. School of Mechanical Engineering, Hunan Institute of Engineering, Xiangtan 411104, China)

In order to improve the safety and reliability of the running state of alternating current(AC) dynamometer, chaos theory was applied to analyze the abstracted characteristics signals from the running state of AC dynamometer. The study includes the chao prediction of the maximum temperature of gear and winding, rotate speed and active power, the chao diagnosis of oil whirling, flow excitation and radial collision friction of alternating current dynamometer. The results show that the average relative errors of chao prediction of running state parameters of gear and winding and rotate speed are all 8.75% and the abnormal state of alternating current dynamometer can be differentiated by chaotic correlation, which provides a new method for the detection of running state, including oil whirl, fluid vibration and impact-rub of alternating current dynamometer.

alternating current dynamometer; running state detection; chaos prediction; chaos diagnosis

10.11817/j.issn.1672?7207.2019.02.007

TH6

A

1672?7207(2019)02?0295?09

2018?06?10；

2018?08?21

國家自然科學基金資助項目(11772126)(Project(11772126) supported by the National Natural Science Foundation of China)

鐘定清，博士研究生，從事復雜機電裝備非線性振動與控制研究；E-mail：zhdiqi@126.com

(編輯 陳燦華)