圓鋼管UHPC短柱軸壓承載力與變形能力計算模型

王震，王景全, 2，劉桐旭，修洪亮

?

圓鋼管UHPC短柱軸壓承載力與變形能力計算模型

王震1，王景全1, 2，劉桐旭1，修洪亮1

(1. 東南大學 混凝土及預應力混凝土結構教育部重點實驗室，江蘇 南京，210096；2. 東南大學 國家預應力工程技術研究中心，江蘇 南京，210096)

根據力的平衡和變形協調，推導出鋼管折減系數和核心混凝土增強系數的解析表達式，研究圓鋼管約束對超高性能混凝土(UHPC)軸壓強度的增強作用和環向應力對圓鋼管軸壓強度的折減作用；建立圓鋼管UHPC短柱軸壓承載力計算模型，并與已有的規范方法進行比較；基于Mander模型，根據橫向約束等效原則，建立圓鋼管約束UHPC單軸受壓本構模型，并利用理想彈塑性模型建立能夠考慮環向應力影響的圓鋼管單軸受壓本構模型，實現對圓鋼管UHPC短柱軸壓受力全過程的模擬，并與試驗結果進行比較。研究結果表明：與規范方法相比，承載力模型能夠更好地兼顧計算精度和可靠度；利用變形能力計算模型得到的全過程荷載?位移曲線與試驗結果較吻合。

鋼管混凝土；超高性能混凝土；軸壓承載力；變形能力；變形協調

超高性能混凝土(ultra high performance concrete, UHPC)因具有較高的抗壓強度和彈模、可利用的抗拉強度、良好的變形能力以及耐腐蝕等優點，自問世以來便引起了人們的重視[1]。一方面，國內外研究者針對UHPC的制備和基本性能開展了大量研究[2?5]；另一方面，UHPC也已從實驗室研究走向工程應用[6]。迄今為止，世界上已經有100多座橋梁使用UHPC，日本的羽田機場則利用UHPC制作了20多萬m2的飛機跑道和停機坪[7]。此外，UHPC與圓鋼管組合而成的圓鋼管UHPC柱也開始應用于高層建筑中[7?8]。作為承壓構件，圓鋼管UHPC短柱的軸壓性能至關重要。吳炎海等[9?10]進行了圓鋼管UHPC短柱的軸壓試驗，給出了軸壓承載力回歸公式以及圓鋼管UHPC整體的單軸受壓應力和應變關系；田志敏等[11]通過試驗研究了圓鋼管UHPC短柱在軸壓作用下的受力變形機理與破壞特點；GULER等[12]通過試驗研究了鋼管強度和徑厚比對承載力和延性的影響，并對各國規范中的方法進行了評價；羅華等[13]通過試驗研究了加載方式的影響。綜上可知：當前針對圓鋼管UHPC短柱軸壓承載力和變形能力的研究多基于試驗，缺少相關的理論計算模型。現有的關于圓鋼管混凝土短柱軸壓承載力的計算方法主要分為2類：一類是將鋼管混凝土視為統一體，研究其組合性能[14?15]；另一類是將鋼管和核心混凝土分開研究。其中，第2類又分為2種：一種是不考慮兩者的相互作用，如美國ACI規范[16]；另一種是考慮兩者的相互作用，即考慮鋼管約束對核心混凝土抗壓強度的增強作用和鋼管環向應力對鋼管軸向承載力的削弱作用[17?20]。然而，已有研究表明[21]，相比于普通混凝土，UHPC具有較小的泊松比，側限壓力對UHPC抗壓強度的提高程度也更小[21]，因此，現有計算方法不能直接應用于圓鋼管UHPC短柱。此外，鋼管和核心混凝土的相互作用是由于核心混凝土橫向膨脹受到鋼管約束而產生的，兩者之間應滿足變形協調[22]，現有的計算方法對此也未有充分考慮。本文作者在現有的考慮鋼管和核心混凝土相互作用計算方法的基礎上，引入變形協調條件，并計入UHPC材料特性的影響；建立圓鋼管UHPC短柱軸壓承載力計算模型，并利用已有試驗結果對建議模型和美國ACI規 范[16]、歐洲EC4規范[20]以及我國CECS28：2012[23]中的方法進行評價；同時，利用已有的關于箍筋約束UHPC的研究成果，按照橫向約束等效原則，建立基于Mander模型的圓鋼管約束UHPC單軸受壓本構模型，結合考慮了鋼管環向應力折減作用的鋼材理想彈塑性模型，實現對圓鋼管UHPC短柱軸壓受力全過程荷載位移曲線的模擬，并將計算結果與試驗結果進行 比較。

1 圓鋼管UHPC短柱軸壓承載力計算模型

現有的考慮鋼管和核心混凝土相互作用的圓鋼管混凝土短柱軸壓承載力u的計算[17?20]公式如下：

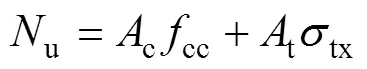
式中：c為核心混凝土面積；cc為圓鋼管約束UHPC的峰值應力；t為圓鋼管面積；tx為考慮環向應力折減后圓鋼管軸壓強度。

記c=cc/c(其中c為核心混凝土軸壓強度增強系數，c為UHPC圓柱體抗壓強度)，t=tx/y(其中t為鋼管軸壓強度折減系數，y為圓鋼管屈服強度)，則有

建議模型通過引入變形協調來考慮UHPC材性的影響，推導出關于圓鋼管UHPC短柱承載力計算所需的c和t這2個系數的解析公式。

1.1 基本假設

1) 圓鋼管UHPC短柱僅發生強度破壞，且破壞前鋼管和UHPC黏結良好，兩者之間無相對滑移。

2) 圓鋼管UHPC短柱僅承受軸壓荷載，柱子被均勻壓縮，并符合平截面假定，暫未計入偏心影響。

3) 核心UHPC各向同性，在達到極限受壓應力之前近似按彈性狀態分析。鋼管應力應變關系屈服前滿足線彈性，屈服后滿足米塞斯屈服(MISE)準則。

1.2 模型建立與公式推導

圓鋼管和核心UHPC的受力示意圖如圖1所示，其中為鋼管壁厚；為鋼管直徑；為鋼管與核心混凝土之間的徑向壓強；為沿軸向單位高度鋼管環向合力；c為核心混凝土直徑；tx為鋼管軸向應力；tθ為鋼管環向應力；tr為鋼管徑向應力；為鋼管軸向壓力。核心UHPC三向受壓，圓鋼管微元體可近似視為二向應力狀態。

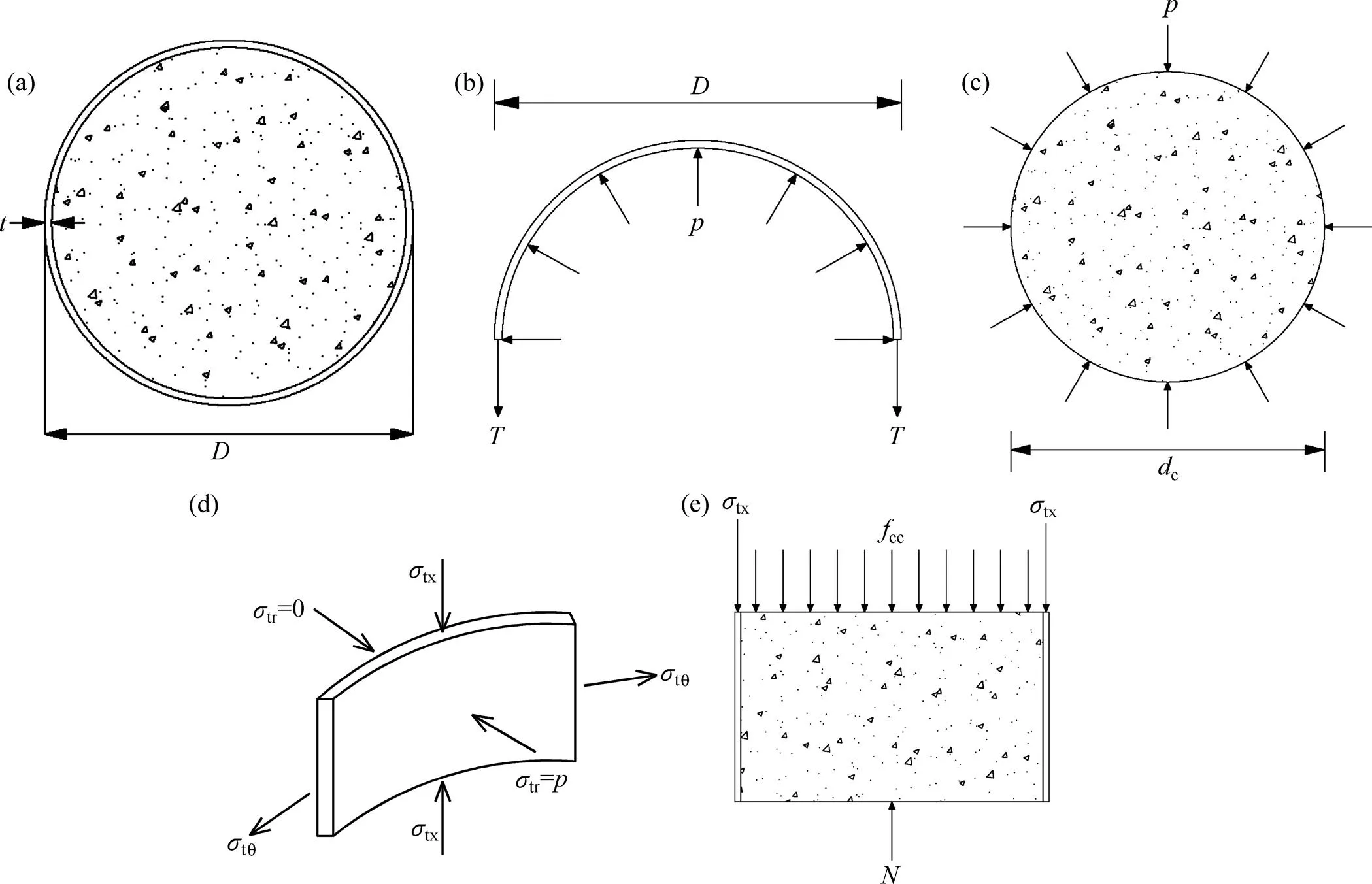
(a) 圓鋼管UHPC短柱截面直徑；(b) 鋼管截面內受力；(c) 核心UHPC截面內受力； (d) 鋼管單元體受力分析；(e) 圓鋼管UHPC短柱軸向受力分析

柱坐標系下核心UHPC的物理方程式如下：

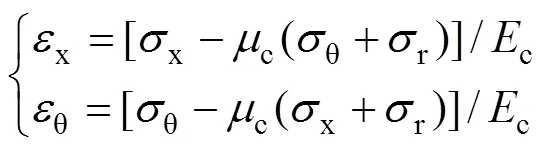
式中：c和c分別為核心UHPC的彈性模量和泊松比；x，θ和r分別為核心UHPC軸向應力、環向應力和徑向應力；x，θ和r分別為核心UHPC軸向應變、環向應變和徑向應變。

圓鋼管UHPC短柱在軸壓狀態下，可近似認為核心UHPC環向與徑向應力相等，即

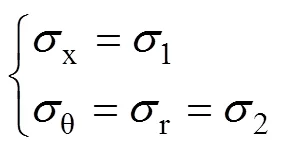
式中：1和2分別為核心UHPC軸向和橫向(水平向)主應力。

將式(4)代入式(3)可以得到

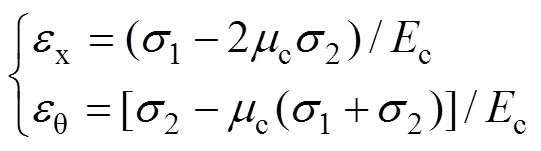
式(5)中以壓應力及應變為正值，拉應力及應變為負值，因此，x＞0，θ＜0，即核心UHPC軸向應變x為壓應變，環向應變θ為拉應變。為計算方便，在求解過程中保持θ為正值，即

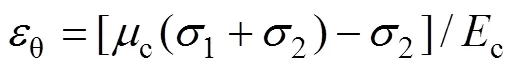
由圖1(d)可以得到鋼管軸向和環向應變表達式如下：

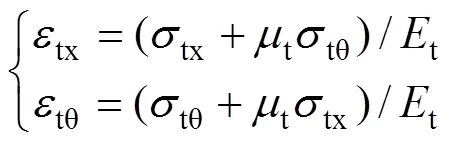
式中：tx和tθ分別為鋼管軸向和環向應變；t和t分別為鋼管的彈性模量和泊松比。

由變形協調可知：鋼管軸向應變tx等于核心UHPC軸向應變x，鋼管環向應變tθ等于核心UHPC環向應變θ，即

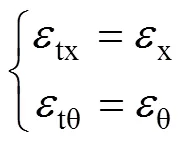
將式(5)~(7)代入式(8)，可以得到

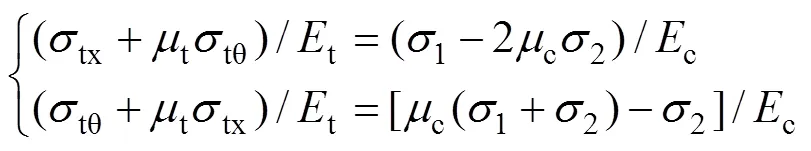
沿軸向單位高度鋼管環向應力tθ產生的合力與核心UHPC在軸壓荷載下產生的橫向外擴力相平衡(見圖1)，即

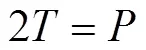
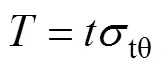
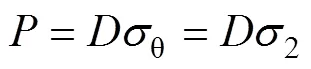
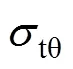
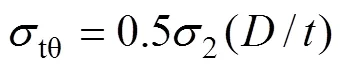
已知雙向側限混凝土軸向應力1與圓柱體抗壓強度c和側限應力2的關系式[18]如下：

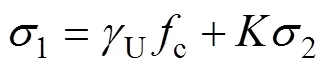
式中：為側限系數，對于普通混凝土，取值范圍為4.1~5.6[24]。已有研究表明，隨著側向壓力增大，UHPC抗壓強度增加幅度比普通混凝土的小[21]，故本文將UHPC的側限系數取為4.1；U為混凝土強度直徑折減系數，其計算公式如下：

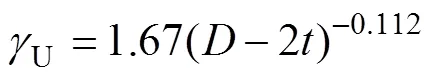
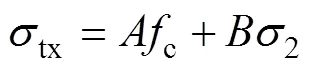
其中：

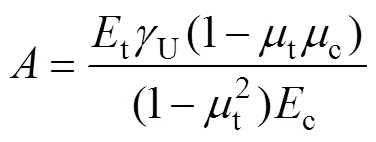
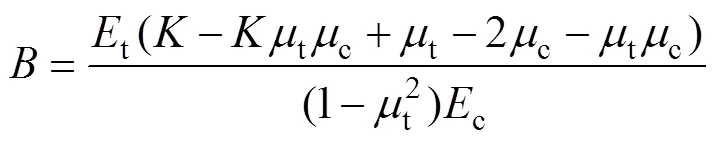
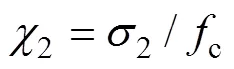
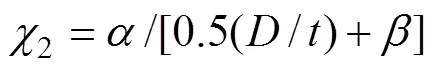
其中：

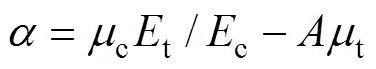
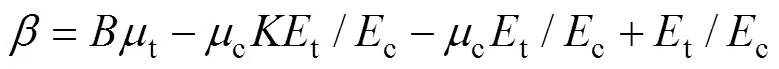
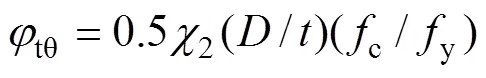
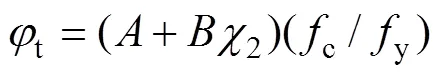
由式(23)計算得到t＞1，這對于屈服后滿足MISE準則的鋼管顯然是不合適的，因此，需要對式(23)進行修正。由鋼管應力滿足MISE準則可以得到

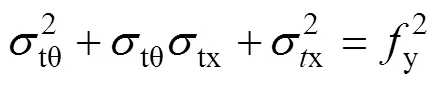
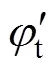
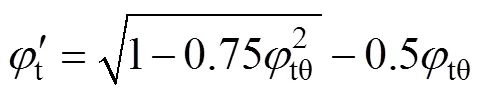
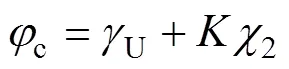
2 軸壓承載力計算模型試驗驗證及其與各國規范方法的比較

2.1 各國規范方法

歐洲的EC4規范[20]給出了圓鋼管混凝土柱軸壓承載力計算公式(見式(2))，其中鋼管混凝土柱截面有效剛度eff計算公式為

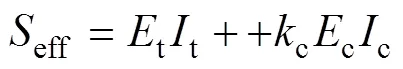
式中：t為鋼管的慣性矩；c為核心混凝土的慣性矩；c為考慮混凝土開裂的剛度折減系數，取0.6。

圓鋼管混凝土柱穩定承載力計算公式為

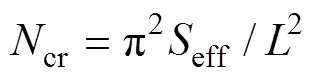
式中：為柱的計算長度。

圓鋼管混凝土柱的塑性承載力特征值pl,Rk為

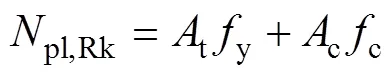
圓鋼管混凝土柱的相對長細比為

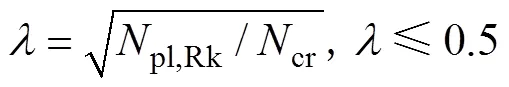
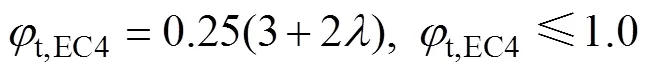
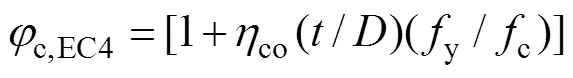
其中：

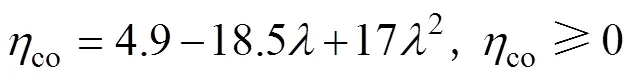
美國ACI規范[16]給出的圓鋼管混凝土短柱軸壓承載力計算公式則簡單得多，沒有考慮核心混凝土與鋼管的相互作用。

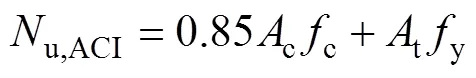
我國的CECS28:2012“鋼管混凝土結構設計與施工規程”[23]中規定的圓鋼管混凝土短柱軸壓承載力計算公式為

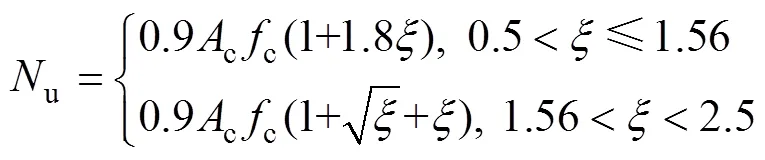
其中：=ty/(cc)。

2.2 試驗驗證

利用本文建議模型與各國規范方法對收集到的51根圓鋼管UHPC短柱試件的軸壓承載力進行計算，試件的具體參數見表1(其中，exp為軸壓承載力度驗值)，承載力計算值與試驗值對比分別見圖2和表2。

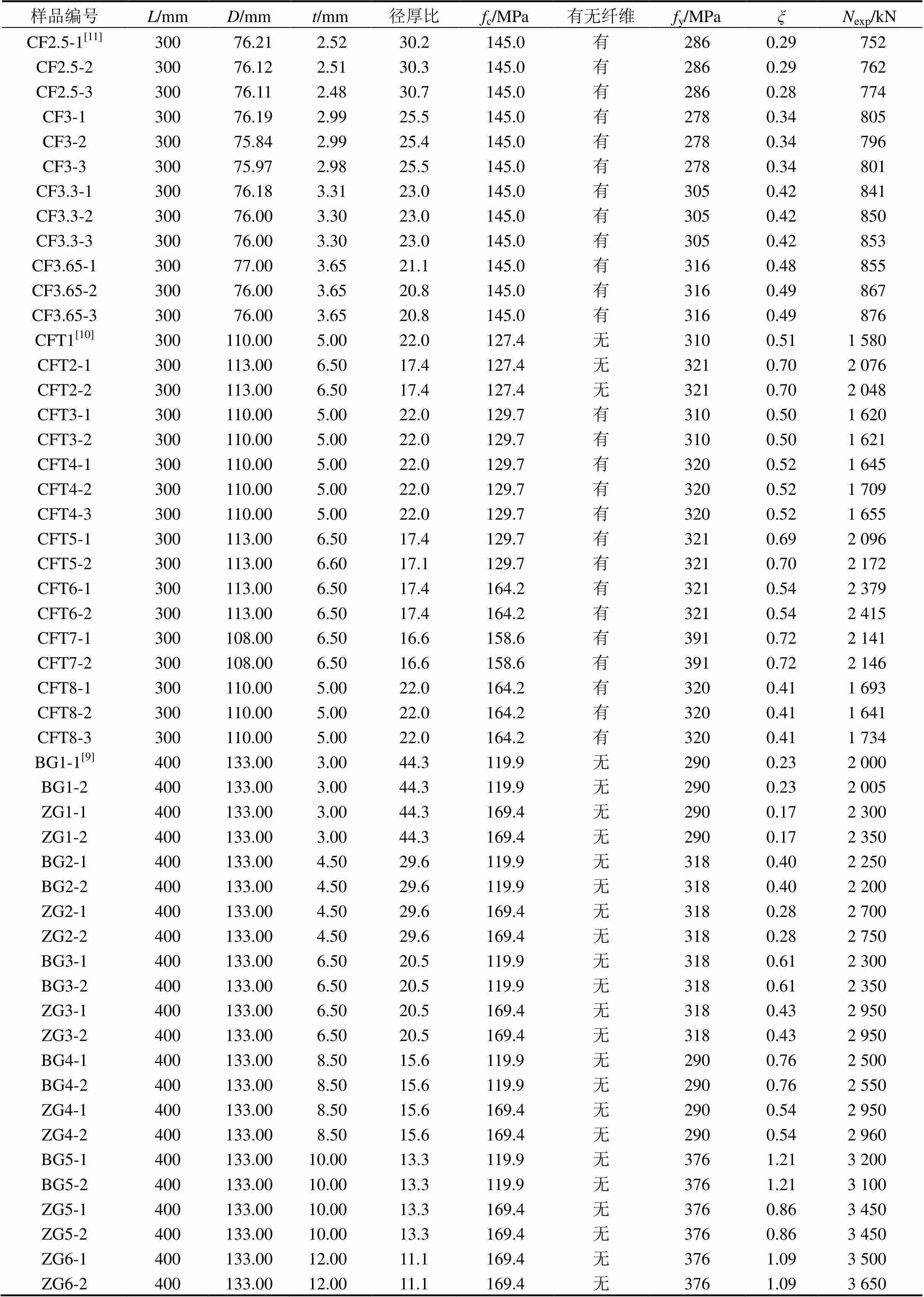
表1 試件參數

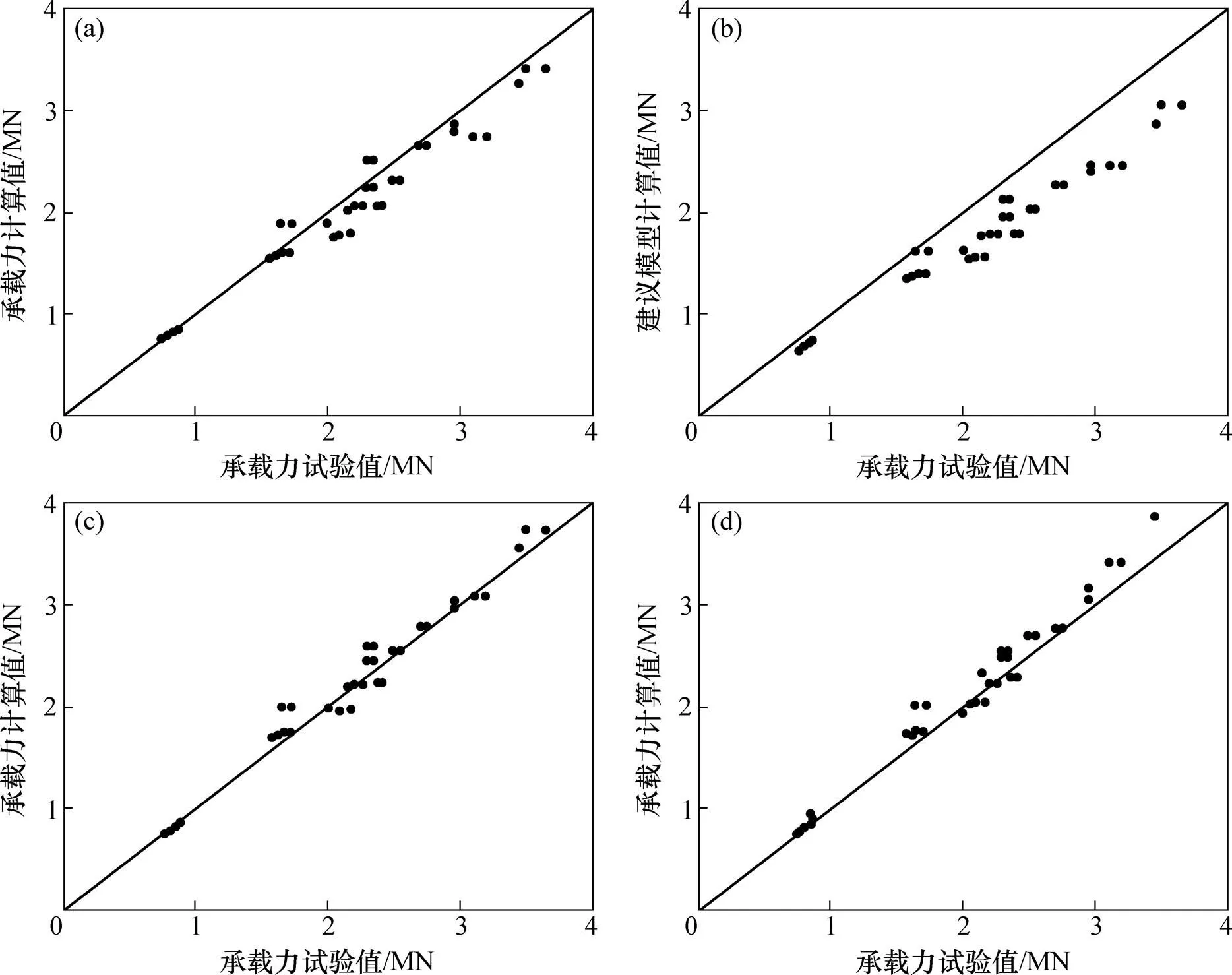
(a) 建議模型中承載力計算值與試驗值比較；(b) ACI中承載力計算值與試驗值比較； (c) EC4中承載力計算值與試驗值比較；(d) CECS28:2012中承載力計算值與試驗值比較

表2 不同方法試件軸壓承載力比較

從圖2可以看出：本文建議模型與EC4方法的承載力計算值與試驗值較吻合；ACI方法因為乘以折減系數0.85，計算結果較試驗結果偏小；CECS28:2012方法中承載力計算值比試驗值大，安全性較低。

不同方法試件承載力比較見表2。從表2可以看出：與建議模型相比，EC4方法試件承載力平均值最接近試驗值，且對應的標準差也更小，但承載力保證率(即承載力試驗值小于承載力計算值的試件個數占總個數的比例)只有58.8%，遠小于建議模型的86.3%。因此，綜合考慮精度和可靠度，建議模型更適合在設計中使用。

3 圓鋼管UHPC短柱軸壓變形能力計算模型

為評價圓鋼管UHPC短柱的軸壓變形能力，需要計算得到圓鋼管UHPC短柱軸壓受力全過程荷載?位移曲線。為此，本文分別采用基于Mander模型的圓鋼管約束UHPC單軸受壓本構模型和能夠考慮環向應力影響的鋼管單軸受壓本構模型，并將試驗結果與由上述2種材料模型計算得到的荷載?位移曲線進行對比，驗證本文方法的正確性。

3.1 基于Mander模型的圓鋼管約束UHPC單軸受壓本構模型

Mander模型能夠較好地考慮各種約束形式對混凝土的約束效果[24]，在抗震設計中得到了較廣泛的應用，其表達式如下：

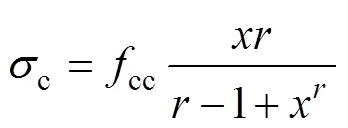
式中：和為計算參數，=c/cc，=c/(c?sec)；割線模量sec=cc/cc。

因此，利用Mander模型確定圓鋼管約束UHPC單軸受壓應力應變關系，需要的參數包括無約束UHPC的彈性模量c，以及約束UHPC的峰值應力cc和對應的應變cc。

GRAYBEAL根據試驗研究結果，建議無約束UHPC的彈性模量計算公式[2]為

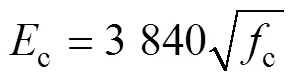
關于圓鋼管約束UHPC的峰值應力cc和對應的應變cc的計算方法尚未見報道。

SUGANO等[25]通過試驗給出了箍筋約束UHPC峰值應力時對應的應變的計算公式為

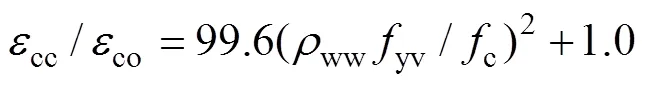
式中：ww為面積配箍率；yv為箍筋屈服強度；co為無約束UHPC的峰值應力對應的應變，其計算公 式[25]為

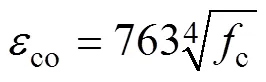
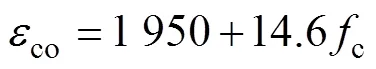
(a) CF2.5-3；(b) CF3.0-1；(c) CF3.3-1；(d) CF3.65-1；(e) BG3-1；(f) BG4-1；(g) BG5-1；(h) ZG2-1；(i) ZG3-1；(j) ZG5-1

1—試驗結果；2—建議模型；3—UHPC；4—鋼管。

圖3 不同試件荷載?位移曲線比較

Fig. 3 Comparisons of loading-displacement curves for different specimens

本文取式(37)和式(38)計算所得co的平均值作為計算結果，即

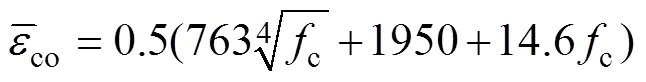
本文采用橫向約束等效原則，給出圓鋼管約束UHPC峰值應力時對應的應變計算公式為

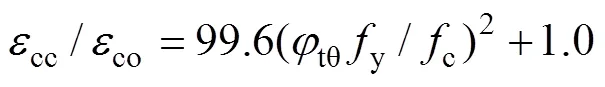
圓鋼管約束UHPC的峰值應力cc計算公式如下：

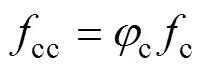
3.2 考慮環向應力影響的圓鋼管單軸受壓本構模型

為考慮環向應力的影響，對理想彈塑性模型進行修正，將修正后的理想彈塑性模型作為圓鋼管單軸受壓本構模型。考慮環向應力影響的修正后圓鋼管單軸受壓應力s為

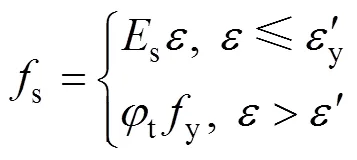
3.3 軸壓變形能力計算模型試驗驗證

選擇10根試件，驗證圓鋼管UHPC短柱軸壓變形能力計算模型的準確性。不同試件荷載?位移曲線如圖3所示。由圖3可以看出：建議模型中各試件荷載?位移曲線與試驗中試件荷載?位移曲線較吻合。

4 結論

1) 與EC4，ACI和CECS28: 2012規范方法相比，本文提出的圓鋼管UHPC短柱軸壓承載力計算模型兼顧了計算精度和可靠度，可用于工程設計。

2) 利用基于Mander模型的圓鋼管約束UHPC單軸受壓本構模型和考慮環向應力影響的圓鋼管單軸受壓本構模型可以得到圓鋼管UHPC短柱軸壓全過程荷載?位移曲線，且其與試驗結果較吻合。

[1] GRAYBEAL B A. Material property characterization of ultra-high performance concrete[R]. Washington D C, USA: Federal Highway Administration, 2006: 1.

[2] GRAYBEAL B A. Compressive behavior of ultra-high-performance fiber-reinforced concrete[J]. ACI Materials Journal, 2007, 104(2): 146?152.

[3] GRAYBEAL B A, BABY F. Development of direct tension test method for ultra-high-performance fiber-reinforced concrete[J]. ACI Materials Journal, 2013, 110(2): 177?186.

[4] 張哲, 邵旭東, 李文光, 等. 超高性能混凝土軸拉性能試驗[J]. 中國公路學報, 2015, 28(8): 50?58. ZHANG Zhe, SHAO Xudong, LI Wenguang, et al. Axial tensile behavior test of ultra high performance concrete[J]. China Journal of Highway and Transport, 2015, 28(8): 50?58.

[5] 徐世烺, 蔡向榮, 張英華. 超高韌性水泥基復合材料單軸受壓應力-應變全曲線試驗測定與分析[J]. 土木工程學報, 2009, 42(11): 79?85. XU Shilang, CAI Xiangrong, ZHANG Yinghua. Experimental measurement and analysis of the axial compressive stress-strain curve of ultra high toughness cementitious composites[J]. China Civil Engineering Journal, 2009, 42(11): 79?85.

[6] 徐世烺, 李賀東. 超高韌性水泥基復合材料研究進展及其工程應用[J]. 土木工程學報, 2008, 41(6): 45?60. XU Shilang, LI Hedong. A review on the development of research and application of ultra high toughness cementitious composites[J]. China Civil Engineering Journal, 2008, 41(6): 45?60.

[7] 鄭文忠, 呂雪源. 活性粉末混凝土研究進展[J]. 建筑結構學報, 2015, 36(10): 44?58. ZHEN Wenzhong, Lü Xueyuan. Literature review of reactive powder concrete[J]. Journal of Building Structures, 2015, 36(10): 44?58.

[8] 金何偉, 劉中憲, 劉申永, 等. 鋼管超高強鋼纖維混凝土柱抗爆性能試驗研究[J]. 建筑結構, 2016, 46(4): 45?49. JIN Hewei, LIU Zhongxian, LIU Shenyong, et al. Experimental study of ultra-high performance fiber reinforced concrete filled steel tube columns under blast loading[J]. Building Structures, 2016, 46(4): 45?49.

[9] 吳炎海, 林震宇. 鋼管活性粉末混凝土軸壓短柱受力性能試驗研究[J]. 中國公路學報, 2005, 18(1): 57?62. WU Yanhai, LIN Zhenyu. Experimental study of behavior on RPC filled steel tubular stub columns under axial compression[J]. China Journal of Highway and Transport, 2005, 18(1): 57?62.

[10] 林震宇, 吳炎海, 沈祖炎. 圓鋼管活性粉末混凝土軸壓力學性能研究[J]. 建筑結構學報, 2005, 26(4): 52?57. LIN Zhenyu, WU Yanhai, SHEN Zuyan. Research on behavior of RPC filled circular steel tube columns subjected to axial compression[J]. Journal of Building Structures, 2005, 26(4): 52?57.

[11] 田志敏, 張想柏, 馮建文, 等. 鋼管超高性能 RPC 短柱的軸壓特性研究[J]. 地震工程與工程振動, 2008, 28(1): 99?107.TIAN Zhimin, ZHANG Xiangbo, FENG Jianwen, et al. Characteristics of RPC-filled steel tubular puncheons with ultra high performance subjected to axial compressive loading[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(1): 99?107.

[12] GULER S, ?OPUR A, AYDOGAN M. Axial capacity and ductility of circular UHPC-filled steel tube columns[J]. Magazine of Concrete Research, 2013, 65(15): 898?905.

[13] 羅華, 季文玉, 閆志剛, 等. 加載方式對鋼管活性粉末混凝土短柱抗壓性能影響的研究[J]. 鐵道學報, 2014, 36(9): 105?110.LUO Hua, JI Wenyu, YAN Zhigang, et al. Research on influence of loading methods on compressive behavior of reactive powder concrete filled steel tube stub columns under axial loads[J]. Journal of the China Railway Society, 2014, 36(9): 105?110.

[14] 鐘善桐. 鋼管混凝土結構[M]. 北京: 清華大學出版社, 2003: 141?143. ZHONG Shantong. The concrete-filled steel tubular structures[M]. Beijing: Tsinghua University Press, 2003: 141?143.

[15] 韓林海, 楊有福. 現代鋼管混凝土結構技術[M]. 中國建筑工業出版社, 2007: 83?85. HAN Linhai, YANG Youfu. Technology of modern steel tube concrete structure[M]. China Building Industry Press, 2007: 83?85.

[16] ACI 318-05, Building code requirements for structural concrete and commentary[S].

[17] 蔡紹懷. 現代鋼管混凝土結構[M]. 人民交通出版社, 2003: 45?54. CAI Shaohuai. Modern steel tube confined concrete structures[M]. China Communications Press, 2003: 45?54.

[18] SAKINO K, NAKAHARA H, MORINO S, et al. Behavior of centrally loaded concrete-filled steel-tube short columns[J]. Journal of Structural Engineering, 2004, 130(2): 180?188.

[19] 周緒紅, 劉界鵬, 張素梅. 圓鋼管約束鋼筋混凝土短柱的軸壓力學性能[J]. 工程力學, 2009, 26(11): 53?59. ZHOU Xuhong, LIU Jiepeng, ZHANG Sumei. Behavior of circular tubed reinforced concrete stub columns under axial compression[J]. Engineering Mechanics, 2009, 26(11): 53?59.

[20] BS EN 1994-1-1: 2004, Eurocode 4: design of composite steel and concrete structures—part 1-1, general rules and rules for buildings[S].

[21] FEHLING E, SCHMIDT M, WALRAVEN J, et al. Ultra-high performance concrete UHPC: fundamentals, design, examples[M]. Berlin, Germany: John Wiley & Sons, 2014: 44.

[22] CHOI K K, XIAO Y. Analytical studies of concrete-filled circular steel tubes under axial compression[J]. Journal of Structural Engineering, 2009, 136(5): 565?573.

[23] CECS28:2012, 鋼管混凝土結構設計與施工規程[S]. CECS28:2012, Technical specification for concrete-filled steel tubular structures[S].

[24] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804?1826.

[25] SUGANO S, KIMURA H, SHIRAI K. Study of new RC structures using ultra-high-strength fiber-reinforced concrete (UFC)-The challenge of applying 200 MPa UFC to earthquake resistant building structures[J]. Journal of Advanced Concrete Technology, 2007, 5(2): 133?147.

An analytic model for axial load capacity and deformation capacity of short columns of circular UHPC filled steel tube

WANG Zhen1, WANG Jingquan1, 2, LIU Tongxu1, XIU Hongliang1

(1. Key Laboratory of Concrete and Prestressed Concrete Structure of China Ministry of Education, Southeast University, Nanjing 210096, China; 2. National Prestress Engineering Research Center, Southeast University, Nanjing 210096, China)

Due to force equilibrium and deformation compatibility, the expressions of steel tube reduction coefficient and core concrete strengthen coefficient were deduced to study the improvement of confinement of steel tube on axial strength of ultra high performance concrete (UHPC) and the reduction of circumferential stress on axial strength of steel tube. Based on the above two factors, an analytic model for load capacity of circular UHPC filled steel tube stub columns was established, and the proposed model was compared with several conventional standard methods. According to the equivalence principle of transverse confinement, the axial compressive constitutive model was established for circular steel tube confined UHPC based on Mander model. Ideal elastic-plastic model was modified to take the effect of circumferential stress into account for the axial compressive constitutive model of circular steel tube. The two above models were used to simulate the axial compressive load-deformation curve of short columns with circular UHPC filled steel tube. The results show that compared with several methods given by standards, the axial load capacity model shows good calculation precision and reliability, the axial compressive load-deformation curve given by the proposed model is in good agreement with that of trial results.

concrete filled steel tube; ultra high performance concrete; axial load capacity; deformation capacity; deformation compatibility

10.11817/j.issn.1672?7207.2019.02.023

TU398.6

A

1672?7207(2019)02?0428?09

2018?04?01；

2018?06?06

國家自然科學基金資助項目(51438003)；國家科技支撐計劃項目(2011BAJ09B02)；江蘇高校優勢學科建設工程資助項目(CE02-1-4)(Project(51438003) supported by the National Natural Science Foundation of China; Project(2011BAJ09B02) supported by National Key Technology Research and Development Program of China; Project(CE02-1-4) supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions)

王景全，博士，教授，從事組合結構橋梁和橋梁抗震等研究；E-mail：wangjingquan@seu.edu.cn

(編輯 伍錦花)