結構元線性生成的模糊數列的收斂性

舒天軍, 莫智文

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

模糊數列作為模糊分析學的一個重要組成部分,可應用于近似理論、測度理論、級數理論等諸多領域.基于模糊距離,關于模糊數列極限的定義,一些學者[1-17]作了討論.結構元生成模糊數的定義由郭嗣琮[18]于2002年提出,至今已經產生了許多有意義的成果.本文根據文獻[19]給出的模糊距離,在水平收斂的前提下,定義了一種新的結構元線性生成的模糊數列的收斂定義,并用這種收斂定義研究了結構元線性生成的模糊數列的基本性質.同時定義了結構元線性生成的模糊數項級數且探討了其性質.

1 預備知識

定義1.1[18]E是實數域R上的模糊集,隸屬函數記為E(x),x∈R.如果E(x)滿足下述性質：

1)E(0)=1,E(1+0)=E(-1-0)=0;

2) 在區間[-1,0)和(0,1]上,E(x)分別是單調遞增右連續函數和單調遞降左連續函數;

3) 在區間(-∞,-1)或(1,+∞)上,E(x)=0,

則稱模糊集E為R上的模糊結構元.

顯然,模糊結構元E是R上的正則凸模糊集,是有界閉模糊集.

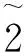
則

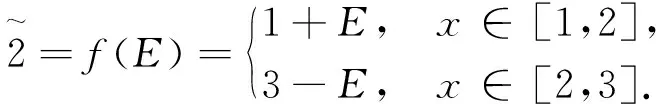
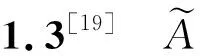
?a∈R,r∈R+}.

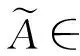
因為[-1,1]上所有同序標準單調有界函數關于“≤”(或“≥”)構成偏序集,則((E),≤)構成偏序集.

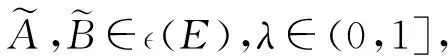
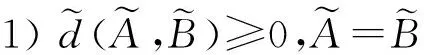
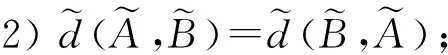
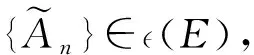
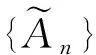
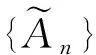
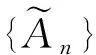
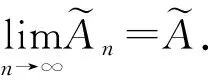
2)的證明類似1).

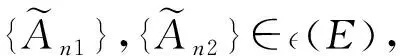
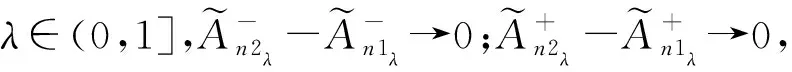
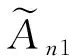
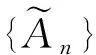
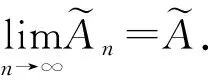
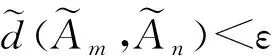
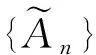
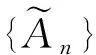
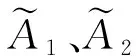
當n>N2時有

則令N={N1,N2},當n>N時有

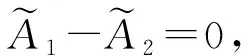
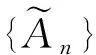
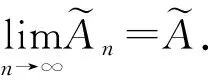
則

且

可以推出

且

則有

且

所以

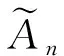
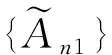
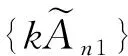
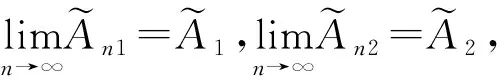
當n>N2時有

令N=min{N1,N2},則當n>N時有

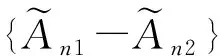
則取N≥N1,當n>N時有

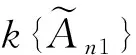
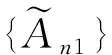
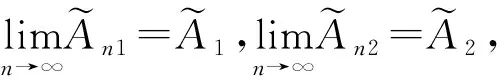
則有

且

從而

當n>N2時有

則有

且

從而

令N=min{N1,N2},當n>N時有

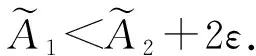
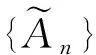
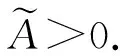
則

且

有

且

所以

定理得證.

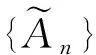
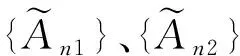
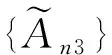
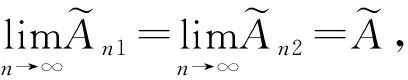
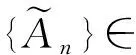
特別地,如果模糊數項級數每一項都是正數,則稱該數項級數為正項級數.

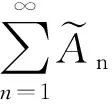
由定理2.3易證.

推論3.1對模糊收斂級數去掉、增加或改變有限個項,該模糊級數依然收斂.

推論3.2在收斂模糊級數中任意加括號,模糊級數亦收斂且和不變.

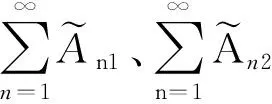
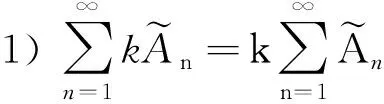
由定理2.6易證.

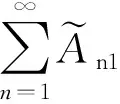
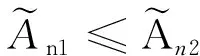
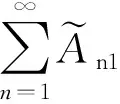
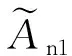
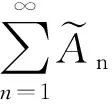
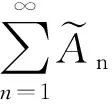
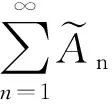
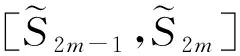
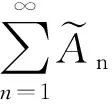
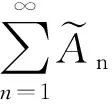
定理3.6模糊級數絕對收斂則一定收斂.

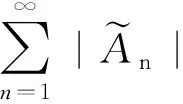
由絕對值不等式可得

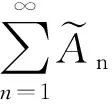
推論3.4若模糊級數絕對收斂,則任意排序數列后的模糊級數也絕對收斂,且其和與原模糊級數和相同.