非線性項帶導數的三點邊值問題正解的 存在性與多解性
康宏亮, 肖鴻民
(西北師范大學 數學與統計學院, 甘肅 蘭州 730070)
1 引言及主要結果
基于豐富的實際應用背景,非線性常微分方程邊值問題正解的存在性和多解性問題在常微分方程研究領域顯得尤為重要.對于經典的三點邊值問題,近30年來已取得了一定結果,參見文獻[1-15]及其相關文獻.
特別地,1994年,Wang[1]在f∈C([0,∞),[0,∞)),a∈C([0,1),[0,∞))且a(t)在(0,1)的任意子區間內不恒為0的條件下構造錐
K={u(t):u∈C[0,1],u(t)≥0,
然后運用錐上的不動點理論獲得了二階微分方程Robin邊值問題
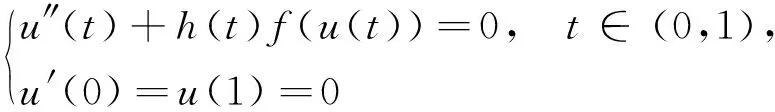
(1)
在非線性項滿足超線性或次線性條件下其正解的存在性.
1999年,Ma[2]研究三點邊值問題
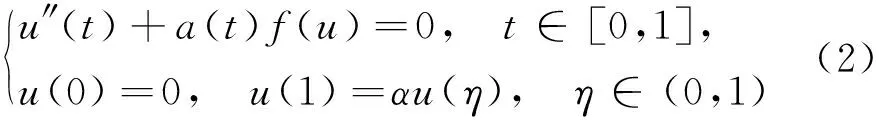
時提出了研究這類問題的關鍵條件
0<αη<1,
并且通過構造錐
K={u∈C[0,1]:u(t)≥0,
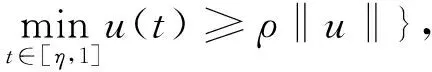
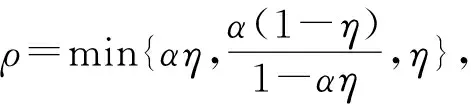
文獻[1-2]中的f均不依賴于u′,因為f(u′)在C[0,1]內研究,將無法構造錐,繼而無法運用錐上的不動點定理研究相應問題正解的存在性.但經過仔細分析發現,對于邊界條件比較特別的形式而言,當非線性項上帶導數時,可以在C1[0,1]中構造錐,進而使用不動點指數理論獲得該問題正解的存在性和多解性.基于此,本文將研究系統
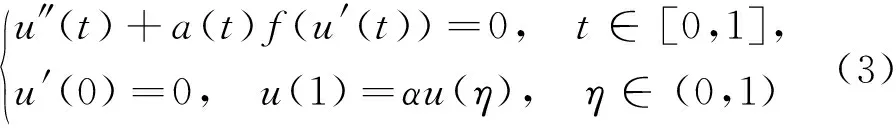
正解的存在性和多解性,其中,α>0,0<αη<1.
本文總假定:
(H1)f:[0,∞)→[0,∞)連續;
(H2)a∈C([0,1],[0,∞))且在(0,1)的任意子區間內a(t)不恒為0;
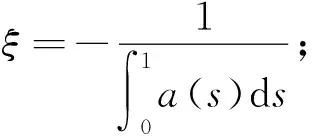
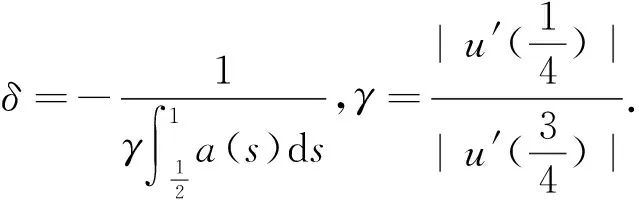
本文主要結果如下:
定理1假定(H1)和(H2)成立,若f滿足下列條件之一:
(i) (超線性)f0=0且f∞=∞;
(ii) (次線性)f0=∞且f∞=0,
則邊值問題(3)至少存在一個正解,其中
定理2假定(H1)~(H3)成立且f0=f∞=∞,那么問題(3)至少存在2個正解x1、x2,使得
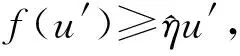
0<‖x1‖ 定理3假定(H1)、(H2)和(H4)成立且f0=f∞=0,那么問題(3)至少存在2個正解x1、x2,使得 0<‖x1‖ 本文主要工具為: 引理1[16]設X為Banach空間,K?X是X中的一個錐.定義Kp={x∈K|‖x‖≤p,p>0},?Kp={x∈K|‖x‖=p},假設A:Kp→K是一個全連續算子,當x∈?Kp時Ax≠x,則: (i) 如果當x∈?Kp時,有‖x‖≤‖Ax‖成立,則i(A,Kp,K)=0; (ii) 如果當x∈?Kp時,有‖x‖≥‖Ax‖成立,則i(A,Kp,K)=1. 引理2[15]設α≠1,則對y∈C[0,1],問題 (4) 有唯一解 u∈[0,1], 其中 因此Hammerstein積分算子的核為 其中 且 引理3A(K)?K,且A是全連續算子. 證明 u″(t)=-a(t)f(u′(t))≤0. 故A(K)?K.由f的連續性及Arzela-Ascoli定理可知A:K→K是全連續算子. 定理1的證明定義錐K={u∈C1[0,1],u′≤0,u在[0,1]上是向上凸的,u′(0)=0,u(1)=αu(η)}. 容易驗證錐K中的元素u滿足 (5) 這里 (i) 超線性情形.因為f0=0,取H1<0,使得對H1≤u′≤0,有f(u′)≤ηu′,其中η<0滿足 因此若u∈K,‖u‖=-H1,則由 記 Ω1:={u∈X:‖u‖≤-H1}, 則 ‖Au‖≤‖u‖,u∈K∩?Ω1. 故 ‖Au‖≥‖u‖,u∈K∩?Ω2. 記 Ω1:={u∈X:‖u‖<-H1}, 則 ‖Au‖≥‖u‖,u∈K∩?Ω1. 所以‖Au‖≤‖u‖. 所以無論何種情況,只要令Ω2:={u∈X:‖u‖<-H2},就有‖Au‖≤‖u‖,u∈K∩?Ω2.由引理1(ii)知問題(3)有一個正解. 定理2的證明令M<0,使得 (6) 由f0=f∞=∞與引理1(ii)知,若存在p 因此,由引理1得 i(A,Kr,K)=0. (7) 對同樣的滿足(6)式的M,由f0=f∞=∞可知,存在R1<0,使得f(u′)≥Mu′,?u′≤R1.令R 因此,由引理1得 i(A,KR,K)=0. (8) 另一方面,由條件(H3),若u′∈?Kp,則 因此,由引理1得 i(A,Kp,K)=1. (9) 由(7)~(9)式得 i(A,KRKp,K)=-1,i(A,KpKr,K)=1. 因此,A在KRKp上有一個不動點x1,在KpKr上有一個不動點x2,均為問題(3)的解,并且x1(t)>0,x2(t)>0,t∈(0,1). 定理3的證明由f0=f∞=0,對?ε<0,存在W<0,使得f(u′)≤W+εu′,?u′≤0,t∈[0,1],那么 因此,令ε充分小且R i(A,KR,K)=1. (10) 同樣地,對p i(A,Kr,K)=1. (11) 另一方面,由(H4),對u′∈?Kp有 因此,由引理1得 i(A,Kp,K)=0. (12) 由(10)~(12)式得A有2個不動點,則問題(3)有2個正解. 例1考慮非線性項帶導數的二階三點邊值問題 滿足超線性情形,則由定理1可知,問題(13)至少存在一個正解.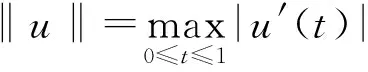
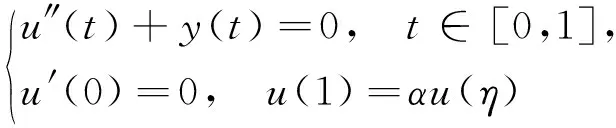
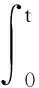
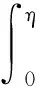
2 主要結果的證明
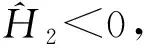
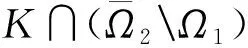
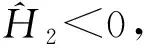
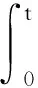
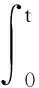
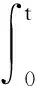
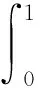
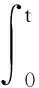
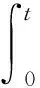
3 應用