一種基于OCSVM的PLC網絡異常檢測技術

何世敏，劉嘉勇，鄭榮鋒

（1.四川大學電子信息學院，成都 610065；2.四川大學網絡空間安全學院，成都 610065）

0 引言

由于在實際的工業控制系統中，采集到的正常流量樣本數遠多于異常流量的樣本數。所以采用傳統的支持向量機算法對正負樣本分類的準確率會較低。而單類支持向量機算法利用一種類型的樣本數據就可以訓練出檢測模型，并且也不需要對數據類型進行標記。該算法是通過核函數把輸入的工控流量數據映射到高維特征空間，并在此空間中找出最大超平面來分類出異常和正常類型[1-3]。文獻[1]提出了一種基于單類支持向量機和遞歸K領域方法結合的異常檢測技術，通過不斷調節單類支持向量機算法中核函數的參數g，算法本身參數C和設置K領域的閾值來提高檢測異常流量的準確率。文獻[2]中，作者通過使用單類支持向量機和增量學習的方法分類正常和異常的數據類型。文獻[3]中，作者通過在單類支持向量機模型和K-means方法來檢測工控網絡流量。這些檢測方法都能夠分類出異常類型，但是對單類支持向量機中核函數的參數g和算法的本身參數C的優化，傳統的方法是采用網格搜索法。該方法雖然具有全局的搜索能力，但是耗時多，效率低[4]。此外，在實際的工業操作過程中，由于獲得的樣本量大，數據維數過多，會使得訓練模型和異常檢測時間復雜度高[2-3]。

本文針對西門子S7協議的通信特征和減少模型計算時間消耗的問題，采用單類支持向量機的算法建立異常檢測模型，同時結合了主成分分析法對數據的特征進行降維，減少了模型的訓練和檢測時間。

1 特征選擇

在傳統的針對網絡層和傳輸層的網絡異常檢測研究中，一般選擇源端口、目的端口、源IP、目的IP、IP包總長度、TCP總長度、窗口流量大小作為能夠代表原數據包的特征[5]。針對在實際情況中，對工控網絡應用層的攻擊手段較多的特點，本文除此之外，還對應用層的S7協議進行了特征選擇。

S7協議的通信端口是102端口，工作在TPKT協議和COTP協議之上。該協議被IP頭、TCP頭、TPKT頭和COTP頭封裝。其數據包結構如圖1所示。

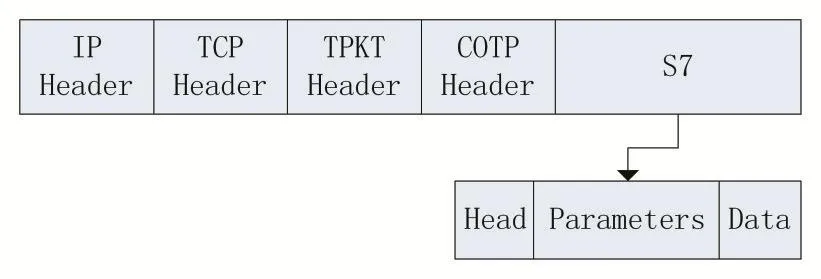
圖1 S7協議數據包結構

根據文獻[12]對S7協議的分析，Header部分是由Protocol Id、ROSCRT、Protocol Data Unit ReferenceData、Length、Parameter length字段組成，其中除了Protocol Data Unit Reference字段的值會隨著請求與響應命令的發送增加外，其他字段的值都是固定不變的。因此本文把Protocol Data Unit Reference字段作為特征之一。

Parameters部分由Parameters set和Parameter Data字段組成。在Parameters set中Function字段代表的是PLC的操作，而在一般的攻擊行為中，都會通過改變Function的值來改變對PLC的操作，因此，Function字段也作為本文的特征之一。

Parameter Data字段定位PLC中的內存信息[6]，該字段結構如圖2所示。為了提取出內存地址，字節大小，本文把Parameter Data整個字段作為特征。

圖2 Parameter Data結構

Data部分中存儲的是PLC操作的數值，本文把如圖3所示的字段作為特征。因為文中在異常檢測實驗中，為了獲得異常流量數據，會在實驗平臺上運行多種攻擊腳本，其中一種就是偽造圖中所示字段數值來改變發電機轉速。

圖3 Data字段

2 特征降維

假設采集到的PLC和上位機之間的網絡流量中數據包有m個，經過特征選擇之后，每個數據包中共有n=19個特征代表原始樣本的信息,用矩陣形式表達如下：

在特征選擇的過程中選擇的有效特征越多，越能體現原始樣本的信息。但是在實際的工控系統中，由于樣本量大和矩陣M的維多數的原因，會造成訓練模型和檢測異常的時間消耗過多的問題。為此，本文在對數據包特征選擇之后，還采用主成分分析法對這些提取出的特征進降維處理。該算法流程圖如圖4所示。

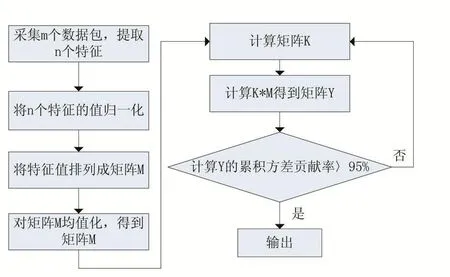
圖4 主成分分析法流程

步驟一：在經過特征選擇之后，確定S7協議數據包的n=19個特征，用并將特征從網絡層，傳輸層和應用提取出。

步驟二：將n個特征的值歸一化。歸一化處理是因為提取出的特征往往是具有不同的量綱單位和大小，這樣的數據如果經過降維處理，會使得結果不在同一數據范圍類,不具有可比性。本文采用的方法是首先求得每個數據包的n個特征的均值 μ和標準差δ，然后根據公式ni'=(ni-μ)/δ計算歸一化后的特征值。其中ni代表的是第i個特征值，用ni'代替原來的ni。

步驟三：把經過歸一化處理的特征排列成矩陣M。 M=(N1,N2,N3…Nm)，其中 Ni=(n1',n2'…nn')T。

步驟四：計算矩陣M1。根據主成分分析法的原理，在變換過程中需要對矩陣M進行均值化。目的是為了減少那些遠離平均值的點帶來的降維誤差，同時也是為了對歸一化做進一步的規范[7]。均值化的第一步是對M中的樣本求均值向量，然后用M中的樣本減去均值向量得到新的矩陣M1。

步驟五：計算矩陣K。首先計算特征M1矩陣的協方差矩陣，然后求出協方差矩陣的特征向量和特征向量對應的特征值，最后將特征向量按照特征值的大小降序排列，得到矩陣K。

步驟六：計算矩陣Y。去均值化之后，將樣本中的n個特征經過投影映射，過程如下：

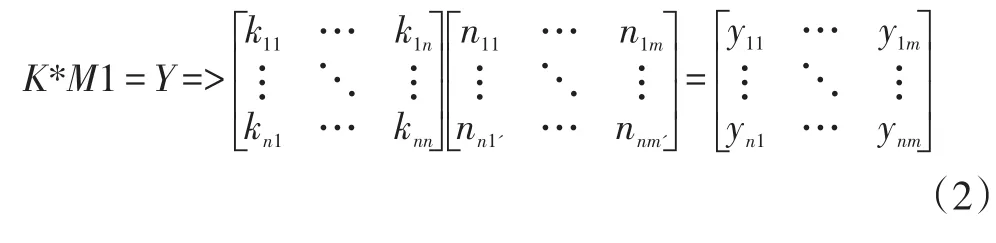
所得的結果Y就是由新特征組成的矩陣，其中yij=(ki1n1j'+ki2n2j'+…kinnnj')。

3 單類支持向量機模型構建

3.1 模型構建方法

單類支持向量機的本質是把原點看成異于訓練樣本類型的點，通過非線性映射關系，把在低維空間中的數據映射到高維空間中，并在這個空間中找出一個超平面，使得原點到這個平面的距離盡可能地大[9-10]。該算法流程如圖5所示。

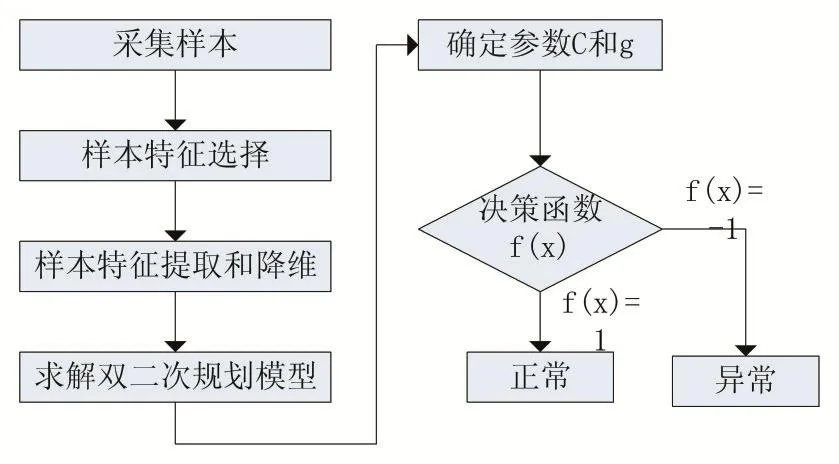
圖5 單類支持向量機模型

步驟一：在PLC和上位機之間采集樣本流量數據。

步驟二：確定樣本的特征值，個數為n，并提取出這些特征值,用主成分分析法對特征值降維,降維過后的特征值個數為k。

步驟三：求解雙二次規劃模型。把經過前兩步處理之后的樣本用X={(xi),i=1,2,3…m}表示，其中每個xi都有k個特征。根據單類支持向量機的原理，為了使得樣本能夠通過非線性映射關系σ(xi)投射到高維空間中，先在高維空間中構造一個超平面為Wσ-ρ=0。其中W是超平面的法向量，ρ為偏置量。根據文獻[2]可知，映射過程如下所示：

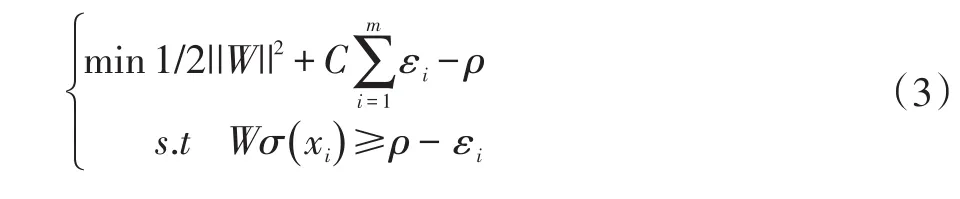
式中xi就是輸入的樣本。εi是一個懲罰系數，系數C=1/(μm),μ是一個權衡系數,m是樣本的個數。為簡化問題，單類支持向量機在映射過程中，引入了拉格朗日乘子式，將求解超平面的問題轉換為二次規劃問題[1]：

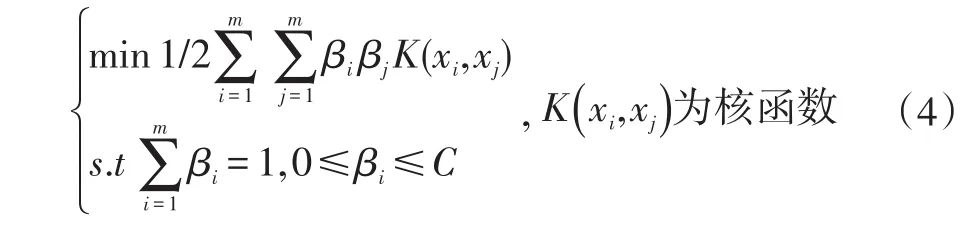
其中核函數是有多項式核函數，線性核函數，徑向基核函數。根據文獻[3]的實驗證明，選擇徑向基核函數（exp(-g‖xi-xj‖2)）的單類支持向量機的檢測準確率更高。

步驟四：確定參數C和g。

步驟五：在確定最優參數g與C之后，求得雙二次規劃模型的解為{W*,ρ*,ε*}，利用求得的解求出單類支持向量機的決策函數為 f(x)=sgn((W*)δ-ρ*)。該決策函數中sgn是一個符號函數，取值只有1或者-1，如果輸入樣本之后，結果 f(xi)=-1,那么這個樣本就被標記為異常類型輸出，如果結果 f(xi)=1，這個樣本就被標記為正常類型輸出。

3.2 基于人工蜂群算法的模型參數尋優

單類支持向量機的兩個參數g和C影響著算法的準確率，為了獲得最優參數，本文采用人工蜂群的方法。該方法與用粒子群求解最優參數方法相比，具有控制參數少的優點。

人工蜂群的方法是通過模仿蜜蜂采蜜的過程，把求解單類支持向量機最優參數的問題轉換為蜜蜂確定食物源位置問題[11-12]。該方法中的蜜蜂是分為采蜜蜂，觀察蜂和偵察蜂3種。人工蜂群算法將采蜜蜂和觀察蜂在食物源附近搜索新食物源以及偵察蜂在可行解空間中的隨機探索定義為一次迭代的過程，每次迭代所獲得的解質量都比上一次迭代獲得的解質量要高，當迭代次數接近無窮時，算法將以概率1收斂于全局的最優解[11]。

用人工蜂群確定最優參數g與C的方法如下：

以崗位能力點為標準，以項目為載體的過程教學模式具有系列考核指標，學習效果評價管理網絡信息化便于教師記錄過程信息與考核結果，避免了傳統紙質記錄的不便與管理的繁瑣。通過信息平臺向學生實時公開過程考核情況，以使學生了解自身的學習狀況，及時制定彌補措施，公開透明的評價方式也利于形成好的學習風氣。

步驟一：初始化參數。根據人工蜂群算法的原理，本文用核函數參數g和算法本身參數C組成的二維向量（g,C）來代表一個食物源的位置解。利用文獻[17]的結果，把循環次數設置50，最大迭代次數設置為1000，g和C的范圍設置為（0,1）,原始食物源的位置解個數設為N=20，用Xi=(g,C)i,i=1,2,...,N表示。其中(g,C)i是（0,1）之間隨機生成的。

步驟二：在原始解Xi的領域附近搜索新的解。由于Xi是由參數g和C組成的二維向量，所以搜索之后的新解也是g和C的二維向量。根據人工蜂群算法原理 ，新 解 vi2=Xi+random（0,1)×(Xi-Xk)。 其 中i,k=(1,2,3,…,20),且 i≠k 。

步驟四：比較vi2與Xi適應度的大小。如果vi2適應度大于Xi適應度，用vi2替代Xi。其中i=1,2,…,20。

步驟五：重新確定新解。根據步驟三中替換后的結果，計算結果中每個解被選擇的概率i,2,3,…,20，并根據概率Pi重新選擇解。把得到的新結果代入步驟二的公式中，重復步驟三四五，并記為一次循環。

步驟六：如果某些解經過循環50次，適應度沒有得到提高，就把對應的解放棄，并且用公式xi=(g,C)min+rand(0,1)×((g,C)max-(g,C)min)隨機生成新解替代原來放棄的解。

步驟七：計算迭代的次數。記步驟二至步驟六為一次迭代過程。若迭代的次數大于1000，輸出的解就是最優解，也就是最優參數g和C，若小于則返回步驟二。

4 實驗與結果分析

4.1 模型訓練與檢測

實驗代碼所用工具：Python 2.7，Python scapy模塊提取特征和scikit-learn機器學習庫。實驗采集的訓練樣本數據是工控實驗平臺中S7-300PLC和上位機之間的正常網絡流量數據。本文針對數據集中的單個數據包選擇的部分特征如表1所示。

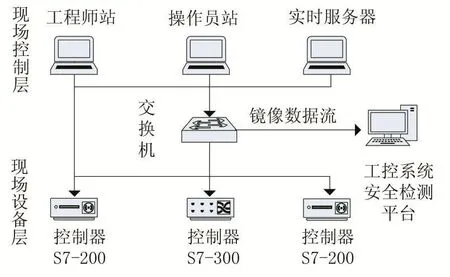
圖6 實驗平臺示意圖

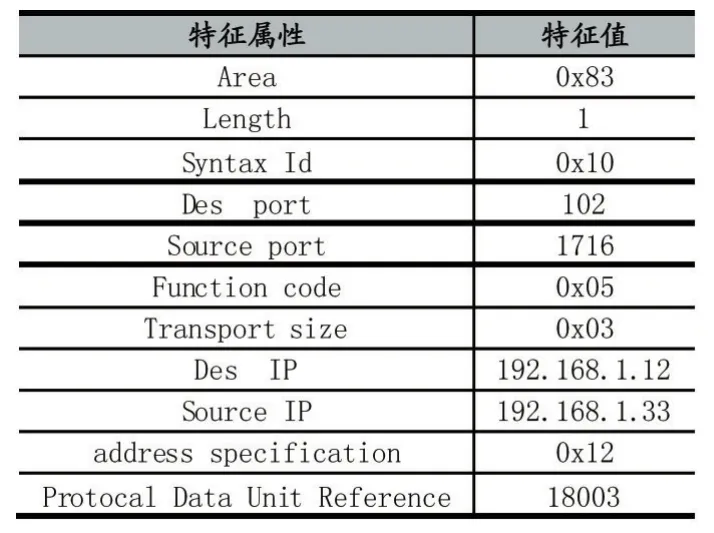
表1 數據包特征選擇

在經過特征提取之后，采用主成分分析法降維，結果如圖7所示。其中橫軸代表的是降維后的矩陣中的特征，也就是主成分的分量，縱軸代表的是各個主成分的累計方差貢獻率。由圖可以看出前11個主成分的累計方差的貢獻率已經達到了95%，所以可以把前11個主成分作為替代之前選擇的特征數據。

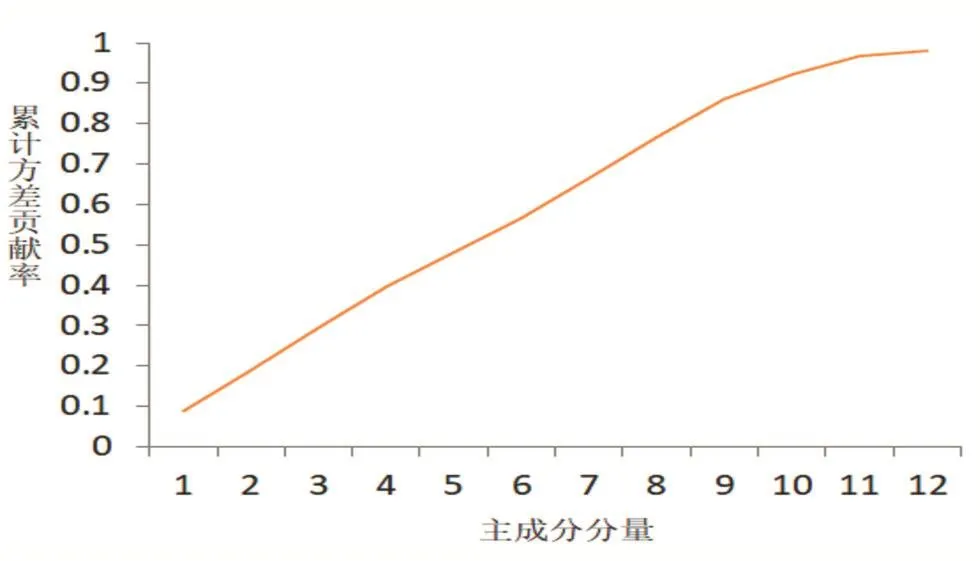
圖7 累計方差貢獻率

為了獲得測試數據集，本文在西門子實驗平臺上運行了三種攻擊腳本：

（1）中間人攻擊：在實驗平臺的正常工作過程中，操作員站對發電機轉速的控制是通過S7-300PLC的。當發電機的轉速達到一定的閾值后，實驗平臺的蜂鳴器會產生警報。中間人攻擊是改變了操作員站與PLC之間的數據，使得轉速超過閾值之后，蜂鳴器不工作[6]，數據集記為T1。

（2）轉數邏輯序列攻擊：在正常工作流程中，PLC和現場控制的發電機工作產生的數據包的序列都是有邏輯順序的，通過修改數據包的次序來改變PLC和發電機的工作邏輯，數據集記為T2。

（3）轉速值改變攻擊：手動修改操作員站發送給PLC的數據來改變發電機的轉速，數據集記為T3。

4.2 實驗結果分析

為了能夠更加準確的評估模型的性能，本文結合了分類的準確率和F1-score兩個評價指標。分準確率和F1-score基于混淆矩陣計算，其中混淆矩陣如表2所示。

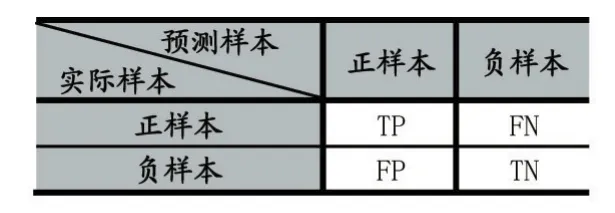
表2 分類器混淆矩陣

其中，TP表示實際和預測結果都是正樣本類型的樣本數。FN表示的是實際是正樣本但是預測結果是負樣本的樣本數。FP表示的是實際是負樣本但預測結果是正樣本的樣本數。TN表示的是實際和預測結果都是負樣本的樣本數。

分類準確率計算如公式（5）所示：

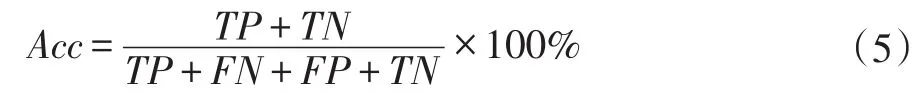
分類的精確度是表明測試集中被預測的正樣本中為實際正樣本的比例，召回率是表明被模型預測的正樣本占總正樣本的比例。由于精確度和召回率相互制約的，所以F1-score是精確度和召回率的調和值[13]，計算如過程如式（6-8）所示：

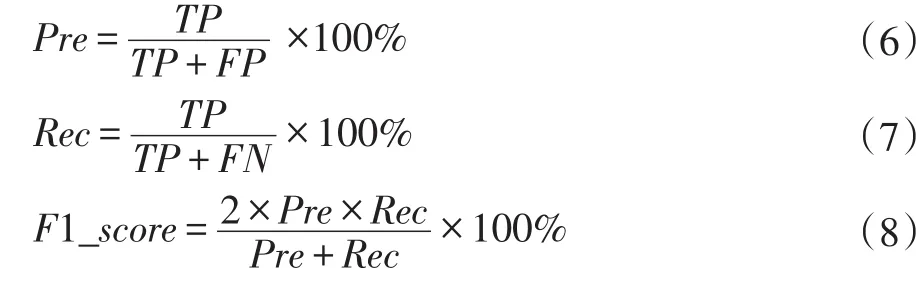
在模型訓練階段，用人工蜂群方法求得最優參數g=0.0123，C=0.462。本文對比了傳統的OCSVM的準確率和計算時間，結果如圖8和圖9所示。相比于傳統的OCSVM，本文的方法在降維之后依然保持著傳統OCSVM異常檢測的準確率，在數據集個數大于2000個時，傳統的OCSVM算法和本文采用的主成分分析結合OCSVM算法模型訓練的分類準確率都達到90%以上。但是在模型的訓練時間對比中，傳統的OCSVM算法消耗的平均時間比主成分分析結合OCSVM算法消耗的平均時間多46.45秒。

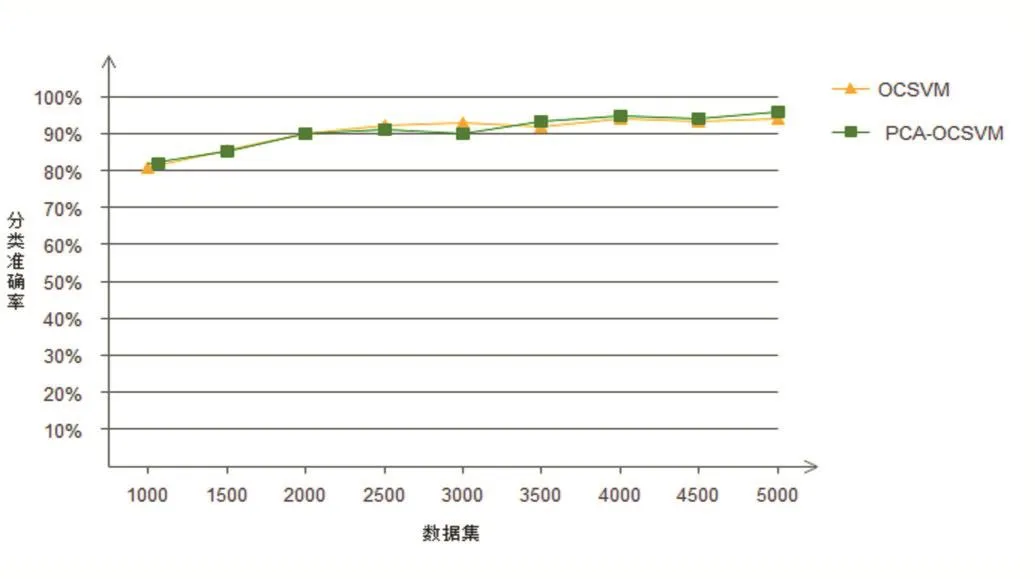
圖8 訓練模型的準確率

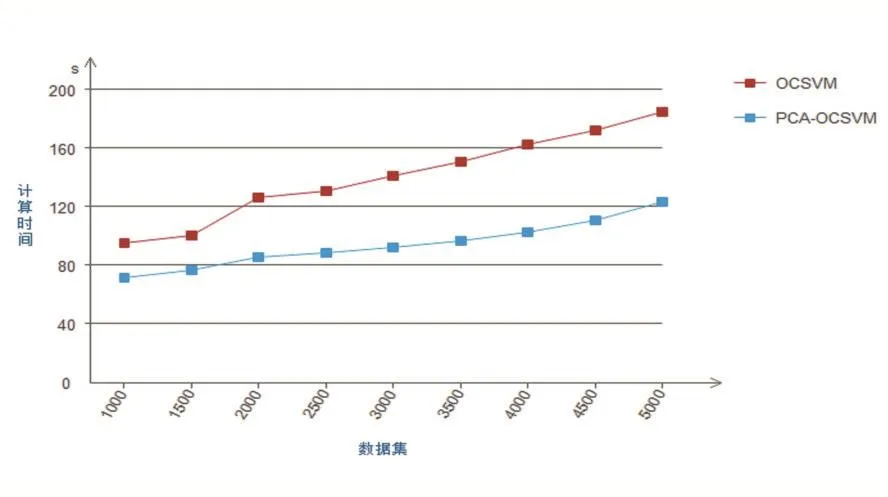
圖9 模型訓練時間對比

在使用相同用測試集T1,T2,T3的情況下，本文對比了傳統OCSVM算法的分類準確率，F1-score和模型檢測時間，如表3所示。

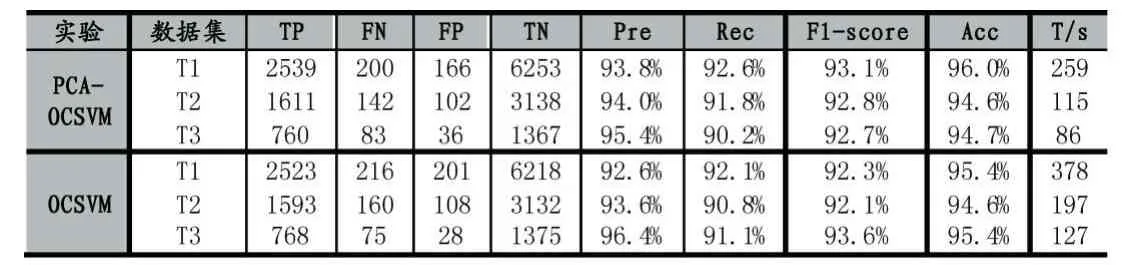
表3 異常檢測結果對比

實驗采集的三種攻擊腳本下的數據集T1,T2,T3數據包總數分別為9158,4993,2246。使用主成分分析結合單類支持向量機的方法在分類準確率Acc和F1-score上都保持著傳統支持向量機的90%以上的檢測性能。但是在檢測時間消耗方面，使用主成分分析結合單類支持向量機檢測數據集T1,T2,T3比使用傳統支持向量機檢測分別少119秒、82秒和41秒。

5 結語

本文主要是以西門子S7協議為研究對象，針對實際情況下工控網絡異常數據少，維數多的情況，在使用主成分分析法降維之后，采用單類支持向量機的方法來進行模型訓練和檢準精確度的同時，能有效減少模型運算時間的消耗。