某小型通用發動機動平衡分析及其對策

劉永根 楊海岳 李 進

（浙江中堅科技股份有限公司 浙江 永康 321300）

引言

某小型通用發動機是單缸、風冷、四沖程發動機。發動機曲軸連桿機構運動所產生的往復慣性力和旋轉慣性力是整車重要的振動源，可以通過對其進行動平衡分析，指出曲軸在結構設計上的不足之處，并提出在最少改變現有結構條件下的對策。

1 單缸發動機動平衡簡要分析

發動機工作時，曲柄連桿機構作復合平面運動。在力學上可采用雙集中質量系統來替代實際機構的質量分布，即一部分作為往復直線運動的質量mj，包括活塞組質量mp和連桿組換算到小頭中心的質量m1，它們集中作用在活塞銷中心，會產生直線往復慣性力Pj。另一部分為作旋轉運動的不平衡質量mr，包括曲柄銷換算質量mk、滾針軸承質量mg及連桿組換算到大頭中心的質量m2，它們集中作用于曲柄銷中心，會產生離心慣性力Pr。往復慣性力Pj和離心慣性力Pr按一定的周期交變地作用在發動機上，引起整機振動，使機器的平順性和舒適性大大降低。

1.1 往復慣性力P j

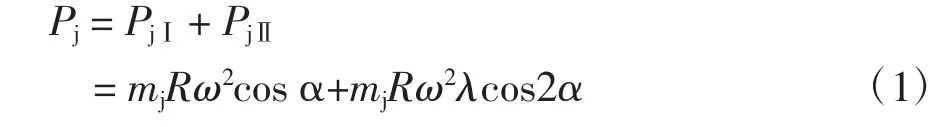
一般只取Ⅰ級往復慣性力PjⅠ分析已足夠，即方向沿著氣缸中心線。

1.2 離心慣性力P r

方向始終沿曲柄向外

由式（3）可知，若ω以某一恒定速度運轉時，Pr為一個大小不變的力[1]。

若要完全平衡Pj和Pr，則須配備結構復雜的雙曲軸平衡機構，即在氣缸中心線的兩側對稱安裝兩對帶平衡重的平衡軸。該方法所占空間較大，對小型發動機而言不切實際。一般多用簡單的過量平衡，即在曲軸上裝置較大的平衡重，此平衡重旋轉產生的離心力Pd，不僅平衡了離心慣性力Pr，還存在剩余離心力ΔP＝Pd－Pr，使其在Y軸（氣缸中心線方向）的分力ΔP cosα來平衡掉一部分Pj，但在X軸方向同時出現不平衡力ΔP sinα。實際上是將Pj中的一部分力從Y軸上轉移到X軸方向上，從而使振動的峰值減小（如圖1所示）。

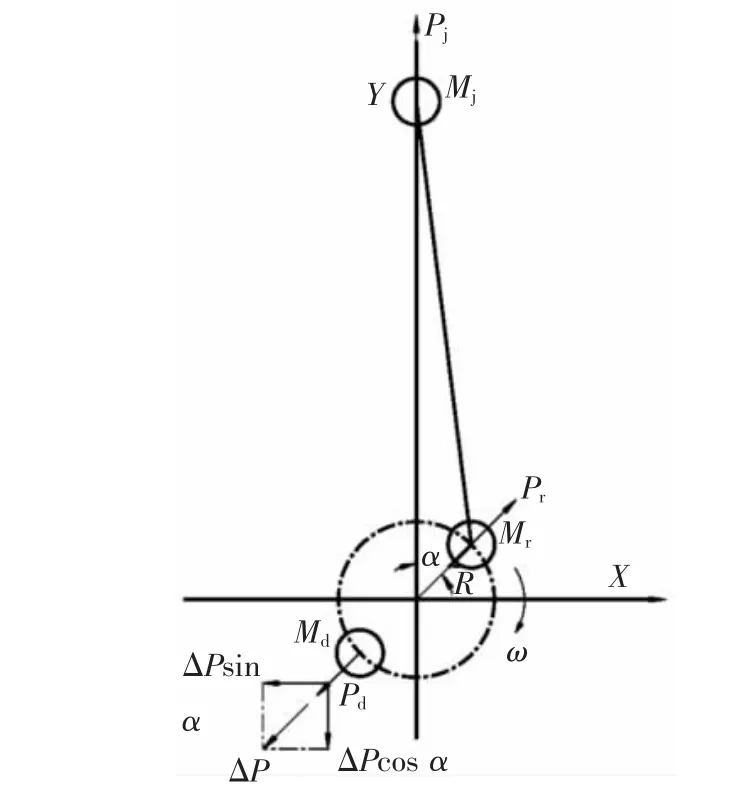
圖1 平衡機構示意圖

剩余離心力ΔP與一階往復慣性力Pj的合力在X、Y軸上的投影為：

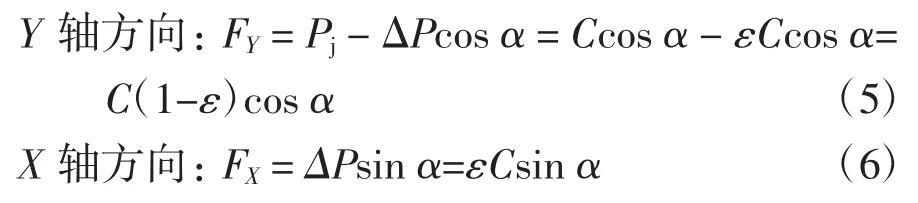
從上兩式中消去α得：

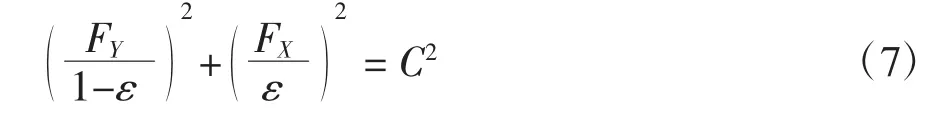
可知F矢量端軌跡是一個橢圓（如圖2所示）。

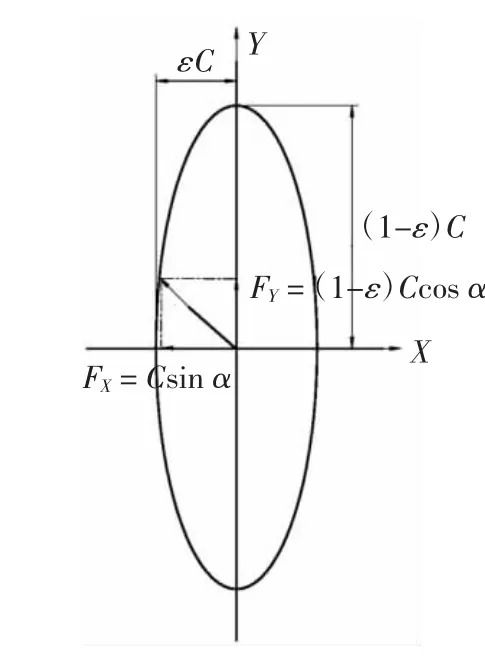
圖2 F矢量端軌跡

一般總是希望較大的慣性力，即橢圓的長軸方向，放在發動機剛度較大的方向或吸振能力較好的方向[2]。

2 某小型通用發動機動平衡計算

運用上述動平衡分析理論，通過電子秤和Pro/E軟件中的三維造型模型分析功能可知，活塞組質量mP＝204 g。連桿總重mL＝220.6 g，換算成大小頭質量后即大頭質量m2為139 g，小頭質量m1為80.6 g。曲柄銷質量mk＝279 g，擋圈質量mq＝2.6×2＝5.2 g（2個），滾針軸承質量mg＝45 g。

2.1 離心質量

離心質量產生的慣性力：

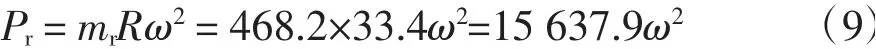
2.2 往復質量

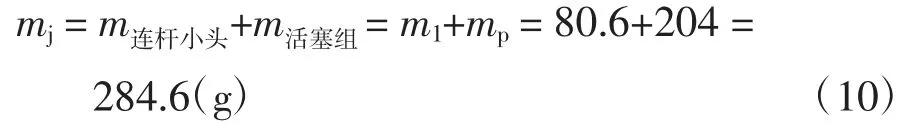
往復質量產生的慣性力：

2.3 平衡質量

運用Pro/E軟件中的模型分析功能

可求得平衡塊的質量和質心（如圖3所示）。

即md＝1394.5（g），質心坐標（X，Y）為（－1.4,－6.73），求得質心與曲柄旋轉中心距離：

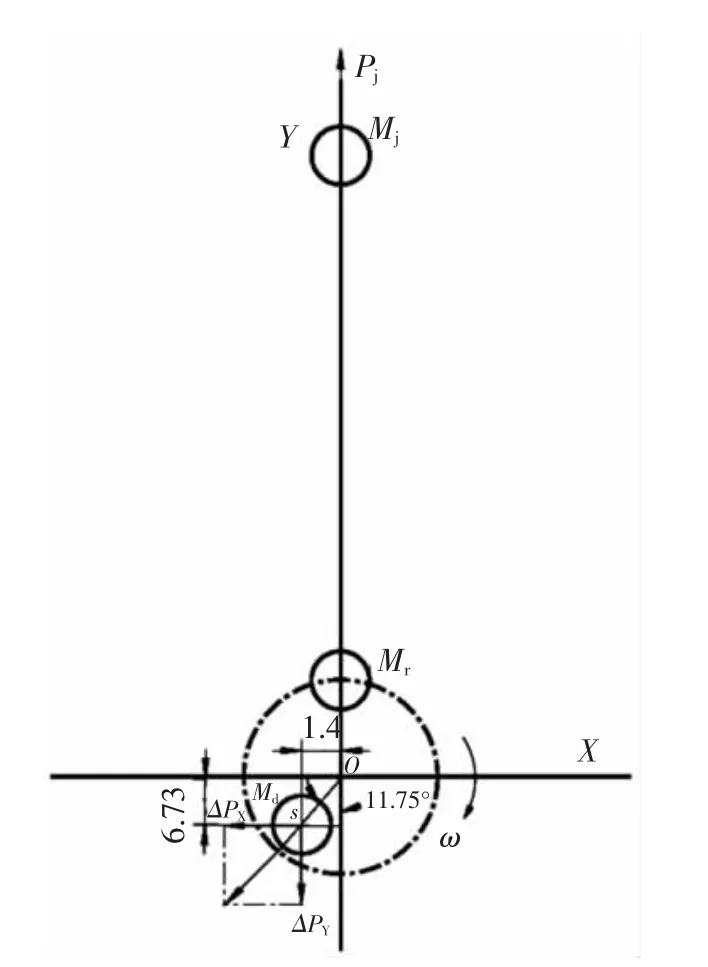
圖3 平衡塊的質量和質心（上止點位置時）

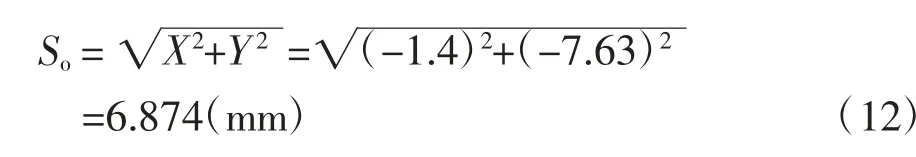
平衡質量產生的慣性力：

2 .4 動平衡分析

平衡質量產生的慣性力有兩種作用。一部分用來平衡離心慣性力Pr，另一部分用來平衡往復慣性力Pj。

平衡質量平衡了離心慣性力Pr后剩余的離心力投影（如圖4所示）。

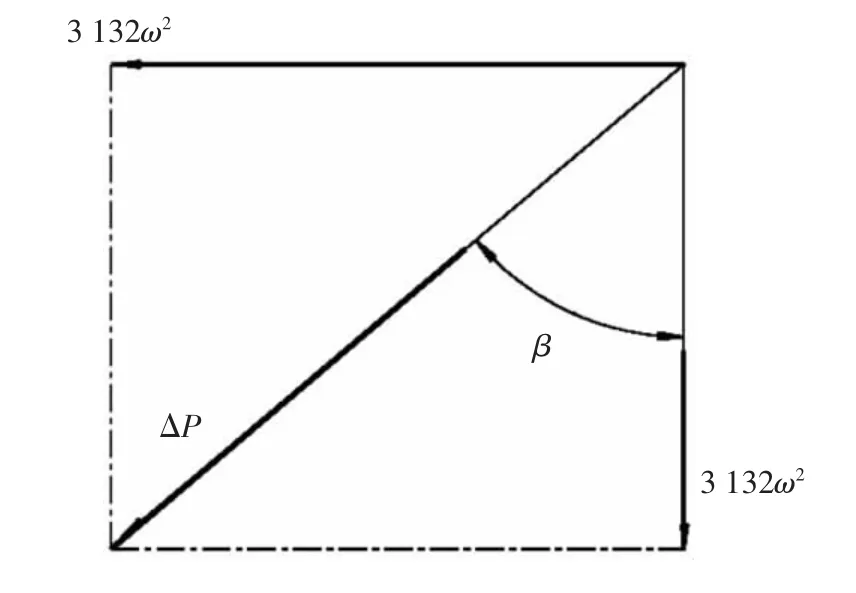
圖4 剩余離心力投影

在Y軸上：

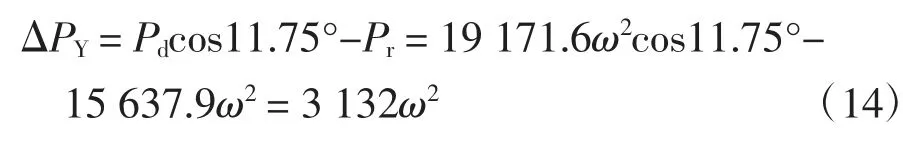
在X軸上：

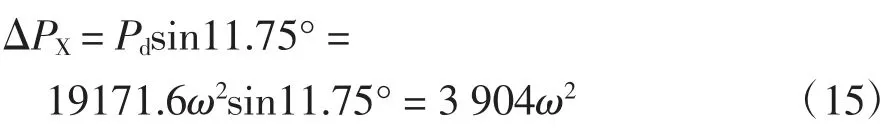
則剩余合力：

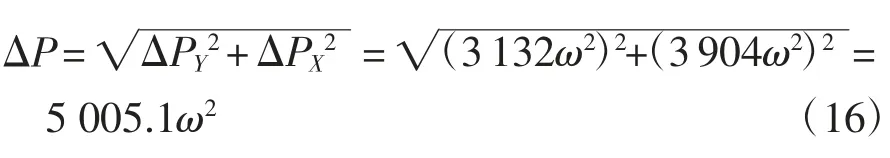
即平衡質量除平衡離心慣性力Pr外，還剩5 005.1ω2來平衡往復慣性力Pj，此剩余力與Y軸（氣缸中心線方向）夾角為51.2°。

此時，剩余離心力與往復慣性力Pj的合力F在X、Y軸方向的投影為：

α為曲軸轉角，取α為0°～360°CA之間的一系列值（如表1所示），可得出如圖5所示實際情況的一條橢圓曲線。可見某小型通用發動機慣性力橢圓是一個細長的扁扁的橢圓，其長軸與氣缸中心線夾角（Y軸）為31°左右，即發動機劇烈振動方向偏向氣缸中心線（Y軸）方向，而轉移到其它方向很小，所以造成整機明顯振動。

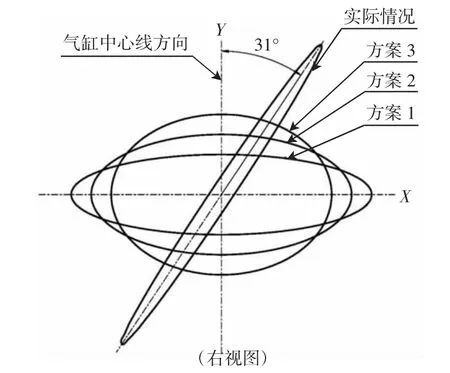
圖5 α為0°～360°CA時的橢圓曲線

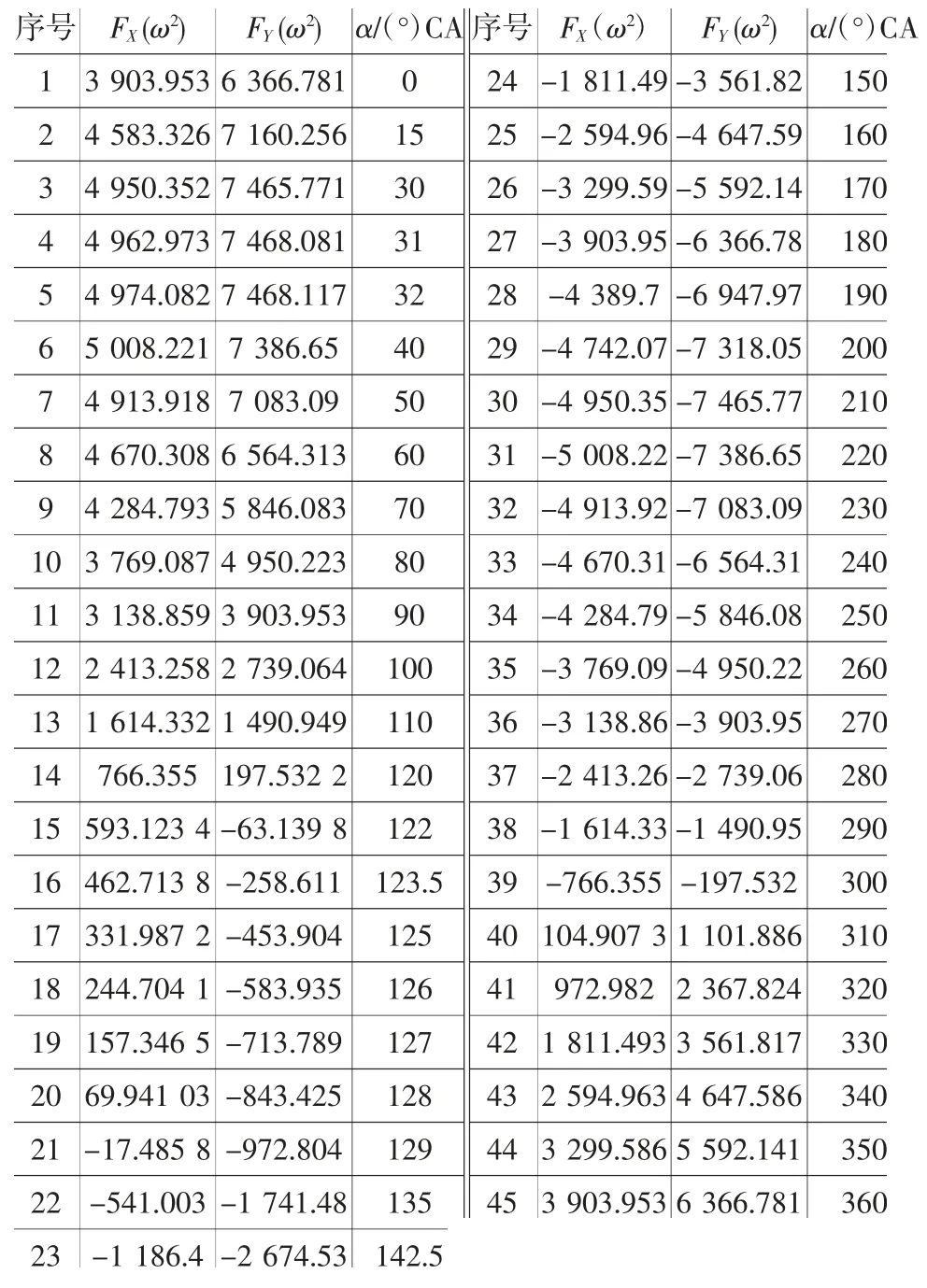
表1 α為0°～360°CA時的FX和FY值

3 改進方案及對策

一般總是希望橢圓的長軸方向（慣性力大的方向）放在發動機剛度較大的方向或吸振能力較好的方向。根據此原則再結合某小型通用發動機在整機上的布置，又考慮改進方案的經濟性[3]，可以采用在盡可能最少改變現有結構下的3種方案，其慣性力橢圓曲線如圖5所示。即希望把往復慣性力Pj由Y軸（氣缸中心線）轉移一部分至X軸（坐墊方向上）。X軸方向上的力可以通過整機上的減振彈性元件來克服，這樣可以大大減輕整機的振動，改善平順性和舒適性。至于轉移量的多少，可以通過實驗手段得出最佳值。

根據平衡質量離心力平衡掉旋轉質量的離心力Pr后與往復慣性力Pj的合力在X、Y軸上的投影公式（如圖2所示）：

Y軸方向：FY＝Pj－ΔP cosα＝9505.6ω2cosα－ΔP cosα

X軸方向：FX＝ΔP sinα

3.1 方案一

設ΔP＝2 000ω2

即FY＝9 505.6ω2cosα－2 000ω2cosα＝7505.6ω2cosα

FX＝2 000ω2sinα

可以得出如圖5所示的慣性力橢圓曲線，此時橢圓長軸方向（慣性力大的方向）已朝向X軸方向（坐墊方向），正是合理振動方向。

要ΔP＝2 000ω2，就必須對現有曲柄的平衡質量進行重新布置，通過Pro/E軟件的三維造型及模型分析功能，可以求出平衡質量。

3.2 方案二

同理設ΔP＝3 000ω2

即FY＝9505.6ω2cosα－3 000ω2cosα＝6505.6ω2cosα

FX＝3 000ω2sinα

3.3 方案三

同理設ΔP＝4 000ω2

即FY＝9 505.6ω2cosα－4 000ω2cosα

＝5 505.6ω2cosα

FX＝4 000ω2sinα

4 結論

1）對于小型通用發動機而言，由于結構的限制，采用轉移法來平衡一階往復慣性力雖然達不到完全平衡，但最大的優點是結構緊湊，經濟實用。

2）慣性力的大小對振動固然重要，但慣性力的方向和頻率在設計中也是需要重點考慮的因素。根據實驗結果[4]，方案三的措施最為有效，明顯地改善了振動，取得了令用戶滿意的效果。