密度泛函理論研究有機太陽能電池界面的激子分離及電荷轉移速率：DR3TBDT/PC60BM 體系

王冬梅， 田 軍,2， 鄭 茹， 柴 垚

(1.寶雞文理學院化學化工學院， 寶雞 721013; 2.岐山縣青化鎮初級中學， 寶雞 722402)

1 引 言

目前，最普通的硅太陽能電池能量轉換效率power conversion efficiency(PCE)已經達到～30%的理論值[1]， 然而高昂的生產成本阻礙了其廣泛的應用.而有機太陽能電池以其低廉的價格、環境友好、簡單的制作工藝等優勢在近些年吸引著廣泛的關注，并有望成為硅光伏的替代品.

有機太陽能電池器件通常具有三明治的夾心結構，即，給受體材料混合后被夾在兩個電極中間，其中陽極是透明的，透過太陽光.有機太陽能電池的光電轉換效率主要受以下五個步驟的控制[2, 3]：(1)活性材料吸收太陽光并產生激子(光吸收效率ηA)(2)激子擴散直到D/A界面(擴散效率ηD)，(3)激子在異質結界面處分離并伴隨電荷轉移態Charge transfer(CT)的產生(分離效率ηCS)，(4)電荷(空穴和電子)分別在給受體材料中傳輸并到達電極后富集(收集效率ηCC).在整個光致電荷產生的過程中，由(3)到(4)，電子和空穴也會發生重組(重組效率ηCR)又回到基態，因此，要提高器件的整體效率，ηA，ηD，ηCS和ηCC應該最大化，而ηCR應該最小化.然而，目前在有機太陽能電池中很難建立起過程中的每種效率與界面化學結構之間的關系，并且對于光伏活性材料的設計沒有簡單準則去校正能級并預測材料應有的加工過程.幸運的是，我們可以預測發生在電池中基本過程的速率.這些過程，如光吸收，激子形成以及電荷遷移，它們僅發生在異質結材料中而不包括界面.電荷分離(charge separation(CS))和電荷重組(charge recombination(CR))是兩個關鍵的界面過程，它們的競爭直接影響電池效率.預測這兩個過程的速率是估計界面電荷產生效率的第一步，從而指導新材料的設計.然而，估計這兩個過程的速率面臨最大的挑戰就是，它們的計算受到諸多因素的影響，如計算方法和模型的選擇等.盡管如此，我們在處理同一系列的分子時，選擇相同的計算方法和模型就可以定性地比較速率的大小趨勢，從而對材料進行篩選.

鑒于當前有機太陽能電池中光活性材料的理論研究大多數只停留在給受體材料的設計以及相關光譜性質的計算等方面，而有關給受體材料界面電荷轉移的理論研究相對較少且不成熟.電池效率方面，雖然最好的有機光伏器件效率已經超過10%[4]，但離商業化生產仍有一定的距離.為了進一步從材料分子的角度改善器件整體效率，本文以光伏活性材料中最具代表性的給體材料聚-3己基噻吩(P3HT)與受體材料苯基丁酸甲酯(PC60BM)組成的異質結體系[5-7]為參照，選取近期在實驗中合成的經典給體材料分子DR3TBDT，模擬該分子與經典受體材料PC60BM形成的DR3TBDT/PC60BM復合體系[8]，并以此為模型(圖1)，從動力學角度深入研究了給受體界面的電荷分離情況.在理論研究過程中，通過采用量子化學中的密度泛函理論方法，分別計算了孤立的給受體分子以及復合物的基態結構性質、吸收性質、激發態電荷轉移，并通過Rehm-Well表達式[9]，Marcus理論的雙勢阱[10]、雙球棍模型[11]以及廣義的Mulliken-Hush (GMH) 模型[12]分別計算了電子轉移和電荷重組過程中的Gibbs自由能變、內外重組能以及電子耦合，最后通過Marcus電荷轉移速率方程得出了界面的電荷轉移和重組速率，從而為新材料的設計從動力學角度提供理論表征手段.

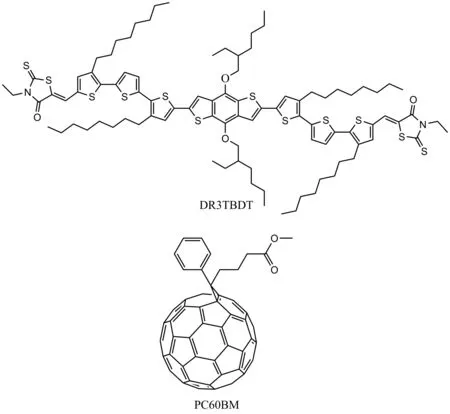
圖1 DR3TBDT和PC60BM的結構Fig.1 The structure of DR3TBDT and PC60BM

2 理論框架

2.1 計算細節

由于給受體間存在弱相互作用，DR3TBDT/PC60BM體系的基態構型優化采用了密度泛函理論中考慮了色散校正的ωB97X-D泛函和6-31G(d)基組，為保證計算結果的一致性，孤立的給受體分子DR3TBDT和PC60BM也采用相同的計算水平進行優化.所有分子的光譜吸收以及有關激發態的計算均采用含時密度泛函方法中的長程相關泛函CAM-B3LYP[13]和6-31G(d)基組[14]. Gibbs自由能、重組能和轉移積分的計算中，給受體分子相應態的能量計算均在B3LYP/6-31G(d)水平上完成.由于側鏈只是用來增加溶解性而不影響電子性質[15, 16]，因此為了節省機時，DR3TBDT中長的烷基鏈和烷氧基鏈都用H代替.所有計算都是在Gaussian09程序包中完成.此外，態密度圖、電荷差分密度圖均采用Mutiwfn 3.1程序完成.

2.2 界面模型

給受體分子之間最初的相對位置對復合物優化的結果以及界面電荷轉移和電荷重組速率常數的估計都有著顯著的影響.2009年，Bredas等人研究了并五苯/富勒烯體系給受體的兩種初始相對位置(并五苯平行或垂直于受體)對激子分離和電荷重組過程的影響[17].2011年，Alessandro等人研究了P3HT6/PC60BM體系給受體的八種初始相對位置[18]對界面電荷轉移和重組絕對速率的影響.研究表明，給受體初始不同位置對激子分離過程中的電子耦合影響最為顯著.在本文中，我們采用了最有利于分子間電子耦合的初始位置，即，PC60BM的兩個六邊形公用的棱與給體分子長軸方向所在的平面平行，如圖2所示，點a與b之間的初始距離為3.5 ?[19].從孤立分子到復合物，分子間的相互作用能可表示為：

△E=ED/A-(ED+EA)

(1)

式中，ED、EA和ED/A分別是給體、受體和復合物基態的能量.

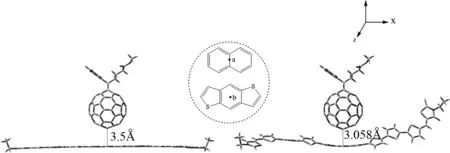
圖2 復合物DR3TBDT/PC60BM的初始構型(左)和優化后的構型(右)Fig. 2 The original model(left) and optimized(right) (ωB97XD/6-31G(d)) structure for DR3TBDT/PC60BM

2.3 Marcus速率方程

Marcus理論被廣泛地用于描述包括有機太陽能電池在內的給-受體體系的電荷轉移和電荷重組動力學[20].

(2)

式中，λ是重組能，VDA是給受體之間電子耦合，也叫電荷轉移積分.ΔG是電子轉移反應的吉布斯自由能變，kB是玻爾茲曼常數，h是普朗克常數，T是溫度(通常按300 K計算).通過計算λ、VDA和ΔG這三個參數就可以得到電荷轉移和重組速率常數.

3 結果與討論

3.1 基態性質

基于給定的模型，我們優化了復合物DR3TBDT/PC60BM，發現優化前后分子構型發生了明顯變化，給體分子由原來的平面構型變成兩端扭曲的結構，如圖2.根據式(1)，我們計算了孤立分子形成復合物的結合能，見表1.可以看出，它們之間的結合能在分子間作用力的范圍內(幾個千焦到幾十個千焦)，是一種弱相互作用[21].

表1 在ωB97X-D/6-31G(d)水平上計算的DR3TBDT, PC60BM和DR3TBDT/PC60BM的能級、穩定化能及結合能

Table 1 The calculated (ωB97XD/6-31G(d)) energy levels and stabilization energies of DR3TBDT, PC60BM and complex(DR3TBDT/PC60BM) as well as the binding energies between the isolate molecules and complex

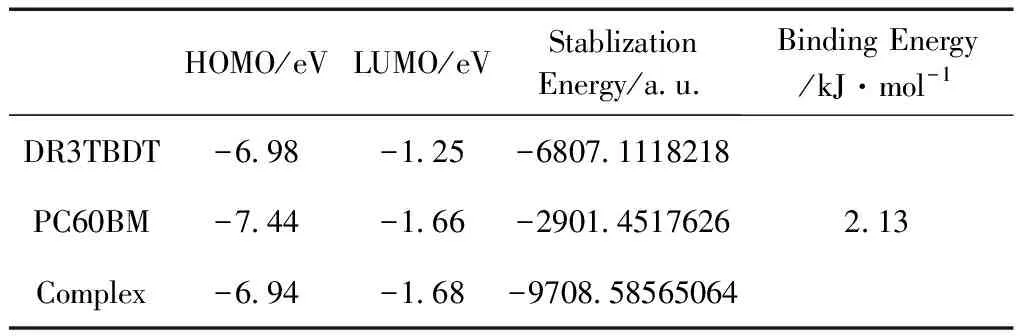
HOMO/eVLUMO/eVStablizationEnergy/a.u.Binding Energy/kJ·mol-1DR3TBDT-6.98-1.25-6807.1118218PC60BM-7.44-1.66-2901.4517626Complex-6.94-1.68-9708.585650642.13

注：表中HOMO為Highest Occupied Molecular Orbital的縮寫，LUMO為Lowest Unoccupied Molecular Orbital的縮寫.

此外，我們還計算了分子總的態密度density of states(DOS)和部分態密度partial density of states(PDOS)，如圖3所示.(a)和(b)圖分別是DR3TBDT的態密度圖，可以看出，側鏈C8H17和OC8H17對DR3TBDT分子軌道的貢獻很小，因此，通過簡化模型對后續工作的研究是可信的.(c)和(d)圖分別是DR3TBDT和PC60BM對復合物分子軌道貢獻的態密度圖.從圖中可以看出，對于復合物而言，電子密度在HOMO和LUMO的分布范圍為：-6.98～-7.02 eV(-0.258 a.u.～-0.062 a.u.)，對于DR3TBDT，電子密度在HOMO和LUMO 上的分布范圍為：-6.98～-1.25 eV(-0.257 a.u.～-0.046 a.u.)，對于PC60BM，電子密度在HOMO和LUMO上的分布范圍為：-7.44～-1.66 eV(-0.273 a.u.～-0.061 a.u.).從單個分子到復合物，HOMO上電子的貢獻主要來自給體，而LUMO主要來自受體.并且復合物的帶隙與孤立的給受體分子相比，下降了0.39-0.44 eV，這是給受體間電子耦合作用所致.能級如圖4所示.

3.2 光譜吸收和電子躍遷

所有分子光譜吸收過程中的主要的電子躍遷、振子強度和軌道貢獻均列于表2、3中，模擬的吸收曲線見圖5.結合表2和圖5(a)可以看出，DR3TBDT有三個吸收峰，最大吸收峰在451 nm處，主要來自HOMO(H)→LUMO(L)和H-1→L+1的S0→S1躍遷，另外兩個肩峰在430～370 nm附近，分別來H-1→L和H→L+1的S0→S2躍遷以及H→L+2的S0→S5躍遷.從表3和圖5(b)可知，PC60BM的強吸收主要集中在紫外區250-300 nm處，主要來自電子躍遷S0→S26，S0→S34，S0→S35，S0→S36以及S0→S46.并且第一激發態對應的513 nm為弱吸收.計算的50個態的電子躍遷和振子強度列于表3.由表3和圖5(c)可知，DR3TBDT/PC60BM的最大吸收峰在502 nm處，為S0→S1的躍遷，最強的吸收峰位于449 nm處，為S0→S6的躍遷，最強吸收峰的位置和曲線的形狀與圖5(a)相似，這說明復合物對太陽光的吸收主要來自給體分子.

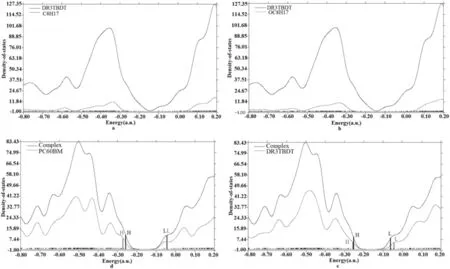
圖3 DR3TBDT和DR3TBDT/PC60BM的態密度(DOS)圖Fig. 3 Partialdensities of state (PDOSs) for DR3TBDT and complex(DR3TBDT/PC60BM)

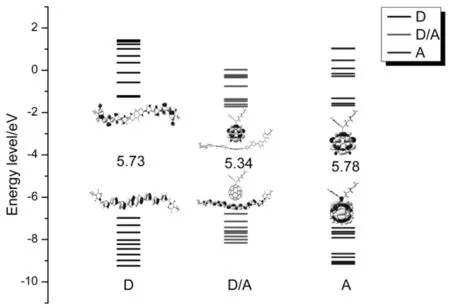
圖4 在ωB97X-D/6-31G(d)水平上計算的DR3TBDT(D), PC60BM(A) 和DR3TBDT/PC60BM(D/A)的前線分子軌道能級Fig. 4 The frontier molecular orbital energy levels for DR3TBDT(D), PC60BM(A) and Complex(D/A)

表2 在C-PCM(CHCl3)-CAM-B3LYP/6-31G(d)水平上計算的DR3TBDT躍遷能(eV, nm)，振子強度(f)和軌道貢獻

Table 2 The calculated(C-PCM(CHCl3)-CAM-B3LYP/6-31G(d)) transition energies(eV, nm)，oscillator strengths(f) and orbital contributions for DR3TBDT

E/eV(nm)fOrbital contributionsS12.7487(451.1)4.2659HOMO-1→LUMO+1(31%), HOMO→LUMO (39%)S22.8514(434.8)0.1980HOMO-1→LUMO(41%), HOMO→LUMO+1 (31%)S53.3232(373.1)0.7000HOMO→LUMO+2 (47%)

3.3 激發態電荷轉移

為了清楚地闡明從基態到激發態的電荷轉移以及激發態的電荷分布，我們繪制了孤立分子和復合物分子基于S0→Sn躍遷的電荷密度差分圖charge density difference(CDD)并計算了電荷轉移(CT)參數(DCT,qCT和μCT)，如表4所示.其中，DCT是激發過程中電子密度增加的區域和密度減小的區域的重心距離，qCT是電荷轉移數目，μCT是變化的偶極距.可以看出DR3TBDT在從S0分別到S1和S2時，電子密度變化發生在整個分子骨架上，從電荷轉移參數值看，S1和S2相差不大，說明它們有相似的電荷轉移特征.而S0到S5躍遷時，

表3 在C-PCM(CHCl3)-CAM-B3LYP/6-31G(d)水平上計算的PC60BM和復合物DR3TBDT/PC60BM(D/A)的躍遷能(eV, nm)及振子強度(f)

Table 3 The calculated(C-PCM(CHCl3)-CAM-B3LYP/6-31G(d)) transition energies(eV, nm) and oscillator strengths(f) for PC60BM and Complex

PC60BME/eV(nm)fComplexE/eV(nm)fS12.4145(513.5)0.00392.4654(502.8)0.0030S22.4467(506.8)0.00002.5035(495.2)0.0000S32.5289(490.3)0.00002.5880(479.0)0.0000S42.5475(486.7)0.00002.5970(477.4)0.0000S52.6774(463.1)0.00032.7397(452.5)0.0003S62.7242(455.1)0.00052.7576(449.6)4.1894S72.7850(445.2)0.00002.7792(446.1)0.0011S82.8280(438.4)0.00002.8386(436.8)0.0719S92.8702(431.9)0.00162.8403(436.5)0.0313S102.9555(419.5)0.00232.8633(433.0)0.0006S112.9723(417.1)0.00222.8849(429.7)0.0016S122.9958(413.9)0.00003.0105(411.8)0.0024S133.0876(401.6)0.00013.0489(406.6)0.0005S143.1388(395.0)0.00383.0710(403.7)0.0000S153.1803(389.9)0.01983.0886(401.4)0.0021S163.4683(357.4)0.00363.1390(394.9)0.0059S173.5126(352.9)0.00003.1770(390.2)0.0008S183.5485(349.4)0.00223.2016(387.2)0.0104S193.7122(333.9)0.00663.2238(384.5)0.0016S203.7223(333.0)0.01823.3153(373.9)0.1824S213.7266(332.7)0.0008S223.7890(327.2)0.0025S233.8057(325.7)0.0000S243.8679(320.5)0.0183S253.9027(317.6)0.0002S264.0291(307.7)0.1924S274.0732(304.3)0.0379S284.1200(300.9)0.0057S294.1503(298.7)0.0047S304.1680(297.4)0.0542S314.1950(295.5)0.0004S324.2451(292.0)0.0117S334.2544(291.4)0.0301S344.3315(286.2)0.5654S354.3498(285.0)0.1143S364.3724(283.5)0.2183S374.3951(282.0)0.0133續表3S384.4271(280.0)0.0313S394.4293(279.9)0.0017S404.4997(275.5)0.0861S414.5145(274.6)0.0024

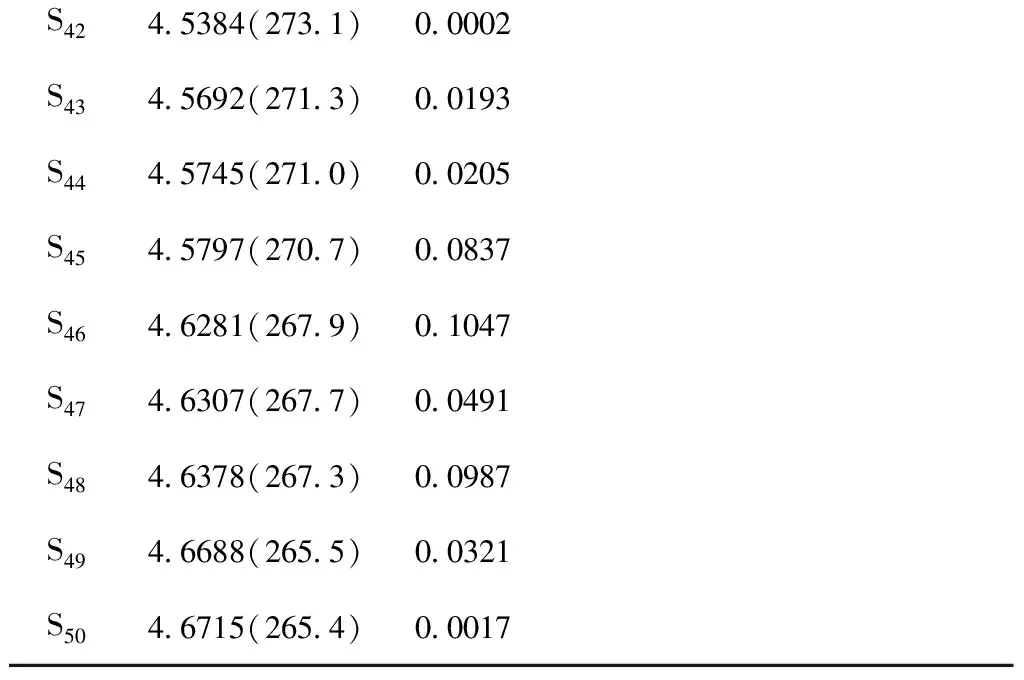
S424.5384(273.1)0.0002S434.5692(271.3)0.0193S444.5745(271.0)0.0205S454.5797(270.7)0.0837S464.6281(267.9)0.1047S474.6307(267.7)0.0491S484.6378(267.3)0.0987S494.6688(265.5)0.0321S504.6715(265.4)0.0017

電荷只集中在了一側的橋和端基上，在中心給體核和另一側幾乎沒有分布.從電荷轉移數目來看，從基態到S1、S2和S5很接近，然而隨著激發態能級的增加，qCT和μCT都呈現增加的趨勢，尤其是S5態的μCT為10.211，說明高激發態下，正負電荷極易發生分離，電子很容易易從DR3TBDT的LUMO轉移到PC60BM的LUMO上.而對于孤立的PC60BM，S1態時電荷轉移數目最多，而其它幾個高能激發態的qCT比較接近，且C60上電荷分布明顯減少.S1和S35電荷類似地分布在C60上，而S26，S36，S46電荷在取代基苯環上呈現較多的分布，同時電荷由苯環向C60轉移.此外，隨著激發態能級的增加，qCT和μCT大致呈增加的趨勢，這與線性給體分子中的電荷分布非常相似，即，高激態下激子易解離.對于復合物分子而言，S1和S2呈現明顯的電荷轉移特征，但是空穴和電子并沒有完全地分別分布在給體和受體上，所以S1和S2是分子間電荷轉移激發態.

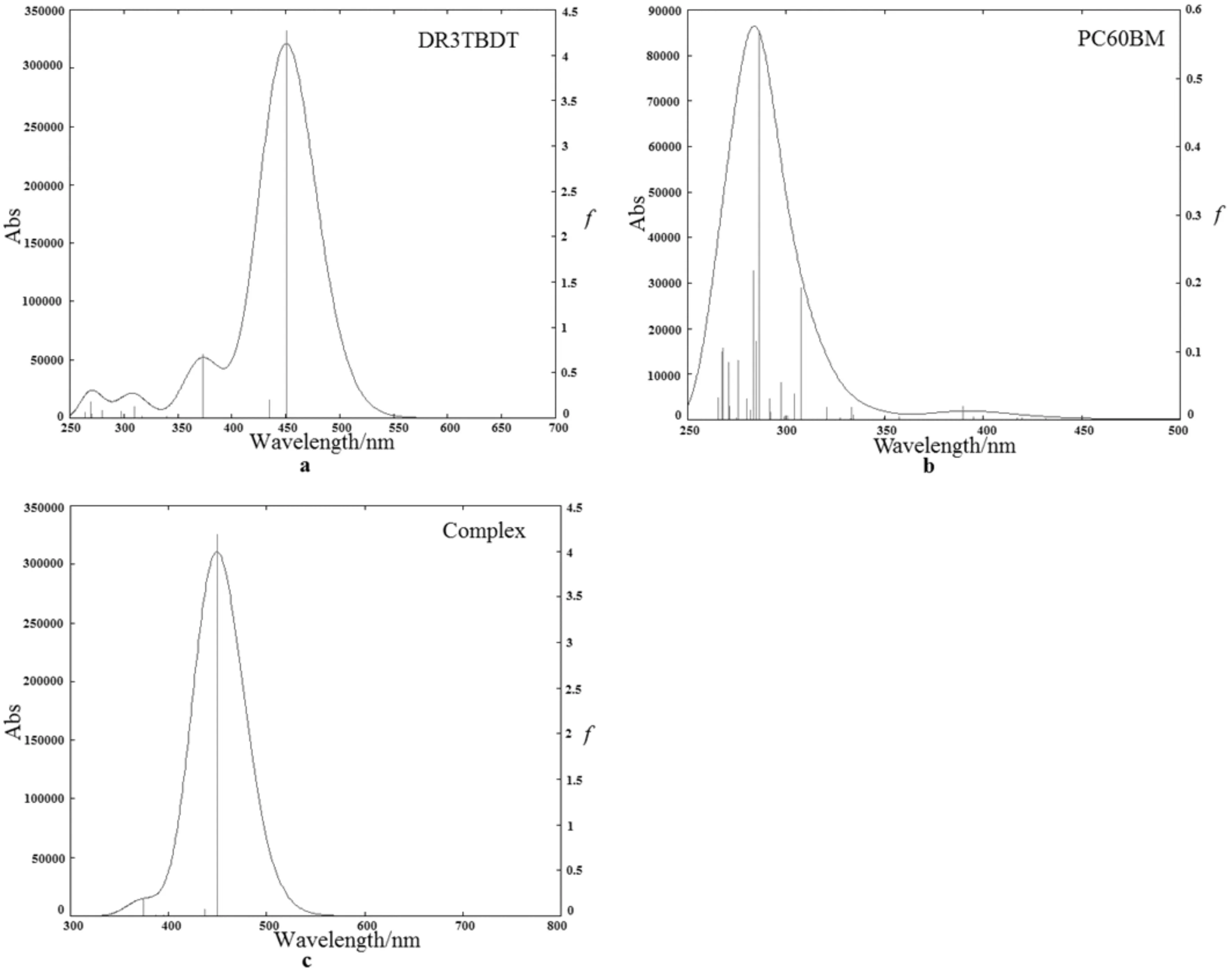
圖5 在C-PCM(CHCl3)-CAM-B3LYP/6-31G(d)水平上模擬的DR3TBDT(a)、PC60BM(b)和DR3TBDT/PC60BM(c)的高斯吸收曲線Fig.5 The simulited(C-PCM(CHCl3)-CAM-B3LYP/6-31G(d)) spectra absorption curves of DR3TBDT, PC60BM and Complex

為了獲得有效的電荷轉移和減緩電荷重組，根據Marcus理論，電荷轉移過程中給受體間電子耦合應該最大化，重組能應該最小化.通過計算電荷轉移和重組這兩個過程中的吉布斯自由能變、重組能以及電子耦合，就可以得到相應速率.

3.4 Gibbs自由能

在激子分離和電荷重組過程中，ΔG分別表示為ΔGCT和ΔGCR.它們的計算可以通過兩種方法：一是孤立組分的中性/激發態和陽離子/陰離子態與庫侖引力項ΔEC的加和[9]，也稱為Rehm-Well表達式；另一種方法是分別計算D/A復合物在DA、D*A和D+A-態的能量而求得[18].這兩種方式中能量都是通過相應的平衡態構型獲得.第一種方法忽略了相互極化效應.第二種方法考慮了極化效應但是需要優化D/A復合物的激發態構型.值得注意的是，不能把ΔGCT簡單看作是給受體的LUMO能差，這樣會過高估計CT激子的能量.在本文中采用第一種方法來計算ΔGCT和ΔGCR.即：

ΔGCT=E(D+)+E(A-)-E(D*)-E(A)+ΔEC

ΔGCR=E(D)+E(A)-E(D+)-E(A-)+ΔEC

(3)

在吉布斯自由能的計算中，qA和qD分別為給受體相應態的Mulliken電荷，εs是周圍溶劑的介電常數，實驗中為氯仿(4.80).根據公式(2)，可以分別得到ΔGCT和ΔGCR，如表5所示.

3.5 重組能

重組能通常分為內重組能(分子在電子得失過程中幾何構型發生變化所引起的)和外重組能(電荷轉移過程中周圍環境所引起的).內重組能通常采用雙勢阱模型計算(也稱四點法，如圖7)[22, 23]，用λi表示.

(4)

(5)

圖3描述的是D*A和D+A-兩個勢能面，上述公式中能量E的上標代表反應物所在的態，下標表示態所在的平衡幾何構型.

外重組能的精確計算比較復雜.通常使用的是基于Marcus雙球棍模型的連續介質模型[11].

表4 DR3TBDT、PC60BM和DR3TBDT/PC60BM基于S0→Sn的電荷密度差分圖以及激發態電荷轉移數目(qCT/|e-|)、距離(DCT/ ?)和偶極距(μCT/ Debye)，紫色和藍色分別表示電子密度的增加和減少

Table 4 Plotted electronic density difference maps and computed charge transfer distances, amounts and dipoles (DCT,qCTandμCTin ? ,|e-|and Debye, respectively) between S0and Snof all the molecules at the B3LYP/6-31G(d) level. Blue and purple colors correspond to a decrease and increase of electron density, respectively.

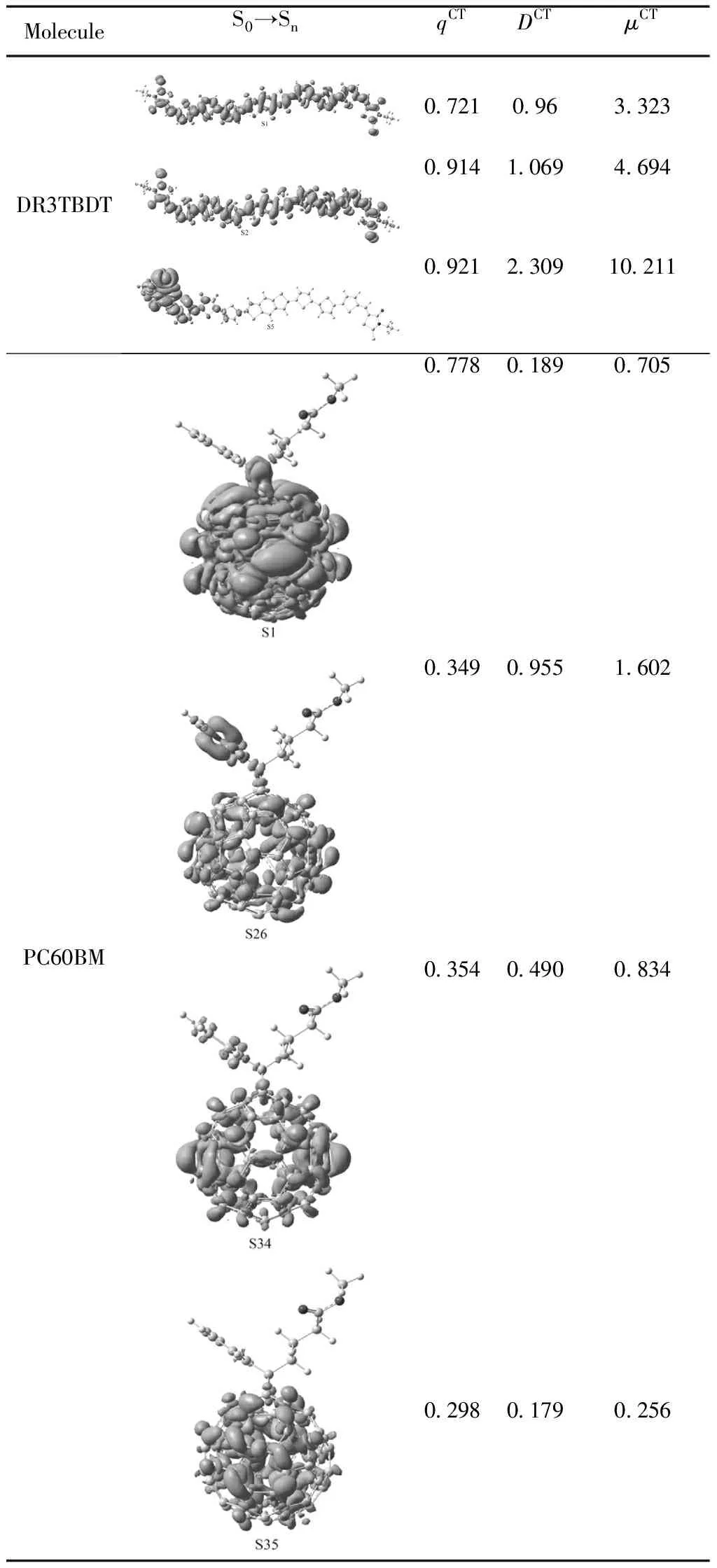
MoleculeS0→SnqCTDCTμCTDR3TBDT0.7210.963.3230.9141.0694.6940.9212.30910.211PC60BM0.7780.1890.7050.3490.9551.6020.3540.4900.8340.2980.1790.256

PC60BM0.3501.4492.4350.3951.6513.129DR3TBDT/PC60BM1.4143.12721.2341.4023.09120.8110.5340.2660.6830.4540.3860.8410.5790.1220.3400.4630.0720.1590.4940.5341.266

(6)

式中，dD、dA和dDA分別是給受體半徑和給受體的質心距離.εop和εo分別是周圍環境的光學介電常數和真空介電常數.

在重組能的計算中[24, 25]，我們采用經典的勢能面曲線法計算了內重組能，即公式(4)，而對于外重組能的計算，涉及到給受體半徑和周圍溶劑的介電常數.通常把給受體分子看成是帶電的球形電荷，采用Gaussian 09中的PCM模型先計算出分子球的體積，從而得到分子半徑.根據公式(5)，可得外重組能.值得注意的是，電子轉移和電荷重組在氯仿溶劑中幾乎是同時進行的，所以在計算重組能的時候，需要將每個過程中的內重組能分別與外重組能進行加和.如表6所示.

表5 B3LYP/6-31G*水平上與Gibbs自由能有關的參數

表6 B3LYP/6-31G*水平上與重組能有關的參數

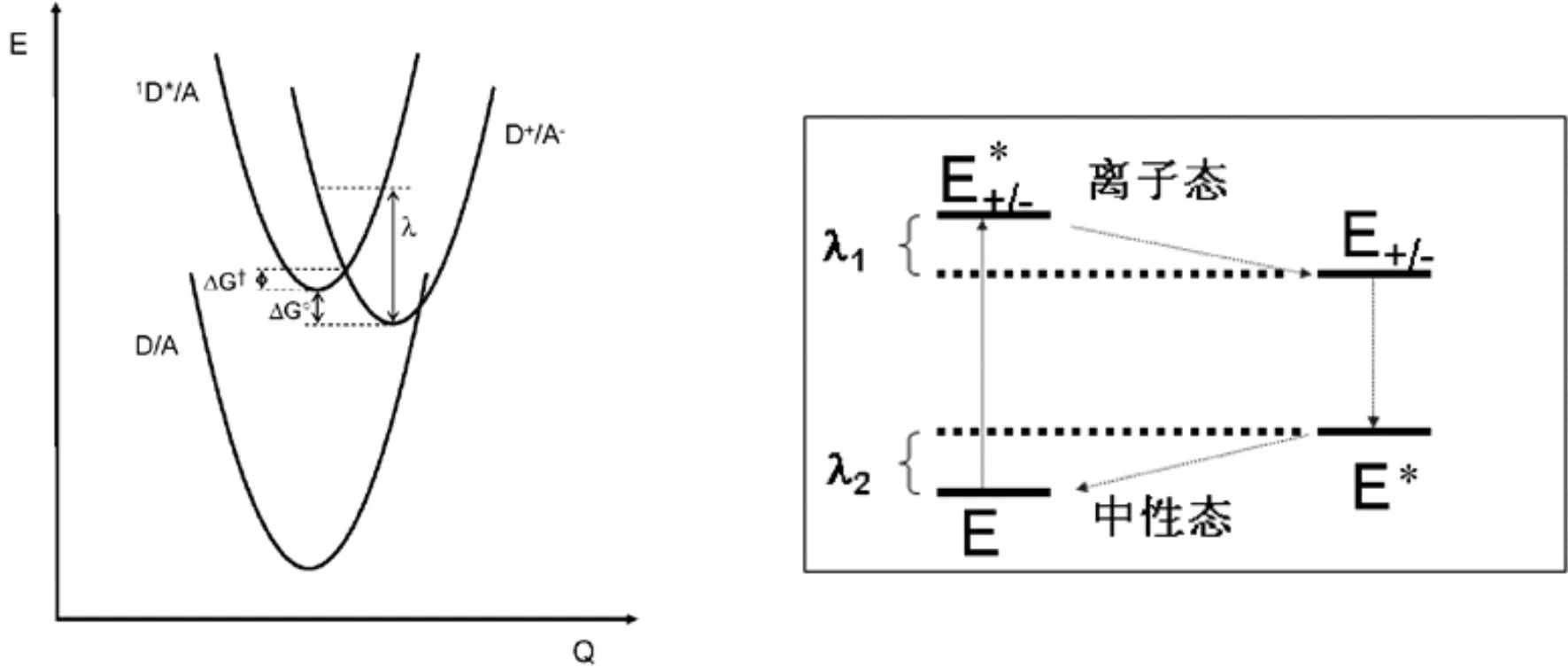
圖6 雙勢阱模型下的內重組能計算方法Fig. 6 Calculation method of internal recombination energy in double-well model

3.6 電子耦合

與重組能的計算相比，目前電子耦合還沒有一個完全精確的估計方法，在本文中，我們采用近似的廣義Mulliken-Hush(GMH)模型[26, 27]來計算激發態的電荷轉移積分，(電子轉移耦合矩陣元)，這被Sun等人證實很適合我們研究的體系[12].轉移積分在兩態公式中(S0和Sn態)可表示為：

(7)

式中，μtr是復合物Sn態沿Y軸方向的躍遷偶極距，Δμ是兩態的偶極距差，ΔE是垂直激發能.

根據激發態電荷轉移的結果，S1和S2是分子間電荷轉移激發態，即電子和空穴不完全分布在給體或者受體分子上，所以S1和S2是兩個簡并的分子間電荷轉移激發態.VDA的值等于VDA(S1←S0)和VDA(S2←S0)的加和，表7中的數據結合計算的第一垂直激發能Es1和第二垂直激發能Es2帶入根據公式(2)可以得到VDA=55.5 meV.

表7 DR3TBDT/PC60BM基于S0、S1和S2的偶極距以及S0→S1和S0→S2的躍遷偶極距 (單位: Debye)

Table 7 The diploe moments for S0, S1and S2as well as the transition dipole moments for S0→S1(unit: Debye)

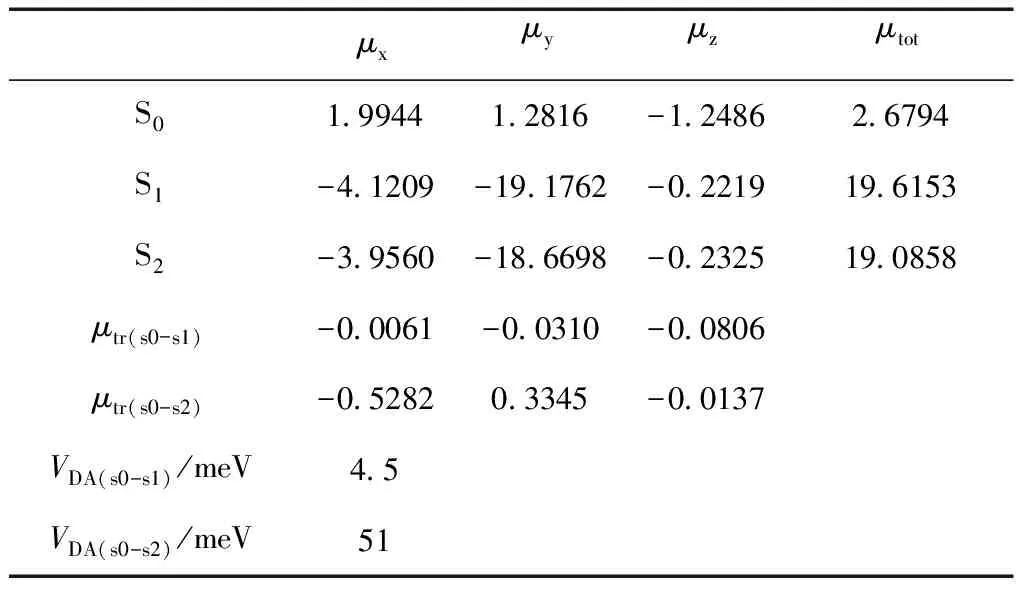
μxμyμzμtotS01.99441.2816-1.24862.6794S1-4.1209-19.1762-0.221919.6153S2-3.9560-18.6698-0.232519.0858μtr(s0-s1)-0.0061-0.0310-0.0806μtr(s0-s2)-0.52820.3345-0.0137VDA(s0-s1)/meV4.5VDA(s0-s2) /meV51

3.7 電荷轉移和重組速率

將得到的Gibbs自由能、重組能以及轉移積分分別代入方程(1)，計算得到的電荷轉移和電荷重組速率分別為：kCT= 7.2×1011s-1；kCR= 9.8×1010s-1.與實驗中測得的速率范圍非常吻合.

4 結 論

本文以實驗報道的DR3TBDT/PC60BM體系為模型，在研究孤立給受體分子和復合物的基態和激發態性質的基礎上，進一步研究了界面的激子分離和電荷重組.Gibbs自由能通過Rehm-Well表達式求得，重組能分別通過Marcus理論的雙勢阱和雙球棍模型求得，轉移積分通過廣義的Mulliken-Hush模型近似求得，在此基礎上根據Marcus電荷轉移方程得到了該體系的電荷轉移速率和重組速率分別為kCT= 7.2×1011s-1；kCR= 9.8×1010s-1.