里德里原子偶極阻塞效應的平均場的研究

毛如圣， 張 波， 劉子龍， 楊 波

(武漢理工大學理學院物理系， 武漢 430070)

1 引 言

里德堡原子是指原子最外層電子被激發到主量子數n很大的高激發態原子[1]，它具有自發輻射壽命長、極化率大和電偶極矩強等特殊的物理性質[2]. 里德堡原子對外部電磁場十分敏感，不僅可以利用其對外場進行探測，還可以利用外場實現對里德堡原子的操控[3～6]. 隨著激光冷卻技術的發展，超冷里德堡原子的獲得使多普勒效應得到有效的抑制，推進了里德堡原子間相互作用的研究與應用[7]. 里德堡原子之間的相互作用大致可分為兩類[8]：一類為長程范德瓦爾斯相互作用，其相互作用能為Vint=-C6/R6；另一類稱為偶極-偶極相互作用，其相互作用能為Vint∝1/R3，且這種相互作用比范德瓦爾斯相互作用更強. 里德堡原子之間的相互作用導致里德堡能級頻移，從而在里德堡原子周圍一定距離內的其他原子無法被激發到里德堡態，這個現象被稱為偶極阻塞效應[9,10]，這個距離為偶極阻塞半徑[11]. 利用里德堡原子的相互作用與偶極阻塞效應可以實現量子比特、量子邏輯門以及量子糾纏態的制備[12～16]，這是量子信息處理[17]的基礎量子計算[18]的關鍵. 約化密度矩陣法[19]和量子蒙特卡羅[20, 21]等方法已被用于計算和模擬里德堡原子間的相互作用和偶極阻塞效應. 本文利用平均場法[22]計算里德堡原子的偶極阻塞效應，在主量子數和原子密度不大的條件下[23]，計算過程較前述兩種方法簡單，里德堡原子間的相互作用的影響可以得到簡化，同時本文還分析了主量子數、拉比頻率與原子密度對偶極阻塞效應的影響.

2 平均場模型

對于一個存在相互作用的多原子系統，其每一個原子都將受到周圍原子的影響. 將其周圍原子的相互作用進行迭加，并根據原子密度分布進行平均，從而可以形成一個只依賴于此原子的平均勢場，這個平均勢場可用一個單體算符來描述. 即利用平均場法，可以將單個原子受到相互作用力用一個算符來表達.

(1)

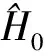
(2)

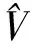
(3)

其中ri與rj分別表示第i和j個原子的位矢，C6為里德堡原子間的相互作用系數[26]，利用朗道平均場理論，忽略場的二階漲落，即(|e〉i〈e|-ρee)(|e〉j〈e|-ρee)≈0，這里ρee為原子處于里德堡態的幾率，可以得到：

|e〉i〈e||e〉j〈e|≈|e〉i〈e|ρee+

(4)

其中第二步將第i和j個原子當做等價的來處理.

當原子數較多時，可以將原子看作是準連續的，于是求和符號化為積分[27]. 當兩原子之間的距離r=ri-rj遠小于偶極阻塞半徑Rd即r<>Rd時，兩個原子均可以被激發為里德堡原子. 因此：

(5)

再將(4)和(5)式代入到(3)式中，在忽略不影響密度矩陣運動方程的常數項后，可以求得相互作用哈密頓量的表達式：

(6)

3 速率方程

由主量子方程：

(7)

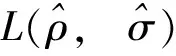
(8)

(9)

(10)

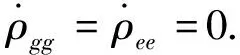
(11)

4 結果與分析討論

4.1 偶極阻塞效應對原子躍遷的影響

取銣原子團的密度為ρ=3×1010cm-3，激光場拉比頻率為Ω=5 MHz、自發輻射概率為Γ=6 MHz、激光線寬為γ=2 MHz，我們計算了不同頻率失諧量下，銣原子團被激發到n=50的里德堡態的幾率，如圖1所示. 圖中黑色實線是不考慮原子間偶極相互作用(即公式(9)中Δint=0)時，原子的激發幾率；紅色虛線是考慮原子間偶極相互作用(Δint≠0)時，原子的激發幾率.

如果不斷減小銣原子團的密度，原子間偶極相互作用會隨之不斷減小，以至圖中兩條曲線重合. 在不考慮原子間偶極相互作用且激光頻率失諧量Δ=0時，得到最大的激發幾率，此時被激發到里德堡態的原子占比約為22.73%(見圖1中黑色實線). 在ρ=3×1010cm-3時，原子間偶極相互作用不為0(Δint≠0)不可忽略，紅色虛線是加上原子間偶極相互作用后，里德堡原子的占比. 原子間偶極相互作用使里德堡能級發生頻移，此時只有當激光頻率失諧量Δ與里德堡能級頻移Δint之和為0時，才能得到最大激發幾率，僅為19.32%(見圖1中紅色虛線)這是因為偶極阻塞效應導致處于阻塞半徑內的原子無法被激發到里德堡態.

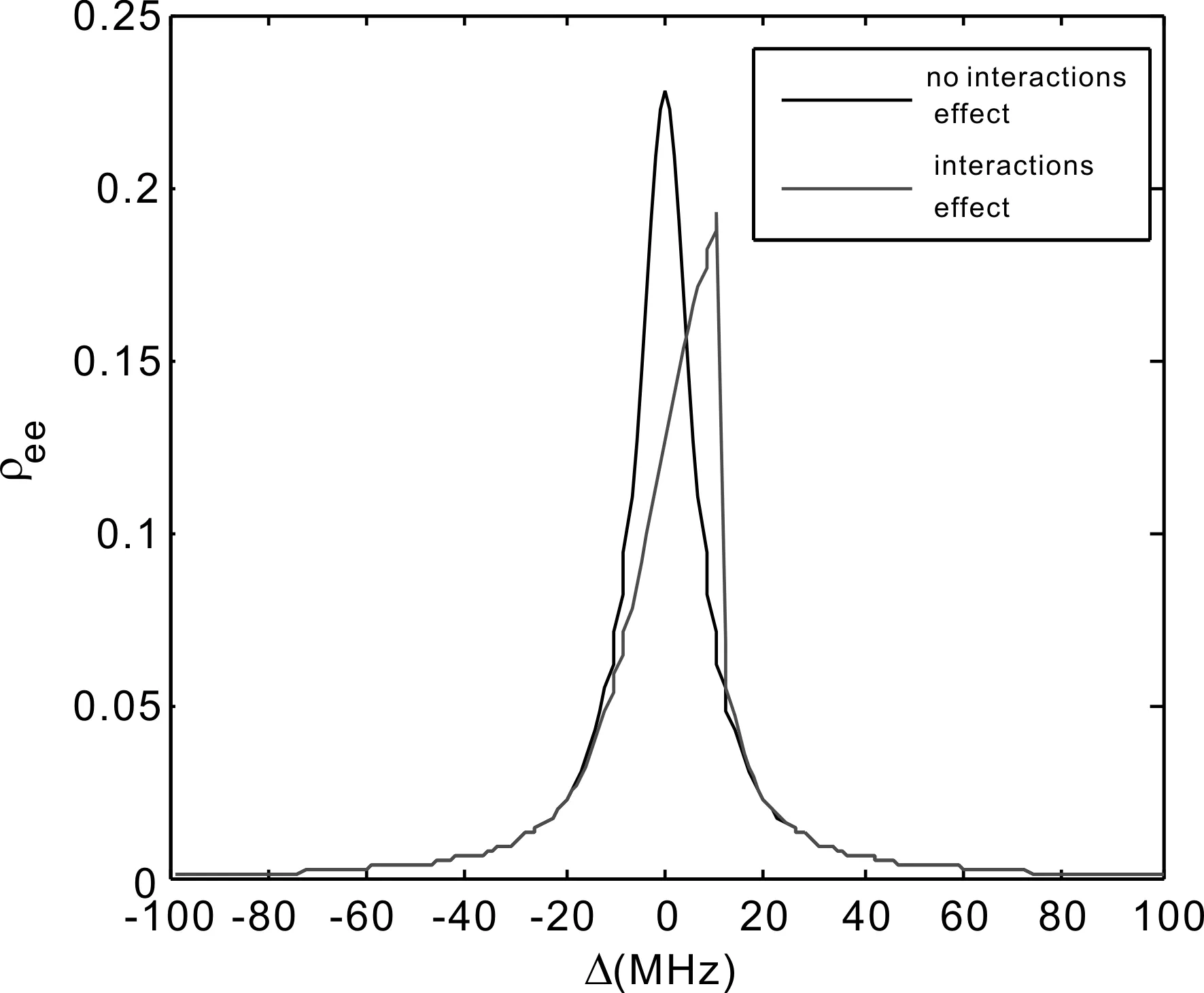
圖1 里德堡原子占比Fig.1 Population of excited Rydberg atoms vs laser detuning

4.2 主量子數對偶極阻塞效應的影響

被激發到不同主量子數的里德堡原子之間的相互作用大小不同，所導致的偶極阻塞效應也不同. 對于密度為ρ=3×1010cm-3的銣原子團，拉比頻率為Ω=5 MHz、自發輻射概率為Γ=6 MHz、激光線寬為γ=2 MHz，且滿足Δ+Δint=0時，我們計算了主量子數n從50到80時，里德堡原子的激發幾率，如圖2所示. 這里所選取原子團的密度較小，原子間的相互作用相對較弱，在n=80時，仍可用平均場法來近似計算.

隨著主量子數的增大，里德堡原子的躍遷偶極矩急劇增大，里德堡原子間的相互作用力也隨之增大，導致里德堡能級頻移增大，偶極阻塞效應強烈，抑制基態原子向里德堡態的躍遷. 從而在圖2的曲線可以看出，主量子數的越大，被激發到里德堡態的原子數目越少. 當主量子數n=50時，被激發到里德堡態的原子占比約為19.32%，而當主量子數n=80時，被激發到里德堡態的原子僅占了2.44%. 即隨著主量子數的增大，里德堡原子的偶極阻塞效應越明顯.

圖2 不同主量子數時里德堡原子的激發幾率Fig.2 population of excited Rydberg atoms at different principal quantumnumbers

4.3 拉比頻率對偶極阻塞效應的影響

激光功率將會影響里德堡原子的偶極阻塞效應，而激光功率越大對應的拉比頻率也就越大. 對于密度為ρ=3×1010cm-3的銣原子團，其自發輻射概率為Γ=6 MHz、激光線寬為γ=2 MHz，滿足Δ+Δint=0時，我們計算了拉比頻率Ω從0 MHz到20 MHz時，被激發到n=50的里德堡態原子占比，如圖3所示.

當拉比頻率小于5 MHz ，隨著拉比頻率的增加，被激發到里德堡態的原子數目線性增大，這是因為拉比頻率較小時，被激發到里德堡態的原子數很少，處于偶極阻塞半徑內的原子也較少，大部分原子的里德堡能級不會有顯著變化，不會出現偶極阻塞效應；當拉比頻率大于5 MHz，隨著拉比頻率的增大，里德堡原子數目逐漸增加，處于偶極阻塞半徑內的原子增多，大部分原子的里德堡能級也都發生明顯頻移，導致偶極阻塞效應增強；當拉比頻率足夠大(約大于15 MHz)時，被激發到里德堡的原子數目達到飽和，大部分原子都處于偶極阻塞半徑內，原子無法被激發到里德堡態，從而有十分明顯的偶極阻塞效應.

圖3 不同拉比頻率時的里德堡原子的激發幾率Fig. 3 population of excited Rydberg atoms at different Rabi frequencies

4.4 原子密度對偶極阻塞效應的影響

同樣原子密度也將影響偶極阻塞效應，原子的密度越大則原子間的間距越小. 當拉比頻率為Ω=5 MHz、自發輻射概率為Γ=6 MHz、激光線寬為γ=2 MHz，滿足共振條件Δ+Δint=0時，我們計算了原子間距a從10-7m逐漸增大到的10-5m時(對應密度從1015cm-3變化到109cm-3)，被激發到n=50的里德堡態原子占比，如圖4所示. 主量子數為n=50，在所取密度范圍內(109cm-3～1015cm-3)，原子間的相互作用較弱，仍可以用平均場法來近似.

當原子的間距a遠小于偶極阻塞半徑Rd時，原子將會受到強大偶極相互作用，所有的基態原子均無法被激發到里德堡態，偶極阻塞效應明顯；當原子團密度降低時，原子間距a也逐漸增大，原子間的偶極相互作用隨之降低，部分原子處于偶極阻塞半徑之外，從而這些基態原子能夠被激發到里德堡態，處于里德堡態的原子數目也逐漸增加，偶極阻塞效應減弱；當原子間距a足夠大時，原子之間的偶極相互作用力非常弱，此時里德堡原子占比為一定值，偶極相互作用可忽略.

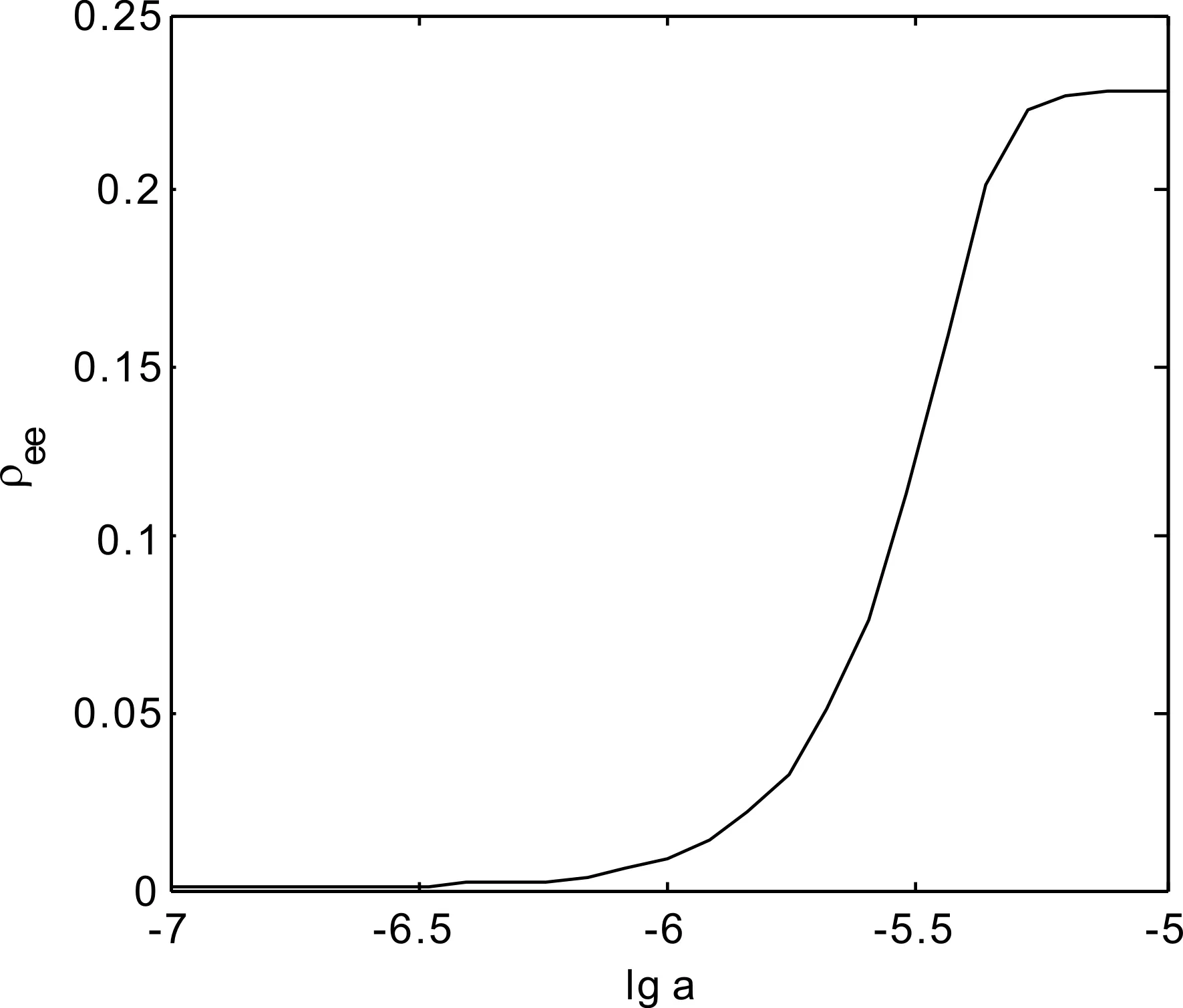
圖4 不同原子間距時的里德堡原子的激發幾率Fig. 4 population of excited Rydberg atoms vs atomic distance

5 結 論

本文利用平均場法計算了給定銣原子團在不同條件下的里德堡態激發幾率，分析了不同主量子數、拉比頻率以及原子密度時里德堡原子的偶極阻塞效應. 原子間的偶極相互作用使里德堡能級頻移，出現偶極阻塞效應，從而降低基態原子激發到里德堡態的幾率. 主量子數越大，原子間的偶極相互作用越強，導致能級頻移越大，偶極阻塞效應越明顯. 激光功率增強，拉比頻率的增大，使得里德堡態的原子數目增加，但這也將導致偶極相互作用的增大，當里德堡原子達到一定數目時，即使再增加拉比頻率，由于偶極阻塞效應里德堡態原子占比達到飽和. 原子密度越大，原子間距越小，原子間的偶極相互作用越強，偶極阻塞效應越明顯. 相反，原子密度越小，原子間距越大，原子間的偶極相互作用越弱.

本文中我們假定所有原子之間的距離是相等的，適用于光晶格中的原子分布，而實驗中捕獲在磁光阱中的原子團是高斯分布，后續我們將在計算中考慮這種非等距分布原子團中的原子的相互作用，并分析其偶極阻塞效應. 偶極阻塞效應的研究有助于量子比特與量子邏輯裝置的實現，促進量子信息與多體物理等領域的發展.