考慮地震力的深水導管與海底土縱向耦合振動研究*

陶磊 趙虹宇 鄧嵩 朱碩 耿浩然 王相 紀夢楠

常州大學

深水淺部地層的膠結(jié)質(zhì)量差，固井難度大，海底地震來臨時，對表層套管柱和海底管線可能會造成較大的破壞。據(jù)統(tǒng)計美國威名頓、中國大慶以及俄羅斯薩格勒布的油藏有超過1 000口由于地震引起的套管損毀井[1]。在鉆井過程中，水下井口-導管面臨著隔水管張力、淺層土耦合作用以及地震載荷的影響[2]。

深水水下井口-導管與海底土耦合振動的研究大多以樁基力學為基礎，最典型的樁土模型是Winker和Novak模型[3]，但這兩個模型都忽略了土層中縱向應力的變化。胡昌斌等建立了一個三維軸對稱模型[4]；朱幸科等研究了深水采油套管柱的縱向振動[5]，但沒有考慮地震力的影響；ELSAYED等進行了地震力下導管架平臺的分析，其沒有涉及到水下井口-導管的分析[6]；有部分學者做了地震活動下海底管線的動態(tài)規(guī)律研究，但沒考慮縱向上與海底土的耦合作用[7]。綜上，水下井口-導管振動分析還處在初步階段，大多數(shù)沒有考慮到耦合作用以及地震力的影響。本文建立了一個考慮地震力的水下井口-導管與海底土的縱向振動耦合模型，在模型中同時考慮了井口上段隔水管的張力、鉆井液上返引起的縱向摩擦力以及地震力，將海底淺層土假設為固液兩相的飽和黏性土，運用Flourier變換得到了水下井口頻域內(nèi)的振動特征，并將計算結(jié)果與ABAQUS模擬結(jié)果以及單相土的計算結(jié)果對比，準確度較高。

1 模型建立

1.1 模型假設

模型假設如下：①海底土是均勻、各向同性、具有黏彈性的飽和土；②海底土壤介質(zhì)由土壤骨架和孔隙流體組成；③隔水管導管材料是彈性材料，上返鉆井液是黏彈性流體；④導管和土形成的系統(tǒng)間的縱向位移很小，系統(tǒng)接觸面變形和力是連續(xù)的；⑤地震力為海底土底部瞬時的簡諧激振力；⑥導管的BOP頂部有一個由隔水管縱向張力引起的向上的固定力。

耦合作用簡化模型如圖1所示。

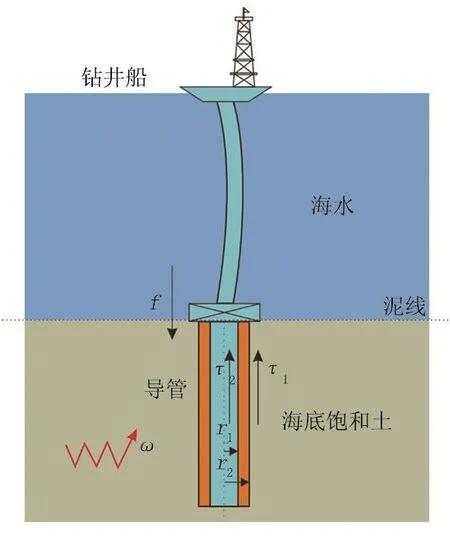
圖1 水下井口-導管與海底土耦合作用模型Fig.1 Coupling model of underwater wellhead-pipe and seafloor soil

1.2 控制方程

（1） 海底土層縱向振動方程。海底土層為固液兩相飽和黏性土，依據(jù)土動力學原理，建立軸對稱柱坐標系的動態(tài)平衡方程如下

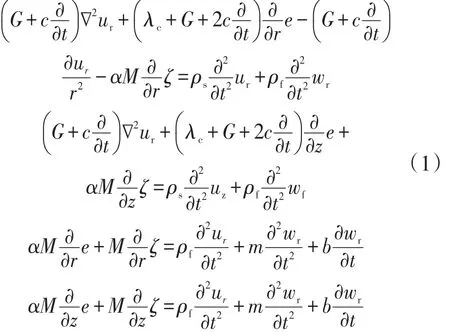
其中

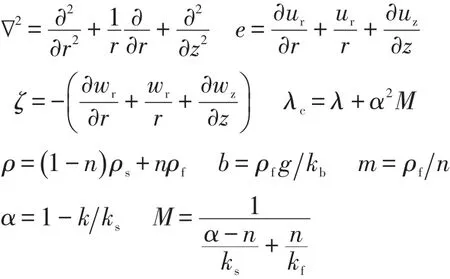
式中：ur、uz分別為土壤骨架的徑向和垂直位移，mm；wr、wz分別為孔隙流體的徑向和垂直位移，mm； ρs、ρf分別為土壤骨架和孔隙流體的密度，g/cm3； ks、kf、kb分別為土壤骨架、孔隙流體和套管柱的體積彈性模量，MPa；λ、G為土壤的拉梅常數(shù)；c為土壤的黏性阻尼；ρ為飽和土壤的質(zhì)量密度，g/cm3；n為土壤的孔隙度。

當發(fā)生地震時[8]

式中：β為土壤的阻尼率；ω為地震的角頻率。

（2）水下井口-導管的縱向振動方程。水下井口-導管系統(tǒng)在縱向上受到隔水管張緊力、土壤耦合摩擦力以及導管內(nèi)鉆井液上返流動摩擦力的作用，振動方程為

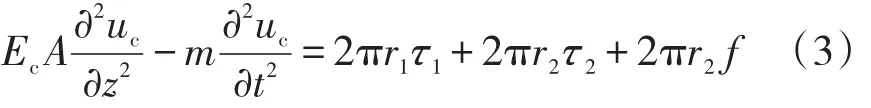
式中：Ec為套管柱截面的楊氏模量，GPa；uc為井口-導管系統(tǒng)的縱向位移，m；τ1為土壤對導管的垂向阻力，N；τ2為導管內(nèi)上返流體的向上摩擦力，N； f為隔水管的張緊力，假設為恒定力，N；r1、r2分別為導管的內(nèi)徑和外徑，mm。

1.3 邊界條件

（1）海底土邊界條件。海底土層頂部的位移為0，即

海底土層底部位移為地震力的振幅，即

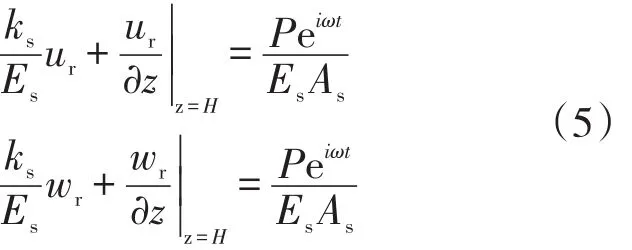
海底土層位移在水平方向上無窮大

海底土層的初始狀態(tài)為

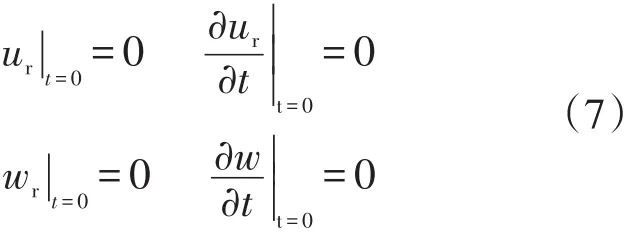
（2）水下井口-導管邊界條件。系統(tǒng)頂部和底部的位移為

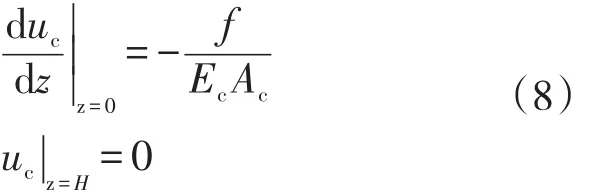
水下井口-導管的初始狀態(tài)為

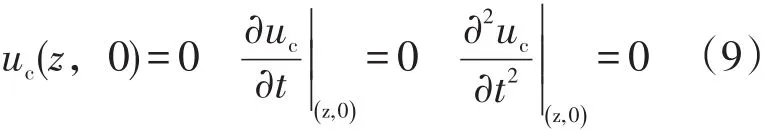
（3）水下井口-導管與海底土耦合條件。海底土壤與導管之間位移連續(xù)，方程為

海底土壤與導管之間作用力相反，方程為

2 模型求解

當海底發(fā)生地震時，可以將海底地震簡化為縱向上瞬時的簡諧力，振幅為eiωt，此時海土層的振幅也為 eiωt。

2.1 土層振動問題求解

首先引入勢函數(shù)，令

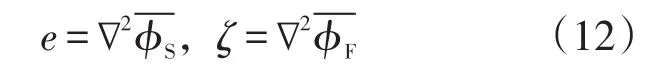
對式（1）進行Laplace變換得

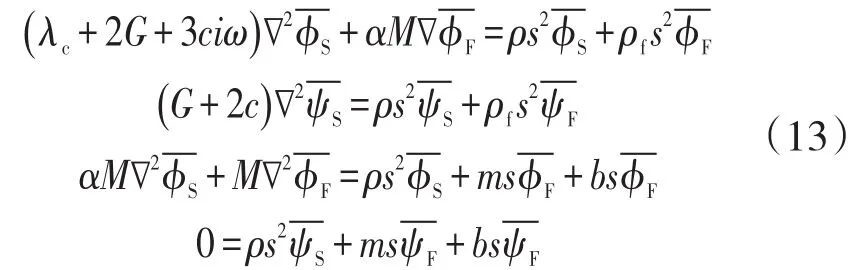
可以得到方程的一般解為

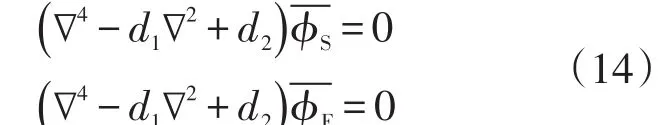
其中

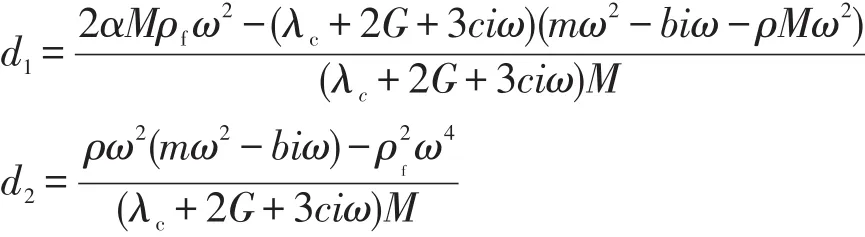
代入海底土層的邊界條件，當r趨向于無窮大時，應力和應變?yōu)?，可以得到下式

C1、C2、C3、C4、C5、C6是待定系數(shù)，它們之間的關(guān)系可以表示為

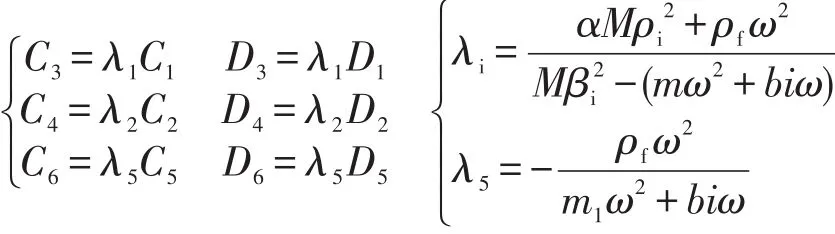
待定系數(shù)可以通過邊界條件求得，代入海底土層的位移條件、導管與海底土界面條件可求得

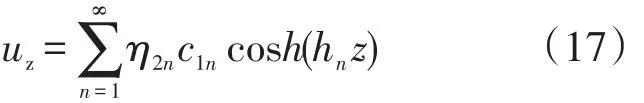
其中

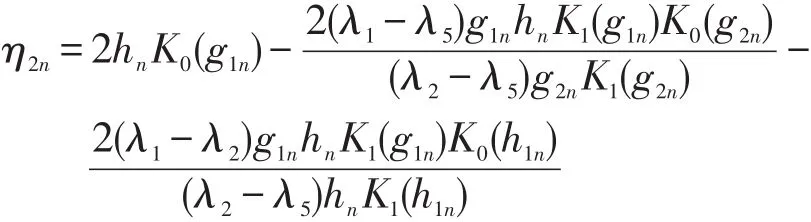
2.2 井口-導管振動問題求解

從前述可得到

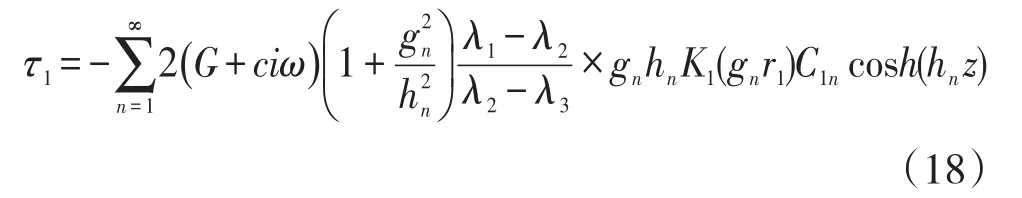
用Herschel和Bulkley模型描述鉆井液剪切力[9]，因此τ2可表示為

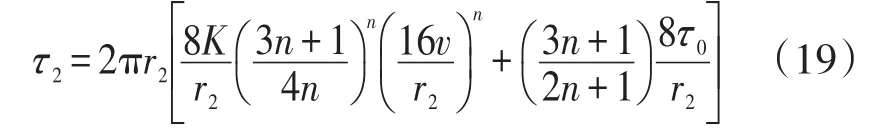
將方程（18）和（19）帶入方程（7），根據(jù)Laplace變換，可得

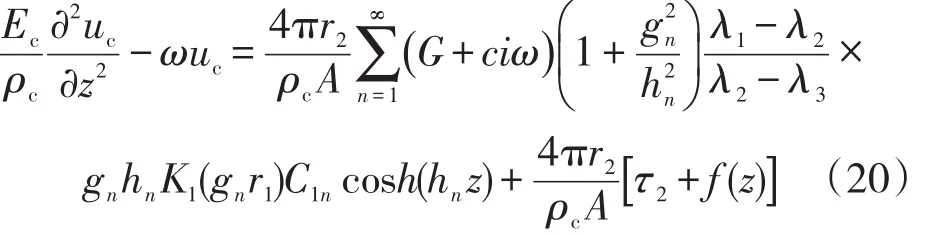
方程（20）的解可表示為

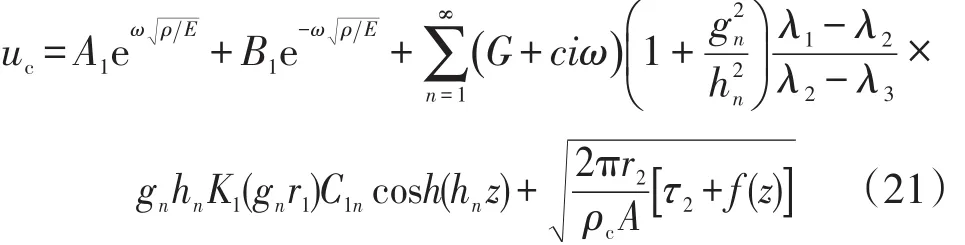
其中，cosh(hnz)在區(qū)間[0 ， θ]內(nèi)表示為

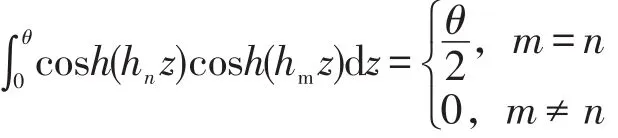
可求得C1n，因此方程（21）的解為

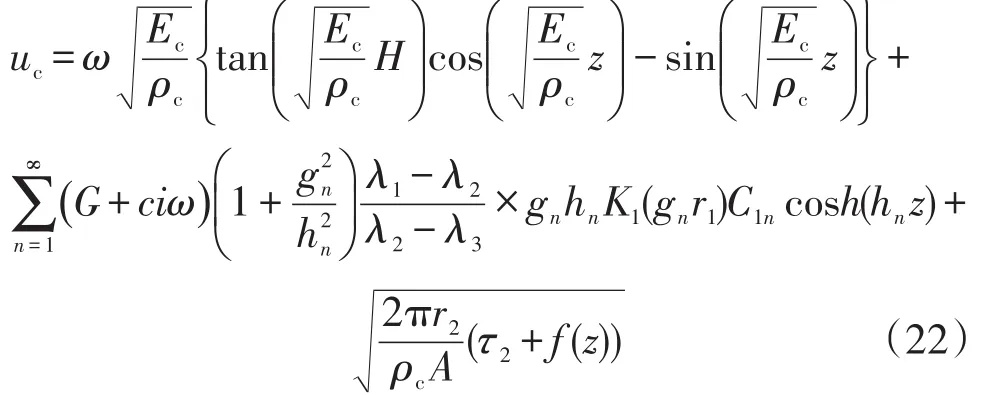
3 算例分析

3.1 計算數(shù)據(jù)

用南海某井數(shù)據(jù)以及海底土壤性質(zhì)對深水導管與海底土縱向耦合振動進行計算分析。通常導管的入泥深度不能過大也不能太小，不然會導致承載力不足或耗時過多，一般為30～100 m，取導管下入深度為60 m，其余具體計算數(shù)據(jù)如表1所示[10]。

3.2 計算結(jié)果

將海底土假設為單相，與本文的計算結(jié)果對比可知，井口剛度和阻抗振幅與單相土計算結(jié)果基本吻合，剛度隨著頻率的增加而減小，阻抗隨著振動頻率增加而增加；當振動頻率較低時，兩相海底土的振動阻抗小于單相土（圖2）。同時運用Abaqus軟件，將本文計算結(jié)果與Abaqus模擬結(jié)果進行對比（圖3），兩者基本吻合。

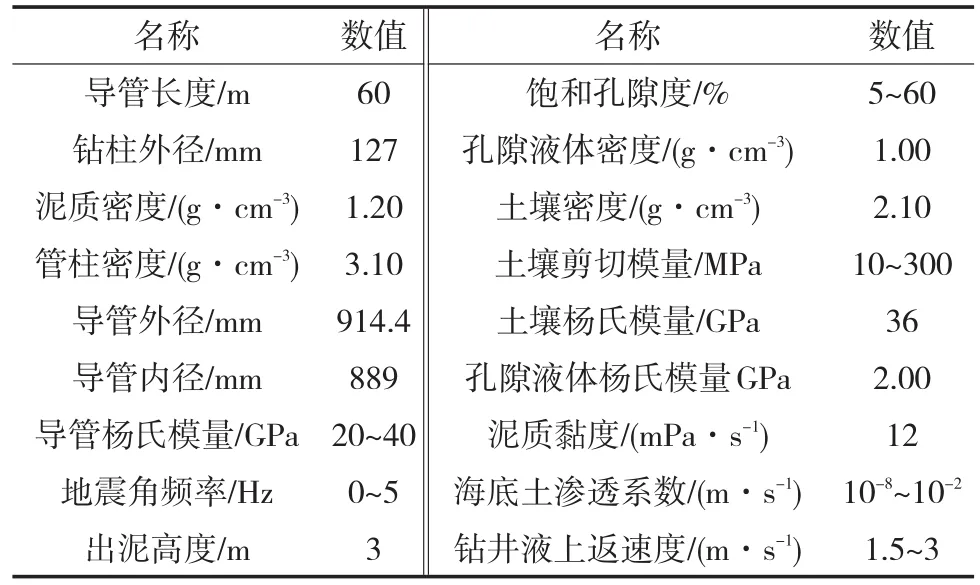
表1 深水井及海底淺層土性質(zhì)數(shù)據(jù)Tab.1 Performance data of deepwater wells and seafloor shallow soil

3.3 影響因素分析

研究了剪切模量、孔隙度、導管長度、鉆井液上返速度以及鉆井船縱向的振幅等參數(shù)對水下井口-導管振動阻抗的影響，結(jié)果如圖4～圖8所示。

圖4所示為土壤剪切模量分別為20和10 MPa時井口-導管的剛度和阻抗振蕩幅度，從圖中可以看出，隨著剪切模量的增大，剛度和阻尼振蕩幅度都減小。圖5所示為土壤孔隙度對剛度和阻抗的影響，當孔隙度較大時，剛度和阻尼振蕩幅度增大；剪切模量和孔隙度對井口-導管縱向振動的影響較小。圖6所示為導管長度對井口-導管振動的影響，剛度和阻尼的變化幅度隨著導管長度增加而減小，而且較為明顯。圖7所示為鉆井液上返速度對井口-導管的影響，變化幅度隨著鉆井液上返速度增加而增大，影響較小。從圖8可以看出，鉆井平臺或鉆井船縱向波動幅度對井口-導管剛度和阻尼影響較大，且隨著縱向振幅的增加而增大。

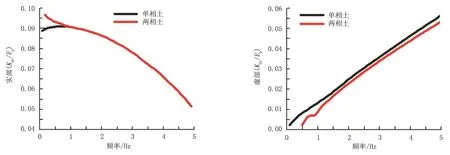
圖2 兩相土與單相土對比Fig.2 Comparison of two phase soil and single phase soil

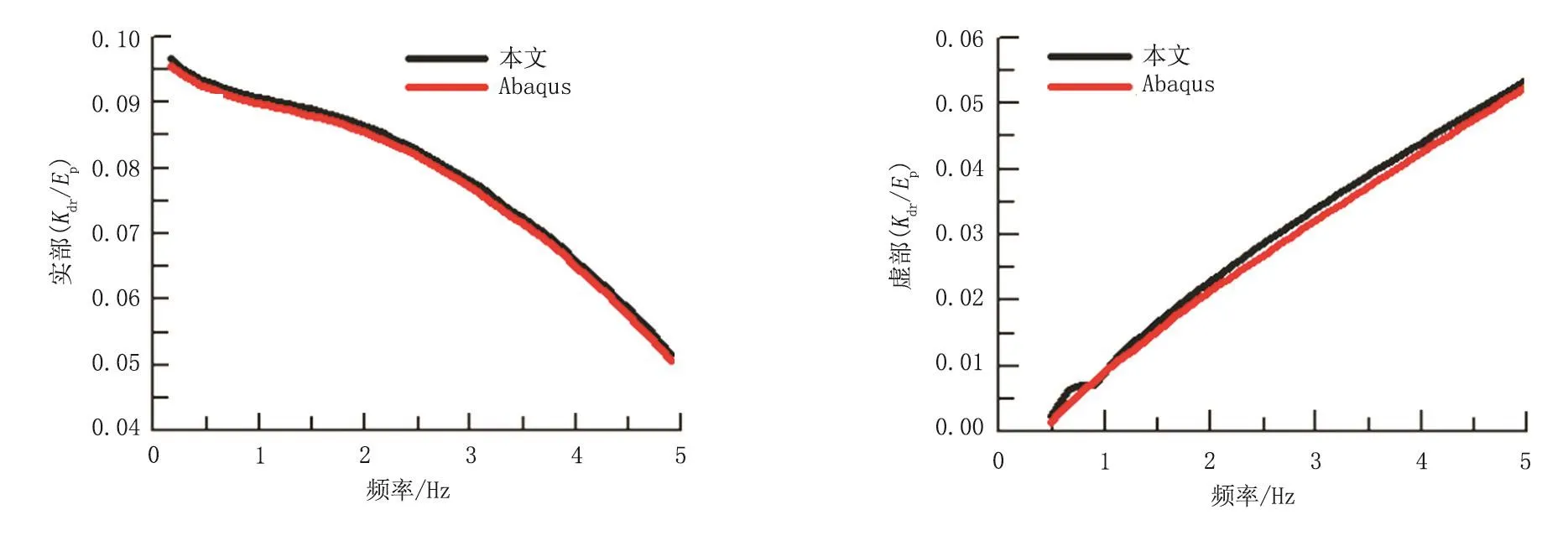
圖3 本文結(jié)果與Abaqus模擬結(jié)果對比Fig.3 Comparison of the results of this paper and the solutions of Abaqus

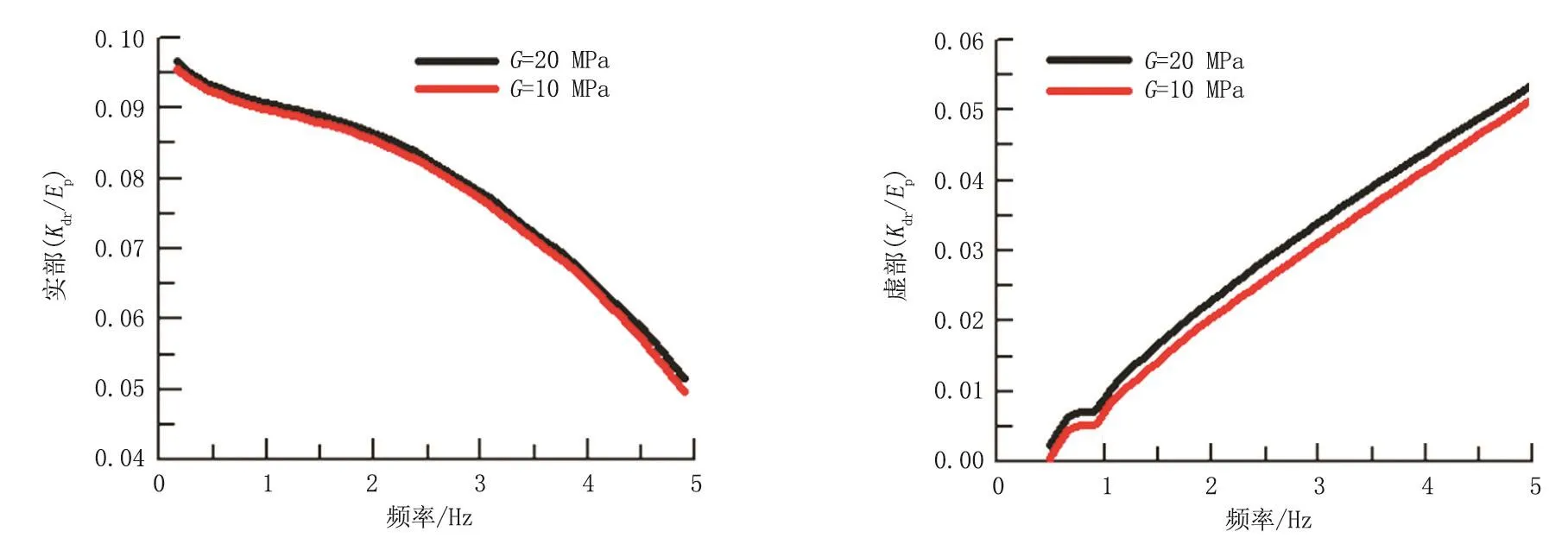
圖4 土壤剪切模量對振動阻抗的影響Fig.4 Effect of the shear modulus of soil on vibration impedance

圖5 土壤孔隙度對振動阻抗的影響Fig.5 Effect of the porosity of soil on vibaration impedance

圖6 導管長度對振動阻抗的影響Fig.6 Effect of the length of conductor on vibration impedance

圖7 鉆井液上返速度對振動阻抗的影響Fig.7 Effect of the mud rising rate on vibration impedance

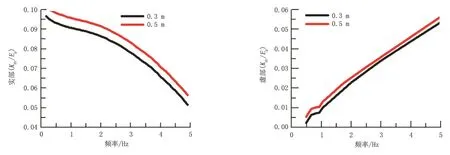
圖8 鉆井平臺或鉆井船振幅對振動阻抗的影響Fig.8 Effect of the amplitude of drilling plate or vessel on vibration impedance

4 結(jié)論

（1）導管下入深度越深，井口-導管的軸向力產(chǎn)生的縱向振動降低的幅度越大。

（2）地震頻率越大，水下井口-導管的縱向振動幅度增加越大。

（3）鉆井液上返速度對井口-導管的縱向振動影響較小。

（4）鉆井船或者平臺的縱向振動對井口-導管的縱向振動有影響。

（5）海底土的剪切模量和孔隙度都將影響水下井口-導管的縱向動態(tài)性能。

（6）由于深水海底土膠結(jié)差，存在低溫高壓等特殊現(xiàn)象，造成對鉆井設備特性的要求有所不同；同時地震力也影響鉆井管柱的動態(tài)性能。

本文的研究對于深水、超深井鉆完井作業(yè)具有重要的意義，但也存在著一些不足，如海流力、隔水管軸向力的變化，溫度、壓力的變化等對管柱動態(tài)性能的影響都需要進一步研究。