側(cè)面俯視時盛滿水的碗中斜插筷子的虛像位置研究

(南京曉莊學(xué)院電子工程學(xué)院,江蘇 南京 211171)

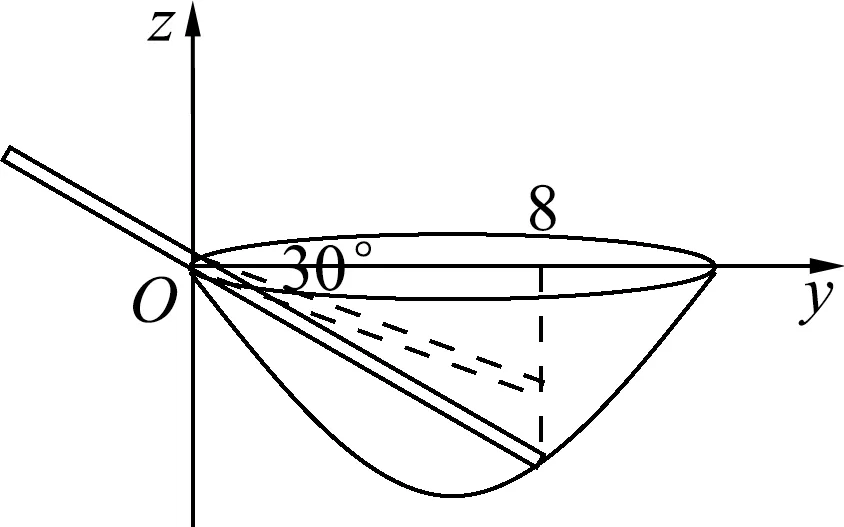
圖1 側(cè)面俯視時盛滿水的碗中筷子的虛像

眾所周知,從側(cè)面俯視盛滿水的碗中的斜插筷子時,會看到水中的筷子自水面處向上偏折,且視角(目光與水面法線即豎直方向的夾角)越大偏折越厲害,見圖1.設(shè)筷子本身與水平方向的夾角為30°,碗里的筷子部分在水平方向的投影長度為8cm.但卻少有人知道筷子虛像的準(zhǔn)確位置以及虛像仍然呈現(xiàn)直線段形狀的根本原因,更少有人知道筷子的虛像實(shí)際上還會向觀察者這邊偏折.本文將利用已有的光學(xué)知識計(jì)算出水中筷子虛像的準(zhǔn)確位置,并運(yùn)用MATLAB軟件作出虛像的三維圖像并加以分析.

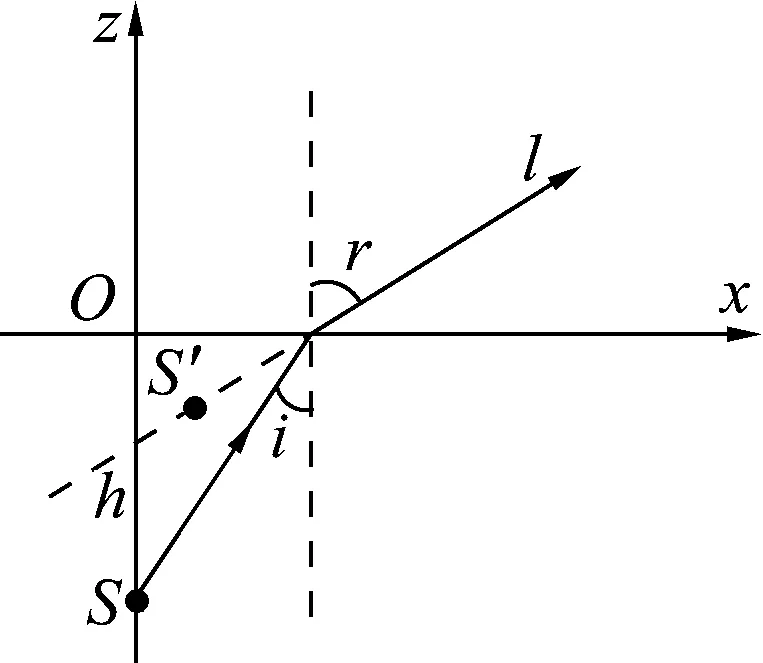
圖2 來自水中物點(diǎn)的光線的折射

圖2顯示的是來自水下h深度的物點(diǎn)S的某條光線l,其入射角為i,折射角即人眼視角為r,像點(diǎn)S′就在折射光線的反向延長線上,且在物點(diǎn)S的右上方.[1]姚啟鈞《光學(xué)教程》(第4版)[2]給出像點(diǎn)S′的坐標(biāo)如下

x=h(n2-1)tan3i，

(1)

(2)

其中水的折射率n=4/3.由于這里的物點(diǎn)S來自圖1中水面以下的筷子,因此可將物點(diǎn)的深度h表示成

(3)

將式(3)分別代入式(1)、(2)并考慮到n=4/3后,即得像點(diǎn)S′的空間軌跡方程

(4)

(5)

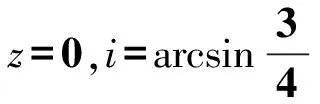
設(shè)視角r=30°和60°,則由折射定律sini=sinr/n可算出i=22.0°和40.5°,繼而得到tani=0.405和0.854.將tani值代入式(4)、(5)便得在這兩個視角下筷子虛像的位置

當(dāng)r=30°時，

x=0.030y,z=-0.353y，

當(dāng)r=60°時，

x=0.280y,z=-0.123y，

其中y∈[0,8] cm.

運(yùn)用MATLAB軟件可作出水中筷子實(shí)物及其虛像的三維圖像,見圖3和圖4.當(dāng)然,我們實(shí)際看到的只有虛像.從圖中可見,或更精確地從上面式子算得,在30°和60°視角下筷子的虛像與右邊“網(wǎng)格墻”的交點(diǎn)坐標(biāo)分別為(0.24,8,-2.82)和(2.24,8,-0.98),而筷子實(shí)物與右邊“網(wǎng)格墻”的交點(diǎn)坐標(biāo)則是(0,8,-4.62).顯然60°視角下筷子的

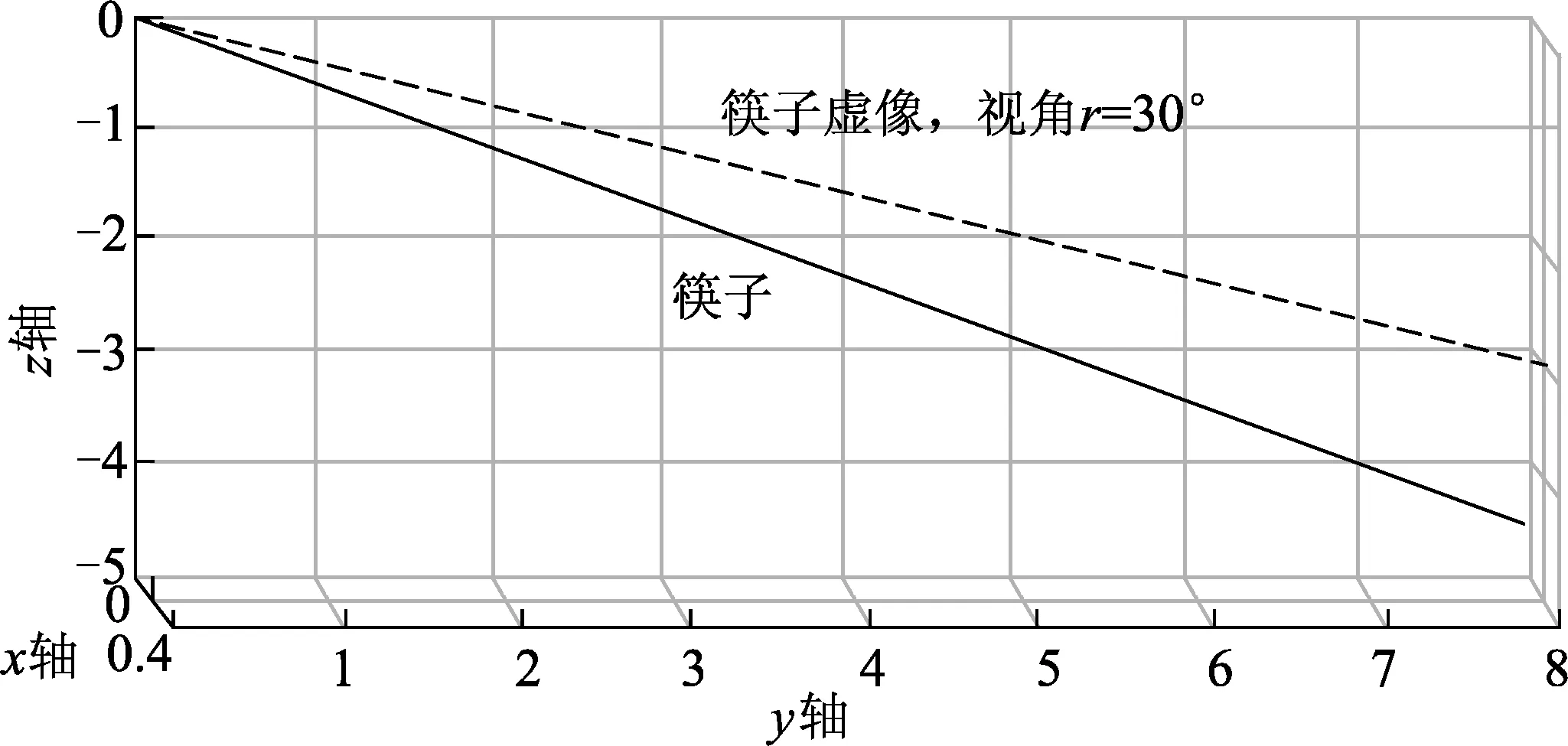
圖3 碗內(nèi)水中的筷子實(shí)物與其在30°視角下的虛像

圖4 碗內(nèi)水中的筷子實(shí)物與其在60°視角下的虛像

虛像相對于實(shí)物要向上(z軸正方向)、向外(x軸正方向)偏折許多.不過,由于我們看到的碗底也是虛像,它和筷子端的虛像同步移動,以及我們從側(cè)面觀察的視覺緣故,我們雖然能明顯地看到筷子向上偏折,卻不易看到筷子向我們眼睛這邊偏折.除非你把筷子換成標(biāo)有刻度及文字的尺子,并用近視的裸眼去仔細(xì)觀察.

需要說明的是,虛像的位置是隨視角變化的,30°視角和60°視角下筷子虛像的位置是不同的,因此這兩個虛像宜分圖畫出,如圖3和圖4,代表著兩個不同的視角.事實(shí)上,筆者在作圖3、4時已考慮了此視角因素.另外,嚴(yán)格地講,本文計(jì)算的實(shí)際是筷子的子午虛像．[2,3]若將圖3、4中筷子的子午虛像(虛線)沿著目光的方向向O-yz平面投影,即得筷子的另一理論虛像——弧矢虛像．顯然這兩個虛像總是重疊在一起的,我們的目光只能聚焦于前面的子午虛像,永遠(yuǎn)無法透視看到后面筷子的弧矢像,因此這里用筷子的子午虛像作為筷子虛像是準(zhǔn)確的.