考慮蒸發鋒面的包氣帶一維液相運動方程解析解

劉夢茹, 程大偉, 盧玉東

(1.長安大學 環境科學與工程學院, 陜西 西安 710054; 2.長安大學 旱區地下水文與生態效應教育部重點實驗室, 陜西 西安 710054)

1 研究背景

包氣帶是大氣水、地表水、地下水三者之間發生水力聯系并進行水分交換的場所，同時也是地表污染物進入地下的通道。因此包氣帶中液相運動的研究在地下水污染管理、維持地下水采補平衡[1]等領域中有著廣泛的應用。包氣帶中土壤濕度是控制水分交換的關鍵因素，其狀態受季節和氣候變化的影響[2]。在雨季，降雨作用在包氣帶中形成的液相運動為穩態入滲[3]；在旱季，土面蒸發和植物蒸騰是控制包氣帶中潛水位以上區域液相運動的主要因素。多數學者在推導包氣帶液相運動方程時僅考慮入滲情況，而由蒸發所引起的包氣帶液相運動在實際中大致可以分為以下兩種形式[4-7]：當地下水位深度足夠淺時，包氣帶液相運動完全受毛細作用控制，始終維持水力連續，且服從達西定律;當地下水位深度超過某一臨界深度時，受到重力因素及黏滯力的影響，蒸發鋒面[7]將會由地表向地下水位發展。

在推導包氣帶一維液相運動方程解析解過程中常用冪函數型或指數型滲透函數，諸如線性模型[8]、基于Brooks-Corey土水特征曲線建立的滲透性函數模型[9]、低飽和度下Van Genuchten 模型[10-11]、常數滲透系數模型[12]等均為冪函數型滲透性函數[3]。由于冪函數型滲透性函數在推導液相運動方程解析解時變量難以合并,導致所獲得的解析解常為負壓水頭的隱式表達，此外，在求解的過程中這些解僅考慮入滲情況。Gardner模型為指數型滲透系數函數，可對液相運動方程進行線性化處理，易推導解析解。在穩態入滲或蒸發條件下,一維液相運動方程的解析解相比數值解簡潔[13],并且易基于相應解析解建立反演模型,進行參數反演，從而具有廣泛的實際應用,如通過實測數據反演估計水力參數、為更復雜的液相運動提供標準測試方案等。

本文基于指數型滲透系數模型Gardner模型求解擴散度，分別推導在穩態入滲和穩態蒸發兩種情況下包氣帶中均質土和成層土液相運動方程的解析表達以及蒸發鋒面深度表達式。分析各水力參數對一維液相運動方程的影響并通過解析解進行水力參數的反演。

2 均質土水力連續區有效飽和度剖面及蒸發鋒面深度的解答

LU Ning等[14]通過給定適當的初始條件和邊界條件，推導出以基質吸力為變量的液相運動方程解析解。本節在此基礎上，推導出有效飽和度剖面解析解。

2.1 均質土水力連續區液相運動方程解析解

一維穩態流下包氣帶液相運動方程邊值問題可寫作如下形式：

(1)

式中：θ為含水量，m3/m3；D(θ)為擴散率；K(θ)為非飽和土滲透系數，m/s。

非飽和土的滲透系數是負壓水頭的函數，常被定義為：

K=KsKr

(2)

式中：Ks為飽和土滲透系數；Kr為相對滲透系數。

在非飽和土中,相對滲透系數Kr和含水量θ均為負壓水頭的函數[15]。Gardner模型常被用于求解析解，所描述的相對滲透系數與負壓水頭之間呈指數關系，即

Kr=eαgh

(3)

式中：αg為Gardner模型參數。

(4)

式中:Se為有效飽和度;θr為殘余含水量;θs為飽和含水量。公式(4)即為Srivastava提出的指數型土水特征關系[16]。

將公式(4)轉化為負壓水頭與有效飽和度的關系，則有：

(5)

將式(5)代入式(1)，則為負壓型液相運動方程。文獻[14]給定下邊界為水頭邊界條件，即z=0時，負壓水頭為h0；上邊界為流量邊界條件，即z=H，比流量為q，建議了如公式(6)的解析解：

(6)

當采用負壓水頭h為變量時,公式(6)中μa-μw的絕對值與負壓水頭絕對值大小相等，將公式(4)及公式(6)化簡合并得：

(7)

公式(7)即為包氣帶一維液相運動方程解析解，該解析解表明土層中有效飽和度剖面受比流量、下邊界負壓水頭、孔隙分布特征和滲透性控制。

若下邊界為潛水位時，則z=0,h0=0,有：

(8)

2.2 均質土蒸發鋒面深度

若規定比流量q在入滲時為負，蒸發時為正，當比流量q小于臨界比流量qc時，液態水飽和度剖面在整個區域內延伸。當比流量q大于臨界比流量qc時，自地表以下至蒸發鋒面處土孔隙內流體為氣體，液態水僅存在于潛水面至蒸發鋒面區間內。定義蒸發鋒面處的有效飽和度為臨界有效飽和度Sec。參考Hayek[3]建議采用在地表處土中水有效飽和度為零時對應的蒸發率為臨界比流量，即:

z=H,Se=0

(9)

將公式(9)代入公式(8)，則有：

(10)

當q>qc時，只需要將臨界有效飽和度Sec代入公式(7)即可推導得蒸發鋒面深度(蒸發鋒面距離地下水位的高度)為：

(11)

公式(11)表明蒸發鋒面深度除受比流量、孔隙分布特征和滲透性影響外，還與臨界有效飽和度Sec有關。

3 成層土水力連續區有效飽和度剖面及蒸發鋒面深度的解答

均質土的分析常用于實驗室研究,成層土常見于實際工程中。根據Darcy定律和質量守恒定律推導包氣帶中成層土液相運動方程的解析解以及相對應的蒸發鋒面深度模型。

3.1 成層土水力連續區液相運動方程解析解

現討論兩種滲透性不同的土構成非飽和成層土[17]的情形，如圖1所示。令土層的總厚度為L,土層1的厚度為z1,土層2的厚度為L-z1。土層1和土層2的界面位置在z=z1處，每層土為均勻線彈性均質土。根據Darcy定律和質量守恒定律，非均質界面處土層1和土層2應滿足負壓水頭和比流量分別相等。即有：

h1z1=h2z1

(12)

q1z1=q2z1

(13)

式中:h1z1、h2z1分別為非均質界面土層1的負壓水頭和土層2的負壓水頭；q1z1、q2z1分別為非均質界面處土層1的流量和土層2的流量。

圖1 成層土剖面示意圖

土層1底面為地下水位，故利用式(7),可得土層1中有效飽和度剖面為：

參考譯文:Konka Group has been granted“National Advanced Quality and Benefit Enterprise”and“National Customer Satisfied Enterprise”for several years．

(14)

當z=z1時，根據負壓水頭和有效飽和度的關系，可知：

=h2z1

(15)

故對于土層2，其有效飽和度剖面為：

(16)

3.2 成層土蒸發鋒面深度

對于成層土而言，在穩態蒸發條件下，蒸發鋒面深度受比流量影響較大，參考Hayek[3]的建議，本文為便于處理,取土層2頂部有效飽和度為零所對應的比流量為土層2的臨界比流量qc2，即z=L,se2=0，代入公式(16)可得土層2的臨界比流量應滿足：

qc2=

(17)

定義蒸發鋒面位于土層非均質界面處所對應的比流量為臨界比流量qcl。當蒸發鋒面深度zDF=z1時，即土層2在非均質界面處的有效飽和度Se2,z1為土層2的臨界有效飽和度Sec2。將該條件代入公式(16)，可得非均質界面處的臨界流量qcl為：

(18)

定義成層土中各土層按所計算土層頂部有效飽和度為臨界飽和度計算臨界比流量，則土層1的臨界比流量應滿足當z=z1時Se1=Sec1，代入公式(14)可得：

(19)

當qc2≤q≤qc1時，蒸發鋒面在土層2內，則由公式(16)可得蒸發鋒面深度為：

(20)

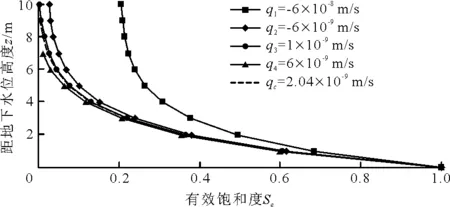
當q≥qc1時，蒸發鋒面可能在土層1內時，若比流量q

(21)

此時，在土層1中0≤z≤zDF內有液態水運動，并服從達西定律。

4 水力參數反演

解析解重要的一種應用是反演水力參數。水力參數反演的難易程度取決于反演參數的個數。解析式(8)中涉及的水力參數包括Gardner模型參數αg和飽和滲透系數Ks。通過假設已知土層底面為潛水面來反演上述2個參數，比流量q、負壓水頭h1、z1處的有效飽和度Se1、z2處的有效飽和度Se2均為已測定值，具體反演過程如下：

將(z1,Se1),(z1,h1)代入公式(4)及公式(8)，化簡可得：

(22)

將(z2,Se2)代入公式(8)求得αg的表達式如下：

(23)

將公式(22)代入公式(23)，整理可得：

(24)

公式(24)是關于αg的超越方程，需利用迭代求根法求解。

5 結果與討論

5.1 比流量q和模型參數αg對有效飽和度剖面的影響

圖2所示為厚度H=10 m土層在不同比流量q下有效飽和度剖面。主要參數依次為：αg=0.5 m-1,Ks=3×10-7m/s,qc=2.04×10-9m/s，q1=-6×10-8m/s，q2=-6×10-9m/s，q3=1×10-9m/s，q4=6×10-9m/s。根據圖2可知，當比流量小于臨界比流量時，地表處的有效飽和度隨著比流量的增大而減小，且不同比流量下有效飽和度剖面之間的差異隨距離地下水位高度的減小而減弱。當比流量大于臨界比流量時，土層中存在蒸發鋒面。土中飽和度剖面以下所圍面積反映了土層中液態水質量分數相對大小，隨著比流量的增大，土層中液態水質量分數減小。

圖2 不同比流量下有效飽和度-深度關系曲線

圖3為厚度H=10 m土層在不同模型參數αg下有效飽和度剖面。地下水位于土層地面以下10 m處。主要參數為：αg取值分別為0.05、0.5、1、2 m-1,q=-3×10-8m/s，Ks=3×10-5m/s,由圖3可知αg對有效飽和度剖面影響較大，相同深度處的有效飽和度隨αg值得增大而減小。當αg值較大(如αg=2 m-1)時，地表下部土層一定區域內的有效飽和度近似等于地表處的有效飽和度，在該區域以下有效飽和度會驟增，直至地下水位處變為1。此時液相運動主要受重力控制。當αg值較小(如αg=0.05 m-1)時，毛細作用發揮支配作用，有效飽和度趨于線性變化。

圖3 不同αg下有效飽和度-深度關系曲線

5.2 成層土中有效飽和度剖面的變化特征

為分析穩態流下成層土有效飽和度隨深度的變化，設定土層A和土層B的厚度均為5 m。土層A的主要參數為：αg=1 m-1，Ks=3×10-5m/s;土層B的參數為:αg=0.5 m-1，Ks=3×10-7m/s。土層A具有比土層B較高的孔隙連通狀態和透水性。

5.2.1 入滲條件下成層土有效飽和度剖面 圖4為穩態入滲條件下成層土內有效飽和度剖面。其中工況1為土層B在上部，土層A在下部；工況2為土層A在上部，土層B在下部。比流量q=-3×10-8m/s。

工況1情況下，上部土層B的有效飽和度小于相同深度處均質土B的有效飽和度；工況2情況下，上部土層A的有效飽和度大于相同深度處均質土A的有效飽和度。而對于下部土層，由于下邊界水頭與均質土下邊界條件相同，無論是工況1還是工況2均與對應均質土層的有效飽和度-深度關系曲線重合。

圖4表明穩態入滲下，當下部土層透水性較好時，上部土層中的液態水向下層流動，液相運動增強，其有效飽和度與均質土相比要小。反之，當下部土層透水性較差時，上部土層中的液態水向下層流動受到阻滯，液相運動減弱，其有效飽和度與均質土相比要大。

圖4 入滲條件下成層土有效飽和度-深度關系曲線

5.2.2 蒸發條件下成層土有效飽和度剖面 圖5為穩態蒸發條件下成層土的有效飽和度剖面。其中，工況3為土層B在上部，土層A在下部；工況4為土層A在上部，土層B在下部。比流量q=1×10-8m/s。由圖5可知，在蒸發條件下工況3的上部土層B內有效飽和度大于相同深度處均質土B的有效飽和度；工況4的上部土層A的有效飽和度小于相同深度處均值土A的有效飽和度。下部土層中，由于下邊界水頭與均質土下邊界條件相同，工況3、工況4均與對應的均質土層的有效飽和度-深度關系曲線重合。

對比上部土層的有效飽和度，可以發現在穩態蒸發下，若下部土層透水性較好，上部土層中液相運動增強會儲存較多的液態水，同時蒸發鋒面距地表更淺；反之，當下部土層透水性較差時，上部土層中液相運動受阻減弱，儲存液態水較少，蒸發鋒面距地表更深。

圖5 蒸發條件下成層土有效飽和度-深度關系曲線

5.3 參數反演分析

5.3.1 參數反演模型的可靠性 假設土層底面為地下水位，給定q=-3×10-8m/s,αg=0.5 m-1，Ks=3×10-7m/s。選擇兩個觀測點Z1=8 m,Z2=4 m,利用公式(8)獲得Z1處有效飽和度精確解為0.116 5，將Z1處精確解代入公式(5)中，可得負壓水頭的精確解為-4.299 73；Z2處的有效飽和度精確解為0.221 8。將上述數據代入公式(24)中求得αg值為0.5 m-1,再代入公式(22)求得Ks值為3×10-7m/s。結果表明參數反演模型的正確。

6 結 論

本文利用相對滲透系數模型中的Gardner模型分別推導了均質非飽和土和成層非飽和土中一維液相運動方程解析解，獲得了蒸發鋒面深度的計算表達式，所得結論具體如下：

(1)包氣帶中均質土有效飽和度是深度的函數，受比流量、下邊界負壓水頭、Gardner模型參數等參數控制。相同深度處的有效飽和度隨著比流量和Gardner模型參數的增大而減小。

(2)對于給定比流量和土層參數的非飽和成層土中，土層內的有效飽和度剖面主要受下邊界負壓水頭控制。在穩態入滲或穩態蒸發條件下，下部土層的有效飽和度剖面與相應均質土的有效飽和度剖面重合；上部土層的有效飽和度受下部土層透水性的影響。

(3)由于蒸發鋒面的存在，包氣帶中均質土和成層土液相運動方程的解析解的適用范圍在臨界有效飽和度與飽和有效飽和度之間。

(4)測試了參數反演模型的可靠性，分析測量數據誤差對參數反演結果影響。結果表明所建議的參數反演表達式是可靠的，參數反演的結果受測量誤差的影響較小。