《一次函數的圖象與性質》課例設計
陳 姍
(廣東省珠海市第十中學 519000)
一、背景介紹
本課是教研公開課,課例進行了積極設計,意在學生在教師指導下能順利落實學習目標,理解并掌握課本的知識點,培養學生的動手操作能力、合作探究能力.
二、備課過程
1.地位作用
一次函數是各類函數中最簡單的一種,反映了函數特點及函數的思維方式、研究方法和應用模式,因此學好一次函數是學好其他函數的基礎.
2.課標要求
學生能畫出一次函數圖象,根據圖象和表達式y=kx+b(k≠0)探索并理解k>0和k<0時圖象的變化情況.
3.教材理解
補充:當直線y1=k1x+b1與y2=k2x+b2平行時,則k1=k2且b1≠b2,反之亦成立;常數項b對圖象的影響.
4.中考分析
利用函數圖象求系數取值范圍,或根據系數判斷函數圖象位置;運用一次函數知識解決實際問題如利潤最大;利用方程(組)確定函數圖象特殊點(公共點)坐標,利用一次函數圖象求一元一次不等式(組)解集等;一次函數與其他代數、幾何知識綜合應用.
5.學情分析
八下學生思維活躍趨成熟,但好奇心不減,具備抽象、猜想、歸納、證明、總結等能力,且學生已有研究函數圖象與性質的經驗和方法.
三、教學設計
學習目標:(1)會用兩點法畫一次函數的圖象;(2)能從圖象角度理解正比例函數與一次函數的關系;(3)能根據一次函數的圖象和表達式y=kx+b(k≠0),理解k、b對函數圖象的影響.
重、難點:k、b的值與圖象位置的關系.
(一)復習與預習
復習:1.畫函數圖象的步驟;2.正比例函數與一次函數的關系;3.正比例函數y=kx(k≠0)的圖象和性質.預習:展示學生所畫函數y=x、y=x+2、y=x-2的圖象.
(二)探究新知
活動一:探究一次函數與正比例函數的聯系觀察函數y=x、y=x+2、y=x-2的圖象.
總結:
1.形狀:一次函數y=kx+b的圖象是一條____線
2.平移規律:一次函數y=kx+b的圖象可以由直線y=kx平移____個單位長度得到:當b>0時,它是由y=kx向____平移____個單位長度得到;當b<0時,它是由y=kx向____平移____個單位長度得到.
3.一次函數圖象畫法:兩點法、平移法.
例1在同一個直角坐標系中,把直線y=-2x向____平移____個單位就得到y=-2x+3的圖象;若向____平移____個單位就得到y=-2x-5的圖象.
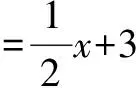
活動二:探究一次函數中k對圖象的影響.
繼續觀察圖象:
1.三條直線的傾斜度____,三個函數解析式中k值____,它們的位置關系____;
2.當k>0時,函數的圖象從左到右____,y隨x的增大而____; 當k<0時,函數的圖象從左到右____,y隨x的增大而____.
例2 已知直線y=(k-1)x+2,當k=____,該直線與直線y=2x-5平行;當k____,y隨x的增大而增大.
例3 已知點(-1,a)、(2,b)在直線y=-3x+8 上,則a,b的大小關系是____.
活動三:探究一次函數中b對圖象的影響.
在同一坐標系中用兩點法畫出以下2個函數圖象

x01y=2x-1

x01y=-x+1
(1)y=2x-1 (2)y=-x+1
一次函數常數項b對圖象的影響
圖象與y軸的交點坐標是____,當b>0時,圖象交y軸____半軸;
當b=0時,圖象經過____點;
當b<0時,圖象交y軸____半軸.
練習:1.直線y=-2x+4從左往右____,y隨x增大而____,與y軸交點坐標____,與x軸交點坐標____.
直線y=-2x+m-3與y軸的負半軸相交,則m的取值范圍____.
總結:一次函數y=kx+b圖象與性質
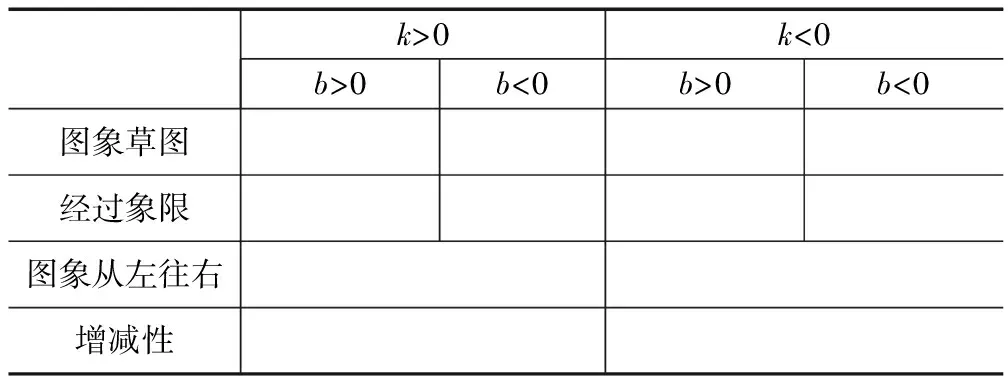
k>0k<0b>0b<0b>0b<0圖象草圖經過象限圖象從左往右增減性
練習:已知直線y=(1-3k)x+2k+1.
(1)當k為何值時,該直線經過第二、三、四象限?
(2)當k為何值時,該直線與直線y=-2x+2平行?
(3)當k為何值時,該直線與直線y=2x+5在O軸交于同一點?
四、反思
初學一次函數,學生停留在感性認識多、理性認識少,對簡單問題(直接應用圖象特征判斷問題特征等)往往能根據課堂所學的知識,再加上參考書本知識,例題練習模仿解決,通常看不出一次函數的理解程度,但隨著問題復雜化,學生對解析式與圖象的內在聯系運用呈現薄弱之勢,需后續多練多探多問,總結經驗.
不足之處:缺乏現代信息技術的運用,如幾何畫板、超級畫板的使用,能幫助學生更好地理解一次函數的圖象與性質,更深入體會數形結合思想.

