火箭發動機燃燒過程的魯棒非脆弱H∞控制*

吳玉彬，張合新，朱開銳，李國梁，惠俊軍

（1. 火箭軍工程大學控制工程系，陜西 西安 710025；2. 中國人民解放軍陸軍重慶軍代局，重慶 400060；3. 中國人民解放軍96037部隊，陜西 寶雞 721013）

時滯現象常存在于導彈的制導、飛行器的控制與航天系統當中，例如某液體火箭發動機燃燒室內的燃燒過程就包含了非常明顯的時滯，其動態模型可簡化為一個不穩定的時滯系統[1-2]。在系統的分析與控制器的設計中，如果忽略時滯的影響，往往導致系統不穩定以及性能的下降。因而近年來，時滯系統的穩定性分析及控制問題成為一個熱點的研究領域[3-7]。而對于液體火箭發動機而言，燃燒不穩定性問題一直是困擾其技術發展的難題。當發生不穩定燃燒時，燃燒室內壓力振蕩會給系統的敏感制導元件以及系統結構帶來破壞性的影響[8]。因此，如何設計反饋控制器以改善燃燒過程的穩定性能，成為學者們關注的熱點問題[9-11]。

文獻[12-14]討論了在狀態反饋控制器作用下系統的鎮定問題，但所給出的控制器都要求能夠精確實現，不具有魯棒性。在控制器的設計實現中，由于硬件和軟件等原因，不同程度上或多或少都存在一定的不確定性[15]。當控制器參數存在攝動時，常規的魯棒控制器表現出高度的脆弱性，從而造成閉環系統的性能下降甚至控制器失效。非脆弱控制[16]的提出，彌補了這一不足，它不僅考慮被控對象的不確定性，而且考慮控制器增益本身的不確定性，因而更具適應性。文獻[17-19]和文獻[20-21]分別針對時滯系統的非脆弱H∞控制問題和非脆弱保性能控制問題進行了深入研究。在這些研究中，主要圍繞如何降低所得結論的保守性和滿足一定的性能指標而展開。因此，如何選取合適的L-K泛函和界定條件，進一步得到保守性更小的時滯相關條件從而設計有效的控制器便成為目前時滯系統穩定性分析與控制綜合的首要問題。

本文中針對某液體火箭發動機的動態燃燒模型，在假定控制器增益存在加性不確定的條件下，提出一個形式簡單、保守性更低的時滯相關有界實判據。該判據借助于一種新型的時滯分割法，把時滯區間分割成不均勻的兩部分，針對每一分割區間構造新的L-K泛函，并采用新的積分不等式和交互式凸組合技術給出不包含任何多余參量的LMI形式結論。在此基礎上設計了魯棒非脆弱控制器。模擬結果表明，該控制器允許控制器增益存在一定范圍內的攝動，改善了傳統魯棒控制器的鎮定效果，具有更強的魯棒性。

1 問題描述

考慮帶有反饋伺服機構的單一燃料液體火箭發動機推進系統，系統描述見文獻[9-10]。在假定非恒穩流動并考慮一致滯后情況下，整個系統的動態方程[1-2]為：

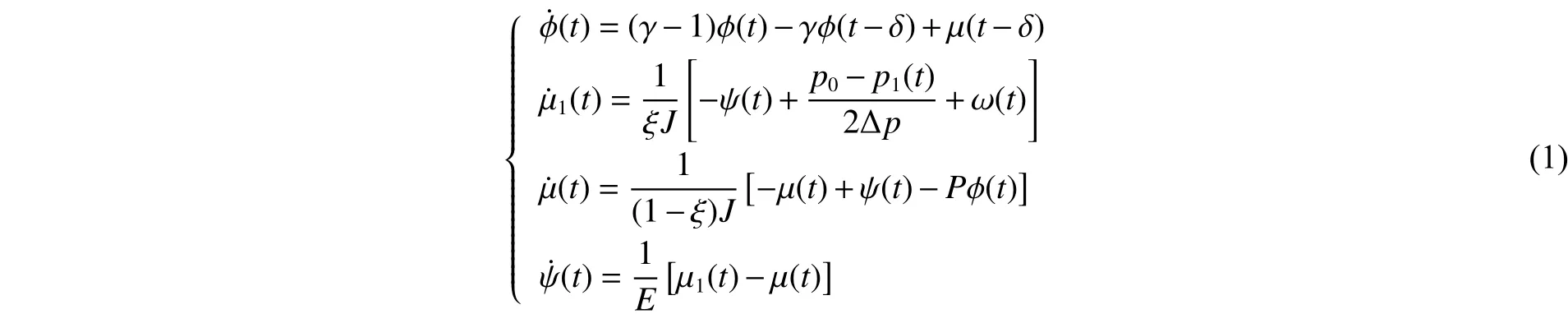
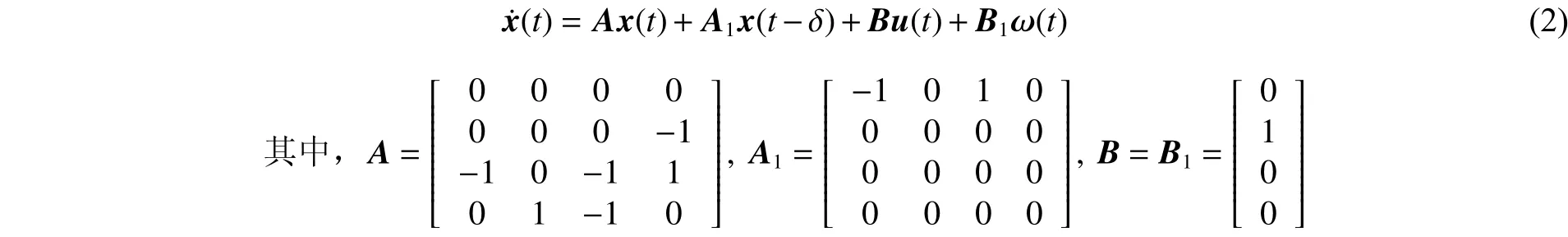
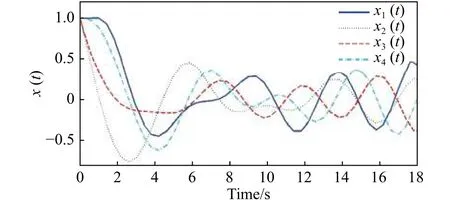
圖1 燃燒室燃燒過程的自由運動曲線Fig. 1 Free motion of combustion in chambers

針對系統(1)定義如下性能指標

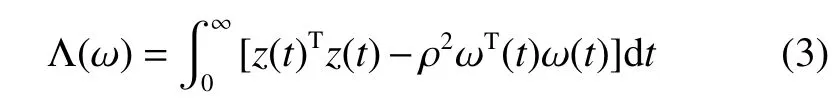
為了方便穩定性判據的證明，現將下一步需用到的引理歸納如下：

引理1[4]。假定任意的正定矩陣，標量和向量函數：，則有以下不等式成立：

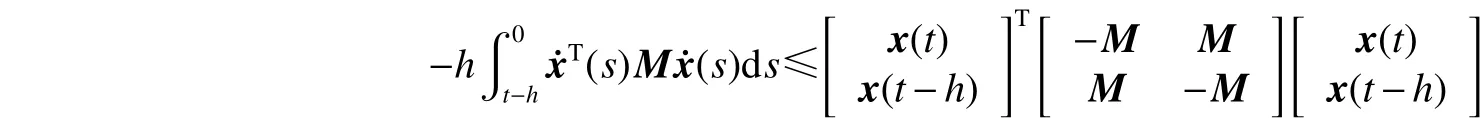
引理2[6]。假定任意的正定矩陣，標量h＞0和向量函數：，則有以下不等式成立：

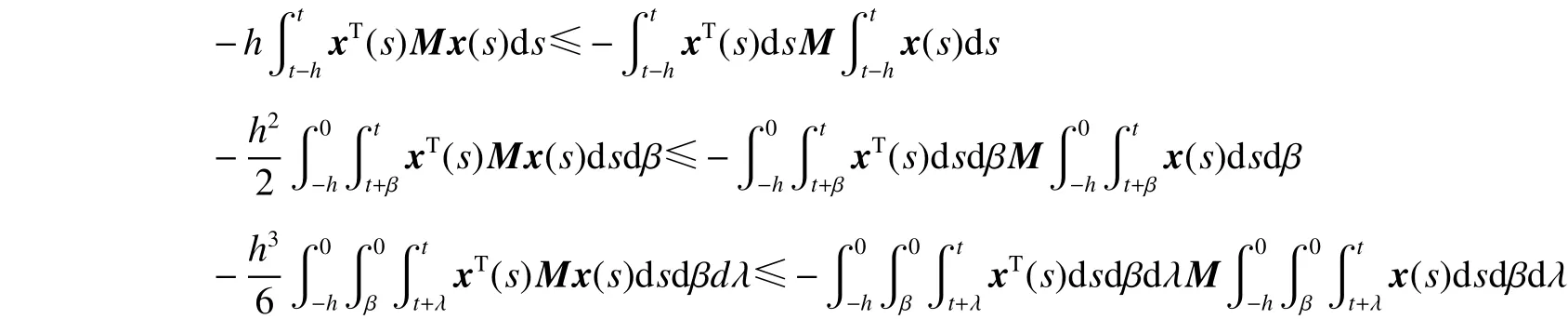
引理3[7]。假定任意的正定矩陣，標量，，向量函數：，則有以下不等式成立：

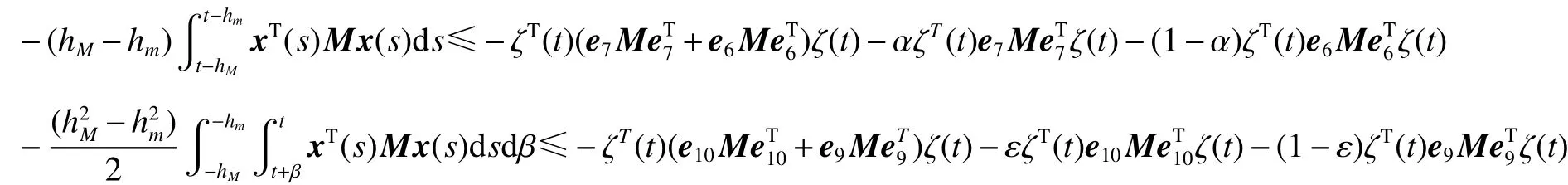
式中：

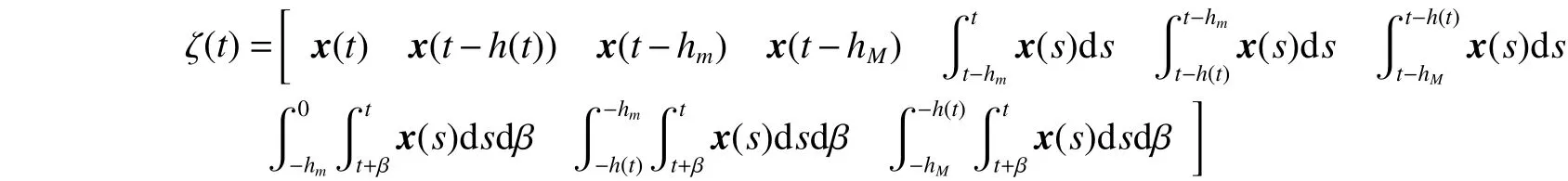
引理4[21]。給定適當維數的矩陣和，則有，對任意滿足的成立的充要條件是存在標量，使得：

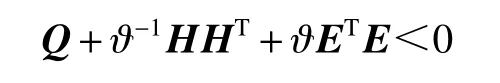
2 時滯相關有界實判據

針對系統（1）～（2），考慮如下一類具有區間變時滯的線性系統：

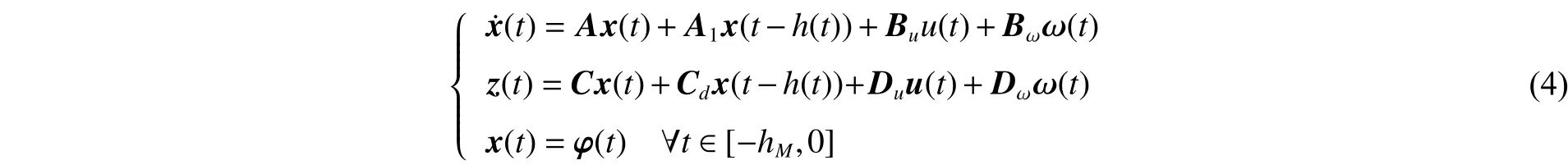
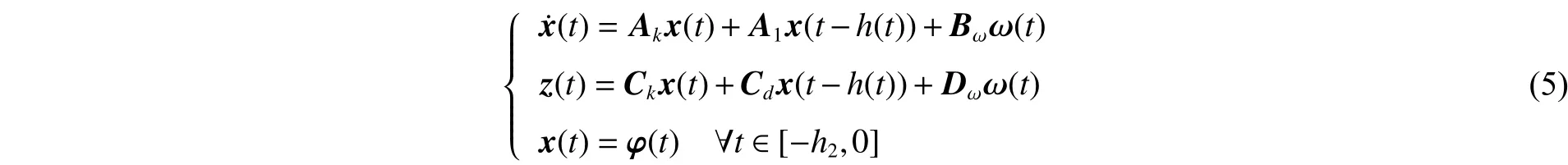
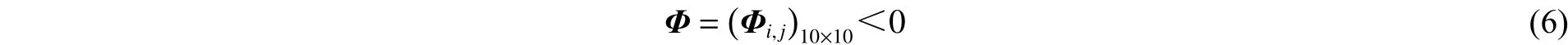
則系統(5)在非脆弱控制器(3)的作用下不僅漸近穩定，而且在零初始條件下具有給定的擾動抑制水平。

式（6）中：

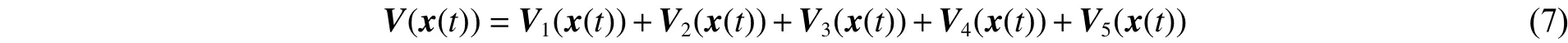
式中：

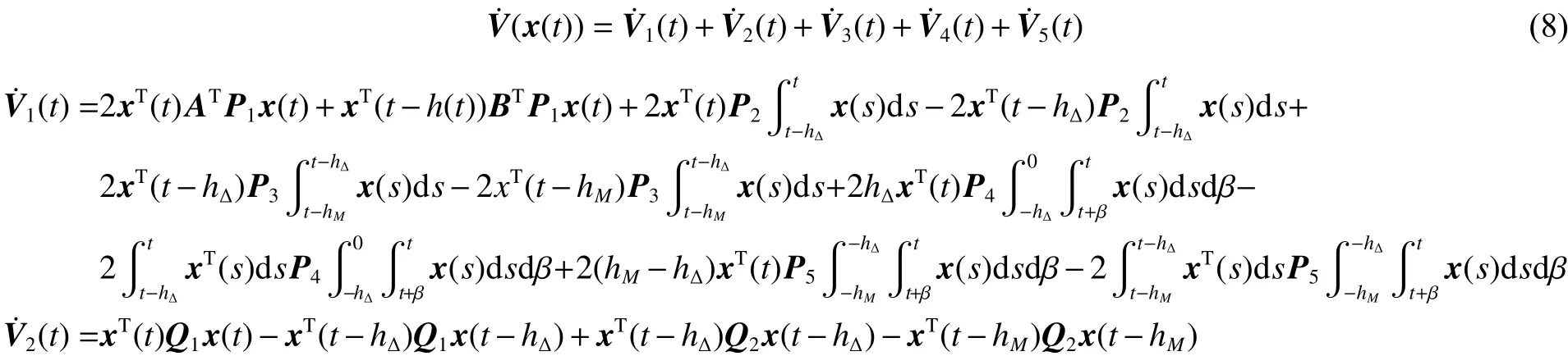
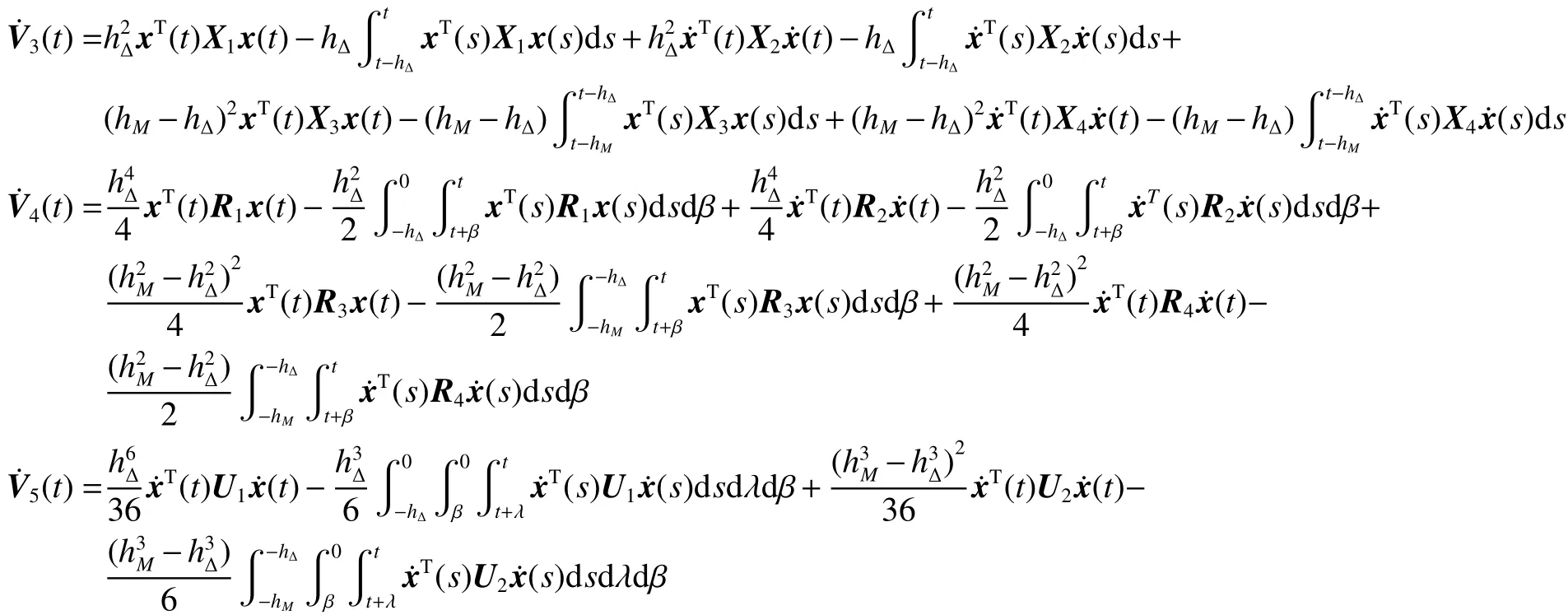
由引理1與引理2可得：

式中：

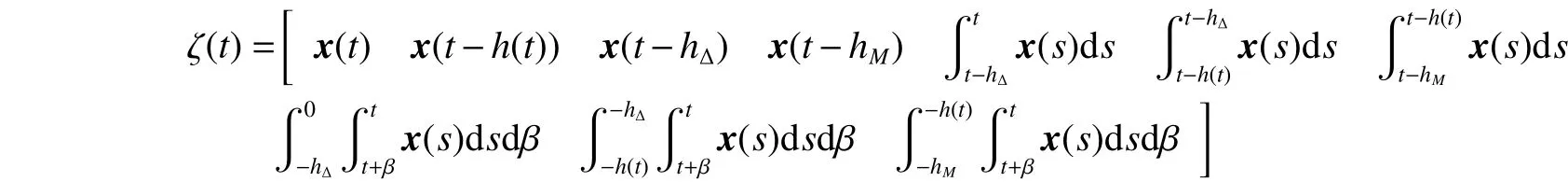
由引理3可得：

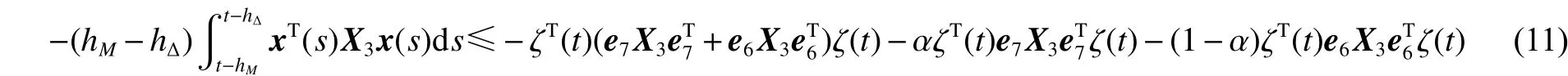
同樣可以得到：

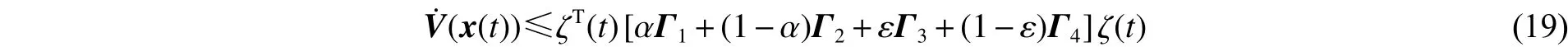
式中：

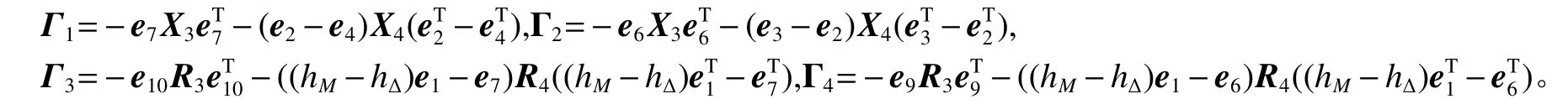
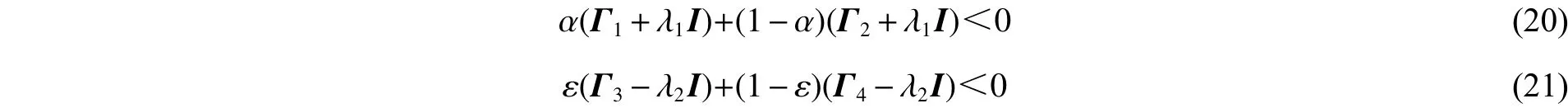
即

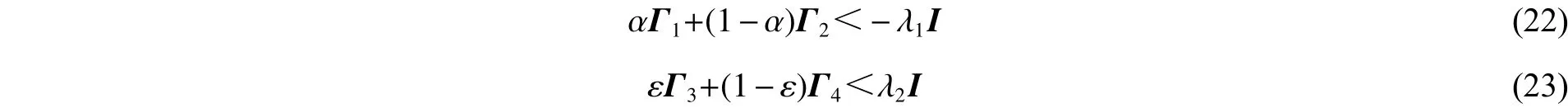
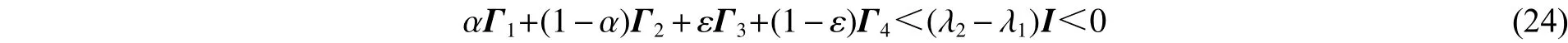
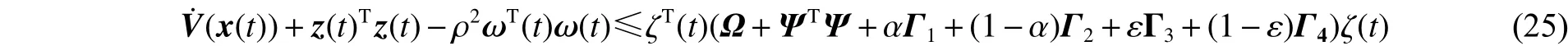
如果

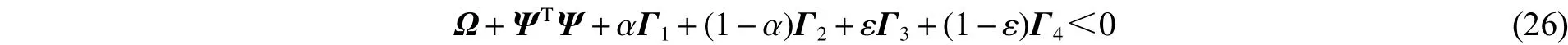
那么

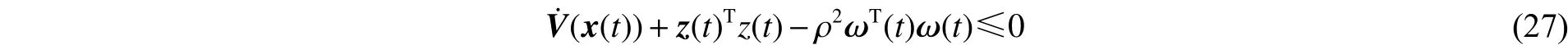
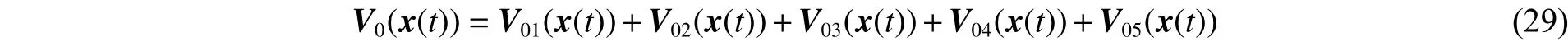
式中：

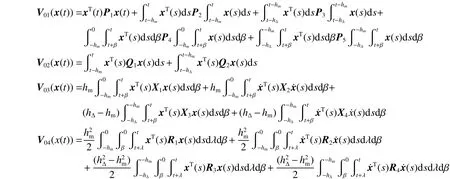
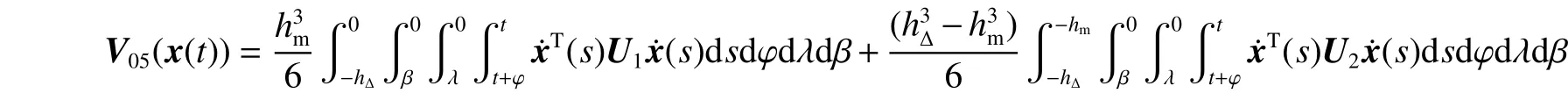
式中：

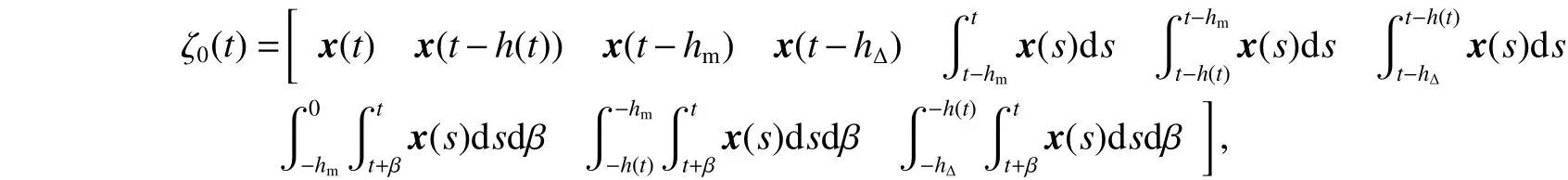
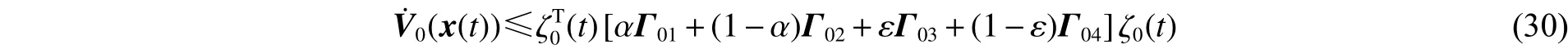
式中：

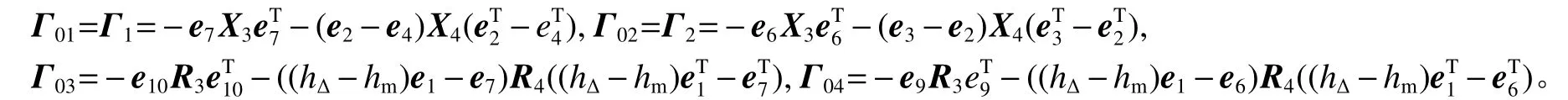
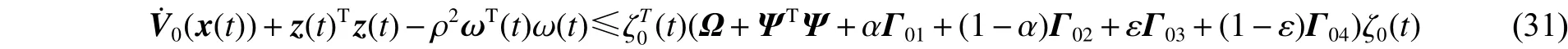
如果

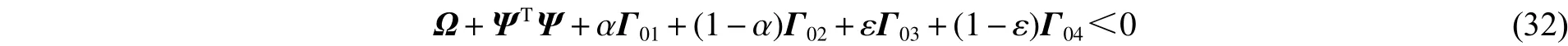
那么

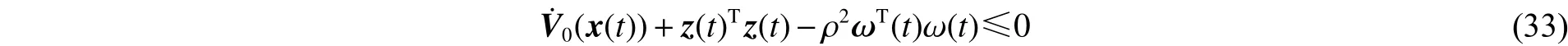
對式(19)或式(30)應用引理3，則其等價于式(6)。證畢。

針對式（1）～（2）描述的系統，考慮如下一類不確定時滯系統：

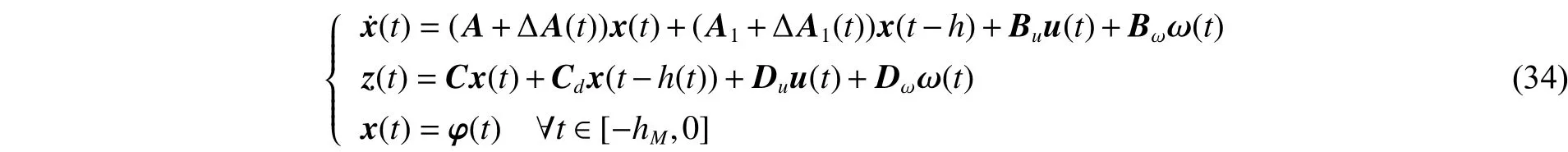
針對系統（34），本節在上一節有界實判據的基礎上，給出非脆弱控制器的設計方法。

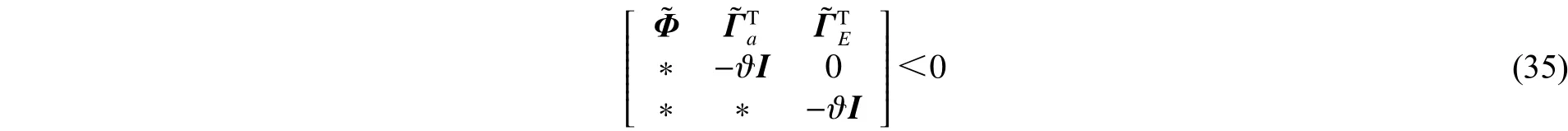
則不確定系統(34)在非脆弱控制器(3)的作用下不僅漸近穩定，而且在零初始條件下具有給定的擾動抑制水平,且控制器增益。

式中：

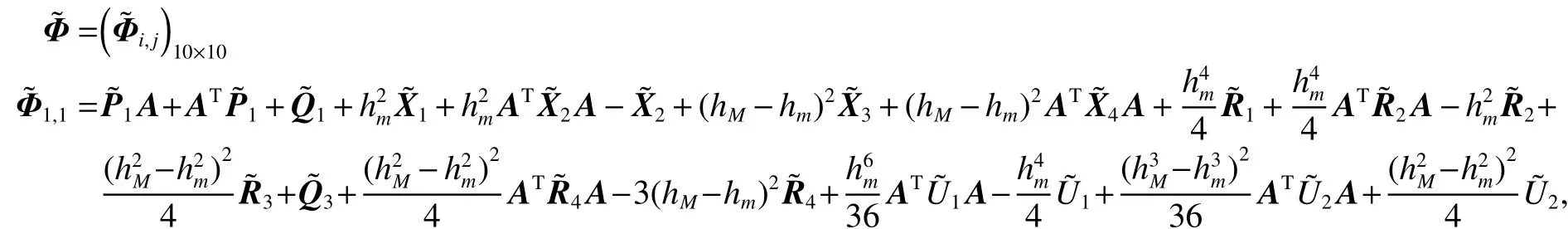
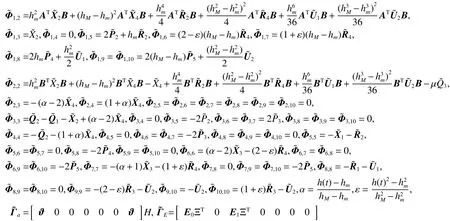
證明：由于定理1中式(6)給出的條件為非線性矩陣不等式，不能直接得到控制器的解。下面給出控制器的設計方法，首先將式(6)中的不確定項（即含項）分離，即

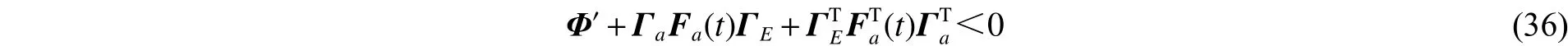
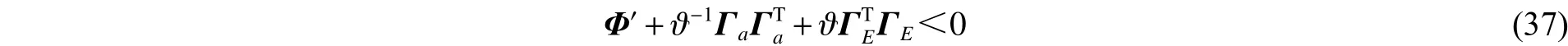
進而對式(37)應用Schur補可得

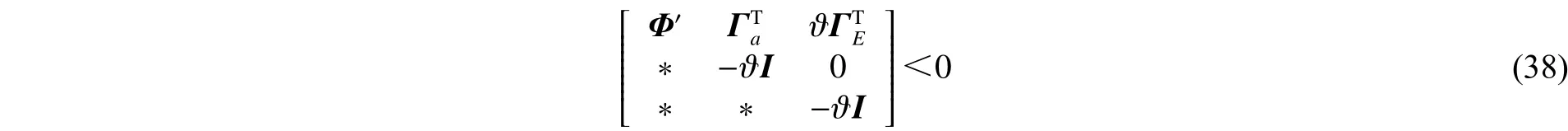
4 火箭發動機燃燒過程仿真

4.1 自由系統穩定性能分析

MADB (maximum allowable delay bound) 定義為保證系統穩定的最大允許時滯上界值，是時滯系統穩定性結論保守性最普遍的衡量標準；MAPI (minimum allowable performance index) 定義為保證系統穩定的最小允許性能指標值，是時滯系統在零初始條件下所具有的擾動抑制水平的衡量標準。

下面考慮一類具有區間變時滯的線性系統，形如式（1）所示，其系統參數如下：

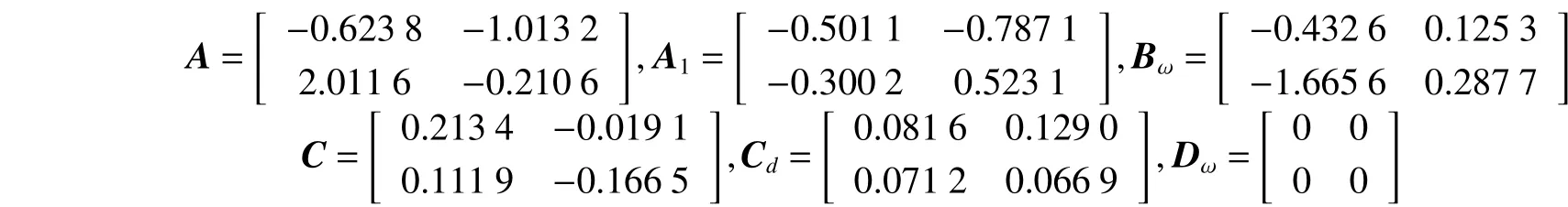
表1 不同的H 性能指標ρ，模擬給出的MADB值hMTable 1 The maximum allowable delay bound hM for a given ρ

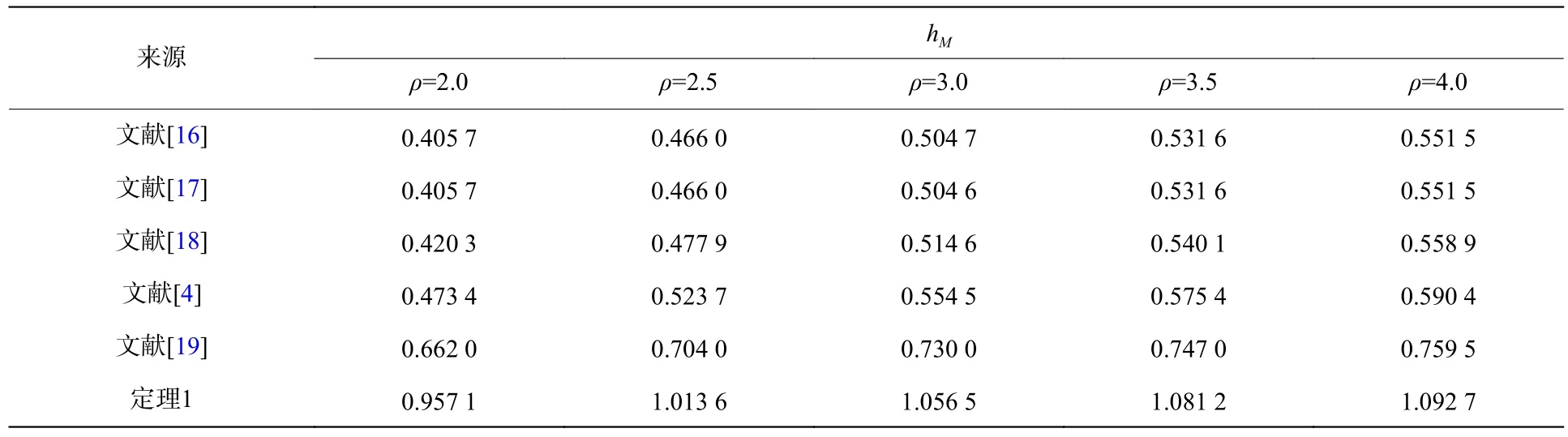
表1 不同的H 性能指標ρ，模擬給出的MADB值hMTable 1 The maximum allowable delay bound hM for a given ρ

hM ρ=2.0 ρ=2.5 ρ=3.0 ρ=3.5 ρ=4.0文獻[16] 0.405 7 0.466 0 0.504 7 0.531 6 0.551 5文獻[17] 0.405 7 0.466 0 0.504 6 0.531 6 0.551 5文獻[18] 0.420 3 0.477 9 0.514 6 0.540 1 0.558 9文獻[4] 0.473 4 0.523 7 0.554 5 0.575 4 0.590 4文獻[19] 0.662 0 0.704 0 0.730 0 0.747 0 0.759 5定理1 0.957 1 1.013 6 1.056 5 1.081 2 1.092 7來源

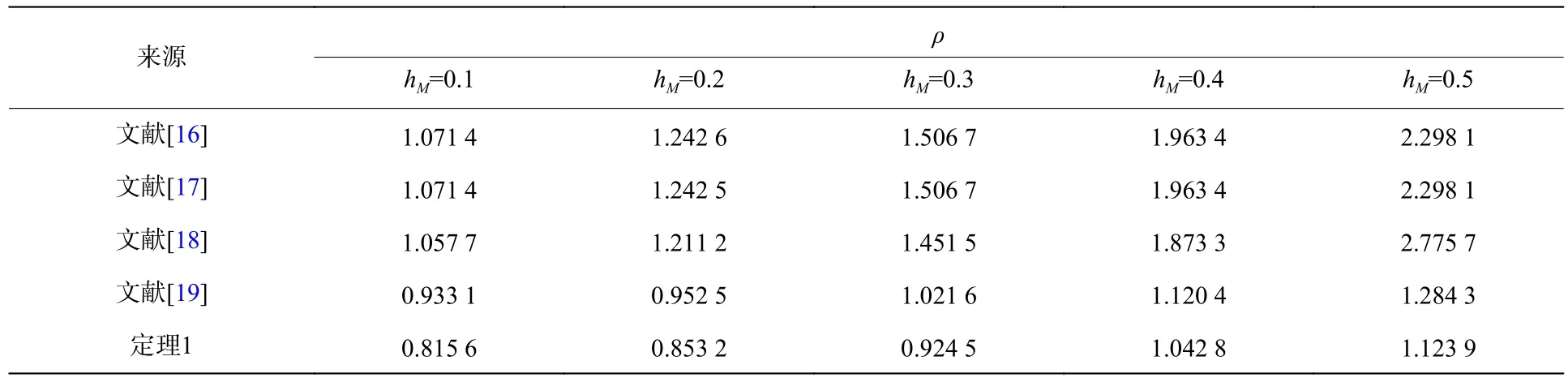
表2 不同的MADB值hM，仿真給出的MAPI值ρTable 2 The minimum allowable performance index ρ for a given hM

4.2 參數攝動的魯棒性

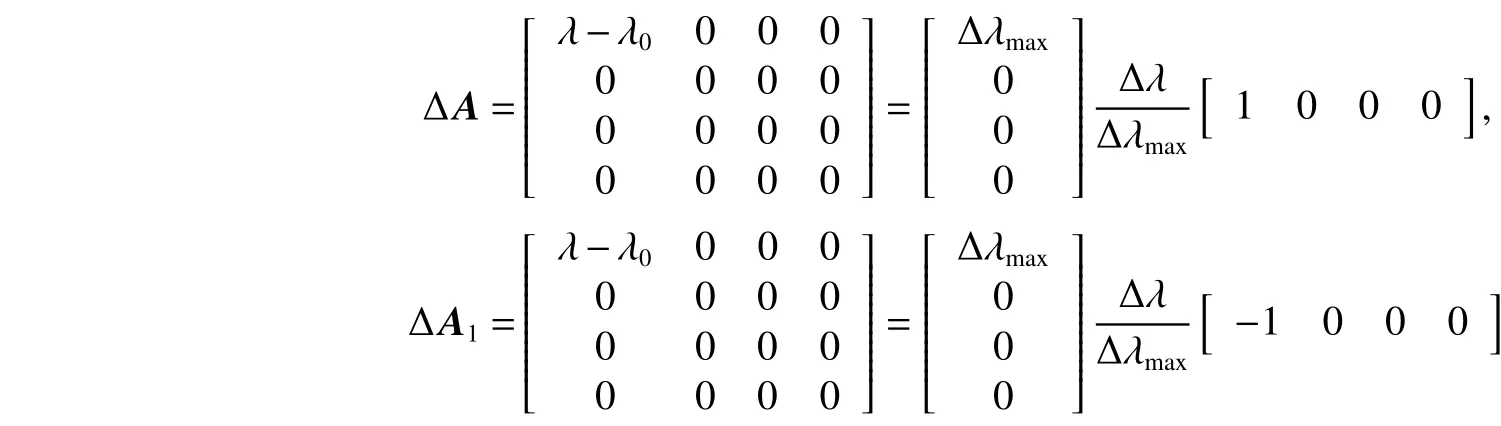
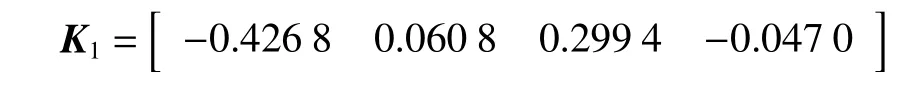
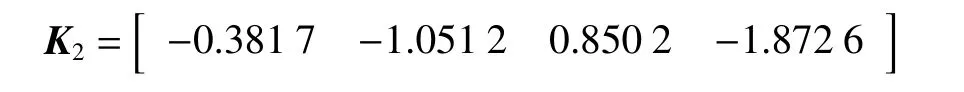
將非脆弱控制器代入燃燒過程方程，系統的狀態響應曲線如圖2所示。

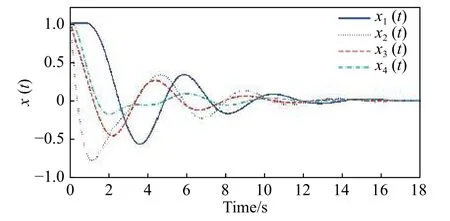
圖2 非脆弱H∞控制器作用下系統的狀態響應Fig. 2 Response of system under non-fragile H∞ controller

從圖2可知，當系統參數和控制器增益存在不確定性時，該系統不僅具有魯棒性而且是非脆弱的，燃燒過程得到了較好的鎮定，系統能滿足一定的性能指標要求，控制器具有足夠的調節余地，系統的可靠性更高。

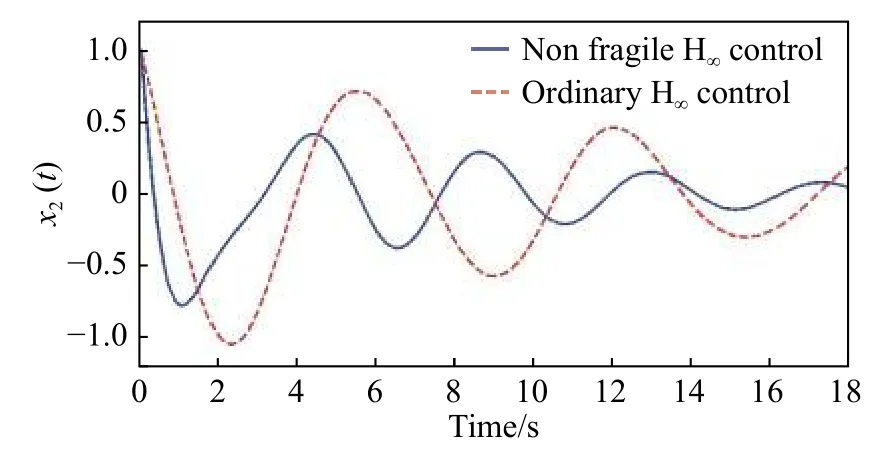
圖3 不同控制器作用下系統狀態的響應Fig. 3 Response of under different controller

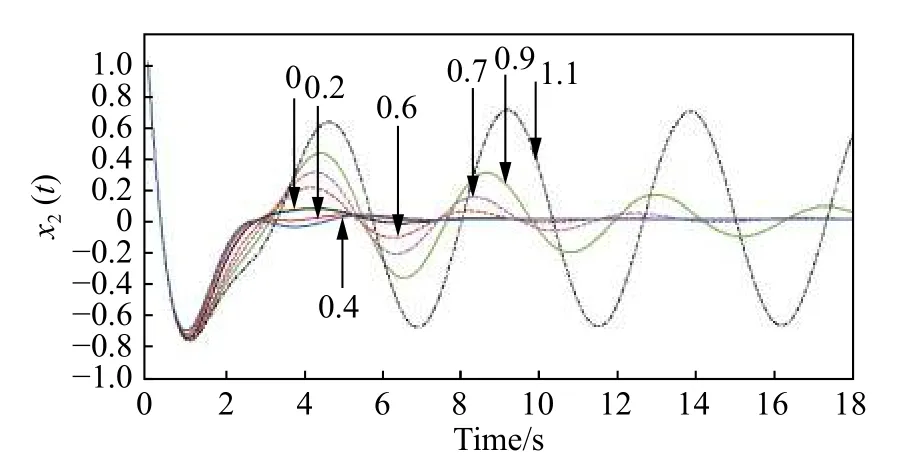
圖4 控制器對時滯參數的魯棒性Fig. 4 Robust performance of controller to variation of

5 結 論

（1）通過構造包含四重積分項的L-K泛函以及采用新穎的積分不等式來界定交叉項，給出了保證燃燒過程穩定并具有給定性能指標的時滯相關有界實引理；

（2）在有界實引理的基礎上，通過求解線性矩陣不等式的可行解來獲得控制器的參數化表達式，進而設計了一種無需參數調整并易于求解的魯棒非脆弱控制器；

（3）通過仿真實例對比驗證了所提出的時滯相關有界實引理的有效性以及所設計的魯棒非脆弱控制器的優越性。

從圖4可以清晰地看到，在本文設計控制器作用下，當時滯參數δ逐漸增大時，燃燒過程中狀態變量x2(t)逐漸趨于不穩定，但是在內，燃燒過程狀態變量x2(t)仍然是可鎮定的；需要說明的是，上面的模擬是在并且的情形下進行的，也就是說本文所設計控制器增益值滿足一定攝動性，因而提升了燃燒過程的可靠性和魯棒性。