無翼噴氣懸浮子彈藥動力特性研究

蘇新源，錢建平

(南京理工大學 機械工程學院， 南京 210094)

懸浮彈是一種“被動式”低空防御武器，采用子母彈的結構形式，母彈到達作戰區域后拋撒出子彈，子彈在空中形成一道屏障并懸浮一段時間，當敵方導彈靠近時，子彈會自動引爆，利用戰斗部的破片摧毀導彈，達到攔截的目的[1]。

噴氣反推力技術就是通過燃燒燃料或者高壓氣體存儲裝置向下噴射高速流體，獲得向上的反作用力，常用于航天飛行器、衛星以及飛機、火箭等主要推力裝置。

本文將噴氣反推力技術應用于懸浮子彈藥，設計某型懸浮彈的總體方案，研究其懸浮性能，總結其規律特性。

1 懸浮子彈藥工作原理

子彈藥結構如圖1所示，燃燒室內裝填推進劑。在子彈藥下落過程中，推進劑燃燒生成大量氣體，通過拉瓦爾噴管排出氣體并形成反推力，減小子彈藥下落速度，增加子彈藥的下落時間，達到懸浮要求。

圖1 子彈藥結構

1) 噴管推進性能

噴管是該子彈藥實現懸浮的重要裝置，其性能參數對懸浮效果具有重要影響[2]。

(1)

(2)

式中：p0為噴管入口壓強；At為噴管喉部面積；R和T為燃氣狀態參數；Γ是比熱比γ的函數：Fv為流速函數，僅與壓強比π和比熱比γ有關。

噴管喉部直徑為dt，出口直徑為de，則噴管擴張比為ξ=de/dt，其與壓強比π的關系如下：

(3)

2) 燃燒室壓強計算

推進劑開始燃燒，生成的燃氣不斷積累使壓強上升。當燃氣生成量與噴管流量平衡時，壓強也相對穩定，此時為工作壓強。推進劑燃盡，壓強隨時間迅速下降，直至與外界壓強平衡為止[3]。壓強變化過程如圖2所示的p-t曲線。

圖2 p-t曲線

燃燒室壓強-時間(p-t)曲線的微分方程：

(4)

式中：Vg為燃燒室自由容積；ρp為推進劑密度；Ab為推進劑燃燒面積；a為推進劑燃速系數；n為推進劑燃速壓強指數；φ()為沿裝藥全長的平均侵蝕比；χ為熱損失修正系數；Ψ為流量修正系數。

3) 子彈藥動力模型

子彈藥通過噴管噴出燃氣產生推力，根據動量守恒定律，可得推力F的大小為：

(5)

式中：pa為環境壓強，pe為噴管出口壓強，Ae為噴管出口面積。噴管出口壓強pe=p0·π。

整理可得：

(pa-πp0)Ae

(6)

當懸浮子彈藥在具有一定初始高度h0和初始速度v0時，懸浮裝置開始工作。由于空氣阻力較大，需考慮空氣阻力的影響，子彈藥下降高度h與時間t的關系為：

(7)

式中：m為懸浮子彈藥總重量；ρa為空氣密度；S為子彈藥橫截面積；C為空氣阻力系數。

2 懸浮子彈藥無翼噴氣動力學特性分析

當懸浮子彈藥的推力、總重量、橫截面積、工作初始高度h0和初始速度v0均確定時，可以得到高度與時間的h-t關系如圖3所示。

圖3 h-t曲線

為方便計算分析，根據懸浮子彈藥性能要求，設定子彈藥總重量為800 g，工作初始高度為1 000 m，子彈藥外徑為4 cm，要求下落時間延長10～20 s，分別得到兩種不同初速懸浮子彈藥在不同推力作用下的下落時間，其與無推力下落時間相減得到延長時間，如表1所示。

表1 不同初速、推力作用下的延長時間

由表1可得當初速為0，推力在5～6 N時可滿足條件；當初速為50 m/s時，推力需達到7～8 N。即初速越大，所需的推力也就越大。

根據前邊的式(6)可知，推力與工作壓強、噴管的尺寸有關。燃燒室壓強上升段和下降段所需時間都極端，在分析動力特性時只需考慮達到平衡時的工作壓強peq，即p0=peq。噴管喉部直徑為0.4 cm時，分別得到ξ=1.25、ξ=1.5時的推力-工作壓強(F-peq)曲線如圖4。

圖4 F-Peq曲線

從圖4可讀出一組固定工作壓強的推力數據，如表2。

表2 壓強-推力關系

ξPeq/105 PaF/NξPeq/105 PaF/N1.254.04.9841.54.04.5181.254.55.8541.54.55.4401.255.06.7251.55.06.3621.255.57.5961.55.57.2841.256.08.4671.56.08.206

從表2可以看出，在噴管擴張比一定時，工作壓強越大，推力越大；當工作壓強不變時，擴張比越大，推力越小。

由表1和表2，當初速為0時，工作壓強peq=4.5×105Pa最為合適；當初速為50 m/s時，工作壓強peq=5.5×105Pa最為合適。

同時假設處于理想狀態，即Ψ、χ、φ()均為1。此時的工作壓強可表示為

(8)

推進劑燃燒時間需大于懸浮子彈藥工作時間，推進劑采用端面恒面燃燒，藥柱長為L,燃速為μ，則：

(9)

(10)

規定推進劑藥柱直徑為2 cm，長度為3 cm，燃燒時間為30 s，D0與peq關系如圖5所示。

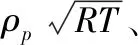
圖6 a-n曲線

為了能更符合現有推進劑的真實燃速，n∈[0.4,0.7]時的情況更為重要，其a-n曲線如圖7。

圖7 n∈[0.4,0.7]時a-n曲線

當推進劑燃速系數為3.15×10-6時，在4.5×105Pa和5.5×105Pa兩種條件下的燃速壓強指數分別為0.421 5和0.433 8。

將所有數據代入式(4)可得燃燒室壓強-時間(p-t)曲線如圖8： 從圖8可知，壓強上升段和下降段時間確實極短，可忽略不計。

將所有數據代入式(7)可得不同工作狀態下懸浮子彈藥下落高度與時間的關系如圖9。

圖8 燃燒室p-t曲線

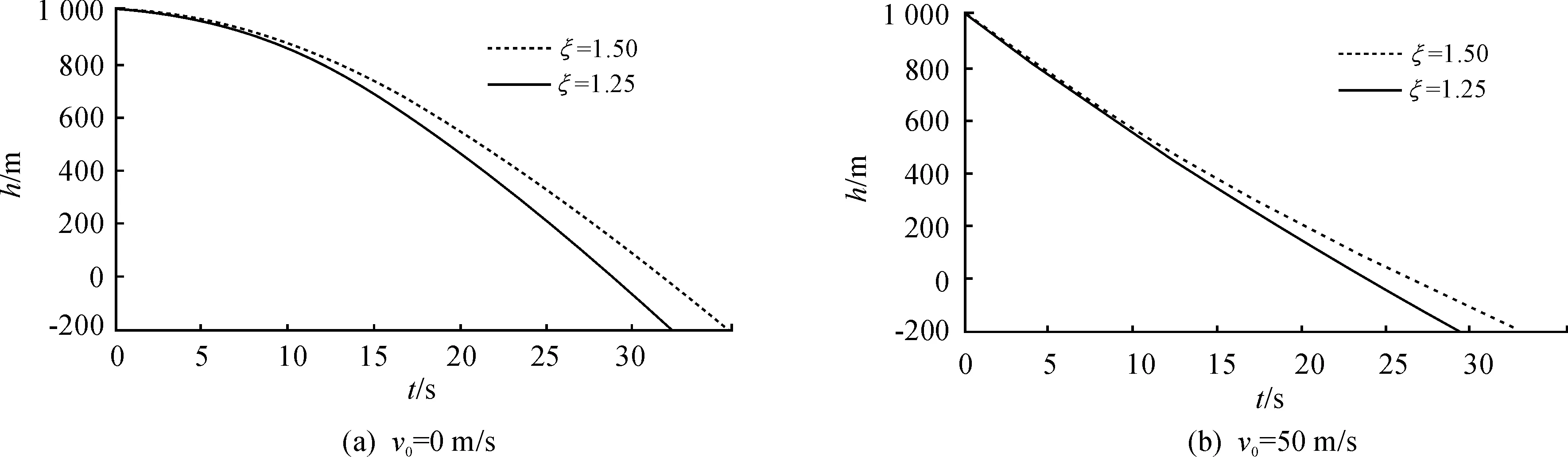
圖9 h-t曲線

各狀態下的延長時間如表3所示。

表3 各狀態下的延長時間

四種工作狀態均能滿足要求，且工作時間均小于推進劑燃燒時間。

3 噴管內流場的建模仿真分析

從前文可知，噴管的尺寸和工作狀態時決定推力大小的關鍵因素，所以需對前文所設計的噴管進行建模仿真，觀察仿真結果與理論是否符合，進行對比分析。

將噴管模型簡化為二維軸對稱問題，用ANASY ICEM CFD進行建模和網格劃分。網格劃分時采用二維結構網格生成方法，兩種不同尺寸的噴管網格劃分如圖10所示：

圖10 網格劃分

將網格導入FLUENT進行仿真，選擇二維求解器，視為可壓縮流動，忽略粘性力對流動的影響，入口壓力為絕對壓力。

仿真結果與分析如圖11～圖13所示。

求得出口等效壓強與理論結果如表4所示：由表4可見，當ξ=1.25時，理論結果與仿真結果幾乎相同；當ξ=1.5時，因為噴管長度增加，能量損耗更大。由于理論分析是在假設為理想條件下進行的，理論結果與仿真結果有所差距，但誤差不大。

此外，出口壓強分布狀態與peq無關，與ξ有關。可能因為噴管擴張段長度不同，出口部分壓力波的傳輸與疊加情況不同。

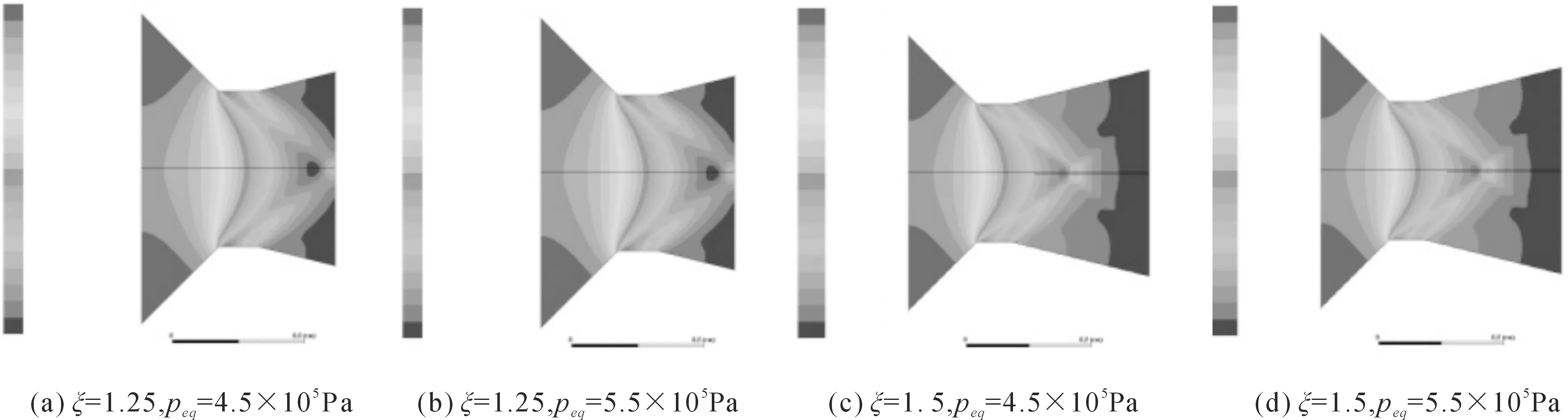
圖11 噴管內部壓力云圖

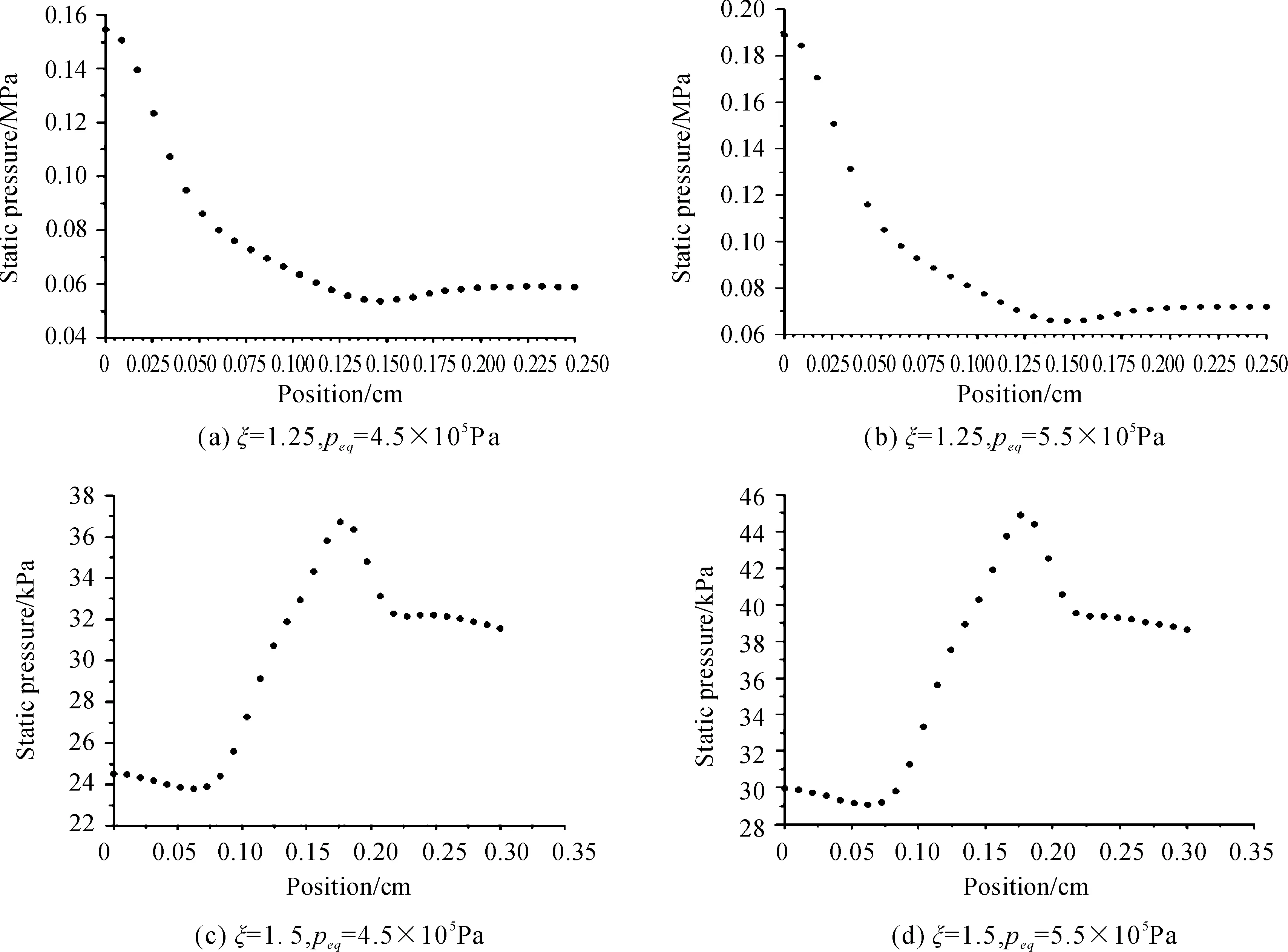
圖12 出口處壓力隨位置變化曲線

圖13 出口壓力仿真計算結果擬合曲線

表4 出口等效壓強

4 結論

1) 可以通過合理設計噴管尺寸，選定相關參數復合要求的推進劑，實現懸浮子彈藥的無翼噴氣懸浮。

2) 懸浮子彈藥初始降落速度越小，噴管擴張比越小，延時效果越好。

4) 燃燒室壓強變化的上升段和下降段時間極短，可以忽略不計。

5) 噴管長度越長，仿真結果與理論誤差越大，需在理論計算時考慮能量損耗。