二元機翼的非線性氣動彈性主動控制

張忠源,段靜波,史鳳鳴， 路 平

(1.陸軍工程大學石家莊校區 無人機工程系, 石家莊 050003； 2.石家莊鐵道大學 工程力學系， 石家莊 050003)

氣動彈性主動控制是近幾十年發展起來的試圖解決飛行器結構不穩定和疲勞問題的關鍵技術[1]。機翼的氣動彈性特性尤其是機翼的顫振為最嚴重的動不穩定現象，會使機翼從氣流中吸收能量導致結構振動，甚至導致結構嚴重破壞。學者一直在探索延緩和控制顫振的各種途徑，現有途徑大致分為兩類：被動控制和主動控制，被動控制是已廣泛應用的技術，主動控制是為了彌補被動控制的不足，是一種新技術。目前，研究最多的是氣動彈性主動控制。

20世紀90年代鄒叢青等[2]開始了飛行器顫振主動控制問題方面控制律的研究，把最優控制理論和顫振分析的狀態空間法相結合，解決了陣風緩解和穩定裕度等問題。宗捷等[3]針對某一特殊無人機機型開始了陣風問題和顫振主動控制的研究，應用現代控制理論對飛行器系統分別作開環和閉環分析，設計的控制律具有減緩陣風響應和抑制顫振的雙重效果。M Tadi[4]研究了用于氣動彈性系統中顫振抑制的反饋控制設計，推導了基于狀態相關Riccati方程的反饋控制律。M Karpel[5]使用狀態空間氣動模型設計一個恒定增益的反饋控制系統，該系統可同時保證穩定性和完成對整個飛行包線內陣風響應參數的優化。多輸入/多輸出系統的氣動彈性主動控制問題成為氣動彈性分析的重要研究方面，吳志剛[6-7]團隊以無人機二元機翼和帶兩個控制面板的三角機翼為研究對象，將滑模控制理論和LQC理論用于解決氣動彈性主動控制。隨著現代控制科學的發展，王囡囡等[8]提出了基于動柔度法的顫振主動控制研究，該方法無需提前知道機翼的剛度、阻尼等參數，可根據極點控制理論確定系統反饋控制增益。而真實的氣動彈性控制系統是非線性的[9]，非線性系統更加復雜，求解難度更大，SH Moon等[10]基于非線性氣動模型進行了最優控制設計的探索。A Behal等[11]研究了在不可壓縮流場中的非線性二維機翼系統的自適應控制。丁千等[12]針對具有非線性俯仰剛度的二元機翼研究了顫振主動控制。考慮機翼俯仰方向阻尼和剛度存在非線性情況，許行之等[13]采用多項式非線性模型建立機翼控制模型，利用李雅普諾夫穩定性理論實現機翼的氣動彈性自適應控制。

本文對機翼非線性主動控制進行了拓展研究。以二元三自由度機翼為研究對象，建立了機翼的非線性氣動模型，得到時變控制系統。針對時變系統控制律設計困難問題，結合系統時變規律，設計了對應的狀態反饋控制律，為解決非線性氣動彈性控制問題提供了新思路。

1 三自由度二元機翼非線性氣動模型

如圖1所示，在機翼后緣有一控制面。系統的三自由度分別為剛心E的撓度h(向下為正)、機翼繞剛心的扭轉角為α(迎風抬頭為正)以及控制面偏轉角β(向下偏轉為正)。機翼的運動方程為：

(1)

式中：m為單位長度機翼的質量；Sα為單位展長機翼對彈性軸的質量靜矩；Iα是單位展長機翼對彈性軸的質量慣性矩；Kh、Kα分別為機翼沉浮和俯仰剛度。機翼所受的升力L和力矩M可以表示為:

(2)

這里升力L和力矩M都由兩個部分組成，Ll和Ml表示線性部分，表達式為：

(3)

圖1 三自由度二元機翼

Ln和Mn表示非線性部分，這里采用文獻[14]中介紹的ONERA動態失速模型，表達式為：

(4)

需要說明的是，非線性氣動系數下標z=L表示與升力有關系數；下標z=M表示與力矩有關的系數。非線性氣動系數Cz表達式如下：

(5)

非線性氣動力部分的有關參數有r1z，r2z，r3z為：

為簡化計算，通常用折線代替靜態空氣動力曲線，如圖2。

圖2 靜態空氣動力曲線

(7)

為通過式(5)求解出非線性氣動系數Cz，本文采用Laplace變換得方法，將式(5)進行Laplace變換并整理得：

(8)

通過Laplace逆變換可以得出：

(9)

分別令z=L和z=M代入式(4)并聯立式(1)、式(2)、式(3)即可得到機翼的三自由度二元機翼非線性氣動模型。

2 狀態空間模型與控制律設計

把上一節得到的機翼非線性氣動模型改寫成狀態空間形式：

(10)

圖3 參數k2時間響應波形

針對系統的特征，將本文控制系統設計成狀態反饋系統，K為反饋矩陣，系統矩陣變為(A-BK)，如圖3所示，橫坐標t=t+時，時變參數幅值為最大值，此狀態對應的系統相關矩陣表示為A+、B和K+，橫坐標t=t-時，時變參數幅值為最小值，此狀態對應的系統相關矩陣表示為A-、B和K-，這兩種狀態結合李雅普諾夫判據可以得出：

(11)

定義折合系數ε，且ε∈(0,1)，將式(11)中兩個不等式兩邊分別乘以系數ε和(1-ε)并相加，得到：

P([(1-ε)A-+εA+]-B[(1-ε)K-+εK+])<0

(12)

式(12)表示含有折合系數ε的新系統，且符合李雅普諾夫穩定性判據，此系統對應的相關矩陣可以表示為：

A(ε)=(1-ε)A-+εA+

(13)

K(ε)=(1-ε)K-+εK+

(14)

由于A+、A-、K-和K+為系統時變參數取最值對應的解，所以A(ε)、K(ε)可以表示出在整個時域范圍內的系統所有滿足李雅普諾夫穩定性判據的系統矩陣。任意時刻t0的狀態反饋矩陣K(t0)求解過程如圖4所示。

圖4 反饋控制求解流程

圖4說明了本文求解某一時刻反饋矩陣K(t0)具體步驟，由于直接運用解析法求解時變系統的反饋控制矩陣很難實現，本文采取建立時刻t0與折合系數ε的一一映射關系的方法來實現對K(t0)的求解。需要說明的是在運用式(11)求解K-和K+時，要借助線性矩陣不等式(LMI)工具箱，一個線性矩陣不等式問題一旦確定，就可以通過調用適當的線性矩陣不等式求解器來對這個問題進行數值計算。

整個機翼的狀態反饋系統流程如圖5所示，時變系統通過引入時鐘信號實現對時變矩陣A(t)的表示，而后計算反解出折合系數ε，進而求出對應時刻的反饋矩陣K(t)，從而實現對系統的反饋控制。

圖5 控制系統流程

3 算例仿真與分析

本研究選取的三自由度二元機翼模型的具體參數如表1。

表1 機翼模型參數

已知機翼的開環顫振速度為29.3 m/s，仿真時選取的空速為33.7 m/s(高于開環顫振速度的15%)，使用上一節設計的反饋控制系統，具體參數見附錄，先仿真得到系統的開環時域響應，如圖6所示。

圖6 開環時域響應

圖6分別是機翼撓度和扭轉角隨時間的變化曲線，從仿真的結果可以看出，在開環系統條件下，風速為33.7 m/s時，此時風速高于機翼顫振速度，系統呈現振蕩發散的狀態。隨后，接入反饋控制模塊，在同樣的風速下，仿真得到系統的閉環時域響應，如圖7所示。

通過觀察圖7的機翼撓度和扭轉角隨時間的變化曲線，可以看出閉環控制系統是穩定的，系統在0.8s左右可以收斂至平衡位置，從而改善了機翼系統的氣動彈性特性，提高了機翼安全飛行速度上限。當機翼受陣風干擾時，會因為外界干擾力作用而發生強迫運動，對機翼結構強度、疲勞以及飛行品質產生較大影響。這里主要討論控制系統對陣風作用下機翼響應的影響。以“1-cos”陣風為例，因為實際工程中這類陣風遇到的頻率最高，“1-cos”陣風速度表達式為：

(15)

其中：W0表示陣風峰值速度，取20 m/s；H表示離散尺度，取4 m。陣風的具體形式如圖8所示。

圖7 閉環時域響應

圖8 “1-cos”陣風

分別計算開環系統和閉環系統在“1-cos”陣風影響下的機翼撓度響應，其中空速V=25 m/s，選取的空速低于機翼的顫振速度，也就是說此時機翼系統本身處于穩定狀態，當遇到突風產生激勵，機翼系統通過自身調節可以恢復穩定，得到的響應結果如圖9所示。

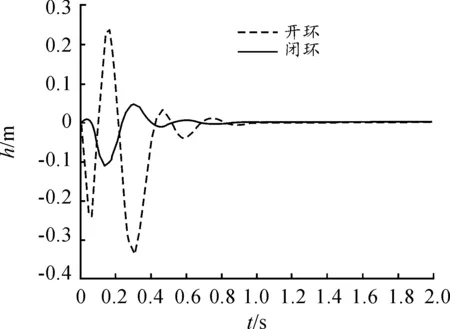
圖9 機翼陣風響應結果

從圖中對比開環系統和閉環系統的陣風響應，可以看出閉環控制系統相對于開環控制系統，有效降低了機翼振幅，同時縮短了機翼響應衰減時間，大大提高了機翼系統的穩定性，保證了機翼氣動彈性特性和飛行品質。

4 結論

1) 針對時變系統控制律設計困難問題，結合系統時變規律，設計了對應的狀態反饋控制律。

2) 通過仿真對比開環和閉環系統的超顫振速度條件下時域響應、陣風響應，表明設計的反饋控制律可以有效地改善機翼氣動特性。