扭桿油氣復合懸掛特性研究

代健健，毛 明，陳軼杰，張亞峰，杜 甫

(中國北方車輛研究所， 北京 100072)

履帶車輛懸掛系統是履帶車輛實現機動性的重要組成部分。現階段，國內外高機動履帶車輛懸掛系統主要采用扭桿懸掛和油氣懸掛[1]。扭桿懸掛具備制造簡單、工藝成熟、可靠性高等優點，但由于剛度幾乎不變，導致其對路面的適應性較差。油氣懸掛具有明顯的非線性、變剛度等優點，具有較好的路面適應能力，但油、氣密封可靠性差和溫升導致的懸掛特性及車姿變化。在實際工程中，扭桿彈簧的故障主要是由于過載或疲勞而斷裂，油氣彈簧的故障主要是由于溫升過載或疲勞引起密封失效和車姿變化。

為提高履帶車輛機動性和可靠性，一些科研院校開展了一系列研究及探索[2-6]，例如：內蒙古一機集團研發了高強度扭桿彈簧新材料，使扭桿最大許用應力超過1250MPa，從而提高了扭桿懸掛的性能和可靠性；中國北方車輛研究所積極開發各型油氣懸掛，已應用在多種輕中型履帶車輛上。為提高主戰坦克的機動性能和行動系統的可靠性，2017年，中國北方車輛研究所提出了將扭桿彈簧和油氣彈簧并聯的復合懸掛的構型設想，相對扭桿懸掛能提高懸掛系統的性能，又能滿足扭桿彈簧和油氣彈簧的可靠性要求，本研究就是針對這種新構型的復合懸掛開展特性建模及其載荷匹配對特性的影響規律研究。

1 復合懸掛彈性特性

本文以某型履帶車輛為研究對象，旨在提高其行駛平順性，使乘員獲得更舒適的駕乘感受，以進一步提高越野速度。考慮到實際過程中扭桿彈簧與油氣彈簧的失效形式，綜合各自優勢，將油氣彈簧取代減振器，并承擔扭桿懸掛部分載荷，起到儲能和減振的作用。考慮到履帶車輛懸掛空間布置要求及彈性元件技術成熟度，設計了如圖1所示的扭桿油氣復合懸掛，在該模型中，油氣彈簧上鉸支點和扭桿固定端與車體連接，下鉸支點通過平衡肘上的銷耳與平衡肘連接。

圖1 扭桿—油氣復合懸掛三維圖

工作原理圖如圖2，H為車底距地高，E為平衡肘轉動中心與車底距離，HL為履帶板高度，D為負重輪直徑，δ為輪緣變形量，R為平衡肘轉動半徑，r為拉臂OB的長度，l為油氣彈簧任意位置的長度，α為平衡肘與水平線的夾角。

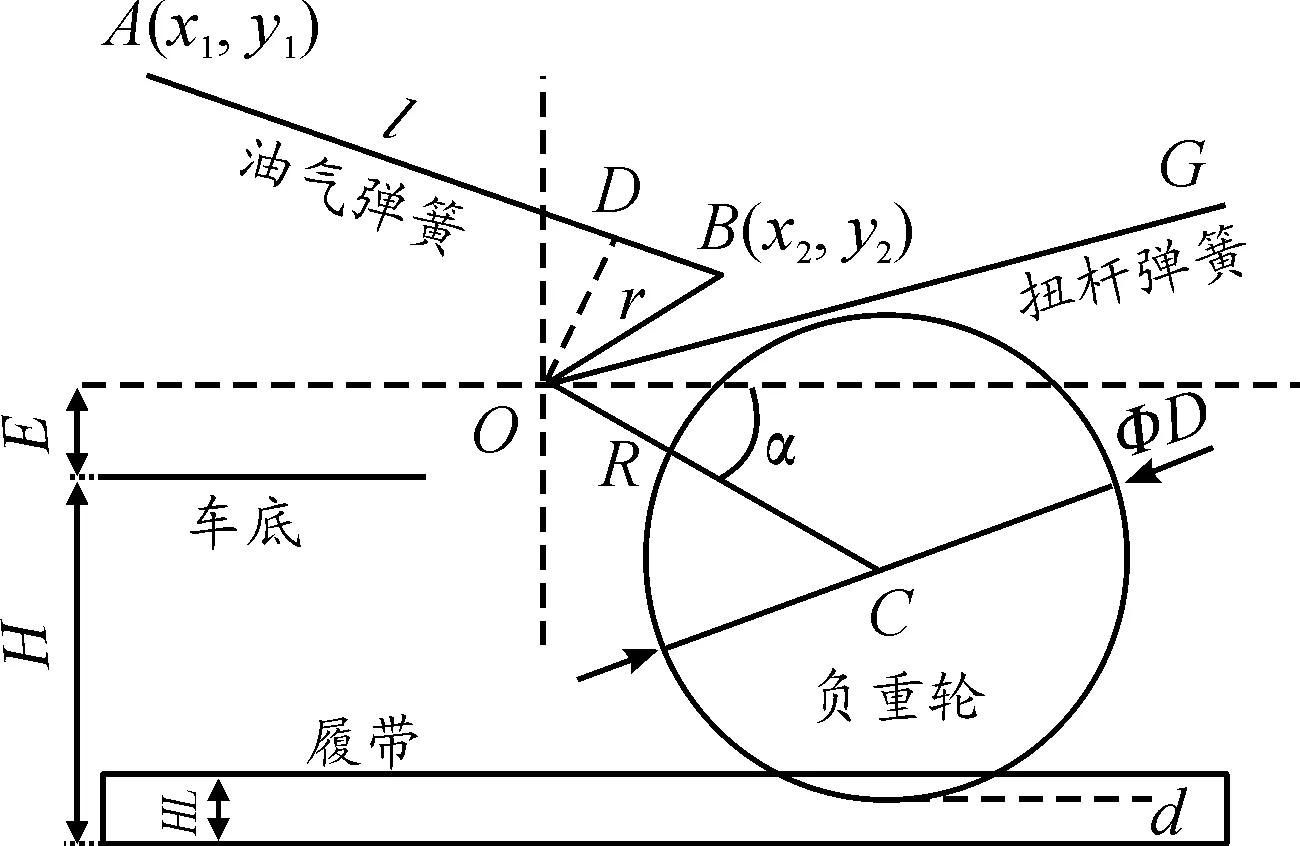
圖2 復合懸掛工作原理圖

在壓縮行程時，負重輪帶動平衡肘逆時針轉動，扭桿彈簧與油氣彈簧儲存能量，將動能轉換為勢能，同時油氣彈簧產生一定阻尼力，轉換為熱能；在復原行程時，扭桿彈簧與油氣彈簧釋放能量，推動平衡肘順時針轉動，將勢能轉換為動能，同時油氣彈簧產生較大阻尼力，將動能轉換為熱能。

由于阻尼力僅由油氣彈簧承擔，其減振閥的設計方法等同于純油氣懸掛的減振閥的設計方法，因此復合懸掛的阻尼特性與油氣懸掛的阻尼特性相同。

1.1 彈性特性數學建模

復合懸掛同時采用扭桿懸掛和油氣懸掛，必然涉及承載力分配的問題，靜平衡位置扭桿懸掛和油氣懸掛各自承擔靜載荷的大小對懸掛參數及特性有重要影響，如：油氣彈簧初始充氣壓力、扭桿彈簧工作直徑等參數會根據承載力進行初步設計。引入靜載荷分配系數λ，對靜平衡位置時二者承擔的靜載荷進行分配，λ定義為扭桿懸掛靜載荷與懸掛系統靜載荷的比值。若單輪靜平衡位置承載力為Ffj，則扭桿懸掛靜載荷Fnj=λFfj，油氣懸掛靜載荷Fyj=(1-λ)Ffj。

初步設計時，以車底距地高H、負重輪動行程fd等參數作為設計輸入，假定油氣彈簧主活塞與浮動活塞橫截面積相等，油氣彈簧氣體為理想氣體。

1.1.1 扭桿懸掛彈性特性

負重輪行程f與α的關系：

f=R(sinαj-sinα)

(1)

式中，αj為平衡肘位于靜平衡位置時與水平線夾角，αj=arcsin[(H+E-HL-0.5D+δ)/R]。以靜平衡位置為零點，規定靜平衡位置向上為正，向下為負。

扭桿直徑d為扭桿彈簧最關鍵的參數，應當滿足最大剪切應力τmax小于許用剪切應力[τmax]：

(2)

式中：d為扭桿直徑；Gt為扭桿材料剪切模量；L為扭桿工作長度；W為扭桿材料抗扭截面系數，W=πd3/16；θmax為扭桿最大扭轉角。

在fd一定的條件下，扭桿扭轉到最大角度時平衡肘與水平線的夾角α1：

α1=arcsin[(H+E-HL-0.5D+δ-fd)/R]

(3)

扭桿彈簧的靜扭矩Mj：

(4)

式中：θj為扭桿從初始安裝位置扭轉到靜平衡位置的扭轉角，即靜扭角。可得扭桿靜平衡位置剪切應力τj=Mj/W。

靜扭角θj與θmax、α1、αj的關系：

θj=θmax-(αj-α1)

(5)

綜合式(2)～式(5)，可推出d與[τmax]的關系：

(6)

在設計d時，將標準系列直徑d代入式(6)，可驗證d是否滿足強度條件，若不滿足，說明在該直徑下，扭桿將會發生斷裂；若任意d都不滿足要求，則說明設計的動行程fd過大。

平衡肘初始安裝角α0=αj+θj，將其代入式(1)可得負重輪靜行程fj。

扭桿懸掛彈性力Fn[1]：

(7)

扭桿懸掛剛度系數Kn[1]:

1.1.2 油氣懸掛彈性特性

懸掛杠桿比I=|OD|/Rcosα，|OD|為平衡肘轉動中心距油氣彈簧上、下鉸支點中心線的距離，靜平衡位置杠桿比Ij=|OD|j/Rsinαj。

對于油氣彈簧，在設計時通常使靜平衡位置的壓強在某值Pj0附近較為合適，可根據Fyj和Ij推出理論上的浮動活塞直徑dh0，根據國家標準選取相對應的標準浮動活塞直徑dh。

根據標準dh求出靜平衡位置的壓強Pj=Fyj/(Ij·Ah)。

根據理想氣體狀態方程[7-8]：

(常數)

(8)

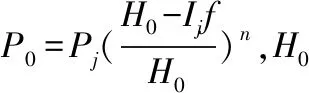
任意位置油氣彈簧壓強P：

(9)

式中：lmax為油氣彈簧上下鉸接點最長距離(位于初始安裝位置時)；l為任意位置油氣彈簧上下鉸接點距離。

油氣懸掛彈性力Fy：

Fy=Ah(P-Pa)I

(10)

油氣懸掛剛度系數Ky:

(11)

因此，復合懸掛彈性力Ft=Fn+Fy。復合懸掛剛度系數K=Kn+Ky。

1.2 復合懸掛性能參數

復合懸掛的性能參數涉及緩沖可靠性和行駛平順性兩個方面。緩沖可靠性表示彈性元件的疲勞強度儲備，常用動比位能Ed來評價。行駛平順性表示對地面不平度的隔振性能，常用自由振動周期Tj來評價。

動比位能Ed[9]：

(12)

自由振動周期Tj[9]：

(13)

式中：m為簧上質量；Kj為靜平衡位置復合懸掛剛度。

動比位能越大，表示坦克裝甲車輛彈性元件吸收振動能量的能力越強。在負重輪行程一定的條件下，動比位能越大，要求彈性元件剛度越大，但剛度越大，會使自由振動周期越小，車輛行駛平順性越差。因此，復合懸掛的性能參數Ed和Tj是一對矛盾參數，只能折中設計。

1.3 仿真分析

根據懸掛布置空間及密封件性能等方面的約束，初步設計復合懸掛部分參數如表1所示。

編程仿真分析可得油氣懸掛、扭桿懸掛、復合懸掛的彈性特性曲線和剛度特性曲線，如圖3、圖4所示。

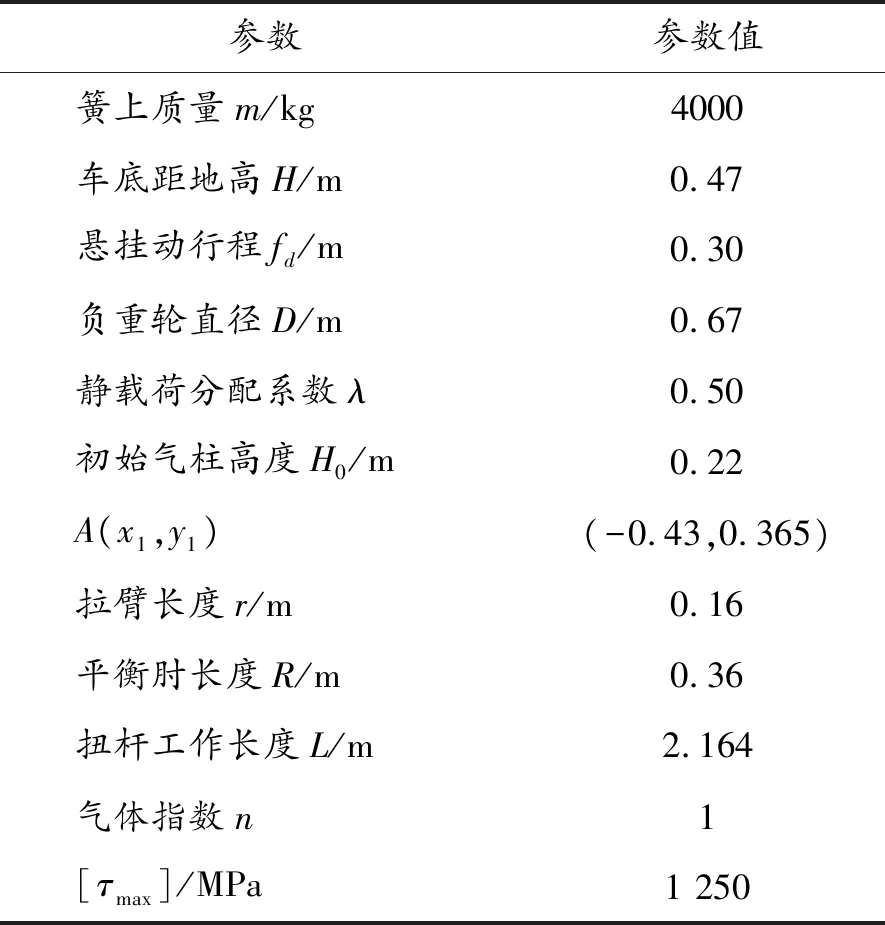
表1 部分設計參數

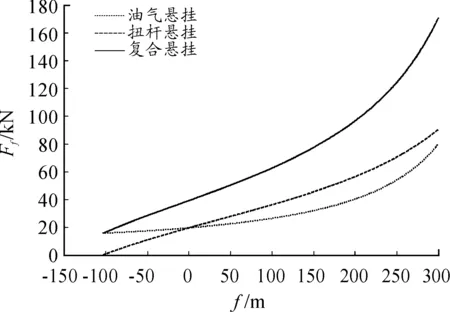
圖3 復合懸掛彈性特性曲線

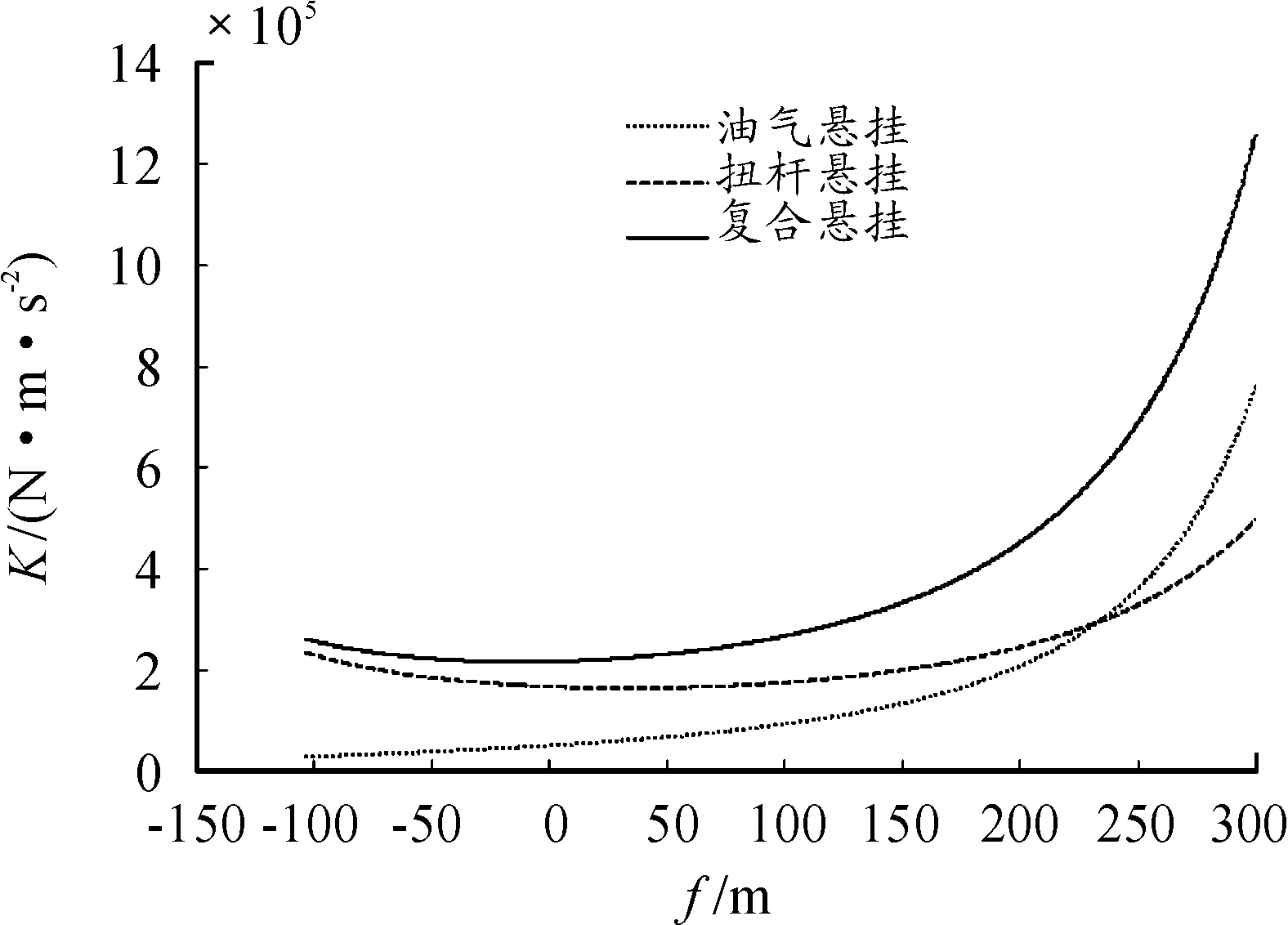
圖4 復合懸掛剛度特性曲線

圖4～圖5中扭桿懸掛彈性力幾乎呈線性增長，其剛度變化不大，而油氣懸掛在小行程時彈性力變化不大，剛度較小，在大行程時呈現較明顯的非線性特性，剛度增長較快，最大行程時的剛度比靜平衡位置的剛度大15倍以上，復合懸掛彈性力符合預期增長趨勢，在小行程時基本呈線性增長，在大行程時迅速增長，具有一定程度的非線性。

1.4 復合懸掛靜載荷分配研究

為獲得理想的目標特性曲線，在H、fd等參數一定的條件下，為方便對比分析，盡可能使fj保持一致，研究復合懸掛中扭桿懸掛和油氣懸掛靜載荷匹配對懸掛性能的影響規律。利用Matlab編程仿真分析，得到λ從0到1，即純油氣懸掛—復合懸掛—純扭桿懸掛變化過程中的彈性元件參數及復合懸掛性能參數變化情況如表2所示。

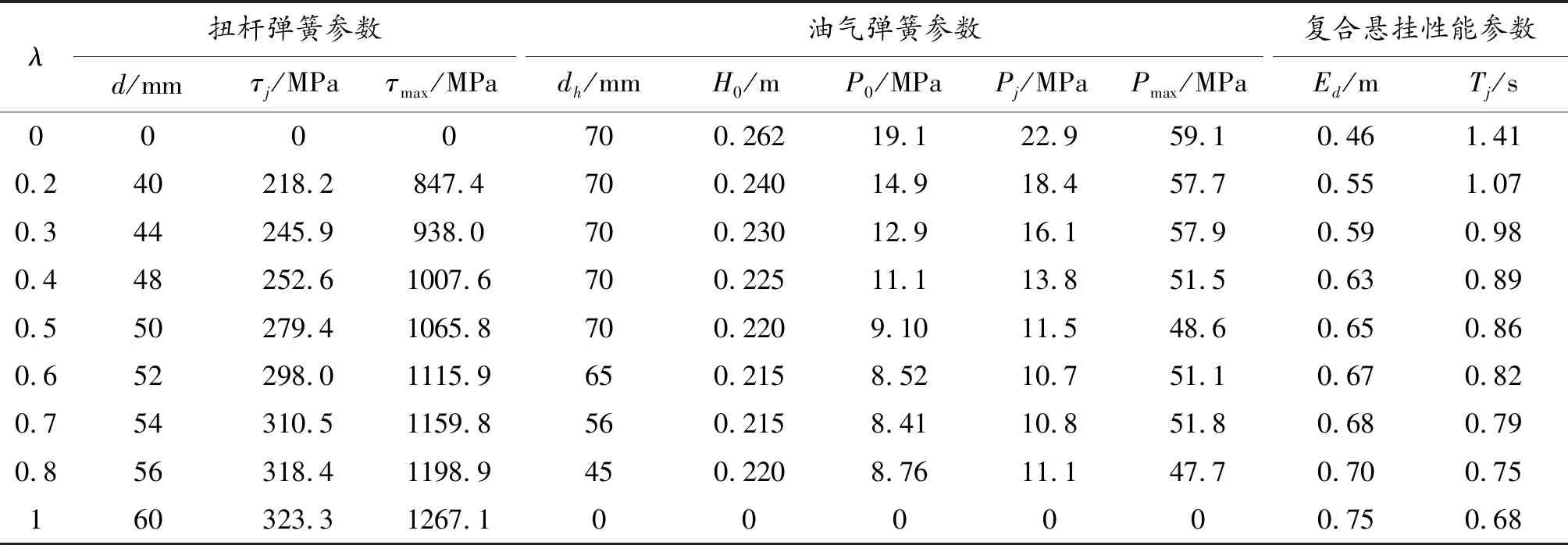
表2 彈性元件參數及復合懸掛性能參數

在每個λ取值時，扭桿直徑d和浮動活塞直徑dh取標準值，dh在λ為0～0.5時為70 mm。這是由于油氣懸掛承受載荷過大，所需要的dh已超過布置空間限制；對于dh和H0的設定應當以使復合懸掛具有一定程度的非線性特性及Pmax不超過壓力閾值為依據。可從表2中看出以下幾點：

1) 復合懸掛使扭桿懸掛、油氣懸掛各自分擔一部分載荷，降低了扭桿彈簧的剪切應力和油氣彈簧的壓強，因而相對于純扭桿懸掛和純油氣懸掛，彈性元件可靠性得到提高，振動周期和動比位能介于純扭桿懸掛和純油氣懸掛之間。因此，扭桿油氣復合懸掛的實質是行駛平順性在純油氣懸掛和純扭桿懸掛之間折中，并使彈性元件可靠性提高。

2)λ增大，d逐漸增大，dh在布置空間限制下逐漸減小，H0逐漸減小。

3) 隨著λ增大，Ed逐漸增大，說明緩沖可靠性提高，Ts減小，說明行駛平順性變差。

4)λ為0～0.3時，油氣懸掛起主要作用，因而此區間復合懸掛靜剛度較小，自由振動周期比較理想，但油氣懸掛承載過大，導致油氣彈簧壓力過大，對密封件要求較高。λ為0.8～1時，扭桿懸掛起主要作用，剛度較大，因而動比位能較大，但扭桿彈簧剪切應力較大，甚至超過許用剪切應力，發生斷裂；通過仿真分析發現復合懸掛特性曲線基本貼合扭桿懸掛特性曲線，油氣懸掛此時所起作用已經很小，復合懸掛非線性較弱，如圖5所示。因此，在不考慮溫升帶來的特性變化的條件下，λ在0.3～0.8，才可能使復合懸掛工程可實現，并達到利用油氣懸掛非線性特性的初衷。

然而當車輛長時間工作或在惡劣工況下行駛時，油氣彈簧溫度升高，氣體膨脹，會導致車姿發生一定程度變化，懸掛特性也會發生一定變化，若車姿變化較大，將會影響車輛的正常行駛。

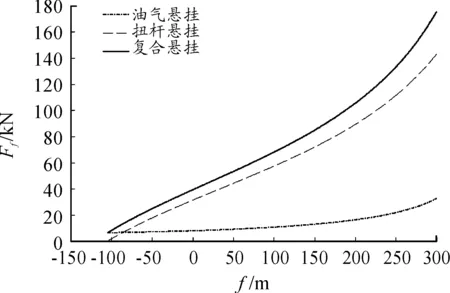
圖5 λ為0.8的彈性特性曲線

2 油氣懸掛的溫升引起車姿變化對復合懸掛性能的影響

油氣懸掛的溫升會導致車姿升高，假設新靜平衡位置溫度為T1，車姿升高量為H1，則溫度變化系數TK為：

TK=T1/Tj

(14)

由式(8)可推出：

Pj1(H0-sj1)=TK(H0-sj)Pj

(15)

式中：sj為車姿升高前的油氣彈簧靜行程；Pj1、sj1分別為車姿升高后的氣體壓強和油氣彈簧靜行程。

車姿升高H1，αj將增大，扭桿懸掛在新靜平衡位置的彈性力Fnt1將減小ΔF，而復合懸掛靜載荷不變，因此車姿升高將引起載荷轉移，扭桿懸掛減小的彈性力ΔF將增加到油氣懸掛上，λ為0.5時的載荷轉移原理圖如圖6。

因此，油氣懸掛在新靜平衡位置的彈性力Fyj1為：

Fyj1=Fyj+ΔF

(16)

車姿升高后，杠桿比變為I1，由式(10)可推出Fyj1和Pj1、I1的關系。且sj與H1存在一定的對應關系，因此可通過迭代法求出H1的值。

利用Matlab編程，得到了不同λ下的車姿變化量隨溫度的變化曲線，如圖7所示。

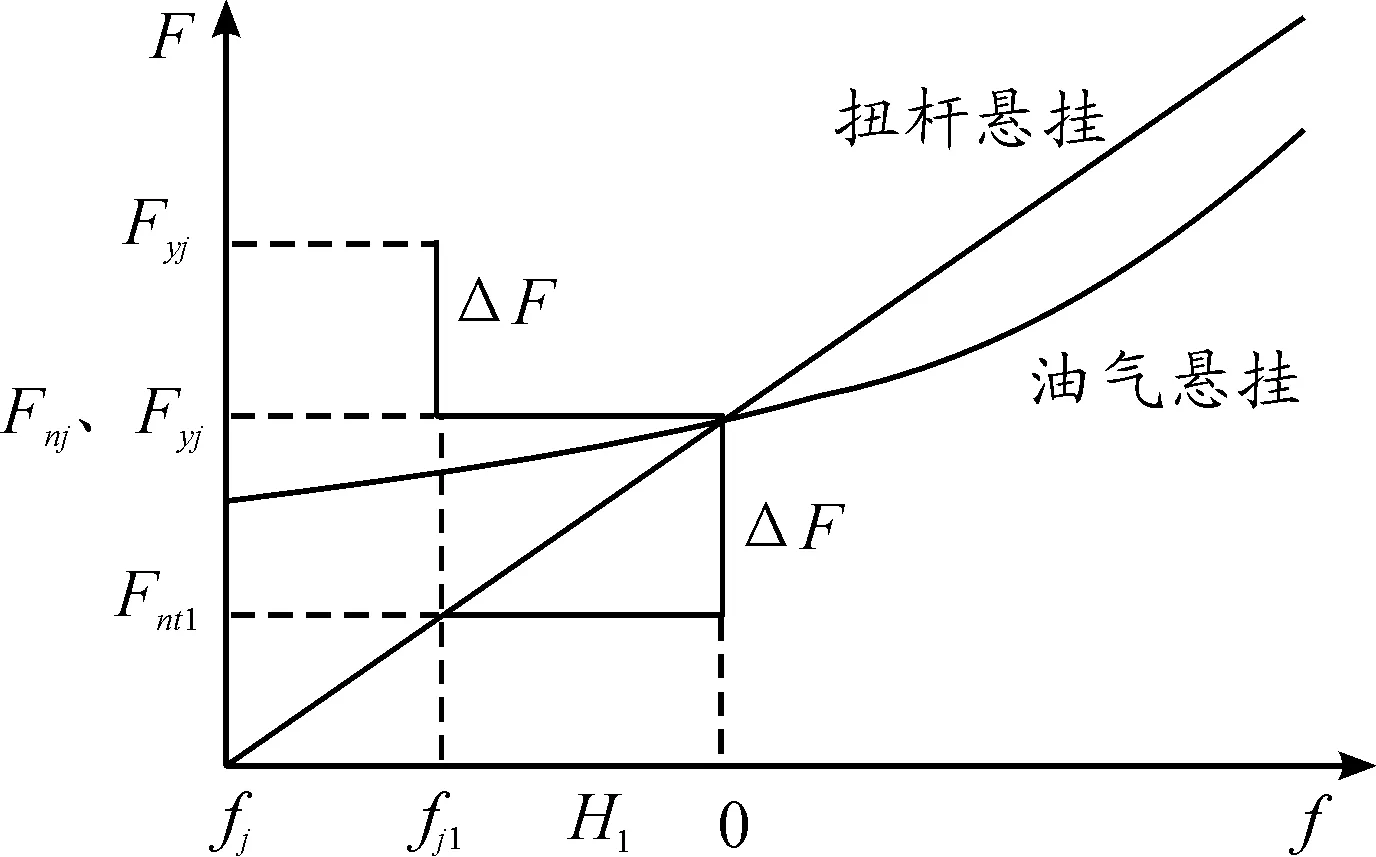
圖6 載荷轉移原理圖

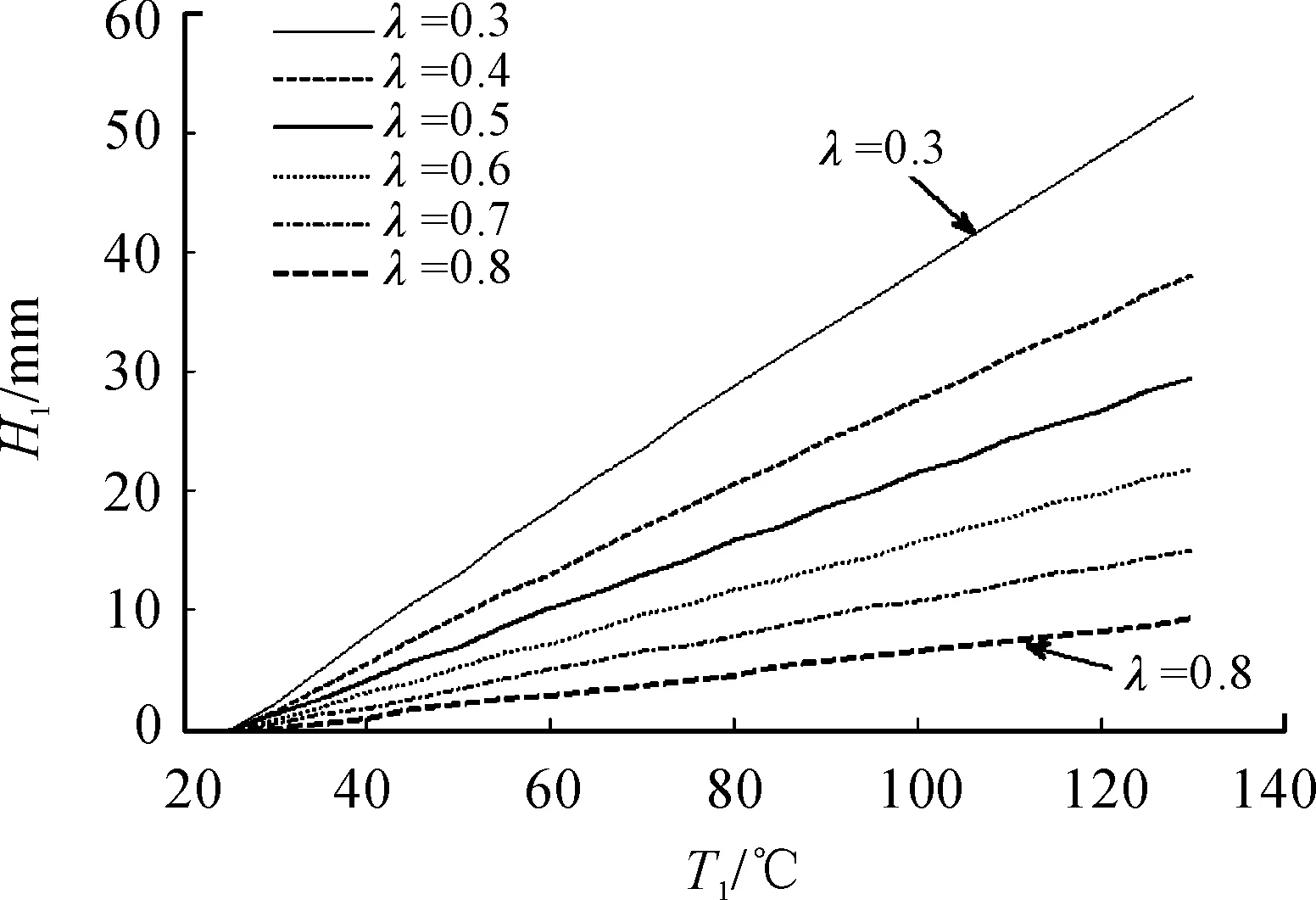
圖7 不同λ下的H1與溫度的關系曲線

從圖7可看出，隨著溫度的升高，H1基本上呈線性增長趨勢，在λ為0.4時，溫度升高至130 ℃，車姿變化量達到了靜行程的38.1%，會影響車輛的行駛狀態。當λ逐漸增大，車姿升高量逐漸減小，且增長趨勢也減緩，當λ為0.8時，溫度升高至130 ℃時，車姿變化量為靜行程的8.9%。由此可見溫升和λ對車姿變化量影響較大。

溫升導致車姿發生變化引起載荷轉移，會使懸掛特性曲線發生改變。λ為0.5時，溫度升高至130 ℃與常溫下的車姿變化前后的懸掛特性曲線對比如圖8所示。

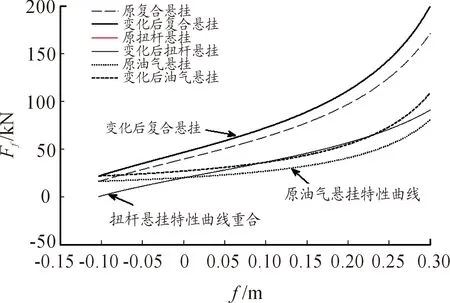
圖8 車姿變化前后懸掛特性曲線對比

由圖6可知，扭桿懸掛在新的靜平衡位置的靜載荷減小，但只是靜平衡位置點發生改變，因此在圖8中扭桿懸掛特性曲線在溫度變化時是重合的。而油氣懸掛靜載荷則相應增加，油氣懸掛的特性曲線將會發生變化，從圖8中可看出，油氣懸掛彈性力整體較車姿變化前增大，因而使得復合懸掛的彈性力整體增大。

根據圖8和式(12)、式(13)可知，復合懸掛動比位能增加，緩沖可靠性得到提高；復合懸掛靜剛度在車姿變化前后基本不發生改變，因此車姿變化對自由振動周期影響不大。

另一方面，油氣彈簧壓強增大才使得油氣懸掛彈性力增大，因此，溫升后的氣體壓強也是考慮的因素之一。經計算，在130 ℃時，Pmax上升到了60 MPa。若油氣懸掛承載較大，則壓強會更高，密封件將受到更大壓力。因此，對于本設計的復合懸掛，在H和fd一定和當前密封件技術水平下，λ應當在0.5～0.8選擇較為合適。

3 結論

1) 扭桿油氣復合懸掛的實質是行駛平順性在純油氣懸掛和扭桿懸掛之間折中，并使彈性元件可靠性提高；

2) 靜載荷分配系數λ對復合懸掛特性參數和彈性元件的可靠性有重要影響；

3) 在現有扭桿材料和油氣彈簧密封技術水平下，λ應當為0.5～0.8，才能實現該復合懸掛工程，且性能有所提高；

4) 采用復合懸掛后，油氣懸掛的溫升引起車姿升高現象較純油氣懸掛有明顯改善，不會對行駛平順性產生影響。