激光超聲信號與缺陷定量檢測機理研究

張思思,鄭 賓,b,郭華玲,b,宋 潮,郭震津

(中北大學 a.電氣與控制工程學院；b.電子測試技術重點實驗室， 太原 030051)

近年來，大量新材料和新設備的安全運行與國家的軍事、工業及經濟發展息息相關[1]。由于材料和設備在使用過程中易出現聚合物，從而產生缺陷，這將造成致命性后果[2-4]。激光超聲無損檢測技術由于具有空間分辨率高，檢測靈敏度好及非接觸性等優良特性，在檢測領域受到越來越廣泛的應用[5-10]。激光超聲無損檢測技術基于材料的結構動力學響應反演缺陷特征，激光激發的超聲信號是激光載荷與被輻照材料之間相互耦合作用的結果。激光超聲在試件中產生的位移信號包含被測材料結構特征、激光脈沖參數特征及超聲波與缺陷相互作用等特征信息，是缺陷定量檢測關鍵的信息來源。

激光超聲無損檢測技術的關鍵是超聲波與缺陷相互作用機理，由超聲信號定量表征缺陷特性是長期以來的技術難題，因此受到了廣泛的關注和研究。關建飛等[11]采用有限元分析法對信號進行特征分析，研究了聲表面波與鋁板缺陷相互作用。敦怡等[12]建立非線性超聲檢測系統研究超聲波與金屬材料中裂紋的相互作用。曾偉[13]基于能量分析的激光超聲技術，對表面帶有網孔缺陷的鋁樣品等進行超聲檢測，分析了距離缺陷不同位置處的超聲信號能量分布情況。V YU ZAOETSEV等[14]主要從應力應變以及能量損耗角度解釋裂紋參數與波形之間的關系。 Hong K M等[15]利用光學方法進行非接觸式缺陷檢測，通過脈沖回波方法對復合材料缺陷進行定量檢測。中北大學秦峰等[16]研究了缺陷深度和超聲波能量衰減值的關系，但理論能量衰減值僅局限于缺陷的深度層面。

本文研究對象是鋁板在激光超聲無損檢測系統中的超聲反射回波信號，首先將超聲信號理論能量衰減值精確到缺陷深度和寬度范圍，提高理論能量衰減值與實際能量比例系數的精度；然后對比例系數與缺陷深度進行多項式擬合，并推出實際能量值與缺陷深度的關系式；最后根據實際能量值反推缺陷的深度值，實現對缺陷的定量評價。

1 能量衰減理論能耗

金屬結構存在裂紋時，系統采集到的超聲信號能量會出現衰減現象[17]。設彈性波的波長為δ，裂紋的深度為d，裂紋的寬度為w，超聲信號低頻理論能耗WLF(d?δ)、高頻理論能耗WHF(d?δ)及最大理論能耗Wcrack為：

WLF≈2πωT(α2K2/k)d5ε2

(1)

(2)

Wcrack≈2πT(α2K2/ρC)d3ε2

(3)

(4)

(5)

(6)

其中：ω為彈性波頻率；Τ為溫度；α為材料的熱膨脹系數；Κ為體模量；ρ為密度；k為熱傳導率；ε為微缺陷的平均應變。在本系統中，T=650，k=238，α=2.3×10-5，K=73.5×109，w=0.15 mm，d=0.1～0.8 mm，δ=c/ω，c=3.0×108，δ=120 m，d=1×10-3m，信號的理論能量衰減值采用超聲低頻理論能耗。

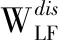
(7)

2 實驗系統與實驗方法

本研究所采用的實驗裝置示意圖如圖1所示，裝置中的Nd:YAG脈沖激光器為納秒級，其波長為1 064 nm，脈沖寬度為7 ns，能量在70～220 mJ連續可調。光學調制模塊采用焦距為75 mm的平凸透鏡，其聚焦極限為20 μm。測量單位中的超聲探頭中心頻率為2.5 MHz，帶寬為5 MHz，探測范圍為0～5 MHz。數據采集模塊使用Tektronix(泰克科技)DPO3034數字熒光示波器。實驗對象為鋁制標準樣件，大小為200 mm×80 mm×10 mm，在邊界80 mm處加工寬度為0.15 mm、深度為0.1～0.8 mm的裂紋。

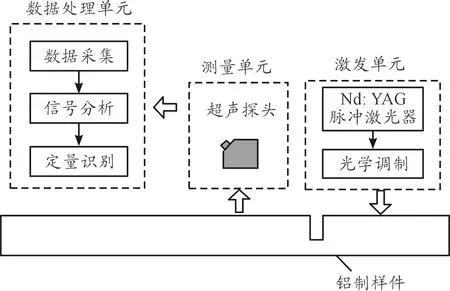
圖1 激光超聲無損檢測系統裝置

Nd:YAG激光器發出激光脈沖，經過光學調制單元進行調制后，照射到鋁制樣件表面，由熱彈機制激發出超聲縱波、橫波和表面波，縱波和橫波沿樣件內部傳播與內部缺陷相互作用產生波形畸變，表面波沿試件表面傳播，與近表面缺陷作用后產生波形畸變；由超聲探頭測量試件表面的畸變波形信號；控制數據采集單元采集測量到的超聲信號，并存儲到計算機中，經信號分析單元提取畸變波形信號中的缺陷特征量；通過數據處理技術，實現樣件近表面微小缺陷的定量化檢測。

其中，實驗采集數據的步長為0.1 mm，采樣頻率為500 MHz，采樣點數為10 000個，針對同一缺陷深度的鋁板實驗，進行3次重復采集。圖2為實驗原理的二維示意圖。

3 結果與分析

首先，系統對鋁板樣件進行激光超聲激勵，對采集系統輸出的反射回波信號預處理；其次，分別計算信號的理論能量衰減值在精度提高前后與實際能量的比例系數，對比例系數與缺陷深度進行多項式擬合；再次，通過擬合參數選出最佳擬合公式，推導出實際能量值與缺陷深度的關系式；最后，根據實際能量值反推出缺陷深度，實現對缺陷的定量評價。

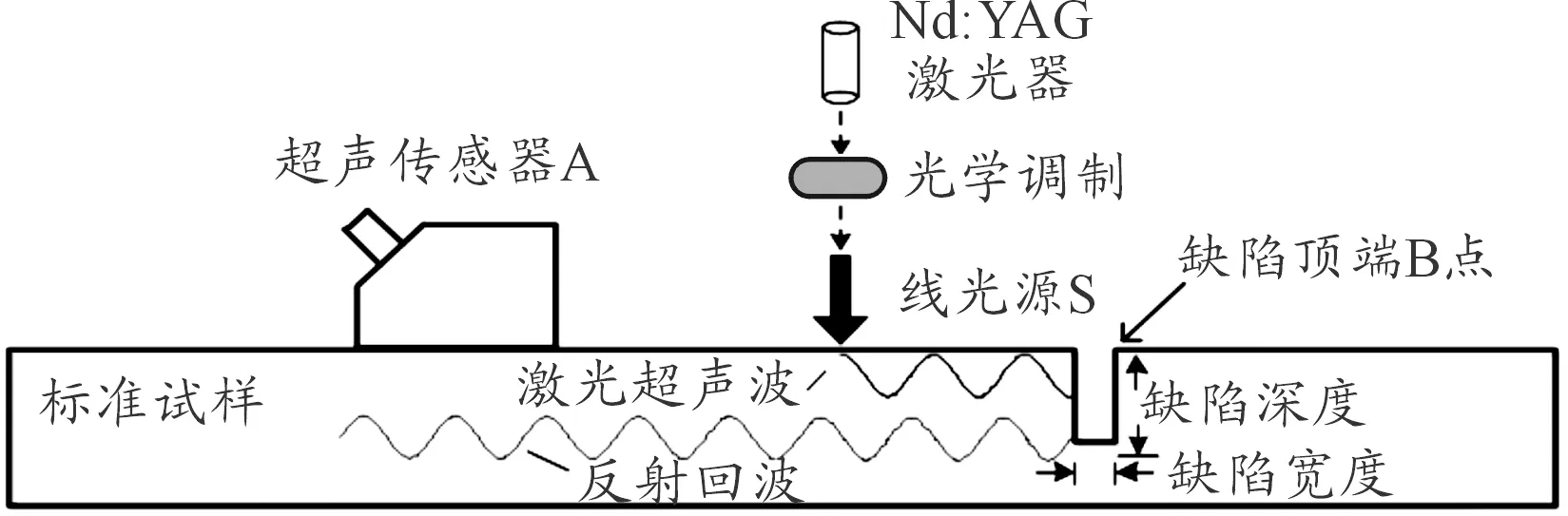
圖2 實驗原理二維示意圖

3.1 實驗預處理

為了突出缺陷特征對超聲回波信號的影響，避免其他因素影響，每次實驗重復3次。通過算術平均算法對缺陷深度為0.1～0.8 mm反射回波信號進行預處理提高信號的信噪比。圖3為缺陷深度為0.1 mm的超聲信號通過預處理后的時域[圖3 (a)]和頻域[圖3 (b)]波形，橢圓中的信號為反射回波信號。

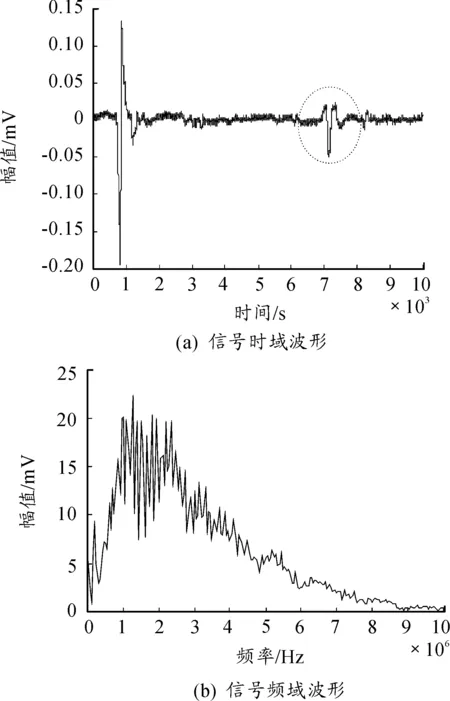
圖3 缺陷深度為0.1 mm的超聲波形

3.2 實驗數據分析

3.2.1 信號能量的比例系數

金屬缺陷超聲信號的能量是表征缺陷特征的參量。缺陷的寬度一定，深度不同時對應頻域的能量分布也不同。反射回波信號頻域的能量分布包含缺陷參量，文中缺陷實際能量值為信號頻域幅值的平方和，即對反射回波信號進行傅里葉變換，最后將頻率對應的幅值進行平方和；理論能量衰減值可根據式(7)近似得到。理論能量衰減值Et與實際能量值E0的比值為比例系數kr如表1所示，根據表1的數據可以作出圖4。

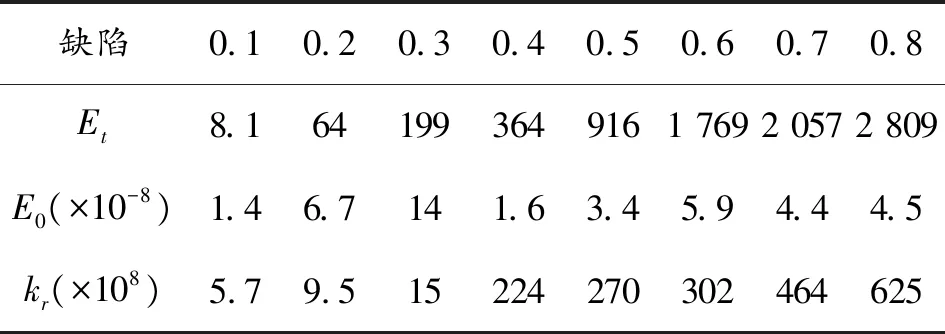
表1 缺陷的理論、實際能量值和比例系數值

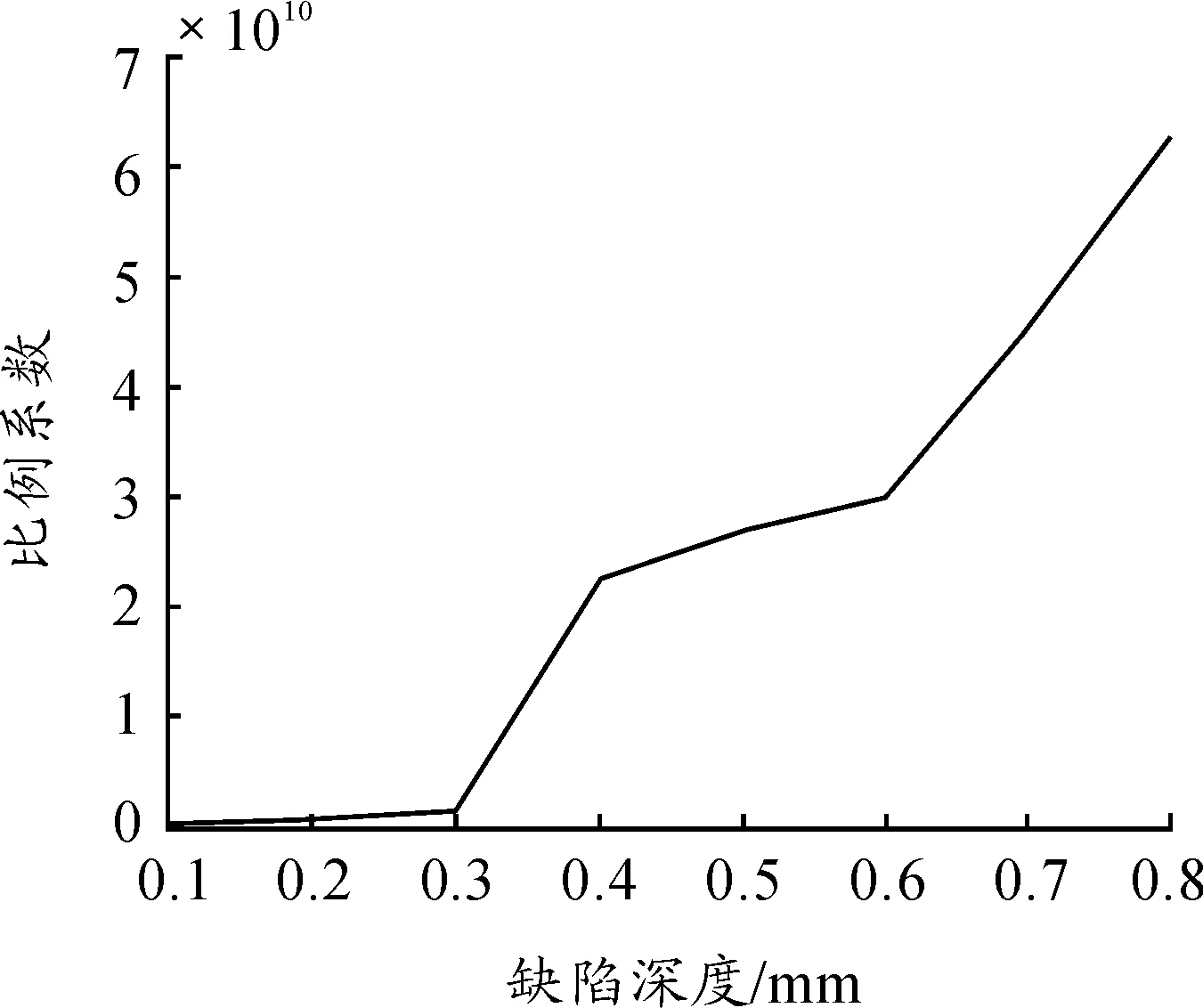
圖4 缺陷深度與比例系數關系

由圖4可知，隨著缺陷深度的增大理論能量衰減值增大，比例系數隨缺陷深度的增大而增大。

3.2.2 信號比例系數和缺陷深度的擬合

使用線性、多項式及冪函數對缺陷深度與比例系數擬合如圖5所示。

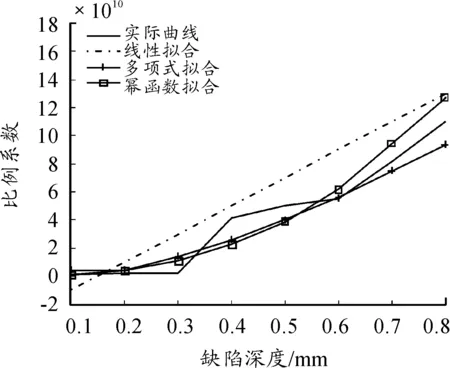
圖5 比例系數與缺陷深度關系擬合函數

擬合評價參數SSE(和方差)、MSE(均方差)、RMSE(均方根)參量值如表2所示。

由表2可知，多項式擬合的各評價參數值最小。從圖5可知，多項式擬合曲線最接近實際比例系數。

表2 擬合函數的評價參數

注：SSE：和方差；MSE：均方差；RMSE：均方根

不同次數多項式擬合的比例系數與理論值的相對誤差如表3所示。不同次數多項式擬合的比例系數與理論值關系如圖6所示。

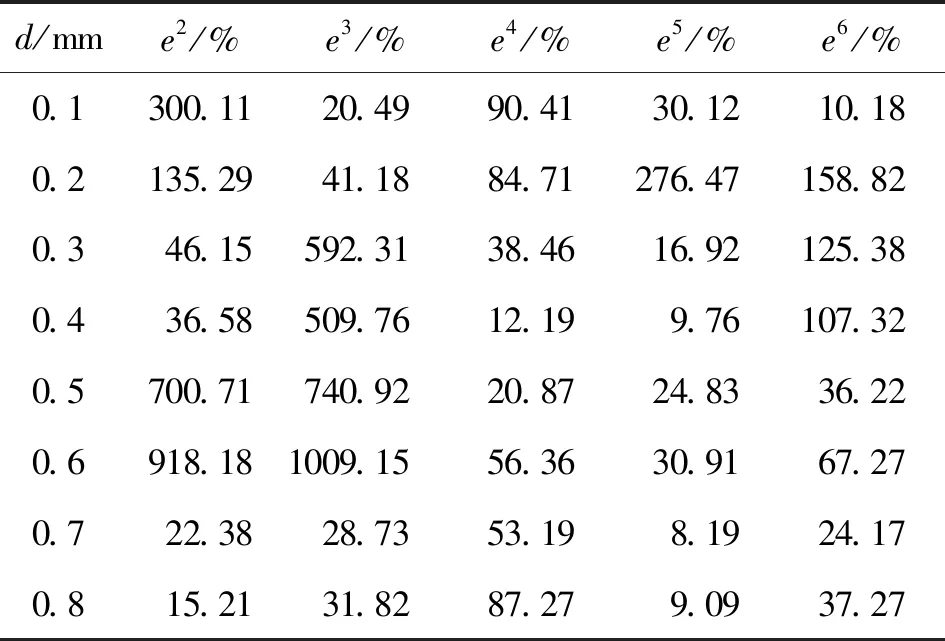
表3 不同次數多項式擬合比例系數與理論值的相對誤差

注：e2～e6指：二次～六次多項式擬合比例系數相對誤差

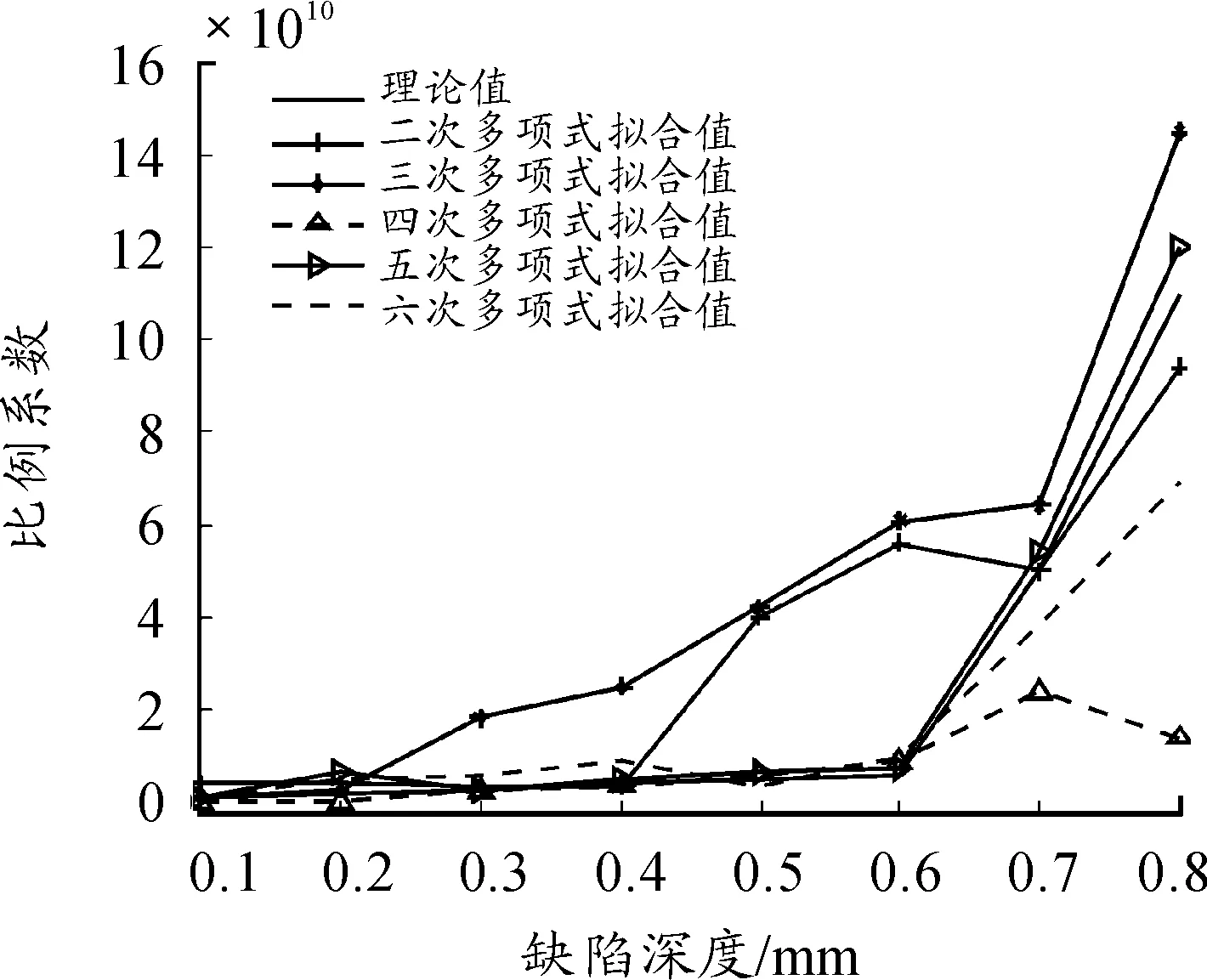
圖6 不同次數多項式擬合的比例系數與理論值關系

根據表3可知，五次多項式的擬合比例系數相對實際比例系數的相對誤差最小；由圖6可知，五次多項式擬合出的比例系數最接近理論比例系數值。本系統中的比例系數kr與缺陷深度L的擬合公式采用五次多項式：

kr=-5×1027d5-1×1025d4-1×1022×d3+

5×1018d2-9×1014d+7×1010

(8)

比例系數、理論能量衰減值和實際能量值分別為：

kr=Et/E0

(9)

Et=∑(2πωT(α2K2/k)d3w2)

(10)

E0=∑H(ω)2

(11)

其中，H(ω)為缺陷回波信號頻域的幅值大小。

聯立式(8)和式(9)，根據缺陷實際能量值求出缺陷深度(見表4)。其中，d1和d2分別為理論能量衰減值精度提高前后反推的缺陷深度值。

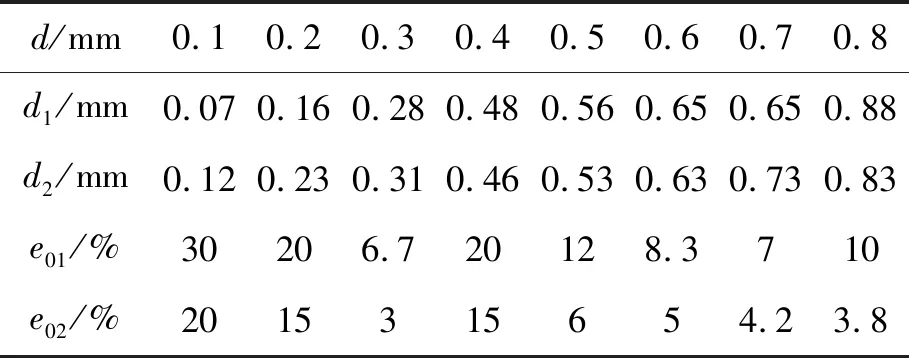
表4 理論缺陷深度與實際缺陷深度

注：d:實際缺陷深度；d1、d2:理論能量衰減值精度提高前、后理論缺陷深度；e01、e02理論能量衰減值精度提高前、后理論缺陷深度與實際缺陷深度的百分誤差。

由表4可知，當理論能量衰減值精確到寬度和深度范圍時，反推出的缺陷深度值更精確且百分誤差較小；理論缺陷深度與實際缺陷深度百分誤差在3%～20%范圍，說明利用信號實際能量值反推缺陷深度具有一定可行性。

4 結論

通過數字平均算法對信號進行預處理，將缺陷的理論能量衰減值精確到深度和寬度范圍，得到理論能量衰減值與實際能量的比例系數；并對比例系數與缺陷深度進行多項式擬合，得到實際能量值與缺陷深度的關系式；最后利用信號的實際能量值求出缺陷深度。實驗結果表明，將缺陷的理論能量衰減值精確到缺陷的深度與寬度范圍，提高了缺陷深度檢測的精度值。