開孔率對明基床上開孔沉箱規則波反射系數影響的數值研究
蔡 郁,孫大鵬,趙沛泓,吳 浩
(1.中交水運規劃設計院有限公司,北京 100007;2.大連理工大學 海岸和近海工程國家重點實驗室,大連 116024)
開孔沉箱結構可以使傳播到開孔沉箱前的波浪產生一定的相位差,降低波浪能量,避免波浪沖擊力的相互疊加,減小波浪反射及結構受力,減輕對結構的破壞,相比直墻式沉箱結構,在港口工程實際建設中具有明顯的優勢。近年來,開孔沉箱已逐漸成為學者們的主要研究課題,張芹[1]、戴冠英[2]開展了波浪與開孔直立結構相互作用的物理模型試驗,得出當μ為0.18~0.25時,開孔直立墻具有十分顯著的消浪效果;陳雪峰、李玉成[3]等借助物理模型試驗總結了開孔沉箱前波浪反射系數與相對消浪室寬度、開孔率、波陡等影響因素之間的關系;郭科、曲淑媛[4]等實測現場堤前反射系數,對直墻式沉箱與開孔沉箱的消浪效果進行了研究;行天強、孫大鵬[5]在物理模型試驗中,考慮相對基床高度,總結了開孔沉箱前波浪反射系數與各影響因素之間的關系,并擬合了相應的計算關系式。現有的物理模型試驗成果中,開孔率μ的通常取值范圍為0.2~0.4,且以線性關系來描述μ與Kr之間的關系。然而,對于μ<0.2或μ>0.4時,μ與Kr的關系卻尚未得知。
針對這一問題,本文借助數值方法,建立波浪水槽,開展了規則波與可滲明基床上開孔沉箱相互作用的模型試驗,在擴大的開孔率取值范圍內(μ=0.1、0.2、0.3、0.4、0.5,其中μ=0.2、0.4為物模試驗[5]工況),探求μ與Kr之間的關系。研究成果對港口工程實際建設具有參考價值。
1 數值波浪水槽的建立
1.1 數值方法
本文數值方法的控制方程為體積平均-雷諾平均N-S方程[6]
(1)
(2)
式中:〈〉表示固有體積平均物理量;〈〉f表示表觀體積平均物理量;n為多孔介質孔隙率;cm=0.34(1-n)/n為附加質量系數;ρ為密度;P為壓強。
利用相同的方法對k-ε平衡方程和動量方程進行體積平均
(3)
(4)
借助日本科學家Nakayama和Kuwahara (1999)[7]的研究成果,對ε∞和k∞進行封閉后,得到
(5)
(6)
式中:σk=1.00;σε=1.30;Cε1=1.44;Cε2=1.92為湍流模型中的常數;vt為體積平均的附加湍動能粘性系數;k為湍流動能;ε為特征量。
借助CLEAR-VOF方法追蹤自由水面,并采用三步有限元方法對上述方程進行數值離散求解。
1.2 造波穩定性驗證
本文建立的數值水槽中,造波端采用主動吸收式造波[8-9]方法 ,防止造成干擾試驗結果的二次反射波出現,在數值水槽中放入浪高儀記錄實時波高情況,借助濾波變換的方法將浪高儀器采集的數據進行分離,造波端接到分離出的修正信號后,只保留入射波,實現目的。
現將數值水槽右邊界定義為直墻,驗證主動吸收式造波的性能,計算域長度為7.7 m,水深為0.4 m,如圖1所示。
采用入射波高為H=0.06 m,周期T=1.4 s的規則波進行無反射造波驗證試驗。在x=6.5 m和x=7.3 m處布置兩個浪高儀,實時監測波面變化,圖2和圖3為波面隨時間的變化過程。


圖2 x=6.5 m處波高歷時曲線Fig.2 Numerical flume time series of wave elevation at x=6.5 m圖3 x=7.3 m處波高歷時曲線Fig.3 Numerical flume time series of wave elevation at x=7.3 m
從圖2和圖3可以看出,波腹(x=6.5 m處)波高大約為入射波高的兩倍,波節(x=7.3 m處)波高趨近于零,符合波浪的傳播變形特征。說明此數值水槽可以有效消除二次反射波的影響。
2 數值計算結果分析
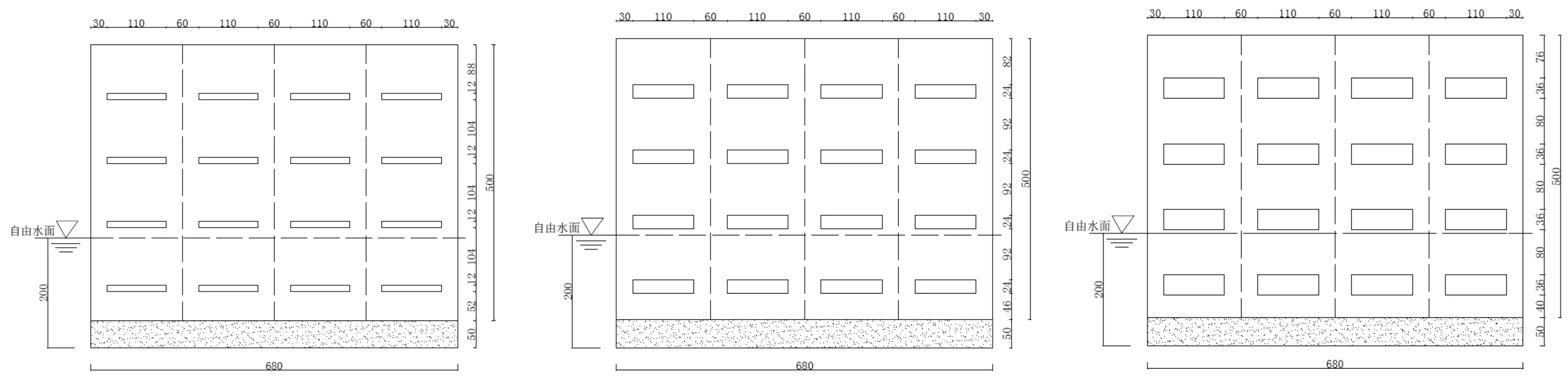
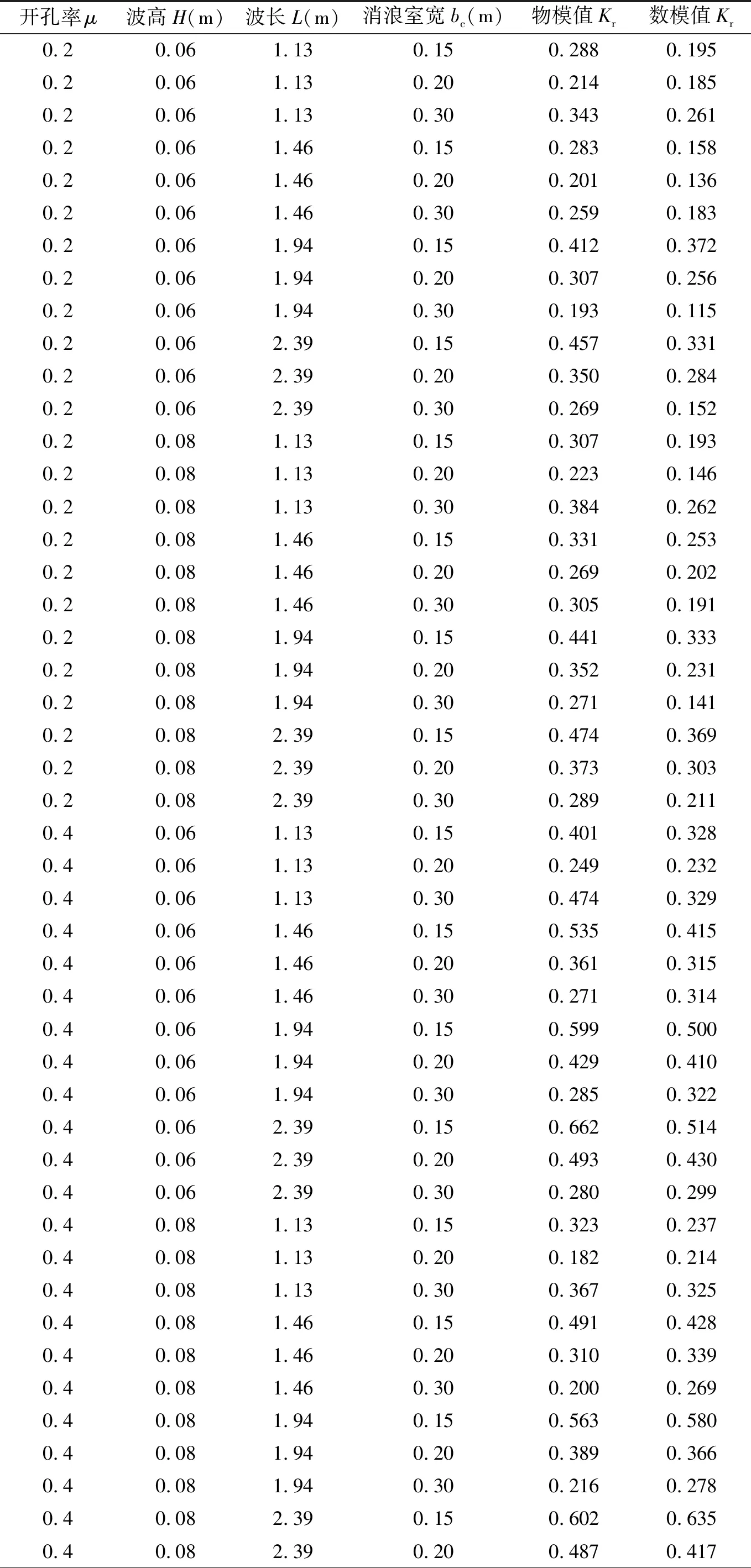
圖4為數值波浪水槽布置示意圖,數值水槽最左端為造波板,最右端設置可滲明基床及開孔沉箱結構模型,基床前水深d=0.4 m,基床高度hm=0.15 m。開孔沉箱前墻部分為開孔板,后墻部分為實體墻,消浪室內0.15 m 圖4 數值波浪水槽布置示意圖Fig.4 Sketch of the numerical flume 波要素取值范圍波高H0.06 m,0.08 m周期T0.86 s, 1.0 s, 1.2 s, 1.4 s波長L1.13 m,1.46 m,1.94 m,2.39 m開孔率μ0.1,0.2,0.3,0.4,0.5消浪室寬度bc0.15 m,0.20 m,0.30 m 不同開孔率下的開孔板細部尺寸如圖5所示,單位為mm。 5-a μ=0.1開孔位置示意圖5-b μ=0.2開孔位置示意圖5-c μ=0.3開孔位置示意圖 5-d μ=0.4開孔位置示意圖5-e μ=0.5開孔位置示意圖圖5 開孔板位置示意圖Fig.5 The shape of perforated caisson orifice 為驗證數值波浪水槽的可靠性及準確性,本文首先模擬了與物模試驗[5]相同的試驗工況(μ=0.2、0.4),并將二者計算結果進行對比,見表2。 要理順關系。一年來我們感到,各種關系理順了,工作會事半功倍。要依靠集團紀委的正確領導、職能部門的有力指導,要積極利用地方紀委監委專業資源和力量,更要得到監督單位的充分理解配合,派駐優勢才能得到最大發揮。 表2 本文數模值與物模值對比(hm=0.15 m,d=0.4 m)Tab.2 Comparison of Kr between norm value and physical experiment value in front of caisson 0.40.082.390.300.2400.264 從表中可以看出,當開孔率μ=0.2時,反射系數的數模值略小于物模試驗值;當開孔率μ=0.4時,數模值與物模試驗值吻合良好,表明本文建立的數值水槽具有較高的計算精度,可以用來計算新的試驗工況。 物模試驗[5]研究成果中關于規則波作用下可滲明基床上開孔沉箱前的波浪反射系數與各影響因素之間的計算關系式如下 圖6 數模值Kr與公式計算值Kr的比較Fig.6 Comparisons between the numerical modulus Krand the formula Kr (7) 式中:Kr為開孔沉箱前的波浪反射系數;L為波長;hm為基床高度;bc為消浪室寬度;d為基床前水深;μ為開孔率。 公式(7)的μ的取值范圍為0.2≤μ≤0.4,且Kr和μ呈線性關系。 利用本文數值波浪水槽模擬開孔率μ=0.1、0.3、0.5的試驗工況,本文數模計算值與公式(7)計算值的對比結果見圖6所示。 從圖6可以看出,當開孔率μ=0.2、0.3、0.4、0.5時,開孔沉箱前波浪反射系數均分布在y=x兩側,并落在y=x±0.1的包絡線范圍內;而當開孔率μ=0.1時,數模值整體上大于公式(7)的反射系數計算值。 7-a L=1.13 m, bc=0.15 m7-b L=1.46 m, bc=0.15 m7-c L=1.94 m, bc=0.15 m7-d L=2.39 m, bc=0.15 m 7-e L=1.13 m, bc=0.20 m7-f L=1.46 m, bc=0.20 m7-g L=1.94 m, bc=0.20 m7-h L=2.39 m, bc=0.20 m 7-i L=1.13 m, bc=0.30 m7-j L=1.46 m, bc=0.30 m7-k L=1.94 m, bc=0.30 m7-l L=2.39 m, bc=0.30 m圖7 開孔率μ與Kr之間的關系圖(H=0.06 m)Fig.7 Relational graph of μ versus Kr(H=0.06 m) 以上各圖表明,當μ小于0.2時,隨著μ的逐漸增大,數模值Kr逐漸減小,這是因為當μ足夠小時,即沉箱前壁透水性極小,波浪反射效應明顯增大,符合物理本質,說明Kr與μ的關系不能繼續用物模試驗給出的計算關系式(公式7)來描述;當μ在0.2至0.4之間時,數模值Kr與物模值Kr對比良好,滿足物模試驗擬合的經驗關系式(公式7)的趨勢;當μ大于0.4時,隨著μ的逐漸增大,數模值Kr逐漸增大,這是因為當μ足夠大時,沉箱前壁形同虛設,消浪室后墻成為主要的波浪反射帶,使Kr增大,滿足物模試驗擬合的經驗關系式的趨勢。 研究結果表明當μ在0.1與0.2之間時,μ與Kr是一條存在拐點的曲線,用公式(7)的線性關系來描述二者之間的關系是不恰當的。 本文基于數值模型方法,建立二維波浪水槽,擴大開孔率μ的取值范圍,開展了規則波與可滲明基床上開孔沉箱相互作用的模型試驗,研究Kr與μ的關系,結論如下[9]: (1)當μ小于0.2時, 隨著μ逐漸增大,數模值Kr逐漸減小,不滿足物模試驗擬合經驗關系式的趨勢; (2)當μ在0.2至0.4之間時,數模值Kr與物模值Kr對比良好,滿足物模試驗擬合的經驗關系式的趨勢; (3)當μ大于0.4時,隨著μ逐漸增大,數模值Kr逐漸增大,滿足物模試驗擬合經驗關系式的趨勢。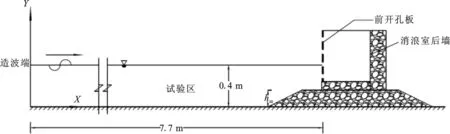

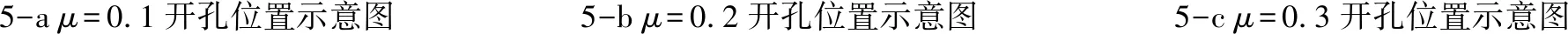


2.1 數值模型準確性驗證

2.2 開孔率對反射系數的影響







3 結論

