氣動引力輔助的火星自由返回軌道設計方法

夏時宇，徐 波

(南京大學天文與空間科學學院，南京 210023)

0 引 言

迄今為止，人類已經成功進行了對太陽系內所有行星的無人探測和對月球的登陸探測。對載人火星探測任務的研究也逐漸升溫，其中關于軌道設計的研究對于任務的成功實施具有十分重要的意義。

載人探測任務的復雜性和危險性都遠遠高于無人任務，對保障航天員安全返回地球提出了更高的要求。為此研究人員提出了自由返回軌道(Free return trajectory)的概念[1]。自由返回軌道是指航天器不需要自身提供變軌能量(或僅提供很少的變軌能量)，通過其他天體的借力飛行，就可以無動力返回地球，因此適合作為載人探測任務故障模式下的中止軌道。自由返回軌道可以作為航天器的初始轉移軌道，如果任務正常進行，則僅需要對軌道進行少量修正即可在目標天體正常入軌，如果發生系統故障，則能夠保證航天員安全返回地球。

自由返回軌道最早應用于對月球的探測，如蘇聯的月球3號任務和美國的阿波羅8、10、11號任務。Berry[1]對阿波羅11號任務中的自由返回軌道、發射窗口以及約束條件等問題進行了研究。黃文德等[2]基于雙二體假設給出了月球自由返回軌道的設計方法，并對軌道傾角、拼接點分布等參數進行了特性分析。文獻[3-4]基于圓錐曲線拼接提出了一種兩段式月球自由返回軌道設計方法，具有精度高、收斂快的特點。自由返回軌道也被推廣到火星探測任務的研究中。Patel等[5]在飛行時間約束和發射能量約束條件下研究了火星自由返回軌道，發現了總飛行時間分別為1.5年、2年和3年的三類自由返回軌道。李楨[6]針對載人火星探測任務，對比研究了地球-火星-地球，地球-火星-金星-地球，地球-金星-火星-地球三類自由返回軌道，并提出使用Tisserand準則進行軌道參數的初步設計。

火星自由返回軌道通常需要使用引力輔助(Gravity assist，GA)。但引力輔助技術受到借力天體的力學性質以及軌道近拱點高度約束，使得航天器雙曲線剩余速度v∞偏轉角度較小，加速效果有限，轉移飛行時間通常較長，不利于航天器在出現故障時快速返回地球。

為解決偏轉角度較小的問題，美國噴氣推進實驗室于1982年提出氣動引力輔助(Aerogravity assist，AGA)變軌技術[7]，如圖1所示，v∞-為初始雙曲剩余速度， Δθ為大氣飛行段轉角，v∞+為經過AGA后的雙曲剩余速度，φ為速度矢量偏轉角。火星由于質量較小，其引力輔助能力也因此較弱[8]，使用AGA可以極大地增加速度偏轉角，獲得更好的加速效果，進而減少所需的借力飛行次數與飛行時間[9]。

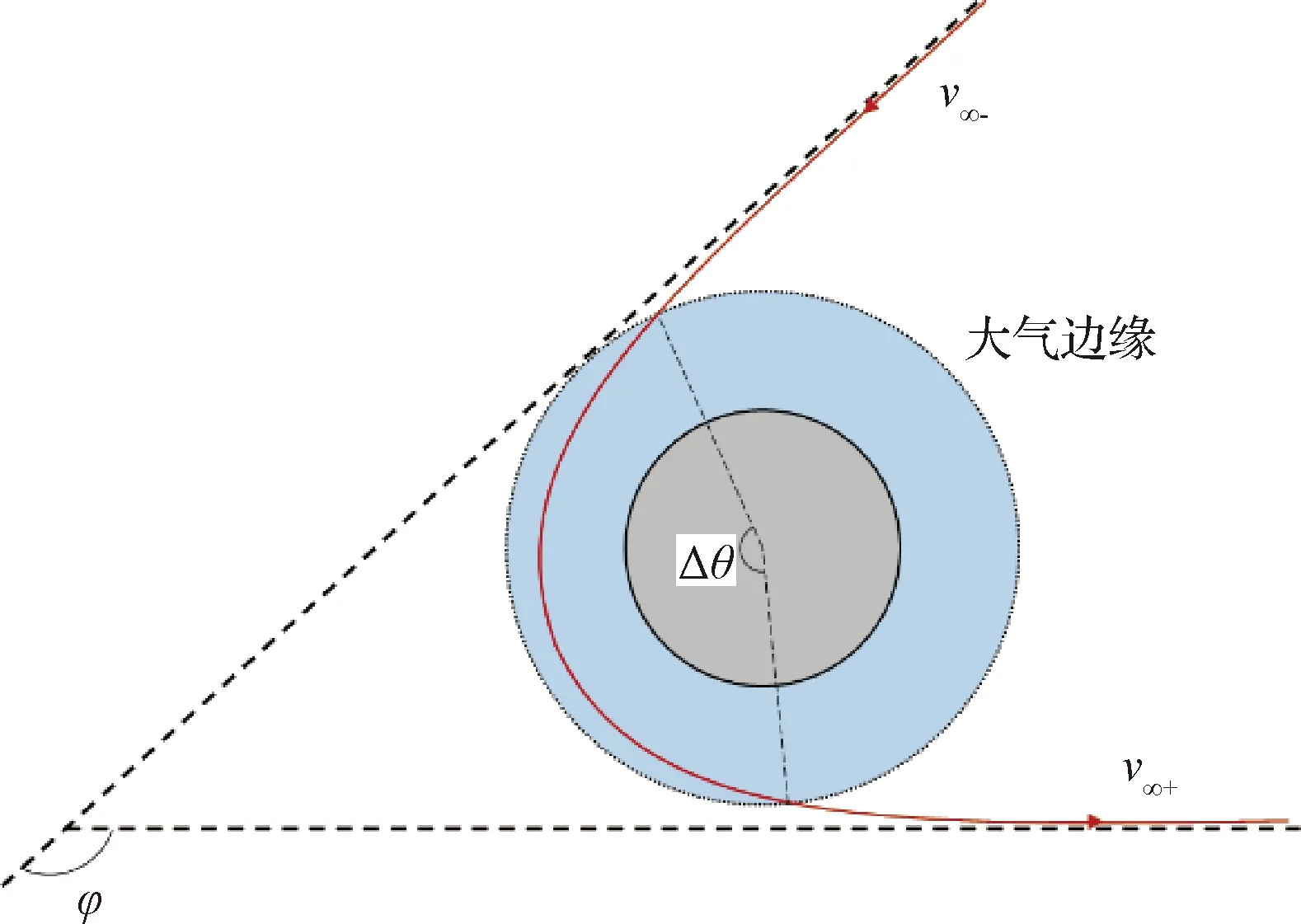
圖1 氣動引力輔助示意圖

氣動引力輔助技術由于其可能帶來的巨大收益得到了大量研究。文獻[10-11]對大氣飛行段進行軌跡優化，在熱負載約束條件下實現最大化飛出速度。文獻[12-13]設計了基于預測校正的制導算法，可以有效克服入軌誤差、大氣密度誤差所帶來的不利影響，保證氣動引力輔助的可靠性和準確性。Mazzaracchio[14]設計了一種基于飛行路徑角的制導算法，并指出熱負載是氣動引力輔助的最主要約束條件。Jesick[15]提出了一種在火星進行兩次AGA的自由返回軌道，具有較小的雙曲剩余速度。喬棟等[16]以探測小行星Ivar為例，提出一種將繪制等高線圖和圓錐曲線拼接相結合的AGA轉移軌道設計方法，該文獻采用了文獻[17]中提出的簡化大氣飛行段模型。

現有利用氣動引力輔助技術的軌道設計研究中，通常將大氣飛行段簡化為水平飛行[9, 15-17]，而忽略了下降和上升過程，與真實的飛行過程不符。為解決這一問題，本文提出一種三段式氣動引力輔助模型，將大氣飛行段分為下降段、平飛段和上升段，使用大氣飛行角和航跡角描述飛行過程，并建立了相應的計算模型。

本文第1節給出了自由返回軌道相關的計算模型，其中包括引力輔助模型，氣動引力輔助模型和軌道優化模型。第2節分別對“地球-火星-地球”、“地球-火星-金星-地球”和“地球-金星-火星-地球”三種序列進行了軌道優化，對比了本文提出的三段式模型和現有文獻中的簡化模型給出的優化結果，并分析了氣動引力輔助對自由返回軌道性能的影響。第3節對全文進行了總結。

1 計算模型

1.1 引力輔助模型

自由返回軌道通常采用圓錐曲線拼接方式構造。航天器在行星間轉移軌道段僅考慮太陽引力，航天器相對太陽做二體運動。在借力飛行段僅考慮借力天體引力，并計算引力輔助引起的相對速度偏轉角φ以及慣性系下的飛出速度V∞+，引力輔助速度矢量關系如圖2所示。其中，Vp,V∞-,V∞+分別為在慣性系下借力天體以及航天器借力飛行前后的速度，v∞-,v∞+為航天器借力飛行前后的雙曲線剩余速度。速度偏轉角φ可用下式計算，

(1)

式中：r0為軌道近心距，μ為借力天體引力常數。引力輔助過程中沒有能量消耗，因此v∞-與v∞+相等。由于r0不能小于借力天體的半徑，速度偏轉角φ是有上限的。

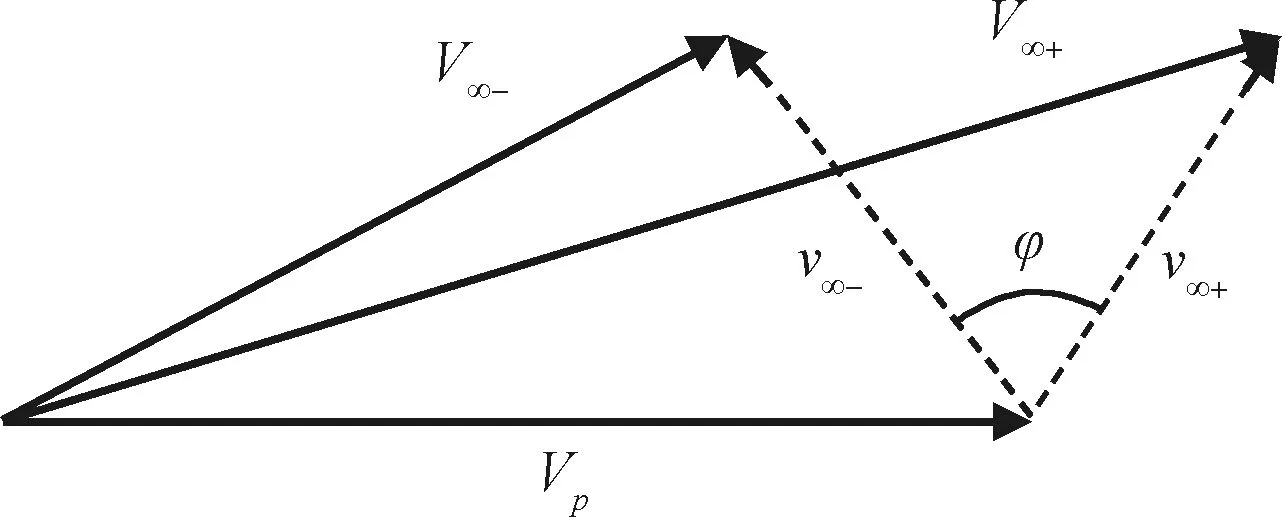
圖2 引力輔助速度矢量關系

1.2 氣動引力輔助模型

氣動引力輔助的速度矢量關系與引力輔助類似，主要區別在于大氣飛行過程會導致一部分速度損失ΔVaero，如圖3所示。本節介紹三段式氣動引力輔助模型以及速度偏轉角φ和雙曲剩余速度v∞+的計算。

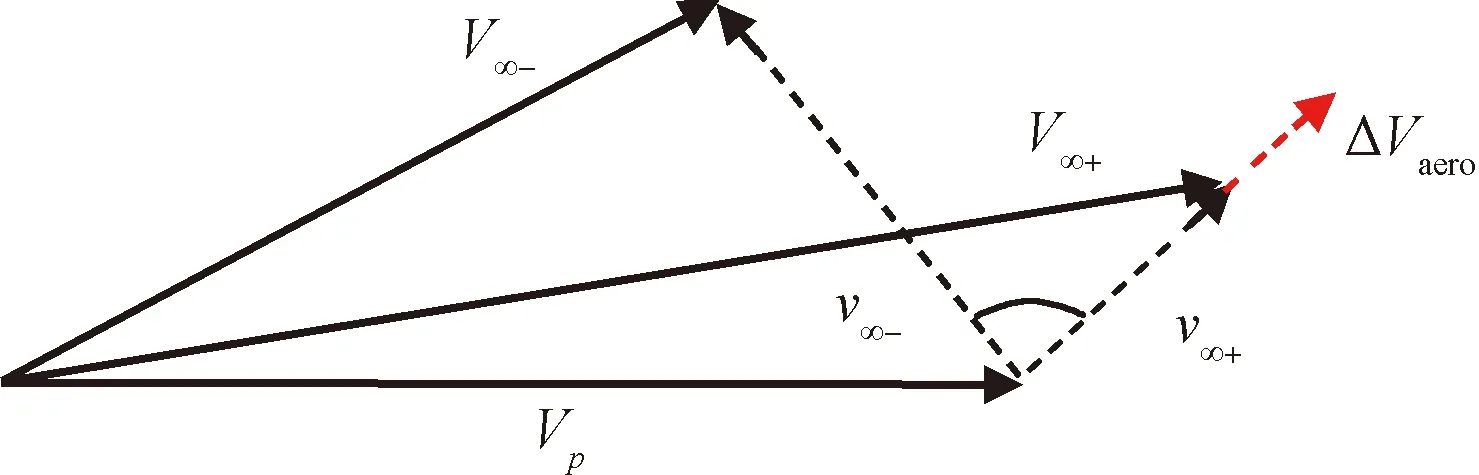
圖3 氣動引力輔助速度矢量關系

本文提出將大氣飛行段劃分為下降段、平飛段和上升段，如圖4所示。其中h,θ,v,γ分別為高度、大氣飛行角、速度和航跡角，Δθ為航天器在各段飛過的角度。在下降段，航天器以初始狀態h0,θ0,v0,γ0進入大氣層并逐漸下降，經過Δθd后到達平飛高度。在平飛段，航天器保持水平飛行狀態飛過Δθe。在上升段，航天器高度逐漸增大，經過Δθa后以末狀態hf,θf,vf,γf飛出大氣層。下面分別對這三個階段進行計算。

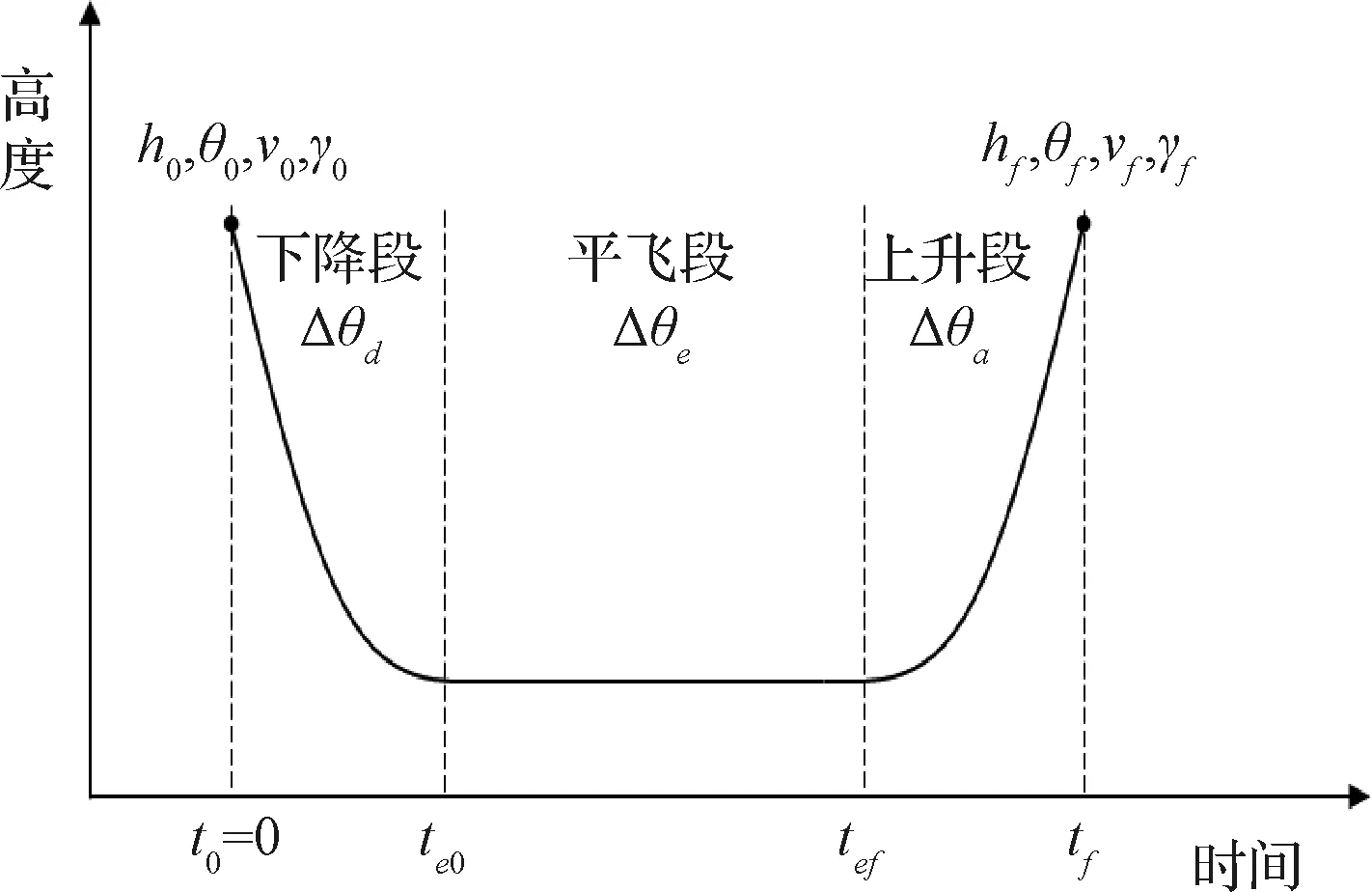
圖4 下降段、平飛段和上升段

1)下降段

由于下降段過程主要發生在大氣密度較低的高層大氣，因此可以近似認為下降段速度大小保持不變，即

v≡v0

(2)

同時根據多個文獻中對氣動引力輔助的仿真結果[12-14],下降段航跡角為小量且隨時間近似線性變化,即

γ=at+γ0

(3)

式中:a為待求系數。

因此可以得到下降段運動方程，

(4)

(5)

式(5)中由于火星大氣層高度遠小于火星半徑，因此可認為r≈r0。

積分式(4)得

(6)

式中:te 0為下降段結束時間，he 0為下降段結束時高度。

將γ(te 0)=0代入式(3)得，

ate 0+γ0=0

(7)

結合式(6)和式(7)可求得

(8)

將式(5)自變量換為γ得，

(9)

積分得到，

(10)

因此下降段航天器飛過的角度Δθd可由式(10)計算得到，其中h0,r0,γ0由初始狀態確定，he 0可采用以下方式計算。

當航天器進入平飛狀態時，由豎直方向受力平衡得，

(11)

式中:L,β,λ分別為升力加速度，航天器彈道系數和升阻比。

大氣密度隨高度指數分布，即

(12)

式中:ρ0,hs分別為參考大氣密度和密度標高。

將式(11)代入式(12)得到進入平飛狀態時的高度，

(13)

2)平飛段

航天器速度的減小主要發生在平飛段，其速度減小可通過文獻[9]中模型計算，計算方式如下，

(14)

式中:D為阻力加速度，將式(14)代入式(5)并取γ=0，得到速度隨大氣飛行角的變化，

(15)

將式(11)代入式(15)，得

(16)

由于航天器處在平飛狀態，gr為常數，可近似取火星表面處數值。積分式(16)可得平飛段末速度與飛過的角度Δθe之間的關系，

(17)

相應的雙曲線剩余速度關系為

(18)

3)上升段

上升段的計算與下降段類似，可以看作下降段的逆過程，即

(19)

式中:hf=h0,rf=r0，飛出大氣層時的航跡角可近似為γf=-γ0，vf可通過式(17)計算。

4)速度矢量偏轉計算

氣動引力輔助過程中雙曲剩余速度矢量大小的減小可以通過式(18)計算得到。而速度矢量的偏轉角關系如圖5所示，其中δ-,δ+分別為v∞-,v∞+與大氣邊緣的夾角。Δθd,Δθe,Δθa分別為下降段、平飛段和上升段飛過的角度。

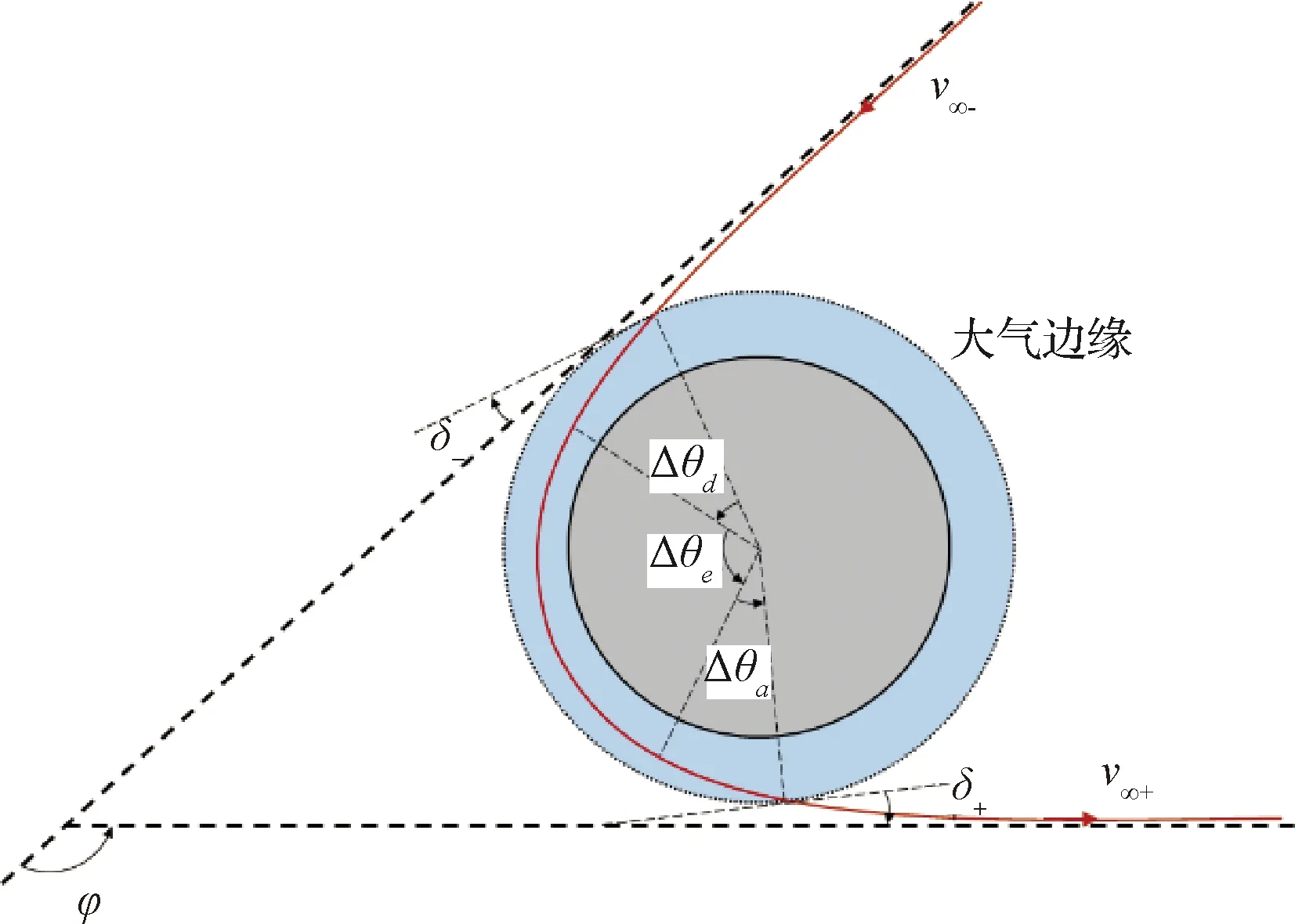
圖5 氣動引力輔助速度偏轉角

從圖5幾何關系可以看出，氣動引力輔助過程中總速度偏轉角為，

φ=δ-+Δθ+δ+=δ-+Δθd+Δθe+Δθa+δ+

(20)

式中:δ-,δ+可通過經典軌道力學計算得到，

(21)

式中:e,f為雙曲線軌道的偏心率和航天器的真近點角，可使用以下公式計算，

(22)

將航天器進入大氣以及飛出大氣時的v,r,γ代入即可計算得到δ-,δ+。

1.3 軌道優化模型

對于自由返回軌道，航天器從地球出發，經過N次借力飛行最終返回地球。因此進行軌道優化時，最小化目標函數為

(23)

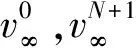
對于引力輔助的自由返回軌道，優化變量取為t0,t1,…,tN,tN+1;r1,…,rN。其中，t0,tN+1分別為地球出發和返回時間；t1,…,tN和r1,…,rN為到達各借力天體的時間和近心距。

約束條件為

(24)

即地球出發時間t0在2033年到2036年范圍內，各天體處近心距應至少高于天體半徑200 km，且雙曲剩余速度在引力輔助前后不改變大小。

對于氣動引力輔助的自由返回軌道，優化變量取為t0,t1,…,tN,tN+1; Δθ1,…,ΔθN;γ1,…,γN。其中,Δθ1,…,ΔθN和γ1,…,γN分別為各借力天體處大氣飛行角和進入大氣時的航跡角。

約束條件為

(25)

2 軌道優化結果

本節研究了“地球-火星-地球(E-M-E)”、“地球-火星-金星-地球(E-M-V-E)”和“地球-金星-火星-地球(E-V-M-E)”三種火星自由返回軌道序列。金星的質量和軌道特性使其成為載人火星任務的首選引力輔助天體[6]，因此在后兩種序列中，利用了金星引力輔助實現自由返回軌道。研究中分別對比了采用引力輔助模型、本文提出的三段式氣動引力輔助模型和現有文獻中簡化氣動引力輔助模型[17]的優化結果。

2.1 E-M-E序列

E-M-E序列只需要一次借力飛行，是最簡單的火星自由返回軌道。航天器從地球出發，進入火星轉移軌道。如果任務正常進行，則可以在火星近拱點處減速，進入環火軌道。如果任務終止，則不進行減速制動，直接返回地球。根據第1.3節優化模型搜索得到的燃料最優自由返回軌道如圖6所示。

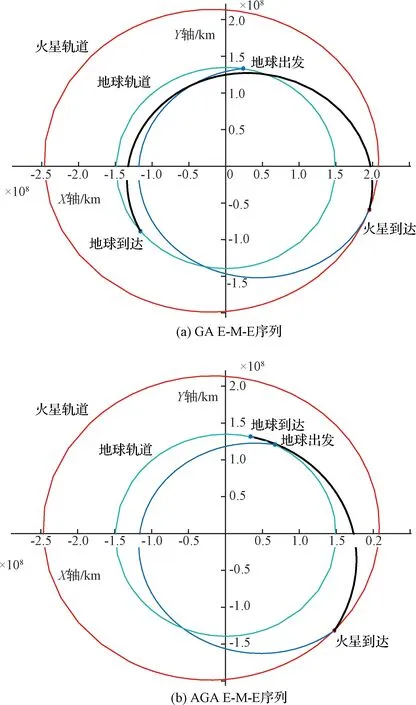
圖6 E-M-E自由返回軌道

轉移軌道參數比較見表1，其中GA為采用引力輔助的軌道，AGA1為采用三段式氣動引力輔助模型的軌道，AGA2為采用簡化氣動引力輔助模型的軌道。

對比GA和AGA1軌道可以發現，使用氣動引力輔助可以將飛行總時間減少125 d，其中返航時間可以減少102 d，因此非常適合需要快速返回地球中止軌道任務，同時燃料消耗減少約2.5 km/s。對比兩種軌道的V∞速度，可以發現V∞E1基本保持不變，V∞M增大了1.21 km/s，而V∞E2減小了3.31 km/s。

對比AGA1和AGA2軌道可以發現，根據本文提出的氣動引力輔助模型計算得到的軌道與現有模型計算得到的軌道參數基本一致，驗證了本文模型的正確性。兩個軌道的主要區別在于AGA1軌道的大氣飛行角ΔθM比AGA2軌道大23°，這主要是由于簡化模型中沒有考慮下降段與上升段對大氣飛行角的貢獻。同時AGA1軌道還給出了大氣飛行段的初始航跡角，可作為高精度氣動引力輔助仿真的初始值。

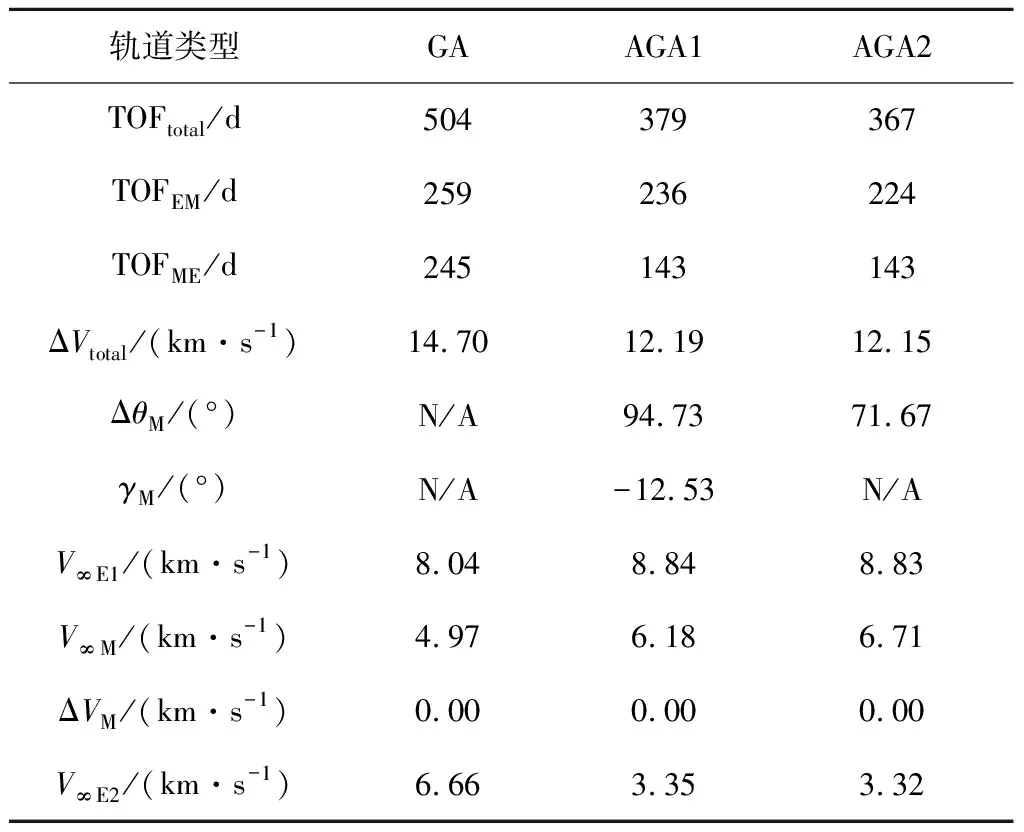
表1 E-M-E自由返回軌道參數Table 1 Parameters of E-M-E free return trajectory

E-M-E自由返回軌道燃料消耗以及V∞速度較大，對火箭運載能力的要求較高，但由于具有出航和返航時間較短的優勢，很適合作為載人任務的軌道。

2.2 E-M-V-E序列

E-M-V-E自由返回軌道到達火星后并不直接返回地球，而是相繼經過火星和金星兩次引力輔助后返回地球。根據第1.3節優化模型搜索得到的燃料最優自由返回軌道如圖7所示。

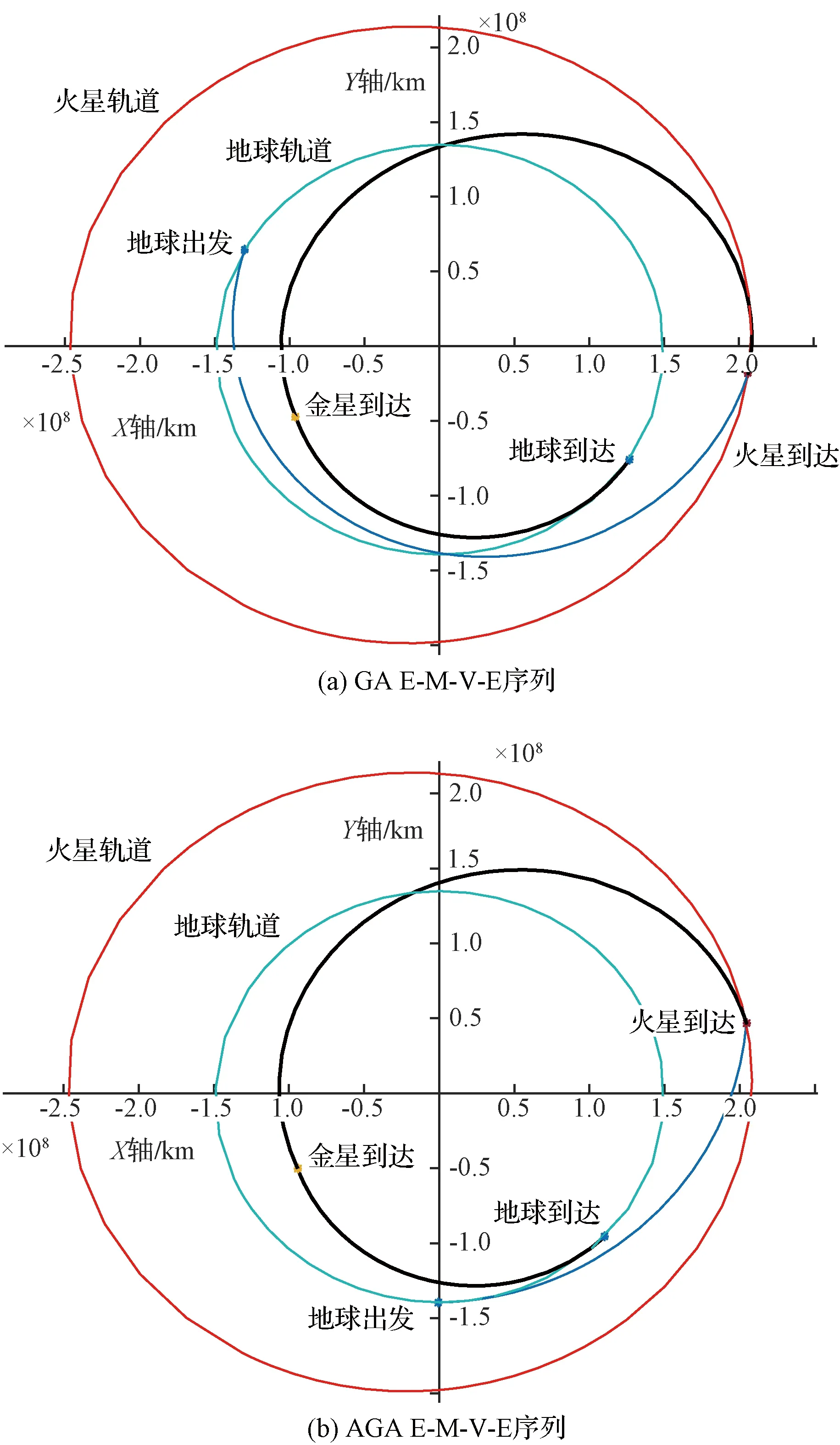
圖7 E-M-V-E自由返回軌道

轉移軌道參數比較見表2，其中GA為采用引力輔助的軌道，AGA1為采用三段式氣動引力輔助模型的軌道，AGA2為采用簡化氣動引力輔助模型的軌道。

對于E-M-V-E自由返回軌道，AGA1在燃料消耗減少1.28 km/s的基礎上，總飛行時間減少132 d。地火轉移時間減少89 d，降低約43%，極大地加快了出航過程。由于到達火星時與火星軌道速度夾角較大，如圖7所示，其V∞M也較大，不利于在火星正常入軌。

AGA軌道在火星處使用了氣動引力輔助技術，而在金星處則僅使用引力輔助。這是由于金星的引力輔助能力較強，可以達到指定的速度偏轉角，如果使用氣動引力輔助，反而會導致速度降低，增加燃料消耗。

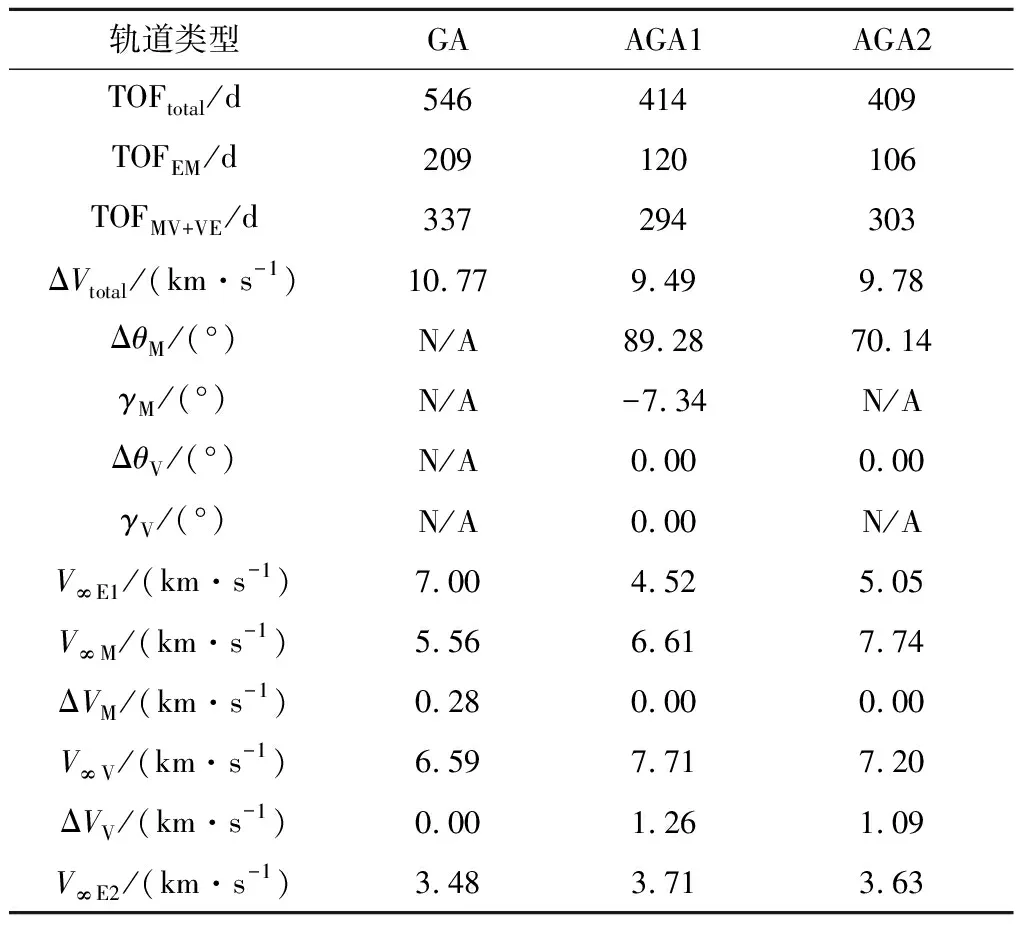
表2 E-M-V-E自由返回軌道參數Table 2 Parameters of E-M-V-E free return trajectory

與第2.1節類似，AGA1與AGA2軌道優化結果基本一致，其中AGA1軌道由于包括下降段和上升段，大氣飛行角比AGA2軌道大。

由于使用了兩次引力輔助，E-M-V-E序列相對E-M-E序列更加復雜，返航時間也更長，不利于故障模式下航天器快速返回地球。但由于其燃料消耗較少，出航時間較短，地球出發和到達V∞速度較低，有利于工程實現。

2.3 E-V-M-E序列

E-V-M-E序列與E-M-V-E序列類似，同樣使用金星引力輔助，區別僅在于到達火星與金星的先后順序，因此其優化過程也與E-M-V-E序列類似。搜索得到的燃料最優自由返回軌道如圖8所示。

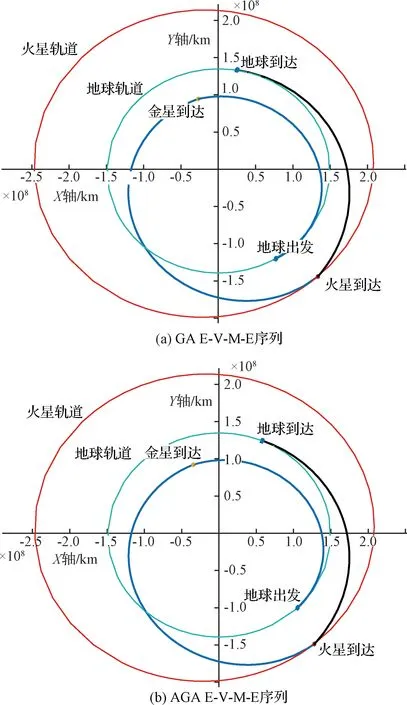
圖8 E-V-M-E自由返回軌道

兩條轉移軌道參數比較見表3。其中GA為采用引力輔助的軌道，AGA1為采用三段式氣動引力輔助模型的軌道，AGA2為采用簡化氣動引力輔助模型的軌道。

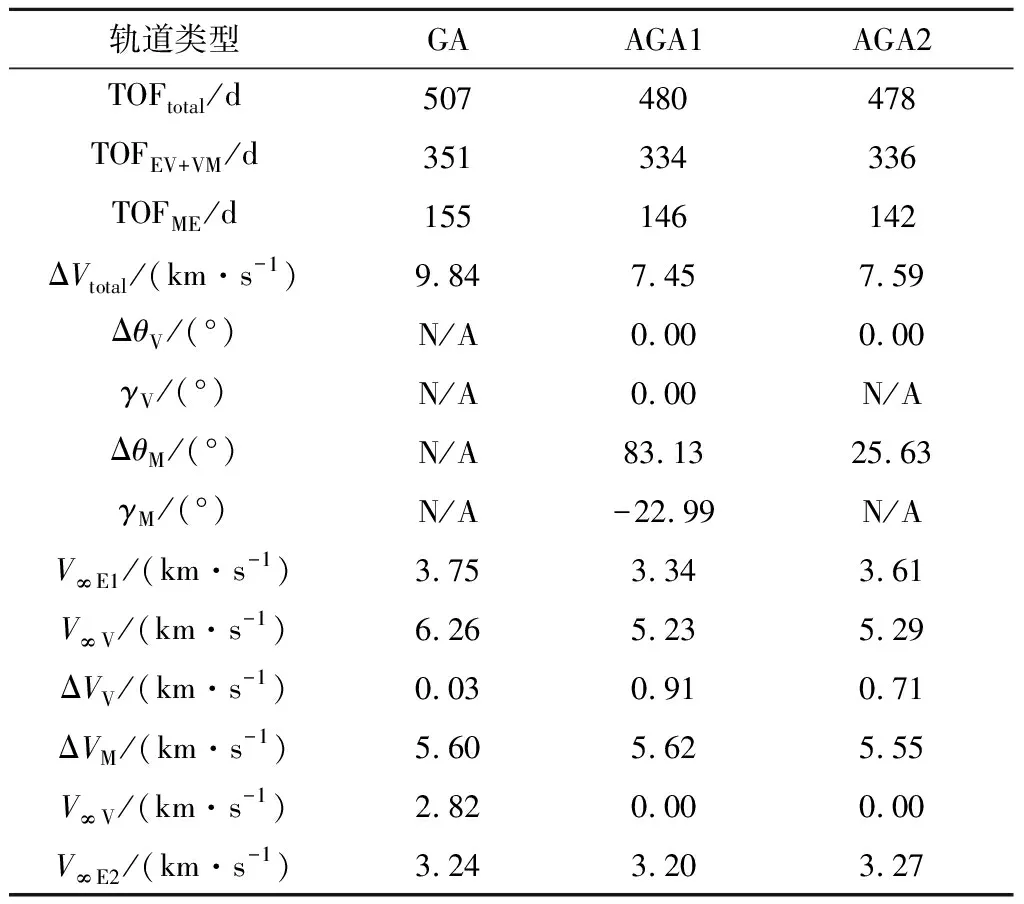
表3 E-V-M-E自由返回軌道參數Table 3 Parameters of E-V-M-E free return trajectory

由表3可知，AGA1在燃料消耗減少約2.4 km/s的基礎上，相對于GA軌道飛行總時間僅減少27 d，效果不如之前兩種序列。這主要是由于金星較強的引力輔助能力使航天器進入較為理想的轉移軌道。

AGA1軌道與AGA2軌道參數基本一致，主要區別在于大氣飛行角的不同，這與前兩節的結論是一致的。

E-V-M-E序列出航時間較長，不利于正常任務的進行，但其較短的返航時間和較小的出發和返回雙曲剩余速度對于故障模式下快速返回地球十分有利，同時其燃料消耗是三種序列中最小的。

3 結束語

本文對基于氣動引力輔助的火星自由返回軌道進行了研究。針對現有研究中氣動引力輔助模型過于簡化，提出將大氣飛行過程分為下降段、平飛段以及上升段三個階段，使用大氣飛行角Δθ和航跡角γ來描述氣動引力輔助過程，并分別建立了各段的計算模型。

本文分別對E-M-E,E-M-V-E和E-V-M-E三種火星自由返回軌道序列進行了計算分析，比較了引力輔助模型、三段式氣動引力輔助模型以及簡化氣動引力輔助模型。計算結果表明，根據本文提出的氣動引力輔助模型計算得到的轉移軌道與現有文獻結果類似，主要區別在于大氣飛行角的大小。現有文獻模型由于忽略了下降段和上升段，其大氣飛行角被明顯低估，而本文提出的模型由于更接近真實的飛行過程，可以更準確地計算出大氣飛行角并給出相應的航跡角。該模型還給出了大氣飛行段的初始航跡角，可作為高精度氣動引力輔助仿真的初始值。計算結果同時表明，對于三種自由返回軌道序列，氣動引力輔助技術可以顯著提升自由返回軌道性能，如降低出航和返航時間，降低燃料消耗等。雖然氣動引力輔助由于其技術上的復雜性而未能在以往的航天任務中得到應用，但隨著航天技術的不斷進步，這種技術必將得到更廣泛的應用。