基于北斗Ka星間鏈路的地面用戶導(dǎo)航方法

肖 洋，李理敏，常家超，余金培，龔文斌，梁 廣

(1. 中國科學(xué)院上海微系統(tǒng)與信息技術(shù)研究所，上海 200050；2. 中國科學(xué)院大學(xué)，北京 100049；3. 上海微小衛(wèi)星工程中心，上海 201203；4. 溫州大學(xué)數(shù)理與電子信息工程學(xué)院，溫州 325035)

0 引 言

精度、完好性、連續(xù)性和可用性是全球衛(wèi)星導(dǎo)航系統(tǒng)的四大關(guān)鍵指標[1]。其中，可用性是指導(dǎo)航系統(tǒng)的用戶可以根據(jù)接收的導(dǎo)航信號獲取自己的位置信息。傳統(tǒng)的L頻段導(dǎo)航信號容易受到各種有意或者無意的干擾和欺騙[2-5]，尤其是一些重點區(qū)域和敏感區(qū)域，在特殊時期將會成為各種干擾源與欺騙源的攻擊目標，導(dǎo)致L頻段導(dǎo)航信號在該區(qū)域?qū)Ш叫阅芟陆瞪踔潦В瑖乐赝{地面用戶的安全。

北斗衛(wèi)星導(dǎo)航系統(tǒng)是我國自主建設(shè)、獨立運行，并與世界其他衛(wèi)星導(dǎo)航系統(tǒng)兼容共用的全球衛(wèi)星導(dǎo)航系統(tǒng)。北斗導(dǎo)航系統(tǒng)設(shè)計了基于Ka頻段的星間鏈路網(wǎng)絡(luò)，可完成星間、星地高精度雙向測量，并具有一定的數(shù)據(jù)傳輸能力，已成功應(yīng)用于北斗導(dǎo)航星座的自主運行及測控管理[6-10]，利用其富裕資源為地面L頻段導(dǎo)航信號失效區(qū)域提供導(dǎo)航定位服務(wù)具有重要意義：一方面能避開針對L頻段導(dǎo)航信號的干擾和欺騙，有效彌補L頻段導(dǎo)航信號失效帶來的缺失，另一方面北斗Ka星間鏈路信號載波頻率高，信號傳輸幾乎不受電離層影響[11]，因此可提供精度更高的測距值。

本文首先對利用北斗星間鏈路信號為地面特定區(qū)域提供導(dǎo)航服務(wù)進行了可行性分析；然后給出了地面用戶基于北斗星間鏈路信號的測距模型；針對時分體制下測距值時間不同步的問題，提出借助慣導(dǎo)信息以及用戶鐘差模型對測距值進行歷元歸算，并在此基礎(chǔ)上推導(dǎo)了基于北斗星間鏈路信號的實時定位算法，最后通過仿真分析驗證了算法的性能。

1 可行性分析

北斗星間鏈路采用時分體制[12-13]，每顆衛(wèi)星按照預(yù)定路由規(guī)劃表在不同時隙通過調(diào)整其相控陣天線波束指向與其他衛(wèi)星或地面站構(gòu)建星間、星地鏈路[14]。假設(shè)T1～T5分別代表五個連續(xù)的時隙，表1為北斗衛(wèi)星路由規(guī)劃表示例。其中Si代表衛(wèi)星號，S代表地面站，符號‘-’表示該時隙為空閑時隙。圖1給出了衛(wèi)星S1按照表1所示的路由規(guī)劃表先后與衛(wèi)星S7、地面站S以及衛(wèi)星S3的建鏈過程。

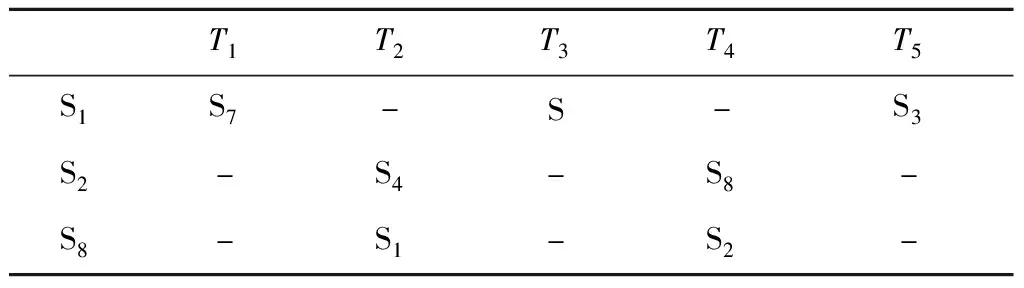
表1 北斗星間鏈路路由規(guī)劃表示例Table 1 An example for the Routing table of Beidou inter-satellite links

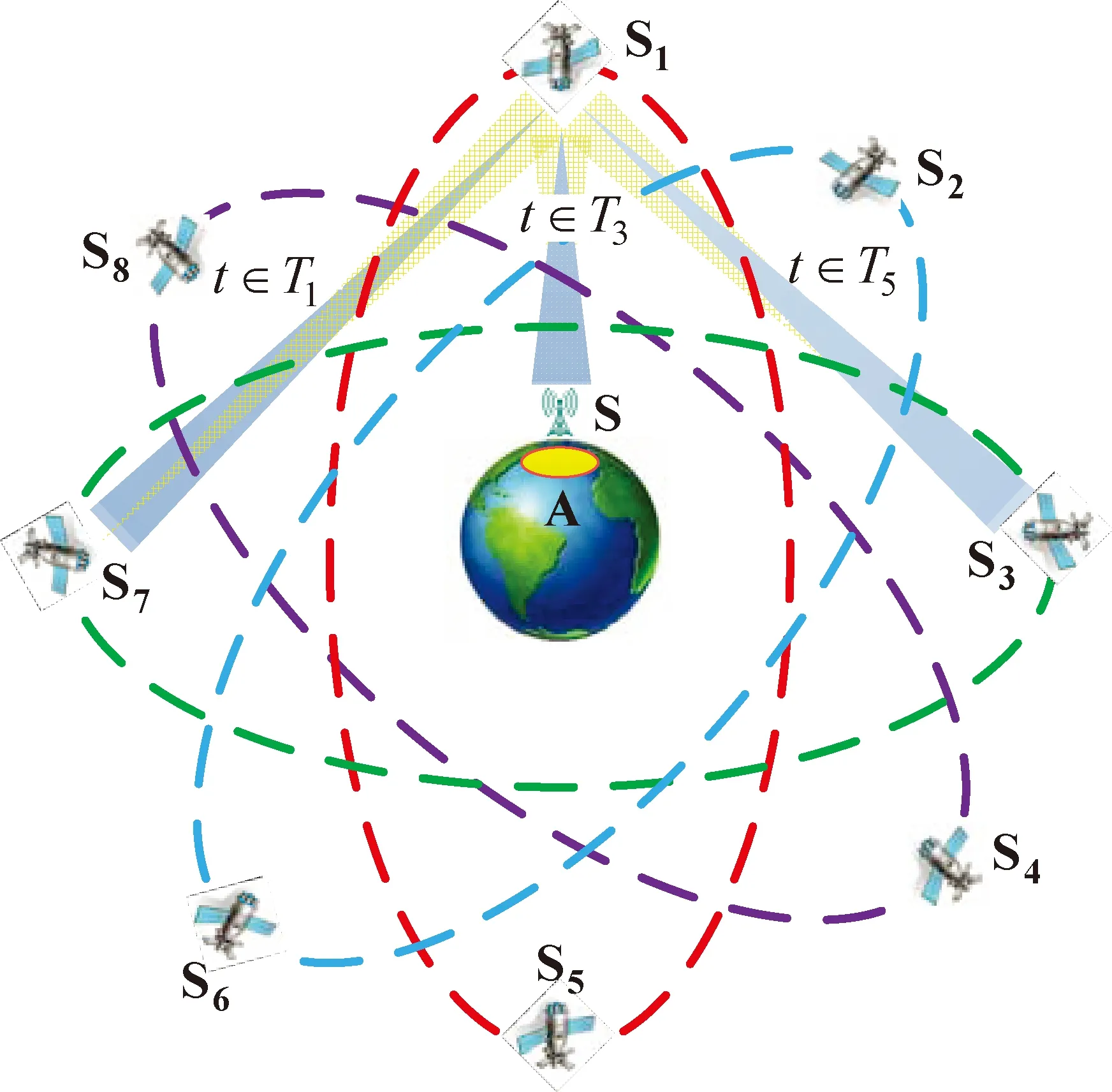
圖1 北斗星間鏈路時分體制下星間、星地雙向測量

在現(xiàn)有體制下，北斗星間鏈路仍有比較充裕的空閑時隙。假如地面A區(qū)域L頻段導(dǎo)航信號失效，A區(qū)域內(nèi)的用戶通過地面應(yīng)急通信方式將該區(qū)域位置告知地面主控站S，S隨即重新規(guī)劃星間鏈路路由規(guī)劃表，并將其上注至視線范圍內(nèi)的北斗衛(wèi)星S1，S1利用北斗星間鏈路的通信功能將新的路由規(guī)劃表廣播至所有北斗衛(wèi)星。根據(jù)表1可知，其上空的衛(wèi)星S8、S1、S2分別在時隙T1、T2、T3空閑。因此，在星間鏈路路由規(guī)劃表中將衛(wèi)星S8、S1、S2的波束分別在時隙T1、T2、T3指向區(qū)域A，并廣播下發(fā)星間路由規(guī)劃表信息，如圖2所示。對于失效區(qū)域A內(nèi)的地面用戶來說，可通過兩種方式來調(diào)整自己的天線指向以便對準目標衛(wèi)星：1)當?shù)孛鎽?yīng)急通信系統(tǒng)可用時，可通過地面應(yīng)急通信系統(tǒng)獲取北斗衛(wèi)星的相關(guān)信息；2)當?shù)孛鎽?yīng)急通信系統(tǒng)不可用時，地面用戶可根據(jù)預(yù)先內(nèi)置或?qū)Ш绞矮@取的衛(wèi)星歷書信息，調(diào)整波束跟隨指向視線范圍內(nèi)的某顆北斗衛(wèi)星直至收到其信號，并獲取其下發(fā)的星間路由規(guī)劃表信息。因此，利用北斗星間鏈路的空余時隙為地面用戶提供導(dǎo)航服務(wù)是可行的。

2 基于北斗Ka星間鏈路的用戶測距模型

假設(shè)在Tk-1與Tk兩個歷元之間，地面某區(qū)域裝載有北斗星間鏈路終端的用戶分別在不同時刻與不同N顆北斗衛(wèi)星產(chǎn)生星間鏈路單向測距值，測距方

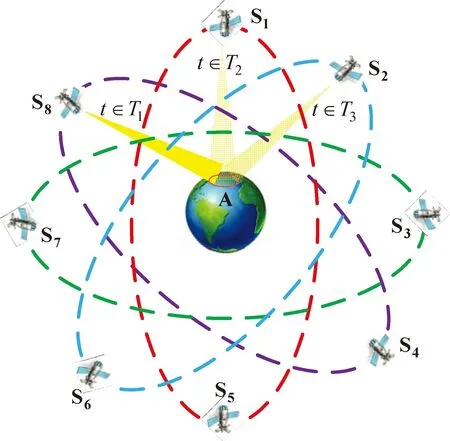
圖2 利用北斗星間鏈路空余時隙服務(wù)于地面區(qū)域

程為

(1)

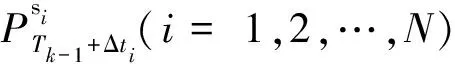
(2)

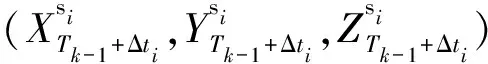
b(t)=a0+a1t+ε

(3)

式中，b(t)代表接收機鐘差，a0代表接收機鐘差初始值，a1代表接收機鐘飄，ε可視為零均值高斯白噪聲，因此有

bTk-1+Δti≈bTk-a1,Tk(Tk-Tk-1-Δti)

(4)

利用慣導(dǎo)系統(tǒng)可以得到用戶從Tk-1+Δti時刻到Tk時刻的位置變化量為

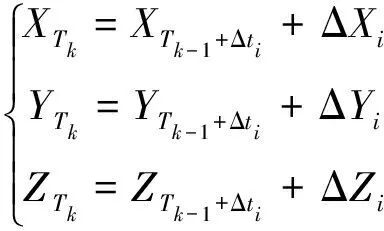
(5)

式中：

(6)

式中，Vx(t)、Vy(t)、Vz(t)分別代表用戶的三維速度。將式(4)和式(5)代入到式(1)和式(2)，即可將觀測方程中用戶的位置統(tǒng)一歸算到Tk時刻，從而實現(xiàn)測距值時間同步，如式(7)和式(8)所示，其中對流層延時使用高精度模型予以校正。

(8)

由于對流層模型存在誤差，且歷元歸算過程也會引入誤差，因此式(7)中的誤差項用νi來表示。由于廣播星歷廣播的是L鏈路信號對應(yīng)的天線相位中心位置及通道時延，當?shù)孛嬗脩羰褂没诒倍稫a星間鏈路測距值定位時，將存在天線相位中心偏差、通道時延偏差等系統(tǒng)偏差[15-16]。為了消除這些系統(tǒng)偏差對定位結(jié)果的影響，可預(yù)先在地面對其標定或者星上實時標定然后下發(fā)給地面用戶，本文暫不考慮這些系統(tǒng)偏差對定位結(jié)果的影響。

3 基于北斗Ka星間鏈路地面用戶定位算法

在實現(xiàn)測距值時間同步的基礎(chǔ)上，地面用戶即可采用卡爾曼濾波定位算法實時估算自己的位置，選取的狀態(tài)量為

(9)

式中：δr代表對地面用戶三維位置估計的偏差，δv代表對地面用戶三維速度估計的偏差，δb代表對接收機鐘差、鐘飄估計的偏差。與δr、δv相關(guān)的狀態(tài)轉(zhuǎn)移矩陣Φrv為

(10)

式中：Δt代表歷元間隔時間，與δb相關(guān)的狀態(tài)轉(zhuǎn)移矩陣為

(11)

因此，系統(tǒng)狀態(tài)轉(zhuǎn)移矩陣Φk,k-1為

(12)

式中：0m×n代表m×n階零矩陣，系統(tǒng)過程方程為

xk=Φk,k-1xk-1+wk-1

(13)

式中：下標“k”代表歷元時刻，wk-1代表過程噪聲，系統(tǒng)觀測方程為

yk=Hkxk+vk

(14)

式中：Hk為觀測矩陣，可由式來描述，yk為觀測量，可由式(17)來描述，vk為觀測噪聲。

Hk=

(15)

式中：

(16)

(17)

(18)

(19)

式中：右上標“-”和“+”分別表示對狀態(tài)量估計的先驗值和后驗值，Qk-1為過程噪聲的協(xié)方差矩陣。

在更新步驟，狀態(tài)量及其協(xié)方差矩陣變化為

(20)

(21)

(22)

式中：Kk為卡爾曼濾波增益，Rk為過程噪聲的協(xié)方差矩陣。

4 算法性能仿真

利用軌跡發(fā)生器產(chǎn)生的數(shù)據(jù)對上述算法進行性能初步仿真。仿真軌跡如圖3所示，載體初始位置設(shè)為東經(jīng)110°、北緯30°、高度為0 m，初始橫滾角、俯仰角、航向角均為0°，在東向、北向和天向的初始速度均為0 m/s，為不失一般性，載體運動軌跡包括勻加速直線運動、勻速直線運動、爬升、等高轉(zhuǎn)彎、俯沖等過程，仿真時間為3 600 s。假設(shè)慣導(dǎo)系統(tǒng)中三個陀螺儀零偏均為0.1(°)/h，隨機漂移均為0.1(°)/h，三個加速度計的零偏均為10-4g，隨機漂移均為10-4g，接收機時鐘隨機誤差設(shè)為0.1 m。對流層模型誤差設(shè)為0.5 m，使用精密星歷(包括精密軌道星歷和精密鐘差星歷)來模擬測距值，實際定位過程中使用廣播星歷，Ka頻段測距誤差為0.1 m[6]。

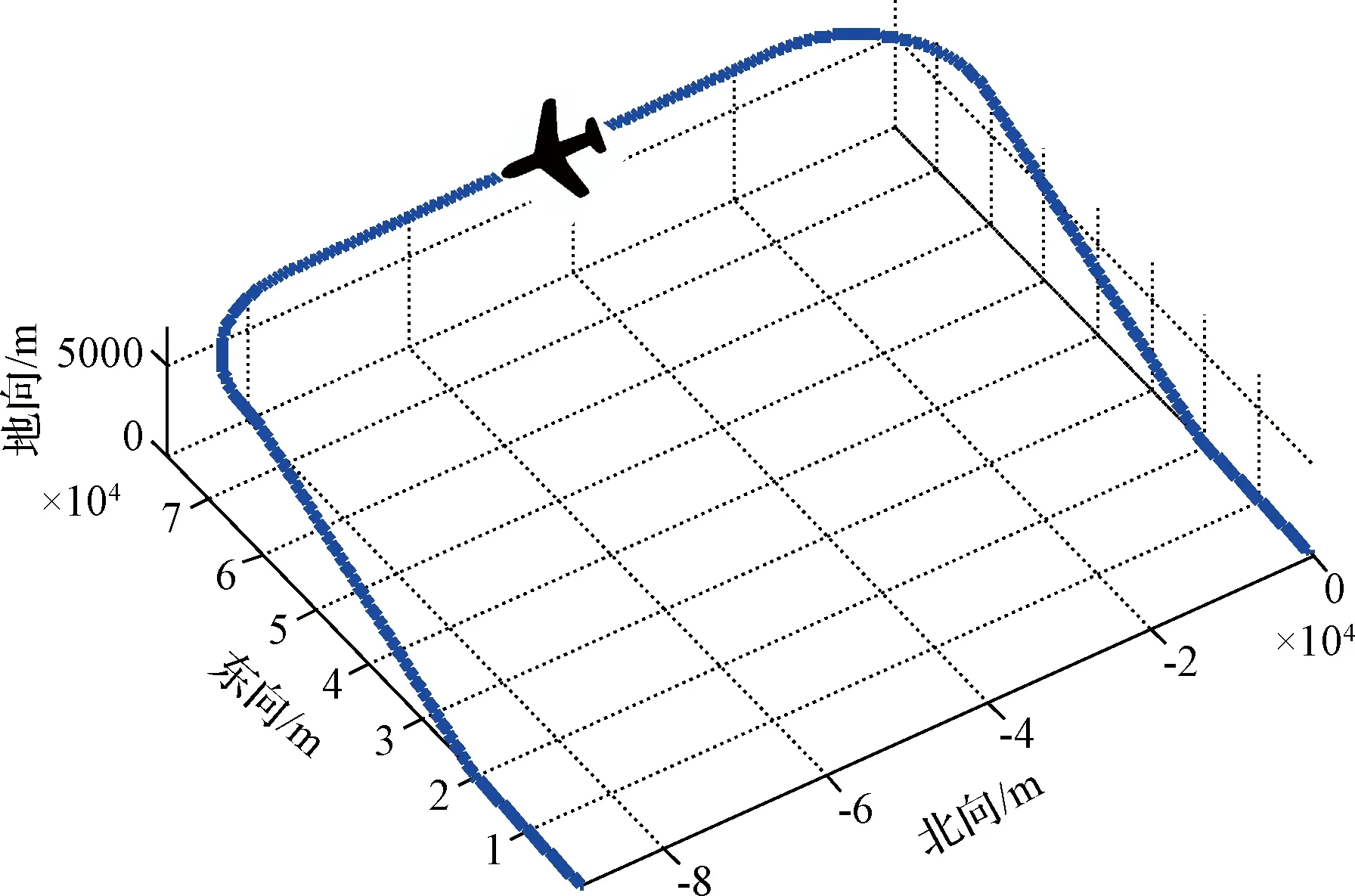
圖3 地面用戶軌跡仿真

使用STK軟件對北斗星座進行軌道仿真，當遮蔽角取15°時，可見星數(shù)目為6～10顆。設(shè)歷元間隔Δt為30 s，假定在每個歷元間隔內(nèi)所有可見星都可以指向地面一次。在相同可見星以及對流層模型誤差情況下，將本文算法與傳統(tǒng)基于L頻段信號的定位算法進行比較，設(shè)L頻段測距誤差為0.8 m(已通過雙頻組合消除電離層影響)。兩種算法在導(dǎo)航坐標系中北、東、地三個方向誤差曲線分別如圖4～圖6所示，三維位置誤差曲線如圖7所示。L頻段定位算法在北、東、地三個方向的誤差分別為0.86、0.72、1.58 m，三維位置誤差為1.94 m，本文算法在北、東、地三個方向誤差分別為0.79、0.60、1.44 m，分別提高了8%、16%、9%，三維位置誤差為1.75 m，提高了10%。

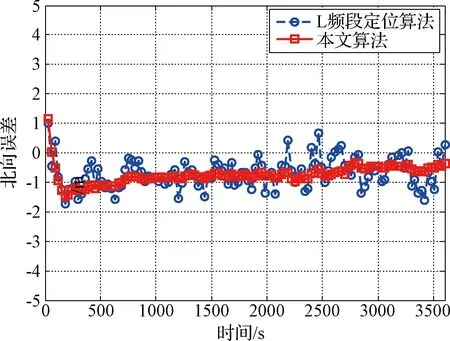
圖4 兩種算法北向誤差曲線

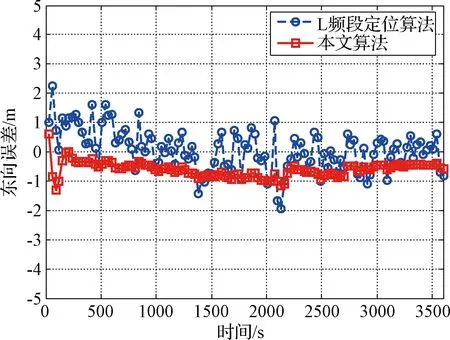
圖5 兩種算法東向誤差曲線

圖6 兩種算法地向誤差曲線

圖7 兩種算法三維位置誤差曲線

為了評估接收機時鐘隨機誤差對定位性能的影響，圖8給出了兩種算法在不同時鐘隨機誤差條件下的三維位置誤差曲線。由圖8可知，當時鐘隨機誤差較小時，本文算法定位誤差小于L頻段定位算法；隨著時鐘隨機誤差增大，本文算法定位誤差明顯增加。因為當時鐘誤差較小時，其對歷元歸算過程影響并不明顯，此時測距誤差是影響定位精度的主要因素；隨著時鐘誤差的增加，會導(dǎo)致本文算法觀測值歷元歸算準確性下降，從而使得本文算法對時鐘誤差更為敏感。

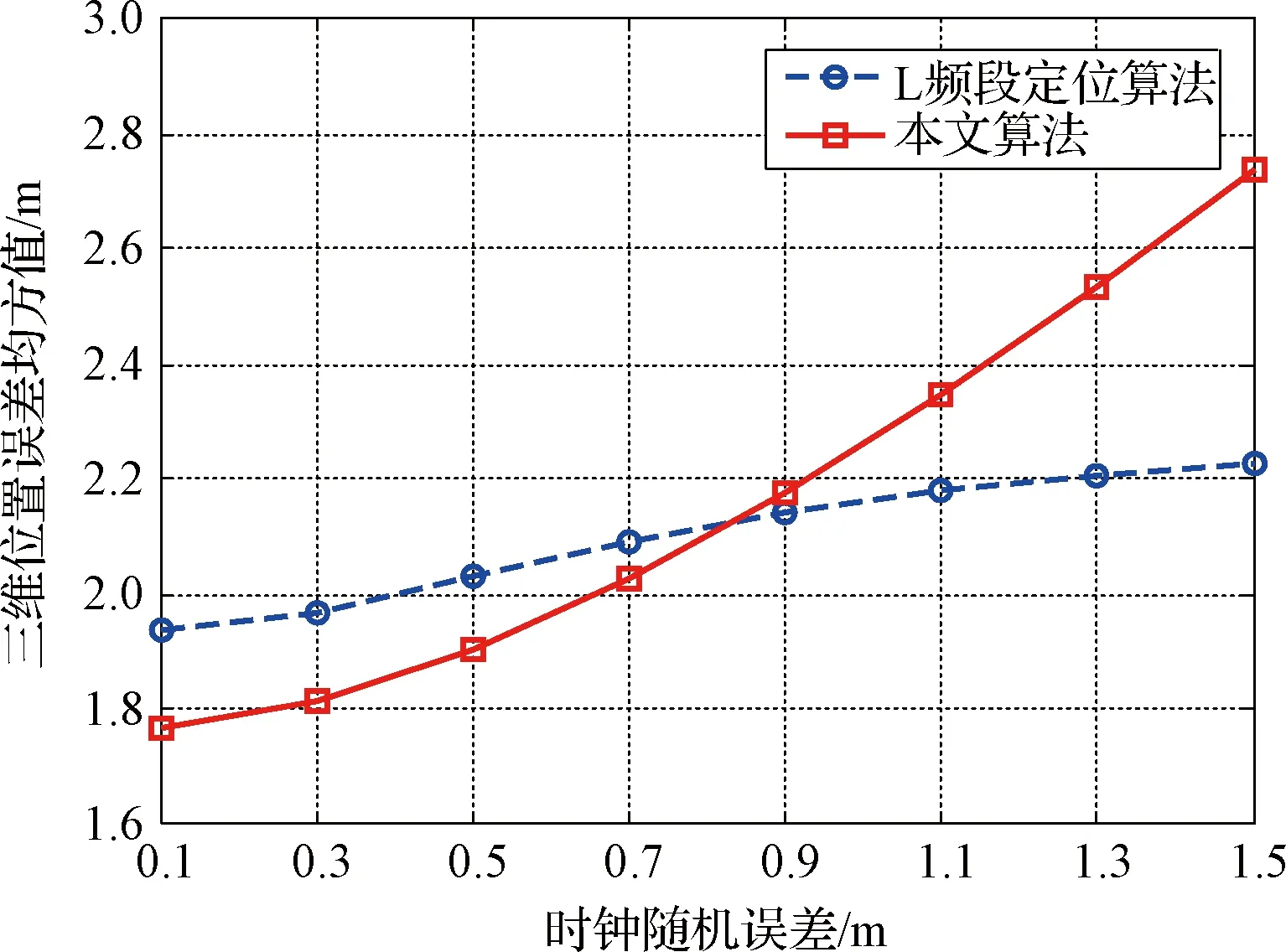
圖8 兩種算法在不同時鐘誤差下的三維位置誤差曲線

為了評估歷元間隔對定位性能的影響，表2給出了兩種算法在歷元間隔分別為30、60、120 s情況下的定位誤差。由表2可知，當歷元間隔增大時，兩種算法定位誤差均呈上升趨勢。相比之下，本文算法隨歷元間隔增大性能下降更加明顯，當歷元間隔為120 s時，L頻段定位算法三維位置誤差增加到2.13 m，而本文算法三維位置誤差增加到3.25 m。另一方面，歷元間隔增大的同時也會降低對星間鏈路空閑時隙的消耗。因此，實際情況中需要綜合考慮歷元間隔對定位性能以及星間鏈路時間資源消耗的影響。

為了評估慣導(dǎo)系統(tǒng)誤差參數(shù)對定位性能的影響，表3給出了兩種算法在初始值和20倍初始值這兩種情況下的定位誤差。由表3可知，當慣導(dǎo)系統(tǒng)誤差參數(shù)增加為原來20倍后，L頻段定位算法在北、東、地三個方向上的誤差分別增加了5%、4%、2%，三維位置誤差增加了3%；而本文算法在北、東、地三個方向上的誤差分別增加了15%、18%、37%，三維位置誤差增加了30%。由于慣導(dǎo)系統(tǒng)誤差參數(shù)同樣會影響過程噪聲以及歷元歸算誤差，因此，相比之下本文算法對慣導(dǎo)系統(tǒng)誤差參數(shù)更加敏感。

在上述仿真過程中，鏈路數(shù)目與可見星數(shù)目保持一致，即6～10條。為了評估鏈路數(shù)目對算法性能的影響，表4給出了兩種算法在鏈路數(shù)目分別為6～10條、只選6條、只選5條三種情況下的定位誤差。由表4可知，當鏈路數(shù)目減少時，由于觀測量數(shù)目減小，L頻段定位算法與本文算法定位精度均有所下降。因此，為了提高定位精度，應(yīng)盡可能為地面用戶分配更多的鏈路。

表2 不同歷元間隔定位誤差均方值Table 2 The root-mean-square (RMS) of position errors with different epoch intervals (m)

表3 不同慣導(dǎo)系統(tǒng)誤差參數(shù)定位誤差均方值Table 3 The RMS of position errors with different error parameters of INS (m)

表4 不同鏈路數(shù)目下定位誤差均方值Table 4 The RMS of position errors with different number of links (m)

5 結(jié) 論

本文根據(jù)北斗Ka星間鏈路的特點，提出了一種利用星間鏈路信號為地面L頻段導(dǎo)航信號失效區(qū)域提供導(dǎo)航定位服務(wù)的方法。利用鐘差模型和慣導(dǎo)系統(tǒng)解決測距值時間不同步的問題，并在此基礎(chǔ)上推導(dǎo)了基于北斗Ka星間鏈路信號的實時定位算法。仿真結(jié)果表明：當歷元間隔為30 s時，本文算法定位精度可以達到2.0 m以內(nèi)。與此同時，本文還詳細分析了接收機時鐘隨機誤差、歷元間隔、慣導(dǎo)系統(tǒng)誤差和鏈路數(shù)目等因素對算法定位性能的影響。本文方法能夠在一定程度上彌補L頻段導(dǎo)航信號失效帶來的可用性問題，保障重點區(qū)域在特殊場景下的導(dǎo)航安全。