基于假設檢驗理論的雷達近鄰目標距離統計分辨限

張云雷 湯 俊 王 力

①(清華大學電子工程系 北京 100084)

②(海軍工程大學電子工程學院 武漢 430033)

1 引言

分辨問題是雷達系統的基本問題之一。傳統方法是利用波形模糊函數來定義分辨限[1]，即考察特定波形在和理想目標回波(含距離時延和多普勒調制)匹配濾波后響應函數波峰的3 dB或4 dB寬度，由此來確定該雷達波形對應的距離分辨率和多普勒分辨率，一般工程實踐中將這個寬度對應的分辨率限稱為瑞利限，并認為實際中當兩個目標的時延間隔或者多普勒差異在瑞利限以內時，將無法分辨。兩線性調頻(LFM)信號在時間上相距瑞利限內間隔時匹配濾波結果會產生相加混疊效果。如圖1所示，兩目標距離為0.5/B時(B為信號帶寬)，匹配濾波只能得到1個峰值，而當兩目標的距離達到1.5/B時出現2個峰值。因此，目前在雷達的工程實踐中，一般采用模糊函數分析方法，距離上相近目標可分辨的瑞利限定義為δrayleigh=1/B。

圖1 兩線性調頻信號相關的單次蒙特卡洛仿真Fig.1 Monte Carlo simulation of the correlation result of two LFM signals

采用傳統模糊函數分析方法可以得到某種雷達波形所對應的確定性分辨率指標，但是需要進一步探究以下問題：第一，傳統的模糊函數分辨限分析方法基本出發點是采用匹配濾波來處理回波信號，匹配濾波在白噪聲和點目標前提下使得輸出信噪比最大，對檢測來說最優，并不適用于多個目標的分辨問題；第二，模糊函數分析方法并不能反映出噪聲、目標起伏等隨機因素、以及近距多目標波形相互干擾等因素的影響；第三，模糊函數分析方法只能對兩個相同信噪比的目標給出分辨率的結論，但不適用于實際中經常存在的不同信噪比的多個目標的分辨。

在一些相關的領域如波達方向角(DOA)、功率譜、空間譜估計中，已經開展了大量高分辨理論和算法的研究，并實現了對瑞利限的突破[2-4]。因此，有必要對傳統雷達模糊函數分析方法所確定的雷達波形分辨率分析方法做進一步的探討和研究。

為便于分析，本文采取如下研究思路：

(1) 對雷達分辨問題場景簡化：一是先僅考慮距離分辨問題，即忽略多普勒分辨問題。如果1維距離分辨問題可以得到解決，則推廣到2維的場景即是一個相對比較自然的過程。二是先考慮兩個目標的分辨問題，因為一旦兩個目標的問題解決，多目標分辨問題可以自然外推；

(2) 對雷達分辨問題模型簡化：對于接收機收到的兩個和噪聲相混疊的雷達目標回波，存在兩種不同的分辨問題定義：(a)分辨模型1-通過處理，判定存在兩個目標，但不需要同時估計出兩個目標的位置，因為一旦有了兩個目標存在的先驗信息，有很多超分辨算法用于實現位置的估計。(b)分辨模型2-通過處理，判定存在兩個目標，同時兩個目標位置的估計值也滿足準確性要求，如誤差小于某個閾值。可以發現，分辨模型2比分辨模型1的要求更高，因為其將目標數估計和目標參數估計問題同時進行了考慮，分析也更為復雜。所以，為簡化問題，本文暫時只考慮分辨模型1；

(3) 對待分辨信號形式進行前推：在工程實踐中，經常首先實現對回波信號的匹配濾波以最大化輸出信噪比。最大化輸出信噪比對于目標檢測在理論上已經證明是最優的，但是輸出高信噪比對于近鄰目標的分辨是否一定是最有利，這個問題還是存疑的。因為在高信噪比條件下，兩個目標匹配濾波的響應函數之間的相互影響也會更加嚴重，甚至有可能會導致分辨性能下降。因此，本文直接對原始回波數據進行處理，以去除匹配濾波可能帶來的影響；

(4) 把分辨問題看成是一個統計問題：由于噪聲、目標起伏等隨機因素的存在，雷達中目標分辨問題實際是一個隨機問題，存在正確分辨概率和錯誤分辨概率。而傳統的模糊函數分析法沒有考慮到隨機性，只能給出一個確定性的分辨率指標，這對指導實際的雷達系統性能測試和標定等存在一定的問題。本文明確提出統計分辨率的概念，并給出正確分辨概率和錯誤分辨概率的表達式，這對于工程實踐將具有指導意義。

本文將分辨看作是一個統計問題，研究目標是統計分辨限(Statistical Resolution Limit， SRL)。當前，和統計分辨率相關的研究工作主要有兩個方向：

一是直接從目標參數估計的準確性出發，對統計分辨率進行研究[5-8]。如文獻[5]針對多個不同頻率信號的分辨問題，直接基于目標參數估計的統計下界克拉美羅界(Cramer-Rao Bound， CRB)來定義，并將系統的分辨率表示為pmink其中參數p為恒定系數，θk為待分辨參數。文獻[6]考慮到兩信號之間的耦合，將上述定義擴展到待分辨參數間隔的統計下限，為文獻[7]則從多維統計分辨角度更深入地描述了該問題。文獻[8]討論了近場條件下基于CRB定義的統計分辨限。總體來看，基于CRB定義的SRL反映了對參數估計的準確程度，具有一定物理意義，但該類方法需假定目標個數已知，同時在參數p的選擇上存在一定的主觀性，并不能直接應用于實際雷達目標的距離分辨問題中來。

二是采用假設檢驗理論來研究分辨問題。如文獻[9]研究了白噪聲中兩頻率相近正弦信號的頻率統計分辨問題，并與MUSIC方法超分辨性能進行了比較。文獻[10]推導了高斯白噪聲條件下3維空間中兩近鄰目標的方位SRL，并采用廣義似然比(GLRT)統計量獲得了漸進分辨性能，推導了分辨限與CRB的關系。EL KORSO等人[11]針對被動陣列應用場景，系統地研究了存在點源干擾條件下兩空間近鄰目標的方位統計分辨限。文獻[12]基于信息論準則，討論了兩方位近鄰目標的統計分辨性能。文獻[13]則將相關研究從GLRT檢測擴展到Rao檢測。文獻[14]針對TR-MIMO雷達討論了方位統計分辨問題。SHAHAM等人[15，16]則假定匹配濾波后響應函數 sinc2(x)，研究光學領域成像的距離統計分辨性能。上述研究工作主要集中在方位和頻率維度的統計分辨性能，圍繞雷達距離統計分辨率研究目前還處于起步階段。

本文針對分辨模型1，采用假設檢驗理論研究雷達近鄰目標的分辨問題：在某一段距離范圍內，假定已經確定有目標存在，需要判定是一個還是兩個目標。

本文采用如下定義：(1)分辨概率-指能夠正確判定存在兩個目標的概率；(2)虛判概率-實際只有一個目標，但判定為兩個目標的概率。通過研究回答以下問題：一是給定雷達波形、兩目標距離間隔和虛判概率，如何計算理論上能夠達到的最大分辨概率。二是給定雷達波形、虛判概率和分辨概率，如何計算理論上能夠達到的最小兩目標分辨極限。

本文中， ( ?)T和( ?)H分別表示向量或矩陣的轉置和共軛轉置，( ?)*表示取共軛操作。?s」代表不超過s的最大整數。L表示維度為L×L的單位陣。R和 C 分 別是實數和復數的集合，R e(?) 和 I m(?)分別為復數的實部和虛部。本文組織如下：第2節介紹問題的模型，第3節開展統計分辨性能的討論和分析，第4節給出仿真結果，第5節進行總結。

2 基于假設檢驗的近距離分辨模型

在考慮分辨問題時，和文獻[9-16]相類似，本文研究前提是判斷出有目標存在。例如可通過匹配濾波處理，得到目標回波的匹配濾波輸出響應，形成有效目標存在性的判決，并粗略判斷出目標回波的中心位置。下面將基于目標存在和中心位置已知的信息，來判斷是一個目標還是兩個目標。

假定雷達發射的基帶復信號為s(t)，兩目標回波幅度分別為α1和α2，注意α1和α2為復數。兩目標回波到達時間分別為t1和t2，即雷達基帶回波信號可表示為x(t)=α1s(t-t1)+α2s(t-t2)， 信號s(t)帶寬為B，時寬為τ ，假定兩回波間隔為t1-t2=δt小于瑞利分辨單元，即δt＜1/B，且兩回波的中心t0=(t1+t2)/2 已知。n(t) 為零均值、方差為σ2的復加性高斯白噪聲。上述分辨問題可以建模為二元假設檢驗問題，表示為

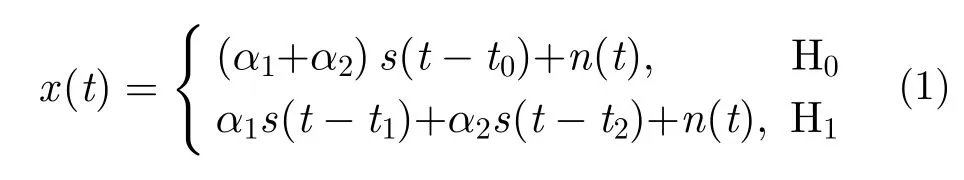
其中，H0假設代表只有一個目標，H1假設代表存在兩個目標。假設檢驗的目標就是要判斷兩信號的時延差δt=t2-t1是否為0。對近鄰目標，假定δt足夠小，令t′=t-t0,α-=α1-α2,α+=α1+α2，將H1表達式在t′處進行泰勒展開保留2階項，可得

對信號及1階、2階導數的波形進行等間隔采樣，采樣頻率fs大于信號帶寬，則采樣點數為L=?τ×fs」。采樣結果為 =[s(1)s(2)???s(L)]T，˙=[s˙(1)s˙(2)???s˙(L)]T和¨=[s¨(1)s¨(2)???s¨(L)]T，以 為高斯白噪聲，=[n(1)n(2)???n(L)]T，則式(2)對應的離散模型為其中，H0假設( δt=0)表示只存在一個目標，H1假設(δt=/0)表示存在兩個目標。由于回波幅度未知，該模型為復合假設檢驗模型，存在未知參數α-,α+和 δt。

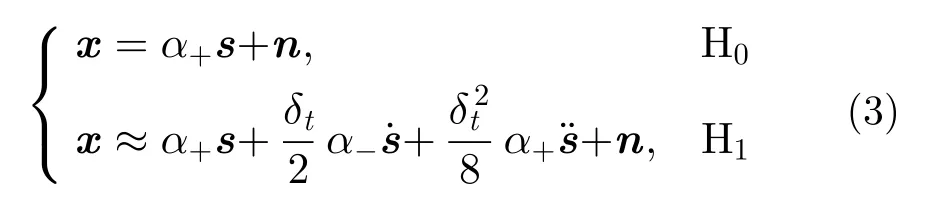
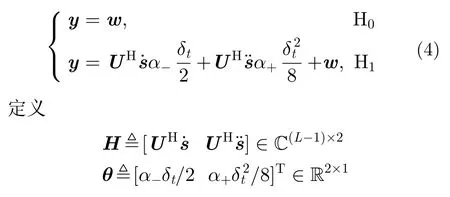
則上述模型可以進一步寫為

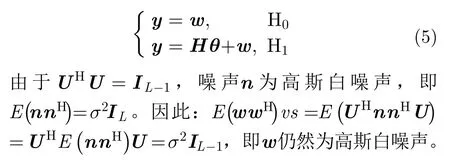
3 分辨統計量及性能分析

當幅度參數 α1,α2確定未知時，最優檢測器為廣義似然比(Generalized Likelihood Ratio Test，GLRT)檢測器，需先求得未知幅度參數的最大似然估計(Maximum Likelihood Estimator， MLE)，再進行似然比檢測。

從式(4)可以看出該模型是復信號的線性假設檢驗模型，則根據統計信號處理相關知識[17]，GLRT對應的統計量為

其中，γ為檢測門限，由給定的虛判概率確定。

一般來說，采樣點數L?2，則從式(5)可得rank=2。記則有rank｛PH｝=2，記P=rank｛PH｝=2，進一步推導得到統計量的分布為[17]

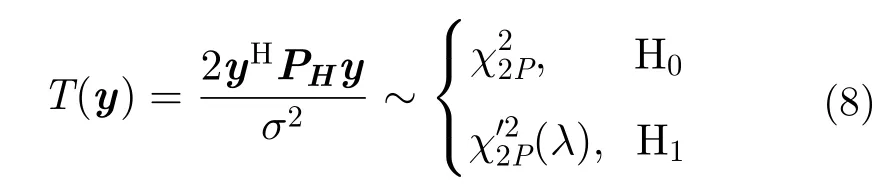
其中，x22P和x22P（λ）分別為自由度2P的中心和非中心卡方分布，其中非中心參數 為[17]

定義信噪比為 ρk=|αk|2/σ2,k=1,2。目標回波幅度相關系數記作c=(α1*α2)/|α1||α2|=cR+jcI，則式(9)可以進一步寫為

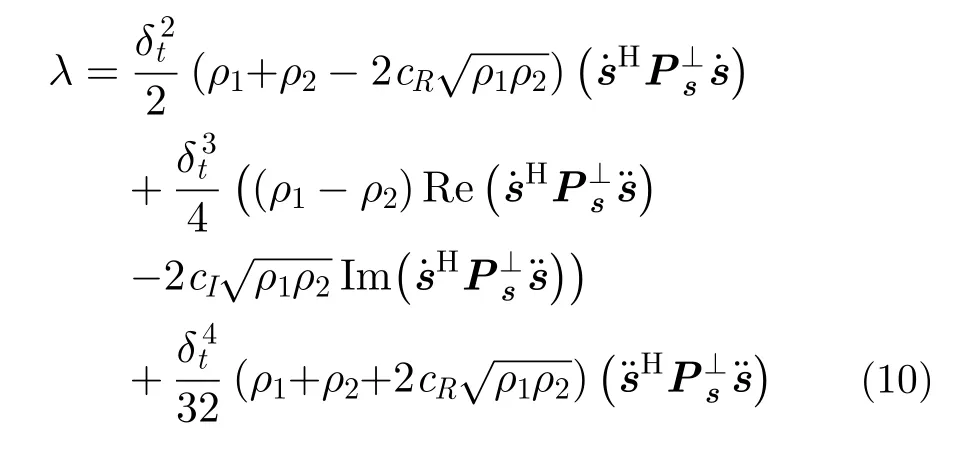
設H0和H1假設下統計量的概率密度函數(PDF)分別為則根據右尾函數的定義[17]，分辨概率和虛判概率可表示為

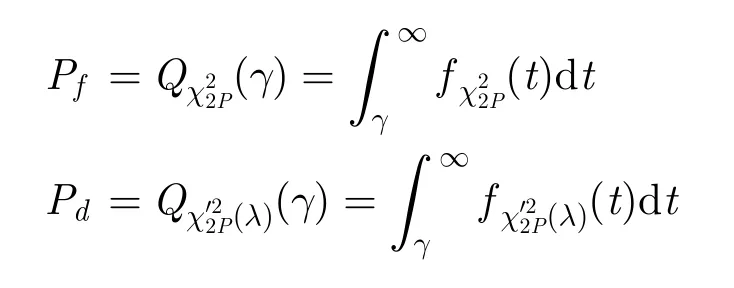
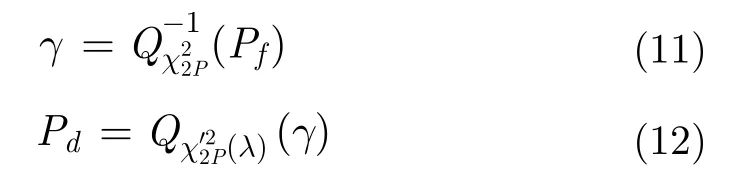
其中，Q-χ221P(?)為Qχ22P(?)的逆函數。

根據上述結果，我們可以實現對雷達應用中兩種典型分辨性能進行分析：

(1) 給定虛判概率Pf，波形，兩個目標信噪比 ρ1,ρ2和 回波幅度的相關系數c，以及預設分辨下限δt，計算出對應的正確分辨概率Pd。步驟如下：

(a) 根據Pf，由式(11)計算判斷門限γ；

(b) 根據， ρ1,ρ2，c和 δt，由式(10)計算非中心參數λ；

(c) 根據λ 和γ，由式(12)計算分辨概率Pd。

(2) 給定虛判概率Pf、分辨概率Pd，波形，兩目標信噪比 ρ1,ρ2和 回波幅度相關系數c，計算能夠實現的分辨下限δt。步驟如下：

(a) 根據Pf，由式(11)計算判斷門限γ；

(b) 根據γ 和Pd，由式(12)逆函數計算非中心參數λ；

(c) 根據λ，s， ρ1,ρ2，c，由式(10)逆函數計算分辨下限δt。

在第(2)種應用中，第(c)步實際要求解式(10)表示的關于分辨限的一個一元四次方程，由于一元四次方程的解存在解析表達[19]故可直接求解，這里我們取其4個根中絕對值最小的實數解作為δt。

4 仿真結果

本節仿真采用的波形為線性調頻(LF M)信號，s(t)=K=B/τ，帶寬和時寬分別為B=106Hz 和τ =10s，采用10倍帶寬采樣，兩信號距離間隔小于瑞利限，信噪比定義為 SNRk=|αk|2/σ2,k=1,2，兩信號的幅度的相關系數c=(α*1α2)/|α1||α2|，虛判概率默認設為Pf=0.001。

仿真1 對比假設檢驗方法與匹配濾波的分辨效果如圖2所示。參數為：兩幅度不相關(即：c=0)信號，間隔分別為0.2， 0.3和0.5倍瑞利限。圖2中關于假設檢驗方法的仿真，保持一個信號的信噪比保持不變(0 dB)，另一個信號的信噪比從-10 dB到10 dB變化。其中分辨概率的數值解是通過對每種信噪比進行1000次蒙特卡洛仿真，根據式(7)計算統計量超過門限 γ次數，除以總次數得到。圖3中的匹配濾波采用兩信號的信噪比均為0 dB，圖中給出的是單次蒙特卡洛隨機仿真的結果。

圖2 假設檢驗和匹配濾波方法的分辨性能對比Fig.2 Comparisons of the hypothesis test and matched filter

從圖2(實線為理論分辨概率，符號為數值分辨率)可看出不同分辨間隔下，假設檢驗方法理論值和數值解基本一致，說明我們的理論結果是正確的。且只要信噪比足夠大，該方法能夠分辨瑞利限內的兩近鄰目標。而從圖3可以看出(虛線表示兩目標的真實位置)，匹配濾波不能分辨瑞利限內的兩近鄰目標。

仿真2 從式(10)可看出，非中心參數 與兩信號幅度的相關系數有關。根據非中心卡方分布的知識[17]，在給定虛判概率下，與分辨概率呈現正相關關系，越大則分辨性能越好。故可以推知分辨概率與相關系數有關。仿真設置兩信噪比為0 dB等功率信號，距離間隔為 δt/δtrayleigh=0.4，變化相關系數c幅度從0到1，相位從- 到，繪制分辨概率如圖4所示。

圖3 匹配濾波方法的分辨性能Fig.3 Performance of matched filter

從圖4(a)可以得出，分辨概率隨兩信號幅度相關系數c的 相位φ =0呈對稱分布。從圖4(b)可以得出，當該相位差較大時，分辨概率隨著c的模增大而提高；但當相位差較小時，分辨概率隨著c的模增大而減小。從圖4(c)可以得出，當兩信號幅度不相關(c=0)時，分辨概率不隨相位變化；而相關時，隨著相位差減小分辨性能變差，其中等相位模為1的兩信號的分辨性能最差。

圖4 分辨概率與相關系數的關系Fig.4 Relationship of the resolution rate and the correlation coefficient

圖5 Pd=0.9時SRL與信噪比的關系Fig.5 Relationship of SRL and SNR withPd=0.9

仿真3 前已提及，分辨性能有2種評價方法，一是給定虛判概率、分辨限和波形參數，確定分辨概率的大小。二是給定虛判概率、分辨概率和波形參數，確定可達到的分辨下限。上面的仿真結果給出了第1種情況的結果。這里將考察第2種情況。假定兩幅度不相關信號(c=0)，設定分辨概率為0.9，虛判概率為Pf=0.001，繪制分辨限隨兩個目標信噪比變化的情況如圖5所示。

由圖5(a)可以看出，和分辨概率相一致，統計分辨限隨信噪比增加而降低，即分辨性能隨信噪比增加而提高。從圖5(b)可以看出，對于幅度不相關，信噪比為0 dB的兩等功率信號，設定0.9， 0.8和0.5的分辨概率，則最高可達0.28， 0.26和0.21倍瑞利限。

仿真4 仍假定兩個幅度不相關的0 dB等功率信號，針對仿真2設置的條件，繪制分辨限與分辨概率和虛判概率的關系，如圖6所示。

由圖6(a)可以看出，當虛判概率一定、要求的分辨概率越小時，或者分辨概率一定、要求的虛判概率越大時，統計分辨極限越小，故分辨性能越好。從圖6(b)和圖6(c)可以看出，當設定虛判概率為0.001和分辨概率為0.5時，利用假設檢驗的分析方法，分辨限最高可達0.3倍瑞利限。

5 結束語

本文采用假設檢驗理論研究兩鄰近目標的統計分辨限，通過深入剖析利用假設檢驗進行臨近目標分辨的意義，給出假設檢驗理論下分辨概率和虛判概率的定義。通過泰勒展開近似和正交投影，將非線性分辨模型轉化為線性檢測模型，進而推導得到了分辨限的解析表達式，基于此討論了影響統計分辨限的各種因素。

圖6 SNR1=SNR2=0 dB時SRL和分辨概率及虛判概率的關系Fig.6 Relationship of SRL and the resolution rate & the false-alarm rate with SNR1=SNR2=0 dB

本文利用線性調頻信號進行了仿真，從結果可以看出，利用統計分辨限的分析方法可以實現對瑞利限的突破。在給定分辨概率和虛判概率下，兩臨近目標的距離統計分辨限不僅與兩信號的信噪比有關，還與兩信號回波的相關系數有關。分辨概率隨信噪比增加而提高，統計分辨下限隨信噪比增加而降低。還可以看出，相關系數的幅度和相位均對分辨性能產生了影響。這些結論對于基于模糊函數的傳統距離分辨性能分析方法均是有益補充，對于解決雷達實際應用中強弱信號同時存在情況下的分辨難題具有參考意義。本文結果表明傳統意義上的低分辨雷達實際具有可達到高分辨性能的很大潛力。

本文僅仿真了線性調頻信號的情況，為簡化分析，假定兩目標回波的中心時刻已知。下面的工作將針對其他類型信號的分辨性能作進一步討論，并擴展到兩目標距離中心值未知的情形以及多目標的情況。