間歇采樣轉發式干擾的時頻域辨識與抑制
周 超 劉泉華 胡 程
(北京理工大學信息與電子學院雷達技術研究所 北京 100081)
(北京市嵌入式實時信息處理技術重點實驗室 北京 100081)
1 引言
基于數字射頻存儲器(Digital Radio Frequency Memory, DRFM)的間歇采樣轉發式干擾(Interrupted Sampling Repeater Jamming, ISRJ),通過對雷達發射信號進行截獲、延時與轉發,可以形成相干干擾[1-4]。此類干擾與雷達發射信號部分相參,能夠在信號處理中獲得一定的增益,大大降低了對干擾機發射功率的需求,為干擾機的小型化和輕量化提供了基礎[5]。因此,此類干擾機可搭載在無人機等小型平臺上,配合蜂群戰術形成主瓣干擾和多點源干擾,增加了雷達反對抗的難度。同時,利用DRFM的數字處理能力,ISRJ干擾機可以方便地對干擾參數進行調節,形成不同的干擾策略,對雷達構成了巨大威脅[6-8]。
對間歇采樣轉發式干擾的研究最早發表于2006年。王雪松等人[9,10]以及Sparrow等人[11]各自提出了間歇采樣重復轉發的干擾策略,并對其性能進行了分析(在文獻[11]中稱為(Chopping & Interleaving, C&I)。該干擾截取雷達發射信號的一個片段進行多次轉發,然后重復截取-轉發過程直至脈沖結束。此干擾信號經過脈沖壓縮處理后,會在距離向上形成多個假目標群,每個假目標群由一個主假目標和多個對稱分布的次假目標組成。通過對信號截取寬度和轉發次數的設計,可以使其兼具壓制和欺騙2種干擾效果。在此基礎上,文獻[10]還提出了間歇采樣直接轉發和間歇采樣循環轉發的干擾樣式。其中,前者對截取的雷達發射信號僅進行一次轉發,但是由于可以截取更多的信號切片,因此干擾能量更強,次假目標也更多;而循環轉發式干擾在轉發當前截獲信號后,還會逆序轉發之前截獲的所有信號片段,其脈壓后的假目標分布范圍更廣、分布規律也更不規則。此后,更多的研究人員對此類干擾的性能進行了分析,并進一步提出了改進的干擾策略。文獻[12]討論了干擾功率損失與截取比例的關系,分析了干擾功率損失對干擾效果的影響。文獻[13]在介紹相參干擾原理及其壓制機理的基礎上,分析了相參干擾的壓制距離。文獻[14]針對線性調頻信號,提出一種截取疊加與移頻調制相結合的相參壓制干擾,在增加假目標數量的同時可使假目標的位置發生變化,從而獲得更佳的干擾效果。
而在雷達抗ISRJ技術方面,相應的研究還比較欠缺。經典的空域抗干擾方法存在難以獲取純凈干擾協方差矩陣和合成波束主瓣性能惡化的難題,因此部分研究人員從波形設計和時頻分析的角度進行了討論。文獻[15]提出使用脈間正交的編碼波形進行干擾抑制,然而該方法僅能對抗脈間轉發式干擾,對于脈內轉發干擾則很難奏效。文獻[16]針對DeChirp雷達,提出使用一種頻域帶通濾波器對干擾進行抑制,主要針對間歇采樣重復轉發和直接轉發式干擾,對濾波的可行性進行了說明,但是對于噪聲水平、干擾參數等因素對濾波器性能的影響,尚未分析。
針對上述問題,本文基于“辨識-剔除”[17,18]的干擾抑制思路,對間歇采樣轉發式干擾的抑制方法進行了研究。針對3種典型的干擾策略,在信號建模的基礎上,推導了干擾信號脈沖壓縮與時頻分布的表達式;并根據其時頻分布的特征差異,設計了干擾辨識流程;進而在獲知目標位置的基礎上,設計時頻域濾波器進行干擾抑制;最后通過仿真對算法的有效性及不同信噪比條件下的性能進行了驗證與分析。
2 間歇采樣轉發式干擾信號模型與干擾機理分析
2.1 干擾信號模型
典型間歇采樣轉發式干擾[9](直接轉發、重復轉發和循環轉發)的工作原理如圖1所示。其中,直接轉發與重復轉發式干擾都是對當前截獲到的雷達信號進行轉發,其差別僅在于轉發的次數不同;該截獲-轉發過程會被重復多次,直到雷達脈沖結束。而循環轉發式干擾在轉發當前信號片段后,還會逆序轉發此前截獲的全部信號片段。
考慮3種干擾策略中轉發次數和轉發方式的差異,相應的干擾信號模型可以表示為:

圖1 間歇采樣轉發式干擾工作原理示意Fig.1 The principle of interrupted sampling repeater jamming
(1) 間歇采樣直接轉發式干擾

其中, r ect(?) 為矩形門函數,N為干擾切片個數,TJ為干擾切片寬度,Kr為發射信號調頻率,τ為干擾機到雷達距離引入的延時。
(2) 間歇采樣重復轉發式干擾

其中,M為每個干擾切片被轉發的次數,Tu=(M+1)?TJ為干擾機進行信號截獲的時間間隔。
(3) 間歇采樣循環轉發式干擾

其中,a=(m(m+1))/2-1為相應切片的截獲延時系數,b=(n(n+1))/2+n-1為每個切片進行轉發時的延時系數。
2.2 干擾機理分析
由于間歇采樣轉發式干擾與雷達發射信號具有部分相參性,因此在進行脈沖壓縮處理后,也可以獲得一定的處理增益,形成假目標。以間歇采樣直接轉發式干擾為例,其脈沖壓縮后的幅度響應可以表示為[19]

對式(4)分析可知:(1)因子 s in(Nφ)/sin(φ)由多個切片的疊加產生,當t=k/KrTu,k∈Z時可以取得極大值;(2)因子 sinc(KrTJ(t-TJ))由單個切片的脈沖壓縮產生,其主瓣寬度為2 /(KrTJ)。
因此,對于間歇采樣直接轉發式干擾,其脈沖壓縮結果表現為一個假目標群,群內存在2M+1個(對于直接轉發式干擾即為3個)假目標,各假目標時間間隔1 /(KrTu)且幅度服從sinc函數調制。
對于間歇采樣重復轉發式干擾,其脈沖壓縮結果相當于對式(4)的多次時移,表現為距離向上的多個假目標群,而每個假目標群的特征與直接轉發式干擾相同。而對于間歇采樣循環轉發式干擾,由于不同切片只有在進行初次轉發時才具有相同的轉發時延,在進行第2次及更多次的轉發時,其時延不同。因此脈沖壓縮結果中存在一個假目標群與多個假目標,其中假目標群的分布特征同樣可以用式(4)描述,而多個假目標則等同于時寬為TJ的Chirp信號的脈沖壓縮結果。
3 間歇采樣轉發式干擾的時頻域辨識與抑制
本節在脈沖壓縮的基礎上,使用短時傅里葉變換(Short Time Fourier Transform, STFT)獲取干擾信號的時頻分布,并討論在此基礎上進行干擾辨識與抑制的方法。
3.1 干擾信號的時頻分析與辨識
為便于分析,首先僅考慮一個干擾切片的處理。在式(4)中,令N=1則可以得到1個切片的脈沖壓縮結果
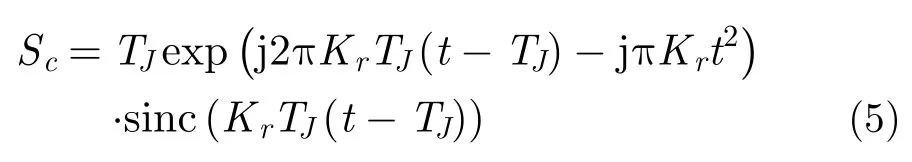
對該信號進行STFT,則可以表示為
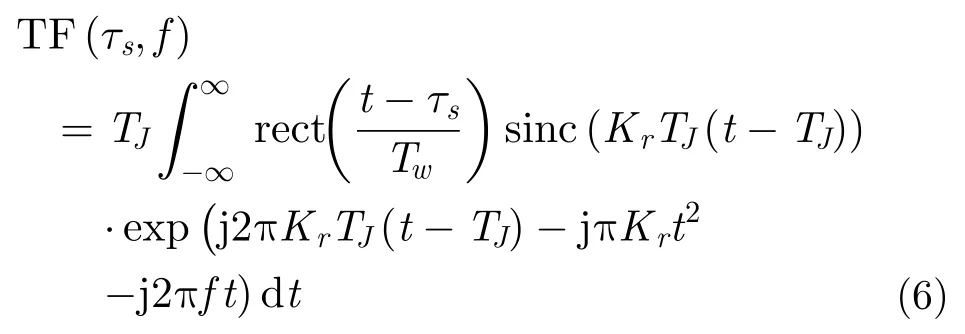
其中,τs為STFT的滑窗延時,Tw為滑窗寬度。
由于式(6)是一個Fresnel積分,不存在解析解,因此只能通過駐留相位定理給出近似結果。對該積分信號的相位進行求導并令導數為0,則可得時間與頻率的關系

將式(7)代入式(5),可得脈壓峰值附近的信號頻譜為

可得時頻分布的幅度響應為

式(9)表明,對于一個干擾切片的脈壓結果進行STFT,其在時域與頻域都表現為sinc函數;其時間維的主瓣寬度為ΔT=1/KrTJ,而頻率維的主瓣寬度則為ΔB=1/TJ。
對于間歇采樣直接轉發式干擾,其由多個延時相同的切片組成。經過脈沖壓縮后,在距離向僅存在1個假目標群;但是由于其截獲的不同切片具有不同的頻率分量,因此在頻率維表現為多個sinc函數。
在此基礎上,對每一個切片進行多次轉發,則構成了間歇采樣重復轉發式干擾。在這種干擾策略下,每一個假目標群都由多個延時相同的切片疊加而成;且不同的假目標群即對應于切片的多次轉發。則其時頻分布相當于對直接轉發式干擾的頻率維sinc函數在時域多次重復,進而形成時頻面上呈網格分布的多個峰值。
而對于間歇采樣循環轉發式干擾,根據圖1(c)所示工作原理可知:每個切片只有在進行第1次轉發時,才具有相同的延時,此后對于不同的干擾切片,其轉發延時都不相同。因此,其脈壓結果的時頻分布表現為時頻域上“雜亂”分布的峰值,對于不同的距離門,其頻域的sinc峰值個數不同。
根據以上特性,即可對間歇采樣轉發干擾的具體策略進行識別,設計的干擾策略辨識流程如圖2所示。其具體步驟如下:
(1) 對于接收信號依次進行脈沖壓縮和STFT處理;
(2) 基于時頻變換結果,分析每個距離門內的峰值個數Mp、 峰值的3 dB寬度ΔF以及存在峰值的距離門個數Np;
(3) 根據上述參數即可進行干擾辨識:
(a) 若峰值的3 dB寬度與發射信號脈寬近似相等,即ΔF≈Tp,則為目標回波(一般情況下,ISRJ的截獲時長小于脈寬的一半。因此只要ΔF>Tp/2即可認為為目標)。
(b) 若峰值的3 dB寬度小于發射信號脈沖寬度,即ΔF<Tp,且各距離門內峰值個數相等,則:
①Np=1時,為間歇采樣直接轉發式干擾;
②Np>1時,為間歇采樣重復轉發式干擾;
(c) 若峰值的3 dB寬度小于發射信號脈沖寬度,即ΔF<Tp,且各距離門內峰值個數不等,則為間歇采樣循環轉發式干擾。
需要說明的是:本文使用STFT進行時頻分析僅作為一個示例,STFT截斷窗的選取有可能導致時頻平面中峰值的分布規律發生變化,進而影響干擾辨識的效果。然而不同時頻分析方法的性能和參數選擇問題并不在本文討論的范圍之內,其具體內容可以參考相應領域的專業文獻[20]。
3.2 基于時頻域帶通濾波的干擾抑制
在干擾辨識的基礎上,可以確定目標與干擾各自所在距離門。則通過設計時頻域濾波器即可實現對干擾的抑制。假設經過干擾辨識后,可以確定目標所在距離門為r,則時頻域濾波器可以定義為
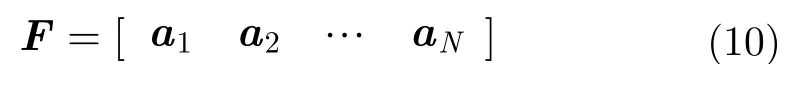
其中,N為時頻分布中時間維采樣點數(距離門的總數),i為時頻域濾波器在每個距離門的列向量,其定義為

利用該濾波器響應與脈壓結果的時頻分布相乘,即可對干擾進行抑制。濾波過程表明:對于目標所在距離門,其信號保持不變;對于干擾所在距離門,其濾波輸出等于該列最小值。若還需對脈壓結果進行后續處理(如相參積累等),則可對濾波輸出進行逆STFT,即可得到干擾抑制后的脈壓輸出。
4 仿真結果與分析
本節通過仿真對上述干擾辨識與干擾抑制算法進行驗證,并對算法性能進行分析。仿真中使用的部分參數如表1所示。
4.1 基于時頻分析的干擾辨識算法仿真

圖2 基于時頻分析的干擾辨識流程Fig.2 The flow of jamming recognition with time-frequency analysis
在干擾辨識仿真試驗中,定義信號類型變量s,其取值與信號類型的對應關系為:
(1)s=0,目標回波;
(2)s=1,間歇采樣直接轉發式干擾;
(3)s=2,間歇采樣重復轉發式干擾;
(4)s=3,間歇采樣循環轉發式干擾。
對于上述目標與干擾信號,其相應的脈沖壓縮結果與時頻分布分別如圖3和圖4所示。結合仿真結果與前文分析可知:目標與干擾在時頻域具有可分性,且不同干擾策略的時頻分布特征不同。基于該特征差異,可以進行干擾辨識。
其具體的仿真步驟如下:
(1) 對于一個固定的SNR(這里的信號泛指目標與干擾),任意生成一個0~4之間的整數,并根據前文對應關系生成雷達接收信號;
(2) 利用干擾辨識算法對接收信號進行處理,并記錄辨識結果:若辨識結果與信號類型相同,則記為一次正確辨識;
(3) 對上述過程進行1000次重復仿真,統計當前SNR下的正確識別率;
(4) 調整SNR,對上述步驟(1)-步驟(3)進行重復,得到不同SNR下的辨識算法性能曲線。
相應的仿真結果如圖5所示,可知當原始回波的SNR大于-3 dB時,正確辨識率可達90%以上。

表1 干擾辨識與抑制仿真參數Tab.1 Simulation parameters for jamming recognition and suppression
4.2 基于時頻域濾波的干擾抑制算法仿真
對于不同的干擾策略,其典型的干擾抑制效果仿真如圖6所示。在干擾抑制前,設置的信干比(Signal to Jamming Ratio, SJR)為-15 dB, SNR為-10 dB。經過脈沖壓縮處理后,SNR約為20 dB,而對于不同的干擾策略,峰值SJR約為-3~0 dB。從仿真結果中可以看出:對于不同的干擾策略,算法都可以有效地對干擾進行抑制;其獲得的信干噪比(Signal to Noise and Jamming Ratio, SJNR)改善約為18 dB。

圖3 目標與干擾的脈沖壓縮結果Fig.3 Pulse compression of target and jamming signal

圖4 目標與干擾脈壓結果的時頻分布Fig.4 The time-frequency distribution of pulse compression result of target and jamming signal
5 結束語
基于DRFM器件的間歇采樣轉發式干擾兼具壓制和欺騙2種干擾效果,其干擾參數靈活可變,對雷達探測構成了巨大威脅。本文對此類干擾的辨識與抑制方法進行了研究:基于脈壓結果的時頻分布,設計了干擾辨識流程;并通過仿真驗證了該辨識算法的性能,結果表明:在原始回波SNR大于-3 dB的條件下,正確辨識率可達90%以上。相對于已有算法,本文方法將干擾脈壓后的時頻分布特征總結為先驗知識,無需數據訓練即可直接進行干擾辨識。在此基礎上,提出一種基于時頻域濾波的干擾抑制算法,該算法可以在目標與干擾脈壓后距離可分的情況下,對不同策略的干擾進行有效抑制,其典型的信干噪比改善可達18 dB。
雖然本文研究僅針對單部ISRJ干擾機進行了討論,但是對于多部干擾機形成的多點源干擾環境,在干擾與目標脈壓后距離可分的前提下,本文方法仍然有效。基于脈沖壓縮波形的距離高分辨特性,結合現代雷達的自動檢測跟蹤功能,本文認為實際環境中干擾脈壓峰值長時間遮蔽目標峰值的概率非常小。
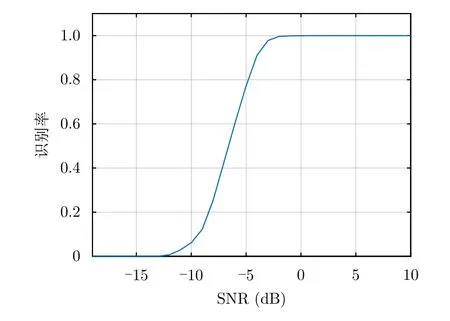
圖5 干擾辨識仿真結果Fig.5 Simulation results of jamming recognition
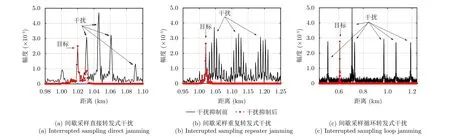
圖6 不同干擾策略下的干擾抑制結果Fig.6 Jamming suppression results of different jamming strategies

