基于灰色馬爾科夫模型的上海鐵路客運量預測

潘 麗，李 林 （上海理工大學 管理學院，上海 200093）

0 引言

隨著科學技術與經濟的不斷發展，社會的進步改變了人們的出行方式，鐵路客運速度的提高，載客量的龐大，使它成為了大多數人出行或旅游交通方式的選擇。因此為了方便人們更好的出行，對國家資源進行合理的配置，以及促進鐵路部門的發展，實現對鐵路客運量的預測變得越來越重要。為了把握鐵路運輸需求的特征，學者們提出了多種不同的預測模型，但是目前國內外常用的方法還是依賴大量的歷史數據，對其進行分析，找出規律，從而做出預測。

國外學者Suryani等建立了一個系統動力學框架模型來預測客運量需求，憑借系統動力學的物理特性和信息流反饋控制連續決策和行動，可以用來模擬、分析和仿真以提高模型的預測水平[1]。Godfrey等應用指數平滑法模型來對客運量進行預測[2]。相對來說，早期的研究方法比較單一，不能結合組合模型的優勢。

而國內學者研究客運量的人數更多，常用的預測方法有指數平滑法[3]、Logistic模型[4]、回歸分析[5]、支持向量機、神經網絡[6]等。這些預測方法具有各自的特點，但是有個共同的特點就是要求預測的歷史數據具有良好的平滑度。由于客運量受多種因素的影響，單一的預測方法已經不適合對波動性較大的客流量的預測，往往存在很多弊端。灰色馬爾科夫鏈模型是一種結合灰色系統理論和馬爾科夫鏈理論的預測模型，由于客運量具有明顯的灰度特征，因此可以使用灰色模型預測客運量。傳統的灰色模型雖然能有效地預測少量數據的序列，但隨著數據的增多和波動性的增大，該模型逐漸的失去了它的優勢[9]，而馬爾科夫模型預測適用于隨機波動性較大時間序列中，彌補灰色模型的不足[10]。因此，本研究將上述兩種模型相結合，使兩者優點互補。

1 建立灰色馬爾科夫模型

1.1 灰色GM （1,1）預測模型

灰色GM （1,1）模型是灰色系統理論最常用的一種灰色動態預測模型。是把觀測到的數據看作隨機時間變化的灰色量或灰色過程，通過累加生成或累減生成局部使灰色量白化，從而建立相應的微分方程模型并做出預測，其建模步驟如下：

（1）假設鐵路客運量原始序列為：

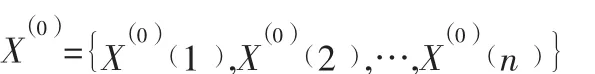
對原始數據進行一次累加得到：

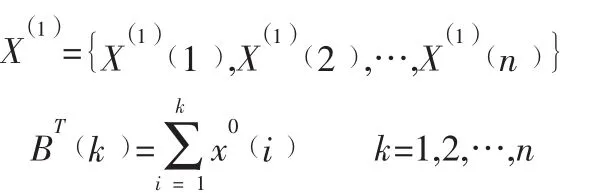
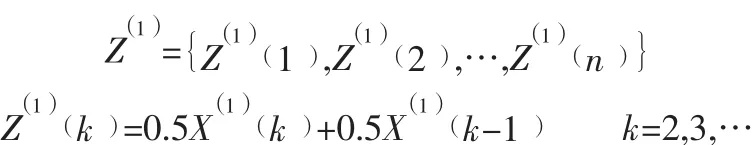
（3） 構建累加序列（X1）的一階微分方程：

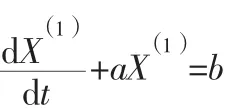
其中：參數a,b可由下列方程式得出：

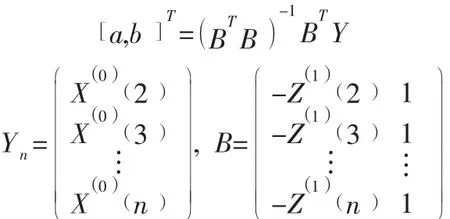
（4）求解微分方程，得到如下的GM （1,1）模型：

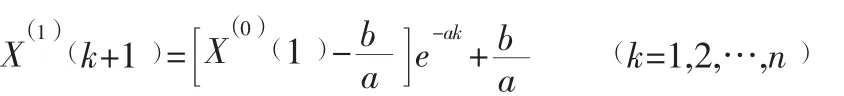
（5）由累加序列還原序列得到：

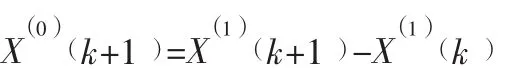
1.2 馬爾科夫模型

馬爾科夫模型是俄國數學家馬爾科夫于1907年提出，后有蒙特卡羅加以發展而建立的一種預測方法，它將時間序列看作一個隨機過程，通過對事物不同狀態的初始概率與狀態之間轉移概率的研究，確定事物未來狀態的變化趨勢。馬爾科夫模型可表示為：

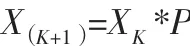
其中：X（K+1）,XK分別為在k+1、k時刻的狀態概率向量，P為一步狀態轉移矩陣。

（1）進行狀態區間的劃分

根據GM（ 1,1）模型預測的結果，計算原始序列與預測序列的相對誤差，并依據狀態的集中程度進行劃分。

（2）構建狀態轉移矩陣

由狀態Ei經過一個時期轉移到Ej的一步轉移概率為Pij，將所有的一步轉移概率排成一個矩陣，即：

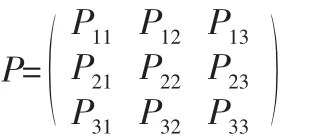
（3） 計算預測值

在狀態轉移矩陣確定后，根據某一年所處的狀態，來預測下一年可能出現的狀態，最終求出馬爾科夫修正值。

1.3 灰色馬爾科夫模型

灰色馬爾科夫模型的具體運算步驟：（1）選取預測的時間序列，構建GM （1,1） 模型，得到灰色預測值；（2）計算預測值與實際值之間的相對誤差；（3）根據相對誤差的大小，從而劃分誤差范圍；（4）計算狀態轉移矩陣；（5）對灰色預測值進行修正：

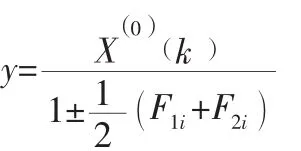
2 實證研究

通過收集資料，得到上海市2007~2016年的鐵路客運量數據，并利用灰色GM （1,1）模型求出預測值，再計算其真實值與預測值之間的誤差，以及相對誤差，得出的結果如表1所示：

2.1 用馬爾科夫鏈修正預測值

根據2007~2016年的上海鐵路客運量的實際值和相對誤差，劃分狀態區間，從表1可以看出相對誤差的最大值為6.63%，最小值為-5.79%，當灰色預測值與實際值相對準確時，不予修正。即誤差范圍在（-1%,1%） 之間時，將不對其進行修正，由此劃分三個狀態區間，分別為E1(-6,-2]，E2(-2,2]，E3(2,7]，如表2所示：

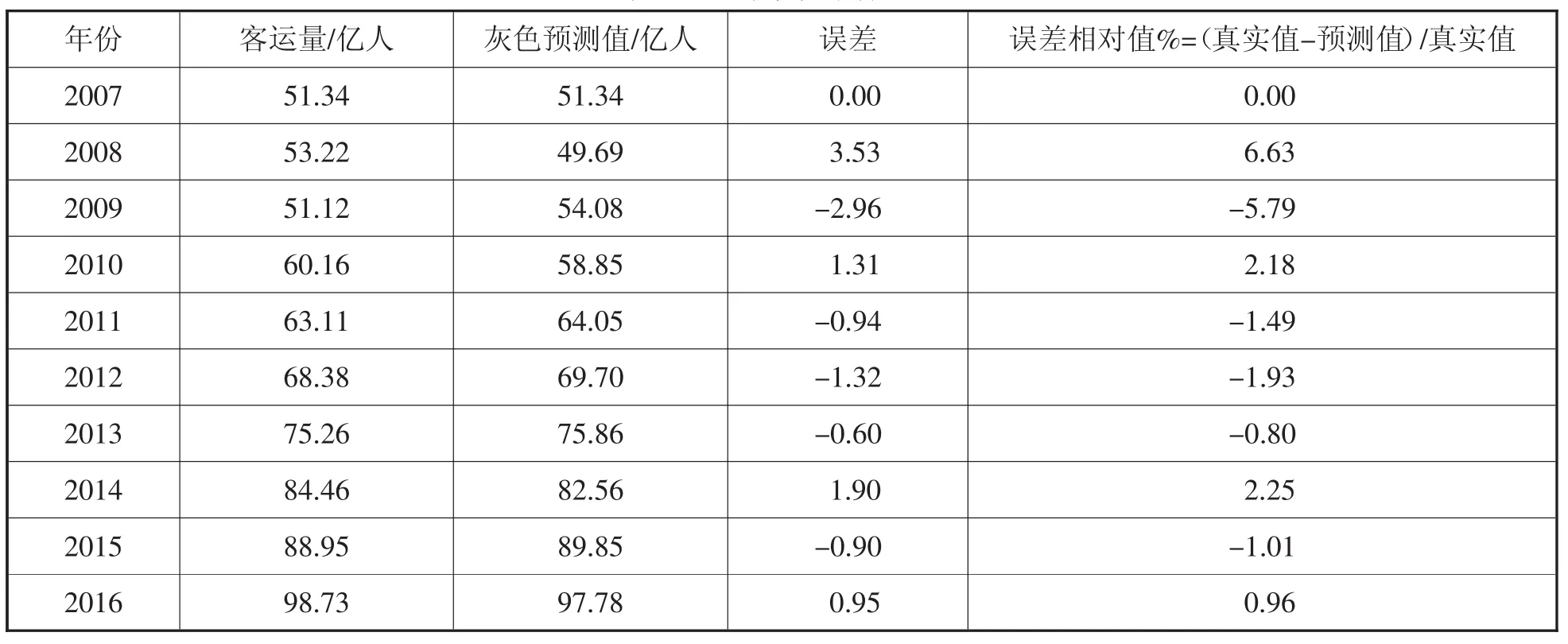
表1 上海市鐵路客運量

表2 狀態區間劃分

2.2 對各年進行狀態區間的劃分（如表3所示）

表3 相對誤差和狀態區間

2.3 構建狀態轉移矩陣

根據各年結果所在狀態區間，由狀態Ei經過一個時期轉移到Ej出現的次數除以Ei的次數，得到如下的一步狀態轉移矩陣和二步狀態轉移矩陣：

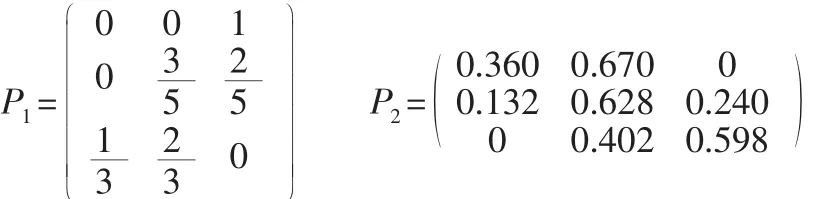
2.4 計算預測值

由狀態轉移矩陣及各年份所處的狀態，可以求出上海市鐵路客運量的馬爾科夫預測值。以2008年為例，則可以看出2007年的相對誤差處于E2狀態，經過一年的轉換，轉換為E2和E3的概率分別為3/5和2/5，則認為2008年的狀態最有可能處于E3狀態。運用GM （1,1）模型求得的2008年的預測值為49.69，則利用灰色馬爾科夫進行修正的預測值為50.60，運用同樣的方法得到的其他年份的預測值如表4所示：

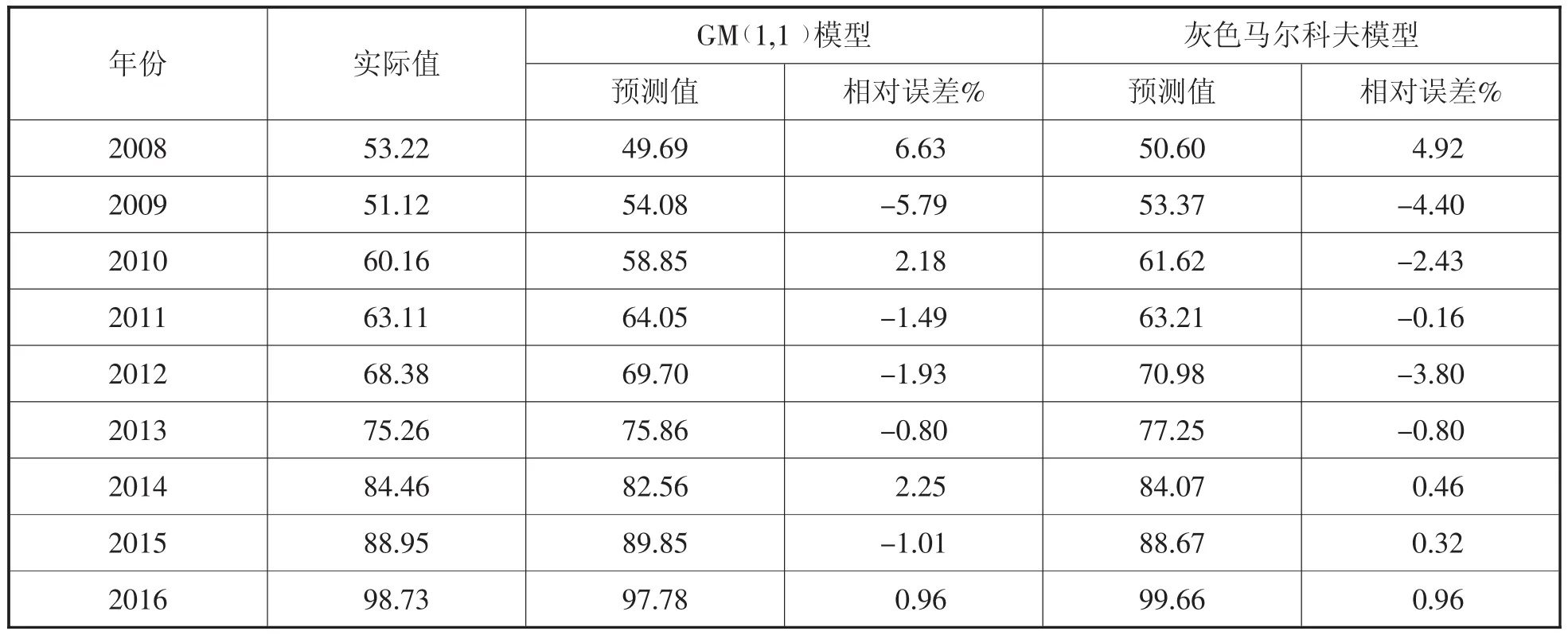
表4 灰色擬合值與馬爾科夫擬合值

從上述的預測結果可以得出：利用單獨的灰色模型求出的誤差是2.56%，利用灰色馬爾科夫模型求出的誤差是2.03%，對比兩種方法，降低了誤差范圍，說明灰色馬爾科夫模型的預測結果更好，更加適用于對客運量的預測。而且可以看出，灰色馬爾科夫預測值與實際值的擬合度較高，波動性一致，其參考價值高，利用灰色模型能看出哪些年份的預測值具有較大的變化趨勢，而從圖1中可以看出灰色模型是一條相對平滑的曲線。不能反映實際值的波動。

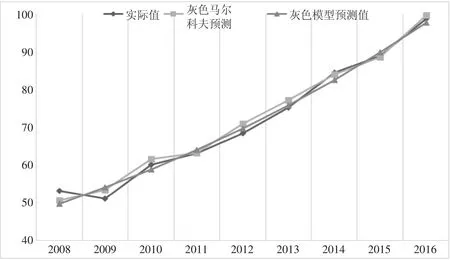
圖1 灰色馬爾科夫預測值與實際值和灰色值的對比曲線

2.5 由灰色馬爾科夫模型預測2017～2020上海客運量的預測值如表5所示：

表5 灰色馬爾科夫預測值

從預測的結果來看，上海鐵路客運量的增長是必然趨勢，趨于一種不穩定的螺旋式增長。鐵路部門自發展以來，以其獨特的優點吸引越來越多的乘客。本文利用灰色馬爾科夫模型，充分考慮了鐵路客運量的增長趨勢和隨機變動趨勢，并將兩個方面加以考慮，使預測效果更加具有可信性，通過合理利用可以對鐵路客運決策產生積極影響。

3 結論

為提高客運量準確性，把握客運量發展趨勢，從而更好地幫助鐵路行業和相關企業的決策提供科學依據。無論是在鐵路還是公路等方面，客運量的預測都是非常重要的手段，在信息發展迅速的今天，客運量的預測能夠為相關的部門提供合理地決策依據和建議。

（1）灰色馬爾科夫在上述各列表的相對誤差的絕對平均值都小于5%，預測結果精確度較高，且效果比灰色預測法更加穩定。

（2）對于實際值序列模型改變明顯時，組合預測法的結果優于單一預測法結果，從表4可以明顯看出，灰色馬爾科夫模型一方面吸收了灰色預測法的有效信息，另一方面也利用了馬爾科夫模型的優勢，降低了數據的隨機性。

（3）但是灰色模型作為一種理論的預測方法，其結果未考慮到客運量變化的主要影響因素。實際情況遠遠比模型更加復雜，其結果往往起參考作用。通過進一步結合馬爾科夫模型，提高精確度。