基于加權K-Means和局部BPNN的票房預測模型①

米傳民,魯 月,林清同

1(南京航空航天大學 經濟與管理學院,南京 211106)

2(大葉大學 資訊管理學系,彰化 51591)

電影作為很典型的短周期體驗型產品,其票房收益受到很多因素的共同影響且其影響機制較為復雜,因此對其票房進行預測是較為困難的.據統計,目前我國國產電影目前只有少數電影投資是盈利的,大部分國產電影基本都難以回收成本的.在這一背景下,對電影票房進行預測無疑對風險控制、充分調動投資者的積極性以及扭轉目前的發展局勢具有巨大的現實意義.本文主要構建一種基于加權K-均值以及局部BP神經網絡的票房預測模型對目前的票房預測模型存在的不足進行改進,從而提高票房預測的精度.

目前關于票房的研究主要分為兩個研究方向: 票房影響因素的研究以及票房預測模型構建方面的研究.傳統的票房影響因素研究主要是針對票房靜態影響因素的研究,這些因素在電影上映之前就已經確定且不會隨著時間的變化而變化.聶鴻迪等人[1]選取檔期、電影類型以及主創陣容等因素進行研究.羅曉芃等人[2]添加續集這一因素探究其對票房的影響.鄭堅等人[3]將演員、導演、地區、類型等量化成連續數值來提高預測準確度.韓明忠[4]、劉濤[5]也做了類似的研究.除此之外,隨著互聯網的興起,在線評論、網絡搜索等動態影響因素借助于網絡的放大效應,逐漸成為了票房的重要影響因素,因此,越來越多的研究者將這些動態因素加入到票房預測模中: 王煉等人[6]引入網絡搜索量進行研究.郝媛媛[7]、丘萍等人[8]通過對在線電影平臺網絡口碑數據進行分析得出網絡口碑對票房收益有顯著影響.Lee JH[9]等人引入熵的概念來衡量評論整體的可信度對票房的影響.袁海霞[10]引入信息熵對網絡口碑跨平臺分布特征進行量化驗證其與產品銷量之間的關系.

票房預測模型構建方面的研究主要涉及預測方法、樣本處理、模型構建過程等方面.票房預測中應用較多的預測方法主要有線性回歸以及機器學習等方法: 李特曼、斯格特·蘇凱的模型都是經典的線性回歸模型[1].部分學者研究了線性回歸以及機器學習方法哪種方法更適用于票房預測: 聶鴻迪[1]、Du J[11]、Hur M等人[12]主要運用線性回歸與SVM、ANN、CART、SVR等方法對票房進行預測,得出機器學習優于線性回歸的結論,表明機器學習方法更適用于電影這種短周期體驗型產品的預測.Kim T[13]等人將三種機器學習方法得到的結果進行平均,結果優于單一的機器學習方法.韓忠明等人[4]對特征與電影票房建立GBRT模型,對票房進行預測.因此,目前進行票房預測的首選方法主要是機器學習方法: 魏明強[14]利用神經網絡方法分析了網絡評價在不同時段對票房走勢的影響.劉濤[5]分別采用SVM以及ANN對票房進行分類預測,結果證明ANN的預測效果優于SVM.因此目前大部分學者對票房進行預測時都會選擇神經網絡相關方法,其中最為常用的是BP神經網絡: 鄭堅[3]、 Zhang L[15]分別構建了基于多層BP神經網絡的票房預測模型對票房進行預測.除此之外還有部分學者對預測模型構建過程的其他方面進行改進: Hur M[12]考慮到電影上映的不同時段影響票房的因素側重點會有所變化,分別構建了六個票房預測模型來提高預測的準確度.李金芝[16]在構建票房預測模型中應用靈敏度分析確定各參數對模型輸出結果的影響力大小,對輸入變量進行篩選.

通過對電影票房預測相關研究的總結可以得出,在票房影響因素方面雖然目前很多已經將網絡口碑相關信息加入到了預測模型中,但大部分研究僅僅考慮了單一平臺,并沒有深入考慮到網絡口碑的跨平臺分布特征,并且針對單一平臺的網絡口碑影響力研究并不能很全面的反映網絡口碑對票房的影響;在預測模型構建方面,目前大多數學者都選擇基于神經網絡的預測方法,另外還有一些學者對票房預測模型的構建過程進行優化,但大部分研究者都用整體樣本對模型進行訓練.在此情況下,很難有一個預測模型能對如此復雜現實票房進行很好的擬合.因此有的研究者在對模型進行訓練之前對樣本數據進行分類,但目前的主要是應用簡單的K-均值聚類,在聚類過程中不同的影響因素被賦予同等的權重,而實際情況中,不同的影響因素影響力是不同的,因此簡單的K-均值聚類雖然在一定程度上提高了訓練集的質量,但是由于沒有考慮到不同因素的影響力問題,會在一定程度上影響最終預測結果.

基于上述的問題,本文構建了一種基于加權K-均值聚類和局部BP神經網絡的票房預測模型: ① 構建基于隨機森林的影響因素影響力測量模型,并以此為依據對票房影響因素進行篩選,以此來簡化后續預測模型的輸入;② 考慮到不同影響因素對票房的影響力不同的現實情況,為了解決以往研究中對影響因素權重平均分配的問題,構建了基于加權K-均值和局部BP神經網絡的票房預測模型,以因素影響力為依據對樣本數據進行加權的K-均值聚類,并基于子樣本構建局部BP神經網絡模型進行票房預測.

1 理論方法

1.1 隨機森林

隨機森林(Random Forest,RF)[17]是一種由多個獨立的決策樹組合而成的集成分類器.其決策原理可以描述為[18]: 若干個專家聚集在一起對某個特定的任務進行分析并根據自身“經驗”給出自己認定的正確結果,最后隨機森林通過專家投票的方法,采用“少數服從多數”的原則得出最后分類結果.其生成過程主要可以分為以下幾個步驟:

Step 1.通過Bootstrap方法從整體的訓練集數據中隨機抽取,生成k個子樣本集,以及k個袋外數據;

Step 2.根據隨機抽取生成的k個子樣本集,依據構建決策樹的原理及方法選擇合適的節點分裂算法來構建k棵相互獨立的決策樹;

Step 3.將Step 2中生成的k棵決策樹進行集成,構建隨機森林集成分類器;

Step 4.將測試集輸入到隨機森林分類器中,利用Step 3構建的隨機森林分類器對其進行分類.

1.2 加權K-均值聚類

K-均值算法是一種很有代表性的基于距離的聚類方法,它將距離作為評價樣本之間相似性的依據,即越近的兩個對象其類似度越大.假設有n個樣本且每個樣本包含m個屬性,形成了一個包含n個m維數據點的樣本數據集,則聚類過程主要可以概括為以下幾個步驟:

Step 1.選取k個樣本點作為初始聚類中心(質心);

Step 2.計算每個樣本與各質心的距離,并將其指派到距離最近的質心,完成一次迭代;

Step 3.對每個分組內的質心進行更新;

Step 4.判斷是否滿足算法終止條件(質心不變/距離平方和最小): 若滿足則聚類完成;否則,重復Step 2～Step 3直到滿足終止條件.

在上述K-均值聚類算法中,樣本的每個屬性被賦予了同等權重1 /m,若對不同屬性賦予不同的權重,即加權K-均值聚類.簡單來講,加權K-均值聚類在計算樣本點到質心的距離時,用各個屬性對應的權重替代原來的等權權重1 /m,加權K-均值聚類算法中第i個樣本點到質心的距離計算公式為公式(1)[19]:

1.3 BP神經網絡

在多種神經網絡模型中,多層前向神經網絡由于其成熟的算法,較強的非線性映射能力、泛化能力以及容錯能力成為了應用最為廣泛一類神經網絡模型,其中最為典型的算法為誤差反向傳播算法—BP(Back-Propagation)算法,BP算法對應的模型即為BP神經網絡模型,BP神經網絡是一種典型的信號單向傳播的多層前向神經網絡.BP神經網絡的訓練過程主要包括兩個部分: 信號的正向傳播、誤差的反向傳播.在正向傳播過程中,信號由輸入層經過隱含層到輸出層生成輸出結果與期望輸出進行對比,若結果不理想則啟用誤差的反向傳播過程,誤差信息將由輸出端開始逐層進行反向傳播從而對網絡中的權值進行調節,從而使得信號正向傳播過程中得到的輸出結果更接近理想輸出.

2 基于隨機森林的重要票房影響因素篩選

2.1 影響因素量化

2.1.1 電影類型

結合較為權威的電影類型分類以及我國國產電影類型的發展現狀在本文的電影類型中主要包含劇情、愛情、喜劇、動作、驚悚、奇幻、懸疑其中類型.在對類型變量進行量化時,主要借助于各個類型的歷史票房數據對其影響力進行衡量,其求解公式如下:

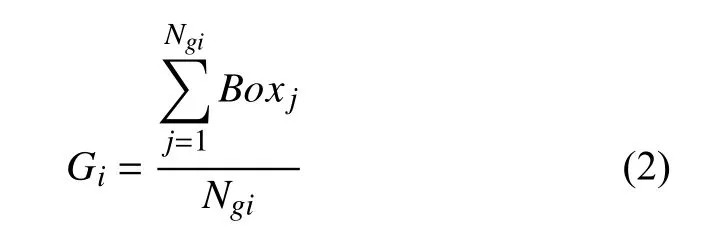
其中,Gi表示第i個 電影類型的影響力,Ngi代表的是在所收集的樣本中屬于第i個類型的電影數量,Boxj表示第j個屬于第i個類型的電影的票房.本文主要考慮電影的第一類型和第二類型.

2.1.2 演員

考慮到名品演員影響力的持久性以及人氣偶像演員的瞬時性,本文在對演員影響力進行量化時主要從兩個方面進行,一方面從演員的歷史參演電影的平均票房入手衡量其持久影響力,另一方面借助于百度搜索這一平臺提取電影上映時相關演員的平均搜索量—網絡搜索量(network search volume)來衡量其瞬時影響力.其求解公式為:

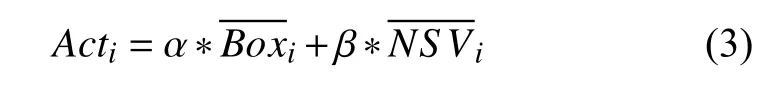
其中,Acti表 示第i個 演員的影響力,α和 β 表示歷史票房以及網絡搜索量的重要性系數,表示該演員近期內作為主演參演電影的平均票房,表示在電影上映時該演員的平均網絡搜索量.一般情況下一部電影會有很多個演員參演,在此我們只考慮第一主演和第二主演.

2.1.3 導演

在對導演影響力進行量化時不僅要考慮到其作為導演身份的影響力還要考慮到其本身具有的其他身份的影響力,本文主要通過該導演作為導演參與的電影票房以及作為演員參與的電影票房、其他身份的影響力主要通過網絡搜索量來衡量,因此導演影響力的求解公式為:

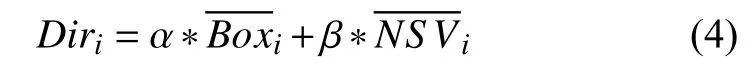
其中,Diri表示第i個 導演的影響力,α和 β 表示歷史票房以及網絡搜索量的重要性系數,表示其作為導演以及其作為主演參演電影的平均票房,表示在電影上映時該導演的平均網絡搜索量.

2.1.4 檔期

本文在對前人對電影檔期研究做了充分總結的基礎之上,最終將電影檔期分為以下幾種: 賀歲檔(前一年的11月底至下一年的二月底)、五一檔(每一年的4月底到5.3)、暑期檔(每一年的6月初到8.31)、十一檔(每一年的9月底到10.7).本文在對檔期變量進行量化時,借助于往年各個檔期的票房數據對檔期影響力進行衡量,其求解公式如下:

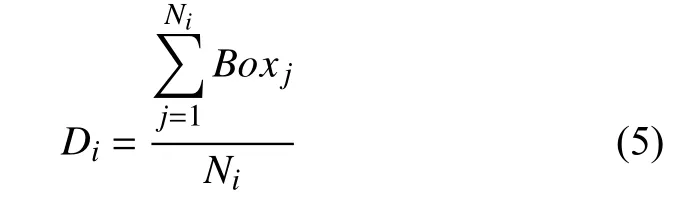
其中,Di表示第i個 檔期的影響力,Ni代 表的是第i個檔期所包含的天數,Boxj表 示在第i個 檔期內的第j天所有電影所產生的總票房.

2.1.5 網絡搜索量

一部電影在上映期間對應的網絡搜索量從一個側面反映了潛在觀影者對其的關注度,雖然不同的潛在觀影者會在搜索之后做出不同的觀影決策,但是從另一個層面來講,越多的人關注就表明可能有更多的潛在觀影者會選擇去觀看這部電影,因此本文將網絡搜索量作為一個潛在觀影者對電影的關注度的衡量指標,由于百度是目前國內用戶基礎最大的搜索引擎,其搜索數據具有較強的代表性,因此本文變量網絡搜索量Searchi具體量化數據來自百度搜索指數.

2.1.6 網絡口碑數量與效價

考慮到現實情況中一般潛在觀影者不會在單一平臺搜集信息之后就馬上作出觀影決策,而是通過多個平臺搜索之后經過對比衡量之后最后才作出觀影決策,所以本文在對網絡口碑數量以及效價進行量化時采用多平臺評論數量求平均值的方法,并且考慮到不同平臺之間的用戶基數以及評分機制的不同,本文在對口碑數量以及口碑效價進行平均之前,首先對其進行歸一化,最終得到網絡口碑數量變量值Amounti以及網絡口碑效價的量化結果Ranti.

2.1.7 網絡口碑離散度

網絡口碑離散度指的是網絡口碑在不同平臺之間的傳播程度,即: 網絡口碑的跨平臺分布特征.為了更為全面的對網絡口碑的跨平臺分布特征進行量化,本文從口碑數量和口碑效價兩個方面進行探究: 引入信息熵(information entropy)這一概念,構造數量信息熵(IE_Voli)以及效價信息熵(IE_Vali)對口碑離散度進行量化.信息熵是信息論中用于測算所有可能發生情況的平均不確定性的指標,信息熵越大,說明整體系統越混亂,即各個事件發生的概率分布越平均.本文在對網絡口碑離散度進行量化時主要思路是將信息熵求解公式中的事件發生的概率替換為網絡口碑各個特征值,并通過公式(6)和公式(7)進行求解:其中,j代表第j個電影網絡口碑平臺,Total_Voli代表第i部電影在各個平臺的評論數的總和,Total_Vali代表第i部電影在各個平臺的總評分的總和.代表第i部電影在第j個電影網絡口碑平臺的網絡口碑數量特征值,代表第i部 電影在第j個電影網絡口碑平臺的網絡口碑效價特征值.

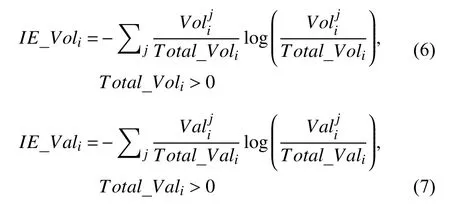
2.2 基于隨機森林的因素影響力判定和指標篩選

2.2.1 基于重要性分數的因素影響力

利用隨機森林算法對變量重要性進行判定時主要采用變量重要性分數(variable importance score),其主要作用是對各個條件屬性對于決策屬性的影響程度進行衡量.本文主要采用基于置換的變量重要性分數.將整體訓練樣本集的集合設為D,并且將用向量Xj,j=f1,2,···,11g表示影響電影票房的因素,對整體訓練樣本采用Bootstrap抽樣生成K個子訓練樣本集,則第k個樣本子集則表示為Dk,則變量重要性分數則表示為向量VIS=fVIS1,VIS2,···,VISj,···,VIS11g,則通過變量重要性分數對票房影響因素進行衡量可以總結為以下幾個步驟:

Step 1.首先將k值取1;

Step 2.并在其對應的子訓練集Dk的基礎上構建決策樹Tk,同時將對應的袋外數據用表示;

Step 3.應用Step 2中生成的決策樹Tk對對應的袋外數據進行分類,并計算其分類準確率;

Step 4.對于變量Xj,j=f1,2,···,11g,對其變量值進行變換直至其原始袋外數據樣本自變量與因變量之間的關系被打斷,并將針對該變量擾動之后的袋外數據用表示;

Step 5.應用Step 2中生成的決策樹Tk對擾動后的袋外數據進行分類,并計算其分類準確率;

Step 6.分別另k=1,2,···,K,對其重復進行Step 2～Step 5的操作,得出各個子訓練集對應下的擾動前后的分類正確率;

Step 7.通過公式計算特征Xj的變量重要性分數,其求解公式為式(8):

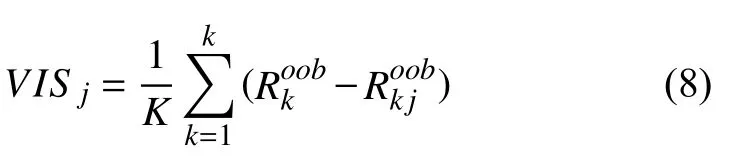
Step 8.對j=f1,2,···,11g重復上述過程,得出所有變量重要性分數,輸出重要性分數向量VIS=fVIS1,VIS2,···,VISj,···,VIS11g.

通過對樣本數據集進行上述操作得到票房影響因素的重要性分數,可以看出,當對一個變量的對應值進行變換前后分類準確率減少量越大,表明這一變量重要程度越強,反之則表明該變量不是很重要,因此對其變量值進行擾動不會對最終分類結果造成影響.

2.2.2 票房影響因素篩選

通過構造隨機森林并通過隨機森林的重要性分數對影響電影票房的各個影響因素的重要性進行衡量,并以各個變量的重要性分數作為其對票房重要性的依據,從而對各個影響因素的重要性進行比較,進行指標篩選,從中選出重要性較高的票房影響因素用于后續票房預測任務.但是由于隨機森林的特性,當依據樣本數據對票房影響因素的重要性分數進行求解時,同樣的數據在多次試驗中得出的各個因素的重要性分數是不同的,但是觀察多次試驗的結果可以看出,每個影響因素的重要性分數的值都在一定的范圍內波動,因此本文在對因素重要性進行衡量時,采取多次試驗求平均值的方法.

3 基于加權K-均值和局部BP神經網絡的票房預測

3.1 基于加權K-均值的訓練數據分類模型

簡化后的指標體系中各個票房影響因素的個數為n,j代表第j個影響因素,則wj則 表示第j個影響因素的權重,最佳聚類數用k表示,另外i表 示第i個電影樣本數據.則加權K-均值聚類算法中第i個樣本點到質心的加權歐式距離EDi計算公式為式(9):

基于加權K-均值的樣本分類可以分為以下步驟:

Step 1.隨機選取k個樣本點作為初始聚類中心(質心);

Step 2.依據式(9)計算其余每個樣本與各個質心的加權歐式距離,并將其指派到距離最近的質心,完成一次迭代;

Step 3.對每個分組內的質心進行更新;

Step 4.判斷是否滿足算法終止條件: 滿足的話,聚類完成;否則,重復Step 2～Step 3直到滿足終止條件,完成聚類.

通過對樣本數據進行加權K-均值聚類,對不同影響因素賦予不同的權重,彌補了一般K-均值聚類中各因素權重平均分配忽略不同影響因素影響力之間差異的問題,因此,在考慮到不同影響因素對電影票房影響力的差異的基礎上對樣本數據進行分類可以使得最終的分類結果更為科學.

3.2 基于BP神經網絡的票房預測模型

3.2.1 BP神經網絡結構設計

BP神經網絡的結構設計主要包含網絡層數確定、輸入層和輸出層設計以及隱含層設計三個方面:根據Kosmogorov定理,在合理的條件下,一個三層BP神經網絡可以擬合出任意復雜的連續函數.因此本文所構建的BP神經網絡為三層神經網絡(如圖1);輸入層以及輸出層所包含的節點數主要由數據本身特征所決定,輸入層的節點數為自變量的數目,輸出層的節點數為目標因變量的數目.因此本文所構建的BP神經網絡預測模型中,輸入層節點數目為簡化后對應的影響電影票房的因素的個數.輸出層節點只有一個,代表票房變量;隱含層設計的主要是確定隱含層所包含神經元的數目,其確定公式為公式(10),其中nh代表隱含層神經元的數目,ni表示輸入層神經元的數目,no表示輸出層神經元的數目,a為認為設定的可變常數并且a2[1,10].

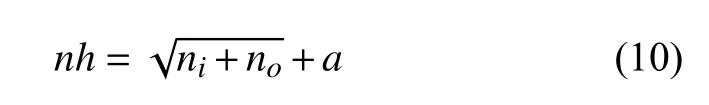
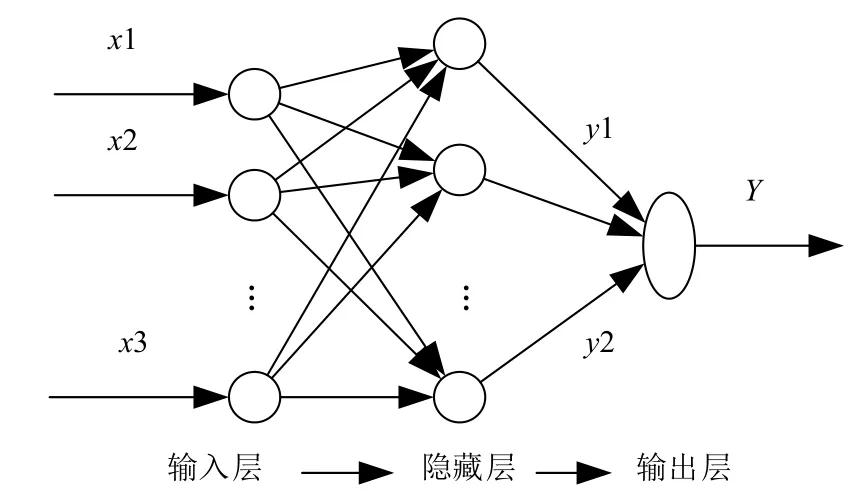
圖1 三層BP神經網絡結構圖

3.2.2 BP神經網絡參數選取

BP神經網絡的參數選取主要包含初始權值及閾值選取、學習速率的選取、激活函數以及學習函數的選擇三個方面: 在對初始權值以及閾值進行確定時,本文選擇采用隨機生成初始權值及閾值的方法;學習速率η 的值通過BP神經網絡在訓練過程中權值的修正量來影響神經網絡的學習過程.通過對相關理論以及文獻的學習以及總結,常用的學習速率的取值范圍在0.01到0.8之間.常用的激活函數有單/雙極性Sigmoid函數、正弦函數等.本文在進行BP神經網絡建模時選擇單極性Sigmoid函數,其數學表達式如公式(11):

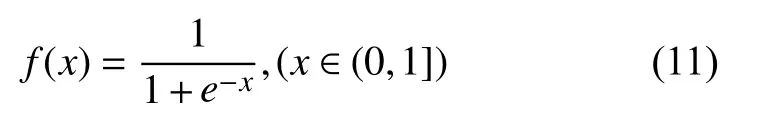
目前常用的學習函數有: 動量BP算法、擬牛頓法及L-M算法等等.同時L-M算法由于其具有較高的學習速率以及較快的收斂速度最為常用,因此本文在進行BP神經網絡建模時也選擇L-M算法作為學習函數.

3.2.3 BP神經網絡模型構建

通過前文的BP神經網絡結構設計以及BP神經網絡的主要參數選取,確定了本文BP神經網絡模型的基本結構,在對本文BP神經網路進行建模以及訓練時主要流程以及思路如圖2所示.

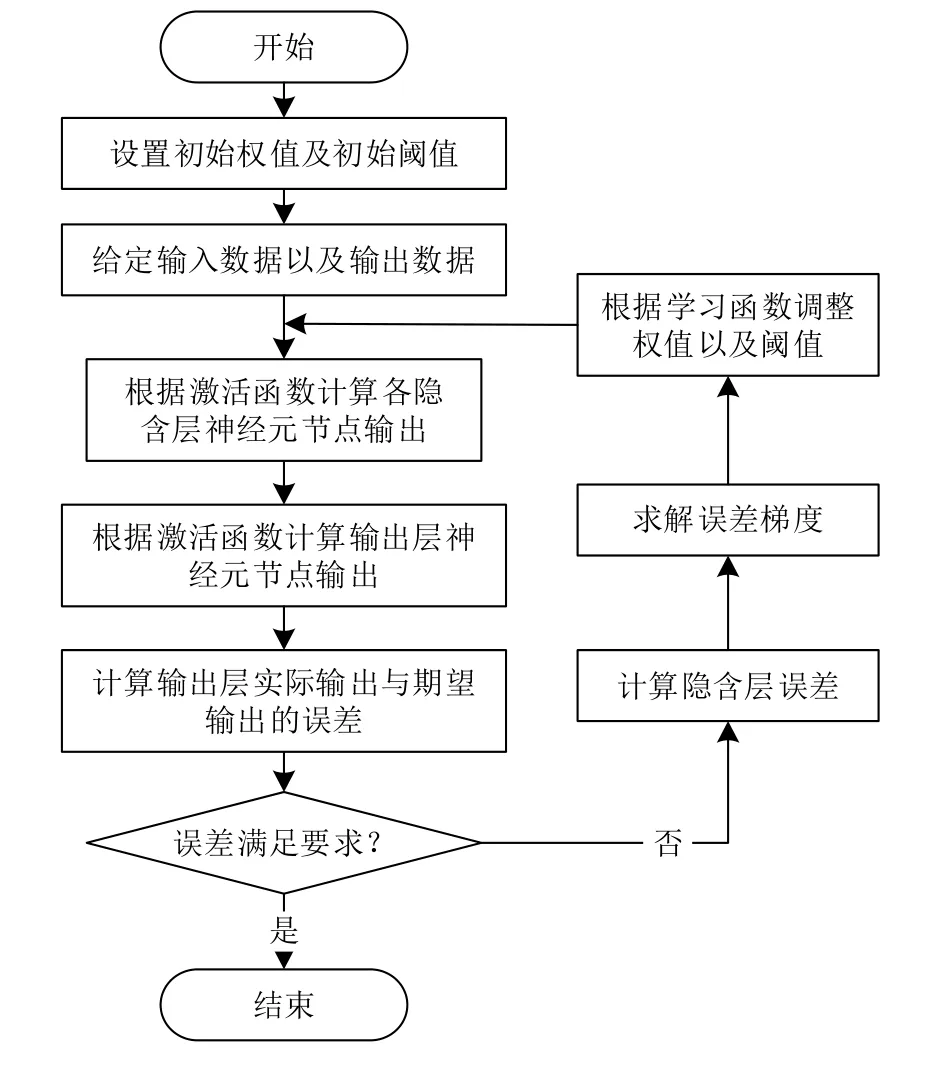
圖2 BP神經網絡模型流程圖

3.3 基于局部BP神經網絡的票房預測模型構建

基于加權K-均值聚類的局部BP神經網絡票房預測模型的主要思路為: 通過加權K-均值聚類將原始樣本數據分為若干個樣本子集,并基于各個樣本子集構建對應的局部BP神經網絡票房預測模型,并且對新的電影數據進行票房預測時,通過判斷其與各個樣本子集的聚類中心的加權歐式距離來決定調用哪一個局部BP神經網絡對其進行預測,并在這一過程中加入判斷條件,來決定是否要將新數據加入樣本子集中;另外隨著新數據的加入,整體樣本的分類效果可能在某一時刻不再是最佳分類,所以在過程中加入了整體數據分類效果的判定,決定是否需要對整體樣本數據重新進行分類.具體可以分為以下幾個步驟(如圖3所示).

Step 1.初始化參數: 加權歐氏距離臨界值ED;

Step 2.對數據集內的所有數據進行加權K-均值聚類,得到若干個樣本子集以及各樣本子集的聚類中心;

Step 3.對這若干個樣本子集構建對應的局部BP神經網絡票房預測模型,使得樣本子集、樣本子集聚類中心、局部BP神經網絡預測模型一一對應;

Step 4.輸入待預測數據,計算其與各個樣本子集聚類中心的加權歐氏距離,并選擇距離最小的對應局部BP神經網絡模型對其進行預測,得到預測結果;

Step 5.判斷該條數據與最近聚類中心的加權歐氏距離是否小于設定的加權歐氏距離臨界值ED,若在臨界值內則將該條數據加入該樣本子集,轉Step 3,否則舍 棄該條數據,轉Step 4.

4 實驗驗證

4.1 數據來源與量化

4.1.1 數據來源

本文樣本主要包含2016-2017年間的電影數據,主要來源于藝恩咨詢、百度指數、豆瓣網、時光網以及貓眼電影等平臺.其中票房、類型、演員、導演、檔期等數據來源于藝恩咨詢.網絡搜索量相關數據來自于百度指數.網絡口碑相關信息從豆瓣網、時光網、貓眼電影收集得到.本文收集到的原始數據共包含415部國產電影,在此基礎之上,剔除數據不全、票房過低以及特殊題材的電影后用于實證分析的電影數據共有327部.

4.1.2 樣本數據量化

在對樣本數據進行量化時,考慮到不同的變量量化之后具有不同的量級,不同量級的數值可能會對接下來的影響因素重要性判斷造成影響,本文通過歸一化數據來去除數據的不同量級對因素重要性判別的影響,進一步歸一化之后的數據描述性統計如表1所示.

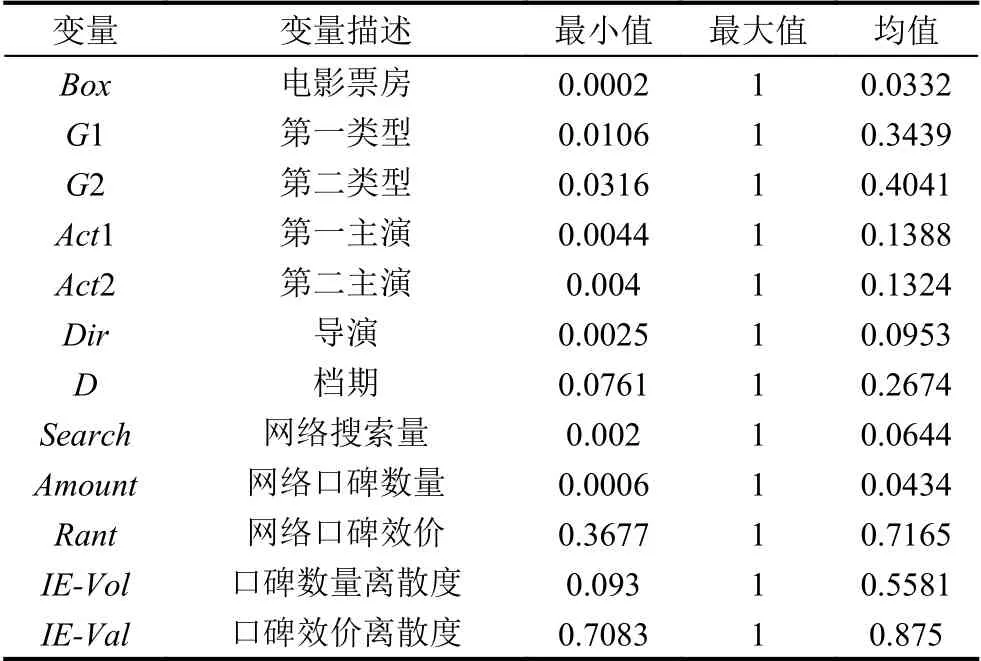
表1 歸一化數據描述性統計分析表

4.2 基于隨機森林的重要票房影響因素篩選

根據前文介紹的基于隨機森林的票房影響因素變量重要性分數的求解過程對各個變量的重要性進行求解,由于隨機森林的算法特性導致在利用隨機森林算法進行變量重要性分數求解時其結果會具有一定的波動性,因此本文在進行實驗時采用多次建模求平均值的方法對變量重要性進行判定,最終求解結果如圖4所示.

通過對結果的觀察可以看出在所有的影響因素中,網絡搜索量的對應的重要性分數最高,說明在影響票房的所有因素中,這一因素發揮的作用最大,其次是網絡口碑數量、口碑數量離散度等影響因素,另外通過對圖4中變量重要性分數分布結果圖的觀察可以看出,有部分影響因素的重要性分數很小幾乎接近于零,表明這些因素在對票房的影響方面發揮的作用很小,相對于其他的重要性分數較大的因素其作用幾乎可以忽略不計,這些因素包括: 口碑效價離散度、口碑效價以及第二類型,因此為了簡化后續的票房預測模型輸入,本文在進行票房影響因素的選擇時只選取影響力較大的因素,去掉一些作用很小的影響因素,從而在輸入層對預測模型進行簡化.因此,篩選后的票房影響因素共包含網絡搜索量、口碑數量、口碑數量離散度、第一主演、第一類型、第二主演、導演和檔期等因素.

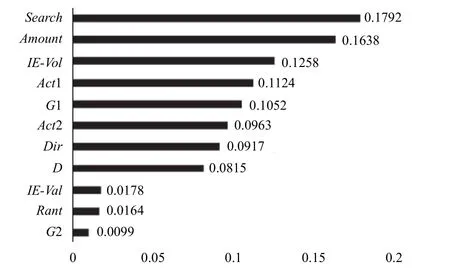
圖4 變量重要性分數結果圖

4.3 基于加權K-均值和局部BP神經網絡的票房預測

通過對篩選后的影響因素的變量重要性分數進行歸一化處理得到各個影響因素的對應權重,影響因素及其對應權重結果如表2所示.

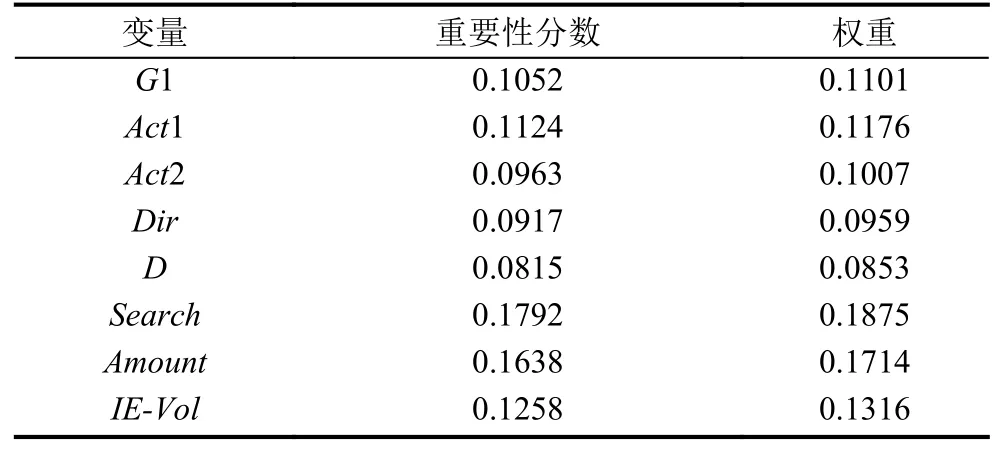
表2 影響因素及其權重結果表

在對最優聚類數進行確定時本文所采用的方法為:通過對每個聚類數對應的F值(組間離差平方和的平均值除以組內離差平方和的平均值)進行比較,當聚類數發生變化而跟其相對應F值不變化或者變化很小的話,對應的聚類數即為最佳聚類數.通過計算得出電影樣本數據分類的最佳聚類數為3,通過加權K-均值聚類將電影樣本數據分為3類,分別以三類子樣本為依據構建局部BP神經網絡模型,本文采用Python編程來實現BP神經網絡預測的功能,其中部分參數設置如表3所示.

表3 BP神經網絡參數設置

為了對本文構建模型的效果進一步進行驗證,本文同時設置了對比實驗,在對比實驗中首先采用簡單K-均值聚類對樣本數據進行聚類,并在此基礎上構建BP神經網絡進行票房預測,同樣采用Python編程實現,從而對本文的改進效果進行驗證.

4.4 結果對比及分析

平均絕對百分比誤差(Mean Absolute Percentage Error,MAPE)是對預測模型進行評估時常用的一種指標,其值可以通過公式(12)求得,其中Vpi表示第i個樣本的票房預測值(Predictive Value),Vai表 示第i個樣本的實際票房值(Actual Value),n表示用于預測實驗的樣本數.

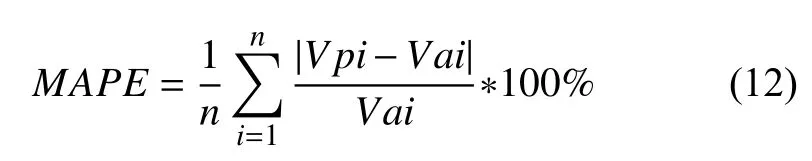
在采用兩種模型進行預測時,由于受BP神經網絡模型自身特征影響,其預測結果會在一個特定范圍內產生一定的波動,因此本文在對兩個模型的預測效果進行衡量時,采用多次預測求平均值的方式,實驗結果如表4所示,最后得出基于本文構建的模型進行的票房預測的平均絕對百分比誤差(MAPE)控制在8.49%,對比模型平均絕對百分比誤差(MAPE)控制在10.39%.可以看出本文構建的基于加權K-均值以及局部BP神經網絡的票房預測模型的預測結果要優于對比模型的預測結果,從而證明了本文所構建的票房預測效果.

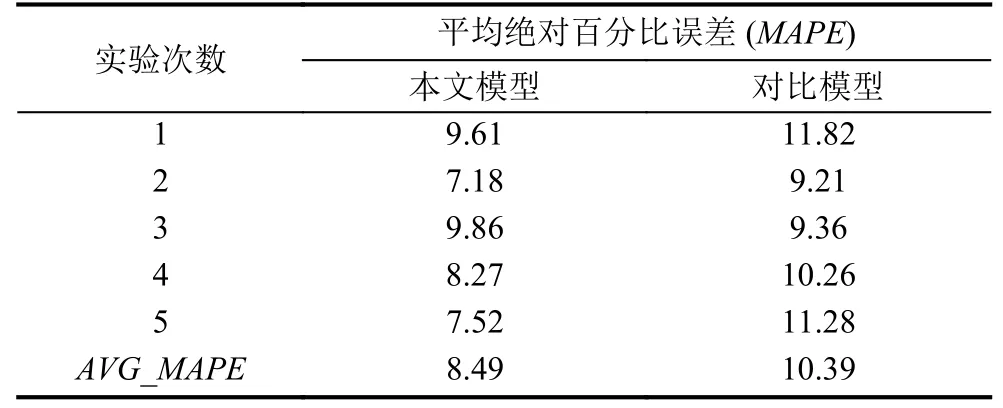
表4 兩模型預測效果對比表(%)

5 總結與展望

電影作為很典型的短周期體驗型產品,其票房收益受到很多因素的共同影響且其影響機制較為復雜,因此對其票房進行預測是較為困難的.本文在對電影票房預測研究進行了較為全面的總結與分析的基礎上,對電影票房預測建模過程進行了一定的優化與改進,構建了基于加權K-均值聚類以及局部BP神經網絡的票房預測模型,本文的研究可以總結為以下幾個方面:

(1)構建基于隨機森林的影響因素影響力測量模型,并以此為依據對票房影響因素進行篩選,以此來簡化后續預測模型的輸入;(2)考慮到不同影響因素對票房的影響力不同的現實情況,為了解決以往研究中對影響因素權重平均分配的問題,本文構建了基于加權K-均值和局部BP神經網絡的票房預測模型,以因素影響力為依據對樣本數據進行加權的K-均值聚類,并基于子樣本構建局部BP神經網絡模型進行票房預測.同時通過實際電影數據實驗可以看出,本文構建的基于加權K-均值聚類以及局部BP神經網絡的票房預測模型可以減小票房預測誤差,提高預測的準確度.

本文應用隨機森林進行影響力測算以及采用加權K-均值聚類對數據進行聚類,并采用BP神經網絡模型進行票房預測.在后續的研究中,需要進一步對BP神經網絡模型的構建過程進行優化,并對其中一些參數的選擇以及設置方法進行改進,進一步提高整體票房預測模型的精確度.