聯合CEEMD和改進閾值去噪的初至波識別算法

艾文強,范錦彪,王 燕

(儀器科學與動態測試教育部重點實驗室, 太原 030051)

初至拾取指對傳感器最先接收到的有效波進行拾取。實現高精度定位，在信噪比低的情況下提取可靠的首波到達時間是亟待解決的問題。目前常用的去噪方法是傅里葉變換和小波分析法。采用傅里葉去噪時待分析的信號需要具有一定的線性、周期性或平穩性。對頻率隨時間變化的非平穩信號，傅里葉變換只能給出整體效果，不能完整地掌握某一時刻信號的本質特征，消噪效果不好[1]。采用小波分析算法快速性、時頻性較好，應用廣泛。但同時，小波基函數、分解層數和小波變換的閾值選擇都對去噪效果有影響，選取原則通常取決于經驗，這使得小波變換在分析信號時的自適應性較差。

提出聯合互補集合經驗模態分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)算法[2]和改進閾值去噪的方法。CEEMD是近幾年來發展起來的一種新型自適應信號時頻分析法，根據信號的特點它能自主分解出本征模態函數(Intrinsic Mode Function，IMF)，這是一種適用于分析非線性非平穩信號的方法。常用的閾值去噪方法有硬閾值法、軟閾值法。本文提出了改進的閾值去噪法。新方法克服了硬閾值函數不連續及軟閾值函數中小波系數估計和原系數之間具有固定偏差的缺點。其基本流程為對信號求其包絡，并根據信號的均方差或期望設置合理的包絡值，去噪部分為包絡小于包絡值的部分。對信號進行CEEMD分解后再用新的閾值函數進行改進閾值去噪，既可以保證時頻性又可以很好地解決自適應問題[3]。

初至提取算法，可以分為以下幾類：① 時域分析法，如時窗平均能量法、分形維數法、自回歸模型法、相關法等。時域分析法簡單易行，但對信噪比較低且起跳不明顯的爆炸引起的地震波效果不好。② 時頻分析法，如Fourier、小波變換、S變換，與時域分析法相比，這種方法有很強的的抗噪能力，但受窗長度等參數的影響，一致性不好。③ 綜合分析法，如人工神經網絡法。綜合分析法是目前精度較高、一致性較好的一種方法，但耗時長，實現復雜。④ 本文采用的能量比值算法，這種算法結合初至波識別算法可以快速、準確拾取初至點[4]。

圖1為初至點提取總體流程示意圖。

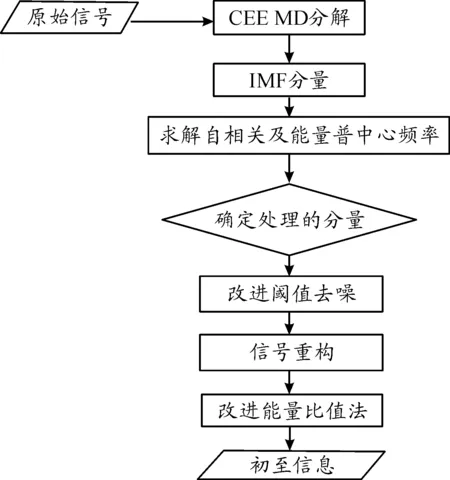
圖1 初至點提取總體流程示意圖

1 EMD算法與CEEMD算法

1.1 EMD算法

經驗模態分解(Empirical Mode Decomposition，EMD)可以被理解為能通過信號極值時間特征量來表示的一種時空濾波算法[5]。經驗模態分解根據信號局部時間特征尺度將信號從小到大分解，并獲得有限個頻率從大到小的IMF。每個IMF必須滿足如下兩個條件：

1) 在整個信號中，極值點的數量和過零點的數量相差不超過1；

2) 在任意時刻，上包絡和下包絡的平均值為0。

通常，實際信號是不符合上述條件的復雜信號。因此，Huang進行了以下假設[2]：任何信號都是由若干本征模態函數組成的；每個本征模態函數可以是線性的，或非線性的，每個IMF的局部零點和極值點數是相同的，并且上包絡線和下包絡線關于時間軸是局部對稱的；任何情況下，信號都可以包含幾個IMF，如果各IMF之間相互混疊，就組成了復合信號。

EMD分解的基本過程為：

1) 找到信號所有的極大值點和極小值點，并通過三次樣條函數擬合信號的最大包絡線e+(t)和最小包絡線e-(t)。上包絡線和下包絡線的平均值被視為原信號的平均包絡，如式(1)所示。

(1)

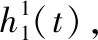
(2)

(3)

一般情況下，上包絡和下包絡的平均值無法為零，所以當符合式(3)時，就判定滿足要求。其中ε為篩分門限，一般取值在0.2到0.3之間。

(4)

3) 用原信號減去c1(t)，得到新信號r1(t)。

r1(t)=x(t)-c1(t)

(5)

對r1(t)重復得到c1(t)的過程，得到第二個IMF分量c2(t),如此反復進行，直到第n階IMF分量cn(t)或余量小于預設值；當剩余量是單調函數或常量時，分解停止[6]。

4) 原信號經分解后得到：

(6)

1.2 CEEMD算法

CEEMD分解基于EMD分解，包括以下步驟：

1) 將n組正負白噪聲加到原始信號，生成的添加噪聲后的信號表示為：

(7)

2) 添加噪聲的信號的EMD分解產生一組本征模態函數分量。

3) CEEMD分解得到的第j個IMF分量表示為：

(8)

與EMD相同，原始信號的噪聲最多的部分位于低階IMF中。該算法需要添加輔助噪聲幅值k和對數N兩個參數，一般當N取100時，k取0.01～0.10。

2 CEEMD分解后的小波閾值去噪及信號重構

在CEEMD將信號分解后，獲得頻率從高到低的有限個本征模態函數，高階IMF對應信號的低頻部分，低階IMF為信號高頻部分。基于CEEMD去噪的主要思想是，對大多數噪聲污染的信號，其主要能量集中在低頻帶，頻帶越高，其包含的能量越少。因此，一定存在某個本征模態函數，使得對于該函數值后的IMFk+1中信號主導，其前k個IMF中噪聲主導，基于CEEMD濾波去噪的主要目的就是尋找到這個IMFk。

自相關是一個信號于其自身在不同時間點的互相關，非正式地來說，它就是兩次觀察之間的相似度對它們之間的時間差的函數。其定義式為[7]：

R(s,t)=E(x(s)*x(t))

(9)

按式(9)分別計算噪聲信號和正弦信號的自相關函數。從圖2、圖3可以看出，噪聲信號的自相關函數在零點處具有自相關函數的最大值，且自相關函數值在其他點處迅速衰減到較小的值；正弦信號，它的最大值也出現在零點處，但由于信號之間的相關性，在其他點處自相關函數值不會快速衰減到很小，而是隨時間差而變化，兩種信號的自相關函數有著明顯的區別。根據該特征，每個IMF自相關處理可以找到噪聲主導和信號主導的分界本征模態函數[8]。

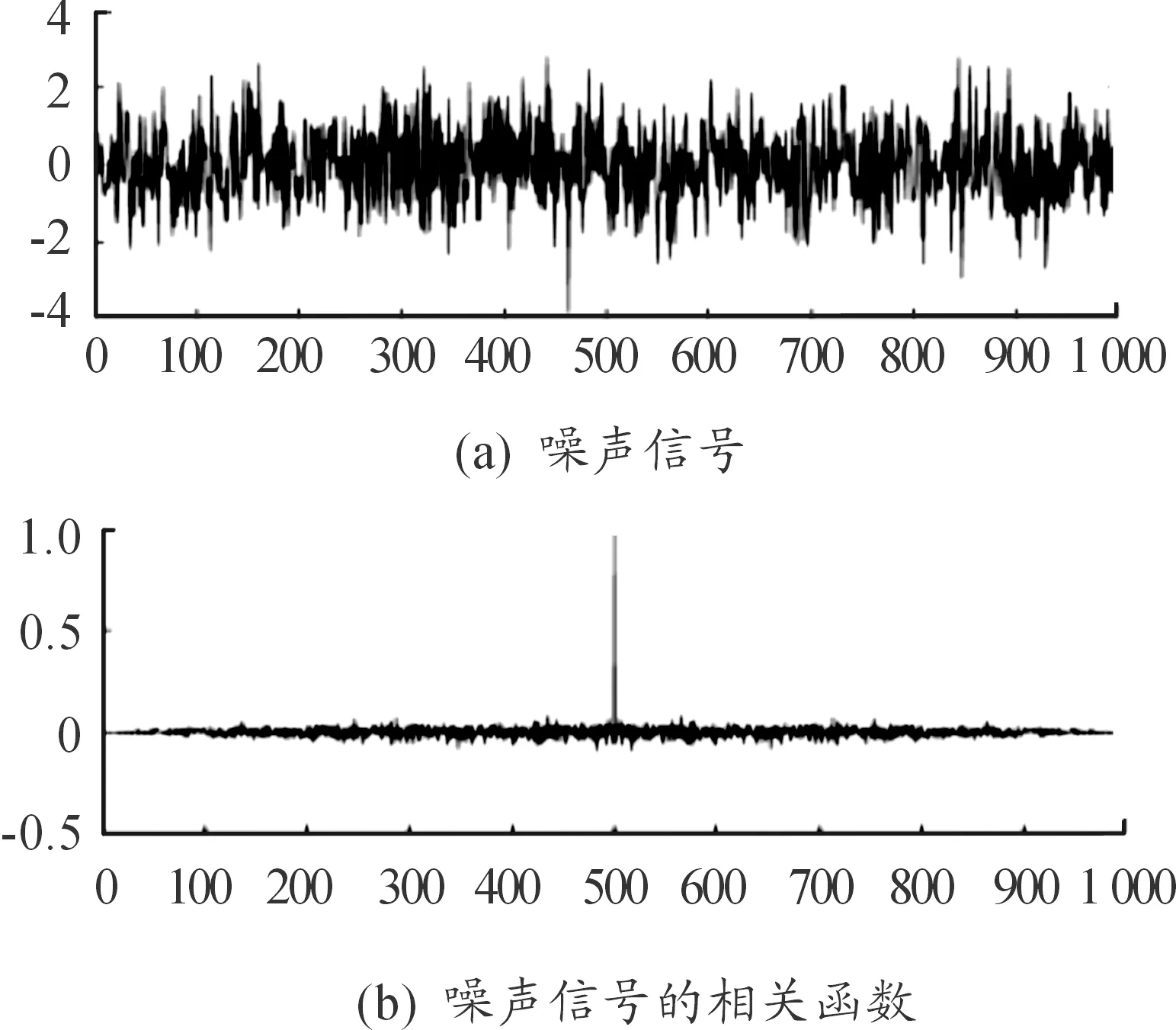
圖2 噪聲信號及其自相關函數

圖3 正弦信號及其自相關函數

軟硬閾值方法雖然得到了廣泛的應用，在一些去噪方法中也取得了較好的效果，但硬閾值函數存在不連續點，容易出現附加振蕩影響結果光滑性；軟閾值使信號連續性很好，比硬閾值函數結果更光滑，但因為與原始信號存在恒定的偏差，嚴重影響重構信號精度。

本文提出了一種新的閾值函數：

(10)

2) |wij|≥λ時，函數是高階可導的，方便進行數學處理。

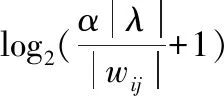
3 能量比值算法原理及實現

能量比方法是基于地震記錄中地震波的瞬時特征拾取初至的。地震信號在到達時間之前和之后有明顯差異，即信號的振幅和能量在到達時間之前保持相對穩定；當地震信號到達時，信號的振幅和能量比到達之前出現了不同水平的突增[9]。對于單一通道信號X(i)，前時窗和后時窗長度為M，總窗長為2M，前時窗和后時窗的能量值分別計算，則后窗能量與前窗能量的比為：

(11)

為了提高結果的穩定和提高可靠性，在式(11)的基礎上增加一個穩定因子S，S的表達式為：

(12)

式中，L為通道信號的長度。則式(11)可改寫為：

(13)

當信號沒有到達時，R(i)的值接近于1；當信號到達時，R(i)的值會突然有很大變化。根據實際情況設定一個閾值P，當R(i)超過這個閾值P時就認為該時窗內是初至波，從而確定初至點。通常還需設定另外一個振幅閾值A，有且僅有R(i)和振幅都超過預設閾值時，才認為識別到初至波。

4 模型建立及測試

1) 模型建立

地震信號在地下傳播時部分鞥量會被吸收，地震信號衰減，本文采用下式合成衰減地震信號。

(14)

其中:S(ω)是的Fourier變換，ω為頻率，k為對應波數，r為傳播距離。

子波選用零相位雷克子波，零相位子波的表達式見式(15)。

w(t)=e-(2πfm/γ)2t2cos2πfmt

(15)

其中:fm代表子波的中心頻率，γ代表子波寬度[10]。

將零相位子波按式(13)可合成一維地震衰減記錄如圖所示。從圖4合成的一維地震記錄觀察，可以發現初至點很明確，但是實際地震記錄往往還有很多噪聲，因此為了更真實的驗證本文方法的有效性，對合成記錄加噪，得到真實地震記錄的模擬記錄，如圖5。

圖4 合成的一維地震記錄

2) CEEMD分解及閾值去噪處理

對圖5的模擬地震記錄進行CEEMD分解，以便后邊進一步處理。其分解圖如圖6所示，共分解為8個IMF分量和一個趨勢。其中階數小的IMF對應于信號的高頻成分，階數大的IMF對應于信號的低頻成分。

圖5 模擬地震記錄

為了找到噪聲起主導作用IMF和信號起主導作用IMF的分界點IMFk，求解出各IMF的自相關函數(如圖7、圖8)。

圖6 模擬地震記錄的CEEMD分解圖

圖7 前4個IMF自相關函數圖

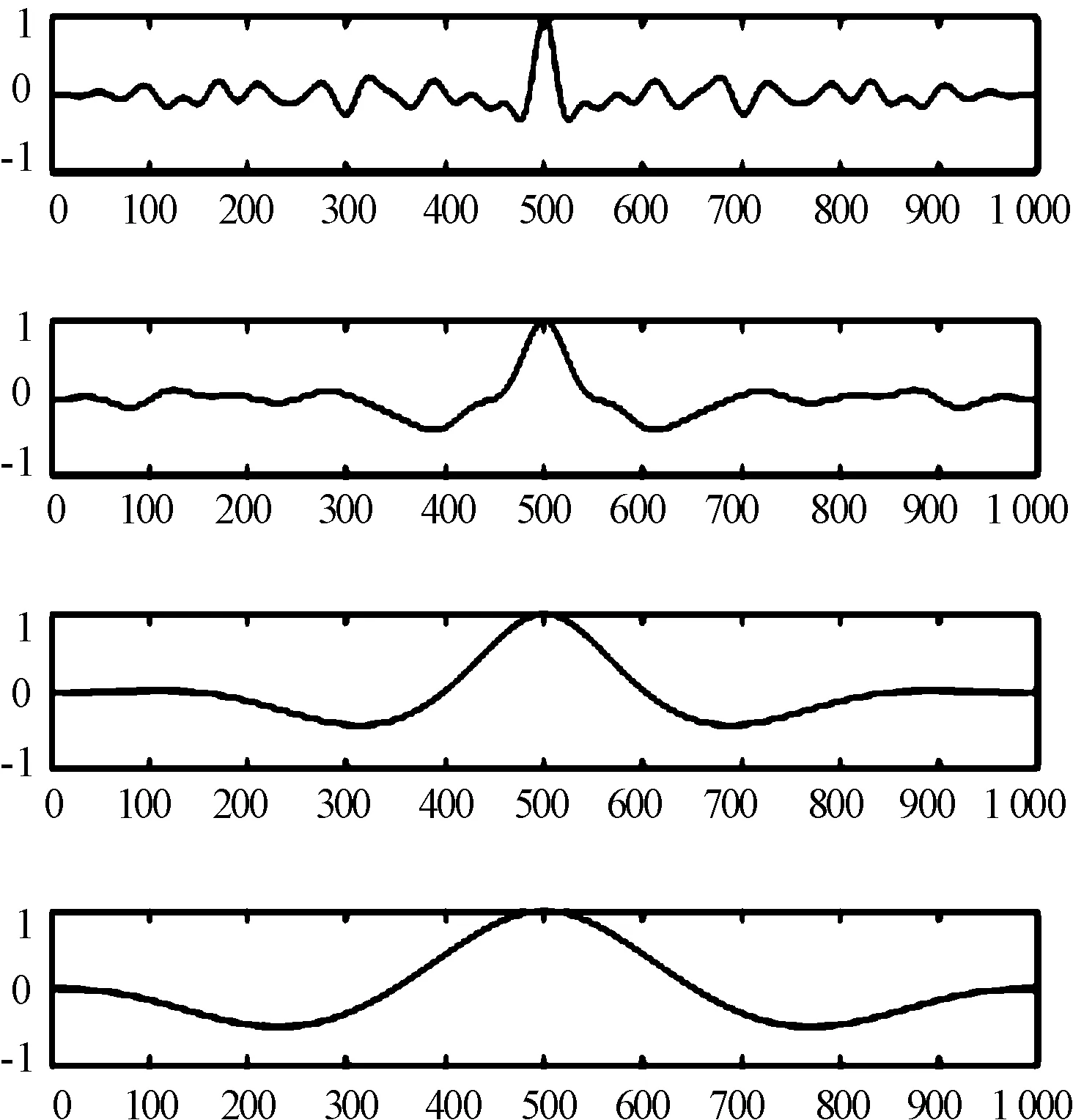
圖8 后4個IMF自相關函數圖

根據信號與噪聲的自相關特點不能直接確定要處理的分量。為了更精確的確定要處理的IMF分量，分別求信號與自相關結果的能量譜 中心頻率，通過對信號的能量譜中心頻率與IMF分量的能量譜中心頻率進行對比，準確得出要確定的IMF分量[11]。

如圖9，可以直觀的判定前3個IMF為噪聲起主導作用，對IMF1～IMF3分量進行改進閾值去噪。圖10為最終去噪后的結果。

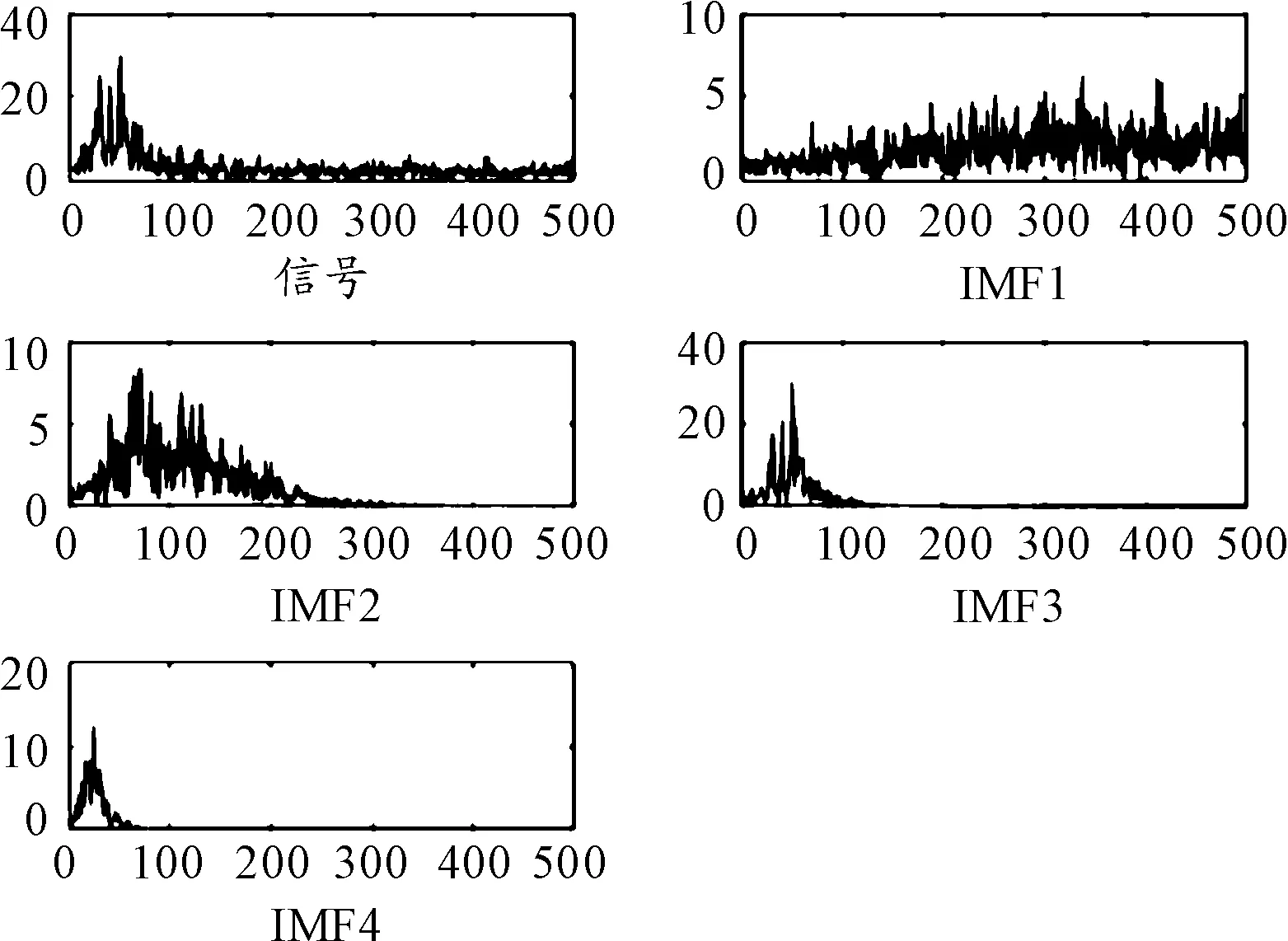
圖9 自相關結果對應頻域圖

圖10 重構信號

3) 初至拾取

對原始信號和經過去噪處理的信號分別求初至，求解結果如表1所示。從表1中可以得出，基于CEEMD和小波閾值去噪的方法對于初至的精確拾取有明顯的改善，該方法能比較精確拾取低信噪比信號的初至。

表1 兩種方法拾取時間

5 實際應用及效果分析

為驗證算法實際情況的可行性，進行了人工地下爆破模擬地震實驗。將3 kg TNT埋設在地下5 m起爆，地震波采集裝置的采樣頻率為20 kHz，采樣總時間為10 s。圖11為地下起爆點起爆后，傳感器獲取的局部震動時域信號圖。

圖11 時域信號圖

為方便計算只對前5 s信號進行CEEMD分解，分解圖如圖12，信號被分解為9個IMF分量及一個趨勢項。

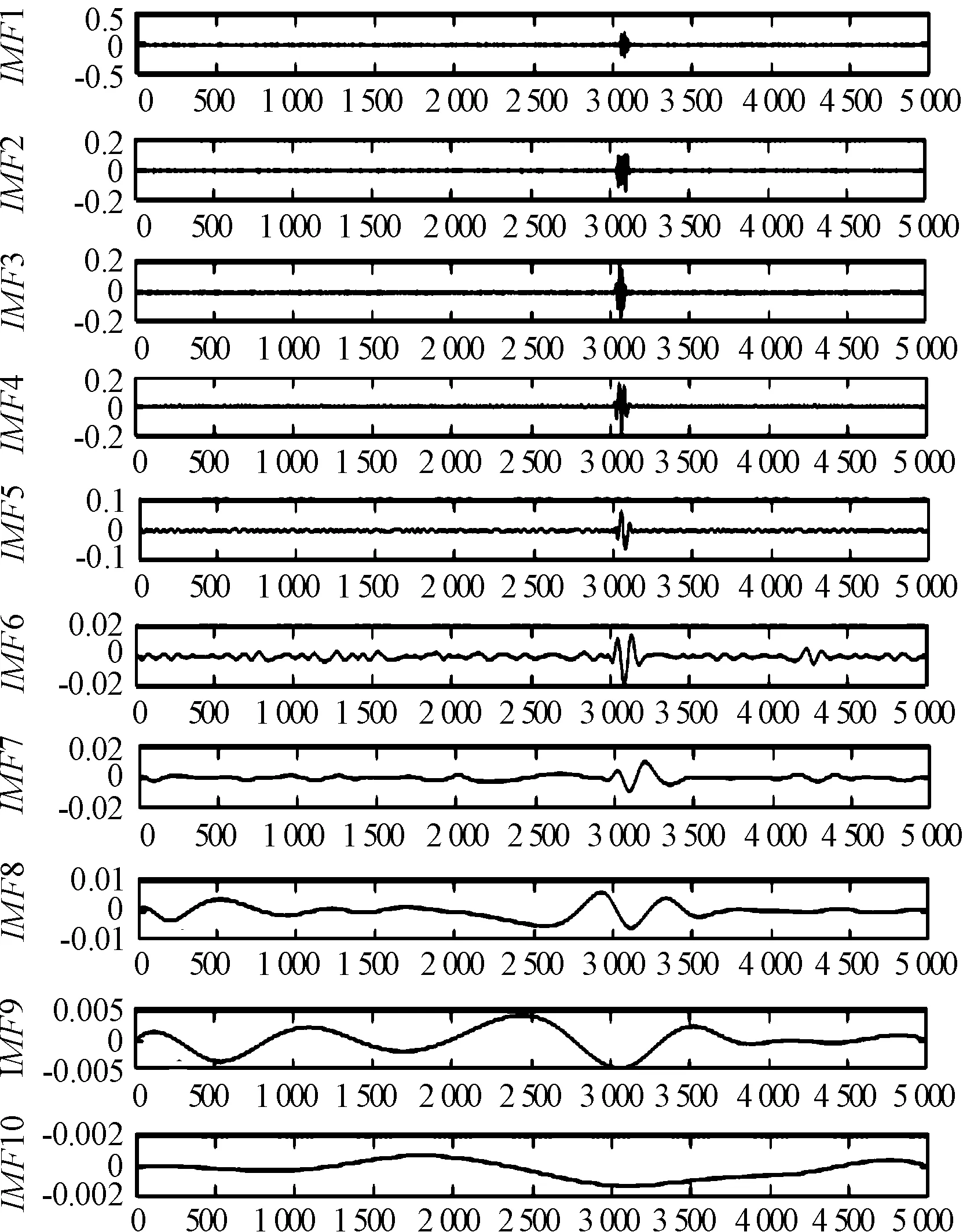
圖12 實測信號CEEMD分解圖

對前四個IMF求解自相關結果如圖13。根據自相關結果，不能很直觀的得出需要對哪幾個分量進行改進閾值去噪。為了更準確的判斷對自相關結果，做傅里葉變換，通過能量譜中心頻率進一步對需要處理的IMF分量進行判斷，如圖14。通過計算主頻的方法可以精確的確定需要對IMF1、IMF2、IMF3進行改進閾值去噪處理。

圖13 前4個IMF分量自相關圖

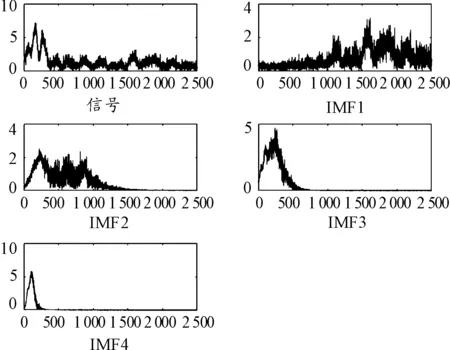
圖14 自相關結果對應頻域圖

去噪后的實測信號重構圖如圖15，表2所列數據為直接通過能量比值法拾取初至時間與去噪后拾取初至時間的結果。

圖15 實測信號重構圖

算法時間/ms直接采用能量比值算法3 059.1本文方法3 047.2

6 結論

1) 聯合CEEMD與改進閾值去噪再利用改進能量比值法可精確提取初至時間。

2) 通過仿真信號和試驗采集實際信號，驗證了算法的穩定性、有效性和高精度性，可以對爆炸產生的地震信號進行初至拾取工作。