基于回歸分析的損傷定位復雜性綜合測度方法選擇

曾 慶，尤志鋒，石 全

(陸軍工程大學石家莊校區 裝備指揮與管理系， 石家莊 050003)

損傷定位是搶修過程執行的第一步，定位的準確性、時效性對整個搶修過程執行的影響很大。損傷定位要求人員對裝備的結構、功能、原理等基礎知識有全面的了解，對裝備的損傷規律、損傷機理等搶修知識亦有較深的掌握，且能夠靈活地運用各種搶修工具，同時具備豐富的損傷定位經驗。損傷部位的多樣性使有些損傷定位較為簡單，利用常識推理即可輕易得出，無須專門訓練，而有些損傷定位則要排除眾多具有迷惑作用的潛在部位，需較多的經驗和技巧，應當經過專門且經常性的訓練。因此，需要對不同損傷事件損傷定位的復雜程度進行區分。文獻[1]引入了損傷定位客觀復雜度，實現了合理區分。文獻[2]利用信息熵法實現了損傷評估復雜性測度，但是沒有細化到損傷定位活動。文獻[3-5]用多因素綜合法對損傷定位復雜性進行了測度，但只是直接給出了從分因素到多因素的綜合方法，沒有給出詳細的論證過程。本文通過對損傷定位復雜性的分析，基于損傷定位流程圖、信息資源圖，利用圖熵模型對損傷定位的難易程度及不確定性進行測度，應用時間數據，通過回歸分析法對復雜性因素綜合方法實施選擇，并對測度結果的有效性做出驗證。

1 損傷定位復雜性因素分析

根據搶修復雜性的概念，損傷定位復雜度是對損傷原因確定過程的難度和不確定性的度量。其與“復雜巨系統”中具有涌現性的“復雜性”不同[4]，損傷定位復雜性是在“損傷定位難度”概念上的進一步拓展。

損傷定位的復雜性主要是由“損傷本身的隨機性、多樣性，裝備功能結構的層次性、關聯性”而引起的損傷定位所需信息的不全面、不準確所造成的。損傷模式不像平時的故障模式那樣有較強的規律可循[5]。一個損傷現象可能有多個不同的損傷原因。裝備的任何部件都有可能發生多種損傷模式。新條件下，武器裝備的功能越來越多、集成化越來越高、結構越來越復雜，這些都將導致本來就具有隨機性的損傷定位過程又具有不確定性，損傷定位變得更復雜。因此，損傷定位復雜性主要表現為損傷層次結構的復雜性和損傷信息轉化的復雜性。

1) 損傷層次結構的復雜性。裝備損傷具有層次性。低層次的損傷發生是高層次的損傷發生的充分不必要條件。由低層次到高層次逐漸發展的這種關系，就是損傷層次的“縱向性”。當裝備功能結構某一層次的某個部件發生損傷后，由于裝備各個構件之間的相互聯系以及損傷的傳播關系，將引起與損傷部件相關的其他部件損傷發生。這樣可能導致同一層次多個損傷的發生。這就是損傷層次的“橫向性”。

顯然，裝備的結構越復雜，層次越多，損傷層次的縱向性就可能越明顯。縱向層次性越多，損傷的根本原因就越可能處于裝備功能結構的低層，損傷現象就屬于間接損傷，要找到損傷根本原因的難度與不確定性就越大。橫向層次越多，由上一級損傷定位到下一級損傷的難度就越大、不確定性就越高。因此損傷層次結構的復雜性是損傷定位復雜性的根本原因。

2) 損傷信息獲取的不確定性。損傷信息是能判斷出損傷根本原因的所有信息，包括損傷現象、損傷證據、損傷模式及損傷影響等。這些信息有些是顯性的，即通過肉眼或簡單的操作即可以得到。而有些是隱性的，需要借助于功能檢測、使用檢查等操作才能獲取。獲取信息所需的操作越多，其不確定性就越大。

綜上，損傷定位復雜性可分為損傷縱向層次復雜性、損傷橫向層次復雜性、損傷信息獲取數量復雜性及信息獲取質量的復雜性四個維度。經過分析這四個因素可以用損傷定位流程圖與資源信息圖，通過圖熵法對四個指標進行賦值。

2 復雜性因素賦值

損傷定位流程是輔助損傷樹進行深入分析的重要工具。資源信息圖是對損傷定位所需的工具、人員、信息等資源的一種表達。兩者都能夠用圖的形式進行描述，且都可以體現出損傷定位的復雜性，因此可以利用圖熵法對其賦值[4]。

2.1 圖熵法

圖熵即圖形的熵。其可以用Shannon公式計算：

(1)

式(1)中：Ai為圖中定義的類；n為類的數量；P(Ai)為類A的發生概率，其計算公式如下：

利用上述公式，根據不同的節點分類規則，就可以實現圖形的一階熵和二階熵的求取。

一階熵，根據圖中節點的輸入輸出程度對節點進行類別劃分。當兩個節點的輸入和輸出相同時，則將兩個節點歸為同一類別，以此類推。則一階熵的計算方法為：

(2)

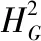
(3)

2.2 損傷定位資源信息圖

資源信息圖是進行損傷定位所需的資源的組織與表達，包括人力資源、物質資源及各種信息資源。它既要能反映信息的數量又要可以反映信息獲取的質量。其詳細的組成及生成方法如下。

資源信息圖的元素主要是邊和點。“點”主要是代表資源及信息，“邊”代表它們之間的關系。考慮到定位過程中可能需要協同操作，這里將“協同”作為一種“虛擬資源”加入資源信息圖，其為數組型的，數組當中存儲參與協同的所有人員。

將資源都可以看作變量，資源的屬性作為變量值。資源的屬性如表1所示。

表1 資源屬性

明確了變量類型及取值以后，就可以明確資源信息圖的生成方法如下：

將當前的步驟作為根節點。

第一層節點：根據變量種類，在將所需人員、工具、資料的名稱以及協同四個節點中選擇需要的作為第一層節點；如工具需要電壓表、扳手則在第二層相應加入這兩個節點。

末層節點：人員變量的根節點是修理工D3；工具變量的根節點是維修通用工具W；資料變量的根節點是現場X。

中間節點：工具節點、人員、資料。縱向：根據第一層節點級別，從相應的級別開始，逐層加入下一級別節點，直到根節點為止；協同節點，將協同節點看做一個“根節點”在其下一層加入參與協同的所有人員，并按照上述原則逐漸加入中間節點，直到末層節點為止。

若某種類型的資源所需數量大于1個，則這個變量就先連接一個變量池(表明所需的數量)然后變量池下面再連接變量的值，具體過程可參考文獻[6]。

四類變量并不是所有的損傷定位過程都有。損傷定位過程從以上4種變量中選擇所需變量,沒有用到的變量，在控制圖中無需體現。

圖熵分為一階熵(又叫彩色信息內容)和二階熵(或稱結構信息內容)。從物理意義上講，一階熵代表圖形的規模(如節點數量)，二階熵表示圖形規則(如對稱性)[7]。

損傷定位流程圖及資源信息圖縱向層次性反映的是圖形的規模與數量，與一階熵對應，橫向層次性反映的是圖形的規則與質量，與二階熵對應。因此基于損傷定位流程圖與資源信息圖可以實現對損傷定位復雜性四個影響因素的賦值。

3 因素綜合方法選擇

從某裝備維修數據庫中找出14個損傷事件(如圖1所示)的損傷定位時間數據，結合2.3給出的復雜性量化方法，對每個損傷事件的4個指標進行求取，得到如表2所示的數據[1]。

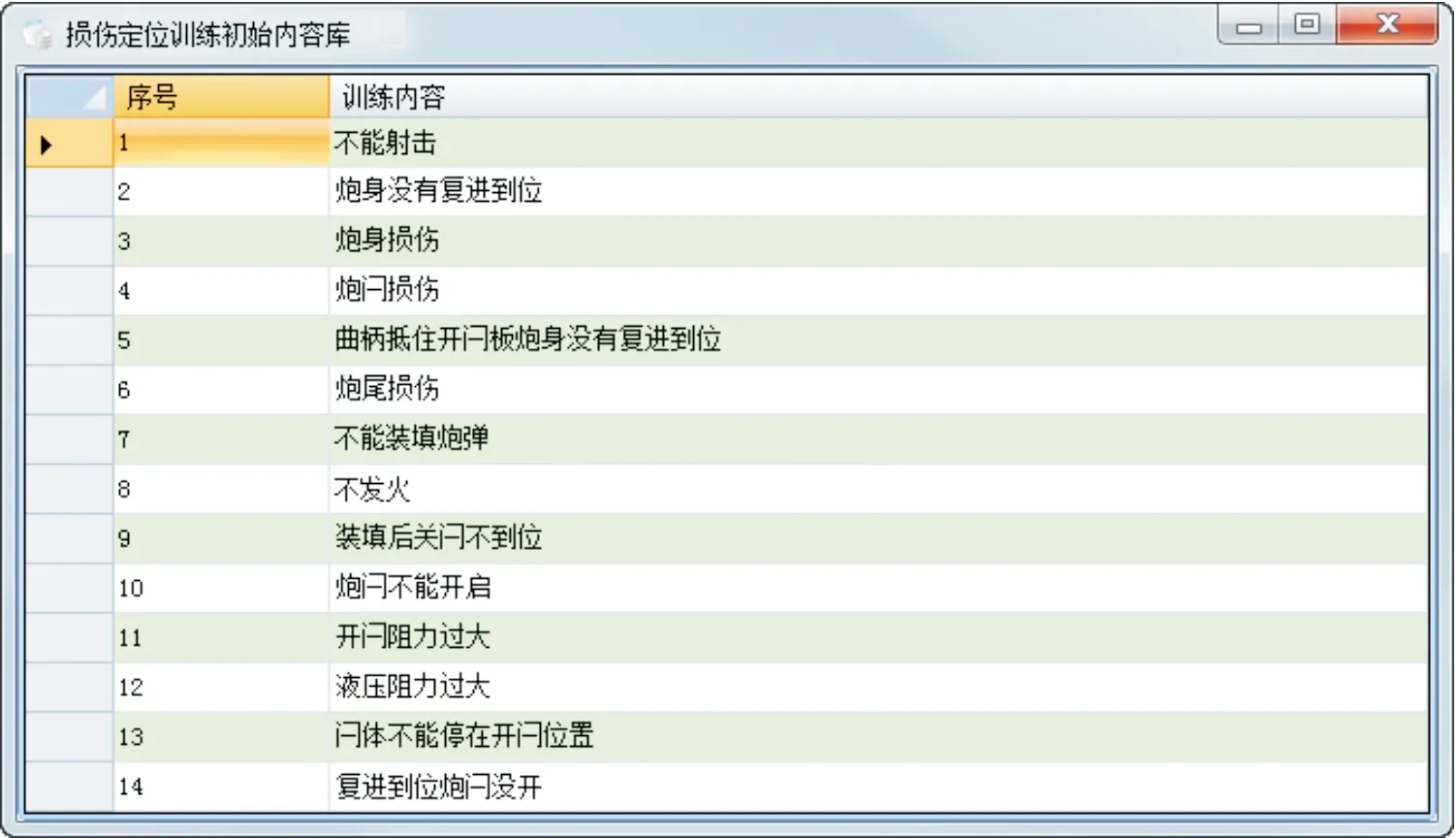
圖1 損傷事件

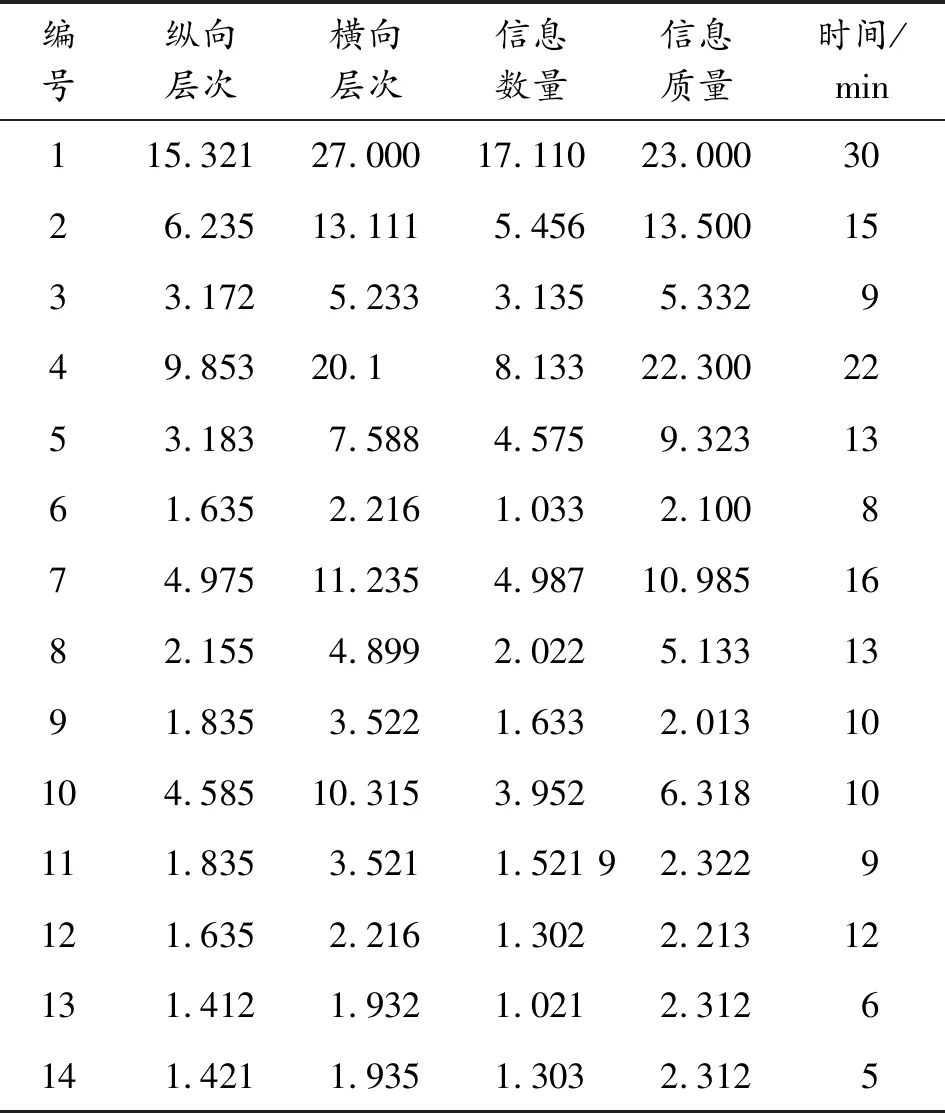
編號縱向層次橫向層次信息數量信息質量時間/min115.32127.00017.11023.0003026.23513.1115.45613.5001533.1725.2333.1355.332949.85320.18.13322.3002253.1837.5884.5759.3231361.6352.2161.0332.100874.97511.2354.98710.9851682.1554.8992.0225.1331391.8353.5221.6332.01310104.58510.3153.9526.31810111.8353.5211.521 92.3229121.6352.2161.3022.21312131.4121.9321.0212.3126141.4211.9351.3032.3125

復雜性綜合屬于多因素綜合的范疇。目前多因素綜合的方法主要有線性加權法和非線性加權法。由于復雜性的非線性，一般不采用線性加權。歐幾里得范式、信息熵、聯合指數、幾何平均等方法都是典型的多因素綜合的非線性加權法。根據文獻[9]的思路，利用不同方法得到的復雜性綜合結果與損傷定位時間進行方差分析與回歸分析，將效果最好的方法作為綜合的方式。

歐幾里德范式：

(4)

式(4)中，α,β,γ,δ分別為損傷定位流程4個復雜性影響因素的權重，由專家通過層次分析法或根據已有數據通過擬合法得到。

幾何平均：

(5)

聯合指數：

(6)

信息熵法：

令∑=αHIG+βHAG+γHWG+δHDG，則：

(7)

利用表2所示的數據，根據上述公式可以得到表3所示的復雜性綜合結果。

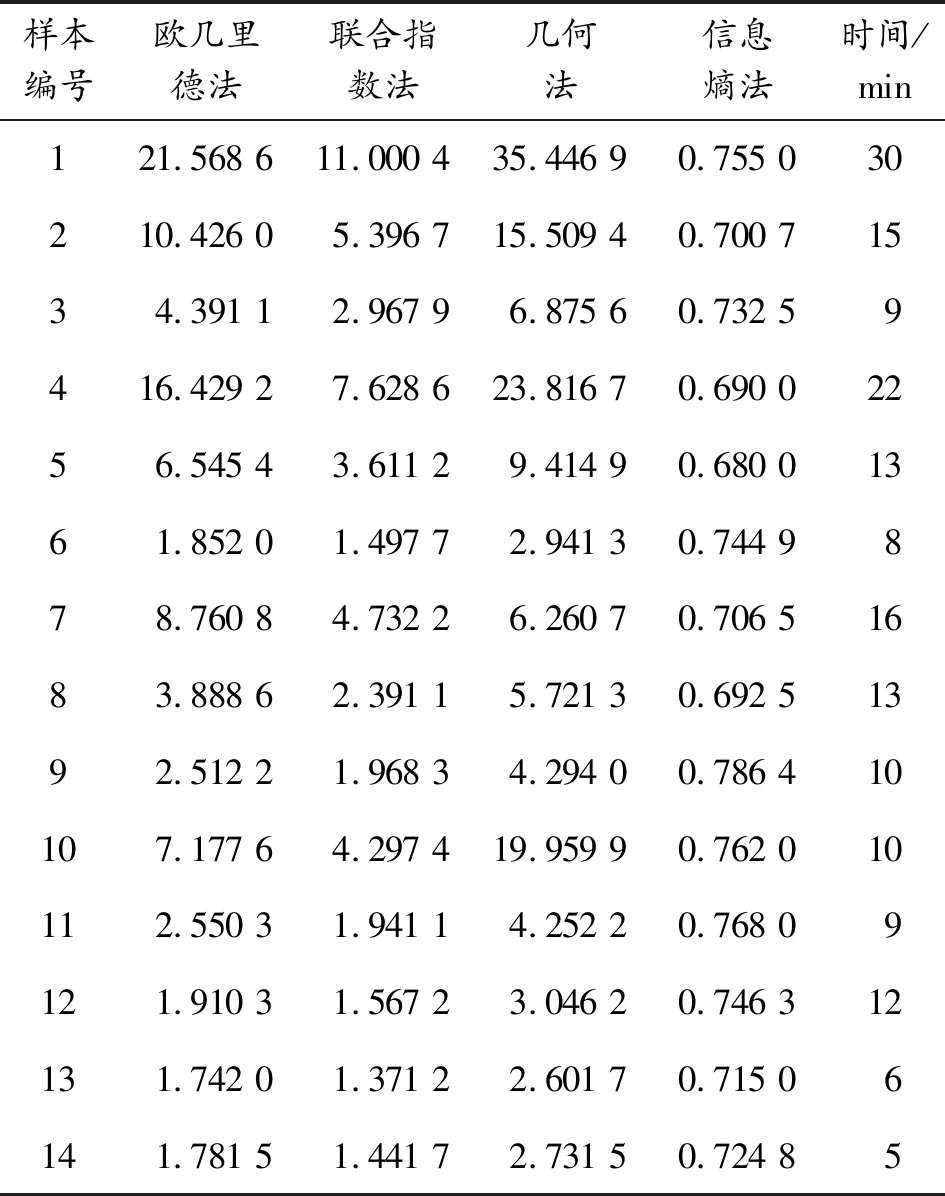
表3 四種綜合方法求得的客觀復雜度結果

利用表3所示的數據進行回歸分析可得如圖2、圖3、圖4、圖5及表4所示的結果。由于這里采用的是曲線回歸，因此使用代表曲線回歸關系的復確定系數R2及F統計值來判斷回歸效果的優劣，而不用相關系數來判斷。

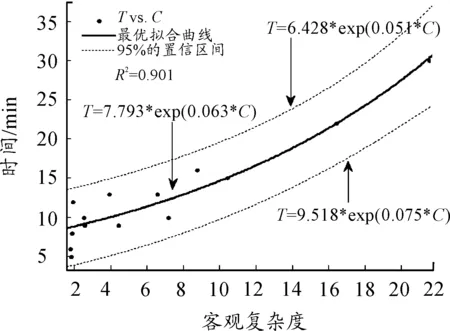
圖2 歐幾里得范式綜合法回歸結果

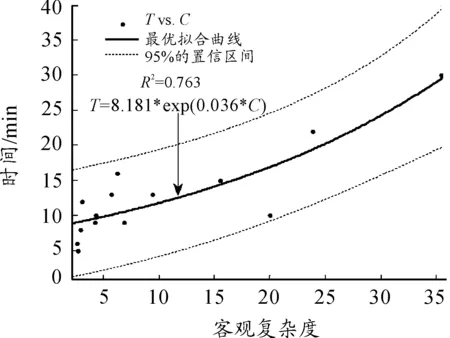
圖3 幾何平均綜合法回歸結果

圖4 聯合指數綜合法回歸結果

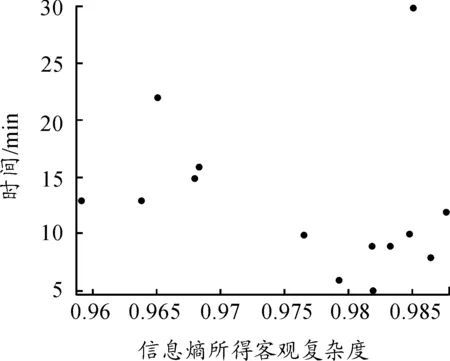
圖5 信息熵綜合法散點圖

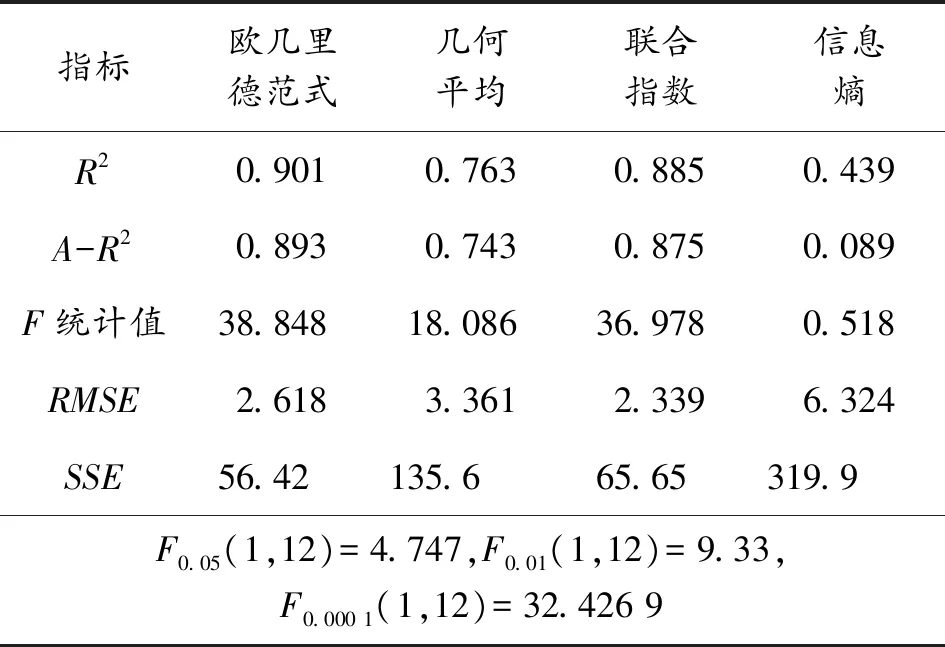
指標歐幾里德范式幾何平均聯合指數信息熵R20.9010.7630.8850.439A-R20.8930.7430.8750.089F統計值38.84818.08636.9780.518RMSE2.6183.3612.3396.324SSE56.42135.665.65319.9F0.05(1,12)=4.747,F0.01(1,12)=9.33,F0.000 1(1,12)=32.426 9

由上面的結果可以看出信息熵綜合結果的效果最差，其點分布較散亂，沒有一定的規律(如圖5所示)。歐幾里德范式綜合法效果最好，但是聯合指數法的效果僅次于歐幾里德范式法。歐幾里得范式需要知道各個影響因素的權重，而聯合指數法則不需要。因此當各個因素的權重較易獲得，且精確度較高時利用歐幾里得范式綜合法進行綜合；而當權重獲取較困難，或精度不高時利用聯合指數法進行綜合。

4 結論

歐幾里德范式綜合法對復雜性影響因素進行綜合的效果說明利用損傷定位流程圖與資源信息圖，基于圖熵法對復雜性影響因素進行量化是合理的，能夠很好的映損傷定位過程的客觀復雜性。