基于凸包的最小體積有向包圍盒生成算法

胡志剛 秦啟飛

摘 ???要：針對復雜物體三維點集的建模問題，提出一種基于凸包的最小體積的封閉有向包圍盒生成算法.對凸包和其最小體積有向包圍盒的關系進行分析，總結了其4種邊面接觸類型.通過枚舉凸包中邊的所有可能的組合，唯一確定包圍盒的最優方向.實驗證明，該算法可以快速生成符合模型體積特征的最小有向包圍盒，且擬合效果良好.

關鍵詞：有向包圍盒;幾何計算;凸包;三維點集;圖搜索

中圖分類號：TP30 ?????????????????????????????文獻標志碼：A

Algorithm for Finding Minimum Volume Oriented

Bounding Boxes Based on Convex Hull

HU Zhigang，QIN Qifei

（School of Software，Central South University，Changsha 410083，China）

Abstract： A new method was presented for computing the tight-fitting enclosing minimum volume oriented bounding boxes for constructing the model of complex object point sets in three dimensions. The relationship between the convex hull and its minimum volume oriented bounding box with the smallest volume was analyzed，and four kinds of edge contact types were summarized. The optimal box orientations are uniquely determined by combinations of edges in the convex hull of the input point set. Empirical evidence shows that this process always yields the globally minimum bounding box by volume feature， which concludes that this method provides a good simulation.

Key words： oriented bounding box;computational geometry;convex hull;three-dimensional point set;graph search

物體的包圍盒廣泛應用于圖像處理、模式識別、碰撞檢測、模具分型設計和機械控制等領域[1-2].目前應用最廣泛的OBB（Oriented Bounding Box，有向包圍盒）根據物體本身的幾何形狀來決定包圍盒的大小和方向，可以對原模型進行緊湊的擬合[3].對于給定的三維點集，怎樣高效而準確地得到其最小有向包圍盒一直是國內外學者關注的問題[4].

一般考慮物體的所有頂點在空間的分布，通過不同的算法找到最佳方向，以確定OBB包圍盒的幾個軸.主要使用數值和統計優化方法來找到非最優、但在實際使用中足夠好的近似值.目前的主流方法是使用主成分分析（PCA）[5]，根據物體表面的頂點，計算特征向量來估計點集中最大擴展的方向，并作為OBB的主軸.這個過程必須使用凸包上的連續集合表示來完成，否則近似值可能是無界差的[5].為了獲得接近最優的結果，Barequet 和HarPeled提出一個（1+α）逼近方案[6]，而另一方面，Larsson和 K？覿llberg則提出可以采用預定義的啟發式方法來獲得更好的計算速度[7].國內的陳柏松等[4]提出了基于非線性主成分分析的最小包圍盒計算方法，在計算時間和運行結果上都取得了不錯的效果，但是該方法利用了頂點之間的連接信息，無法處理無連接關系的點集數據.

還有學者提出使用粒子群優化[8]和遺傳算法[9]來計算最佳結果，取得了不錯的效果.但這些算法中包含隨機因子，不能保證在所有情況下都找到最佳包圍盒.

法國的Chang等提出混合包圍盒旋轉識別算法HYBBRID，采用遺傳搜索方法對SO（3，R）的所有方向進行暴力搜索[10].對于給定OBB的候選方向，將模型重復地投影到與當前候選OBB的主軸相對應的平面上，將其轉化為2D問題，使用Toussaint的旋轉卡尺方法[11]在線性時間內進行求解.這減少了暴力搜索的難度，將問題轉化為在單位半球中搜索較優的起始方向向量.通過不斷重復計算得到最佳OBB的取向.然而，在該方法中搜索是在連續的空間上進行的，不能通過對一組離散的取向進行采樣.

綜合上述分析，已知的使用近似值，數值計算或啟發式方法的算法，效果都不夠出色.

本文提出一種快速準確的幾何算法來解決該問題.首先對三維點集的凸包進行分析，總結了凸包和其最小體積有向包圍盒的4種邊面接觸類型.通過枚舉凸包所有邊可能的組合，選取包圍盒的最優方向.實驗證明，該算法可以快速生成符合模型體積特征的最小有向包圍盒，且擬合效果良好.

1 ??系統模型及問題描述

1.1 ??問題描述

由于模型內部的點對問題的解決沒有任何幫助，所以本研究基于凸包的邊上進行操作.可以使用Quick Hull算法[12]或其改進方法[13-14]在O（n log n）時間復雜度內計算點集的凸包.

最小有向包圍盒生成問題定義如下.

輸入：三維點集構成的凸包頂點集V，邊集E，表面集F;

輸出：最小有向包圍盒O.

1.2 ??相關符號與概念

為了更好地進行后續討論，首先對相關符號和概念進行介紹.

定義1 ??支持頂點 （Supporting Vertices）. 在凸包中，方向向量n的方向上的一個或多個最高頂點，成為支持頂點，表示為Supp（n）.

定義2 ??對向 （Antipodal）. 對于兩個頂點v1和v2，如果存在一個方向向量n，使得v1 ∈Supp（n）和v2 ∈Supp（-n），則稱v1和v2的位置關系為對向.其幾何描述為：如果可以找到封閉OBB的某個方向，使得凸包上的兩個頂點位于OBB的相對面上，則該兩個頂點是對向的.

定義3 ??側向 （Sidepodal）. 對于兩個頂點v1和v2，如果存在兩個方向向量n1和n2，使得 v1∈Supp（n1），v2 ∈Supp（n2），并且n1·n2，則稱v1和v2互為側向.其幾何含義是，對于一個閉合的OBB，如果可以找到一個方向使得頂點v1和v2位于該OBB相鄰的兩個相鄰面上，則稱v1和v2互為側向.

支持、對向和側向的概念同樣可以用來表示凸包的邊和面的關系.如果一條邊e和頂點v分別位于該OBB的兩個相鄰面，那么也稱邊e和頂點v相互側向.

如果x是凸包的頂點或邊，則凸包中x的所有對向頂點的集合將表示為AntiV（x），凸包中x的所有對向邊的集合表示為AntiE（x）.同樣，SideV（x）和SideE（x）表示x所有側向的頂點和邊的集合.此外，對于上述的側向集合，SideV（e1，e2）表示集合的交集SideV（e1）∩ SideV（e2）的簡寫.顯然，如果一條邊e：v1→v2，是特征x的對向邊或側向邊，那么邊e上的頂點v1和v2也具有相同的性質.即：

若e∈AntiE（x），那么：{v0，v1}∈AntiV（x），

若e∈SideE（x），那么：{v0，v1}∈SideV（x），

若e∈SideE（x1，x2），那么： {v0，v1}∈SideV（x1，x1）.

因此，遍歷對向邊集或側向邊集，等效為遍歷其頂點的集合.值得注意的是，對于側向關系，反過來則不成立.即使兩個相鄰的頂點對于特征x是側向的，連接它們的邊卻不一定也與x側向.

符號N（v）表示頂點v的鄰居頂點集合.從凸包內部測量的連接邊e的兩個相鄰面之間的角度通常稱為邊e的二面角（Dihedral Angle）.因為凸包是凸形，所以所有的二面角的范圍都在（0，180）內.最后，在邊e兩側指向凸包外側的兩個相鄰面的法線表示為f <（e）和f ?>（e）.這些法向量具有以下屬性：

引理1 ??如果OBB的面與凸包的邊e齊平，那么OBB的該面的（非歸一化的）法向量n為：

n = f <（e） + （f ?>（e） - f ?<（e））*t，t[0，1]

證 ??該公式直接來自線性插值.t = 0的值對應于OBB與法向量f <（e）的面齊平的情況，t = 1的值對應于與法向量f ?>（e）的面齊平的OBB.由于邊的二面角從不為0，所以線性內插值不會產生簡并零向量.

證畢.

實際上，我們可以使用幾何的方法將凸包的頂點和邊與支持函數相關聯.

引理2 ??給定凸包的一個頂點v和一條邊e，當且僅當存在一個方向向量n使得v∈Supp（n）且（n·

f <（e））（n·f ?>（e））≤0時，頂點v∈SideV（e）.

證 ??根據引理2，與邊e齊平的OBB的面的法向量n2具有性質：n = f <（e） + （f ?>（e） - ?f <（e））*t.當且僅當存在向量n使得v∈Supp（n）和n·n2 = 0時，頂點v與邊e側向.將法向量進行替換，給出下列公式：

n·（f <（e） + （f ?>（e） - ?f <（e））*t） = 0，t[0，1] ???（1）

公式左側是關于t的線性表達式，所以當t取0和1時，表達式取得極限值，分別為：n·f <（e）和n·

f >（e）.因此，當且僅當n·f <（e）和n·f >（e）中一個為正數，一個為負數時，該方程有解.即：

n·f <（e） ≤ 0，且n·f >（e） ≥ 0，或者

n·f <（e） ≥ 0，且n·f >（e） ≤ 0.

將兩個表達式相乘就可以得到引理2.

證畢

對于凸包的頂點和邊，不論是對向還是側向，都是非傳遞的關系.本文將通過對凸包的頂點圖進行計算來得到相關關系，具體的實現算法在1.3節給出.

1.3 對向和側向關系判斷算法

基于1.2的論述，給出以下判斷頂點與邊和兩條邊是否為對向關系的算法.

圖1中算法輸入為：頂點v，邊e;輸出為：頂點和邊是否是對向關系.圖2中算法輸入為：凸包的兩條邊e1，e2，輸出為：使得兩條滿足對向關系的單位向量.同樣，可以使用圖3中算法來判斷兩條邊是否為側向關系.圖3中算法輸入為：凸包的邊e1，e2;輸出為：兩條邊是否是側向關系.

2 ??最小體積有向包圍盒生成算法

2.1 ??凸包與其OBB的4種接觸類別

該算法總體策略是：通過計算通過凸包邊的組合唯一確定OBB方向，而不是對球體中的所有可能定向方向進行暴力搜索.

Freeman和Shapira[11]提出并證明了，在二維情況下，凸包的最小面積的包圍矩形的一條邊必定與凸包的一條邊共線，因而考慮凸包的每條邊，以此作為凸包的包圍矩形的一條邊.在三維情況下，通過對大量實例的分析，提出以下假設：

假設1 ??凸包至少有三條不同的邊，與其最小體積OBB包圍盒的表面共面，其中至少兩條邊位于OBB的相鄰面上.

該假設意味著凸包的特定邊e位于OBB的特定表面f上.基于上述假設，根據凸包及其封閉OBB的邊緣接觸不同情況，分為以下4個類別，與OBB接觸的邊以粗線條突出顯示：

1）類別A：凸包三條邊位于OBB的三個相互相鄰的面.

該類別的實例如圖4-A所示，其中頂點坐標為：

0： （1，0，2）; 1： （1，4，3）; 2： （4，0，4）; 3： （4，2，1）; 4： （3，2，0）.

凸包的邊1→2，1→4和2→3位于OBB的三個相互相鄰的面，頂點0位于與邊1→2所在平面相對的面上.

2）類別B：凸包三條邊位于OBB的三個面，其中兩個是對面.

該類別的實例如圖4-B所示，其中頂點坐標為：

凸包的邊0→1，0→3和2→3位于OBB的三個面.其中，邊0→1和2→3位于兩個相對面.

3）類別C：凸包三條邊位于OBB兩個相鄰的面.

凸包的三條邊位于OBB的兩個相鄰面，即凸包的一個面和一條邊與OBB重合.該類別的實例如圖4-C所示，其中頂點坐標為：0：（0，0，0）;1：（5，2，2）;2：（5，5，0）;3：（10，0，0）.

凸包的三條邊位于頂點0→2→3形成的平面，頂點1位于該面的對面.需要注意的是，在上述示例中，相鄰面的交邊0→3，剛好位于凸包與OBB重合面，但這種情況不總是發生.

4）類別D：凸包兩條邊位于OBB三個面，其中兩個是對面.

OBB的三個不同面上僅與凸包的兩條邊齊平.這是一種特殊情況，其中凸包的邊與OBB的邊重合.此時，OBB上必須存在兩個包含凸包邊的對向面，否則將包圍盒和凸包沿公共共享邊投影到2D平面（將共享邊縮減至一點）時，所得2D矩形沒有與所得2D多邊形的任何邊重合，因此不是最優解.該類別的實例如圖4-D所示，其中頂點坐標為：0：（0，4，2）;1：（0，4，4）;2：（2，4，2）;3：（3，0，1）;4： （1，4，0）.

在該示例中，最小體積OBB僅與凸包的兩條邊齊平，但是這些邊位于OBB的三個不同的面.頂點0是不與OBB接觸的內部頂點.

2.2 ??搜索最小體積封閉OBB包圍盒

通過搜索測試圖2所示的每種類別情況.

1）對于類別A 和類別 B

對凸包中每條邊e1∈E進行遍歷，尋找可能位于OBB的相鄰側面上的所有邊 . 然后，針對類別A，搜索OBB中與先前兩個面相互相鄰的第三個面上的所有邊 .對于類別B，搜索OBB中與邊e1接觸的面相對的第三面上的所有邊 .

2）對于類別C

對凸包中面f∈F進行遍歷.確定OBB的一個面法線n1. 對邊集F中任意一邊e1，遍歷e3∈SideE（e1）.

3）類別D

類別D可以看作類別B中e1 = e2時的特殊情況，因此在搜索類別B時隱式處理此類別，因此不需要單獨進行測試.其幾何含義時，邊可能和自身是側向的.

執行上述迭代的過程如圖5所示.算法偽碼包含幾個中間過程函數.函數ComputeBasis（e1，e2，e3） 和函數CompleteBasis（n1，e）是兩個空間幾何計算函數，作用是通過三條邊或者一條邊和一個向量建立包圍盒的基底.函數ComputeOBB計算凸包的六個極端頂點，分別對應OBB的每個面，為計算OBB的方向提供基礎. 使用Dobkin-Kirkpatrick層次數據結構，最多需要O（log n）時間.函數RecordOBB是常數時間的計算，它計算新創建OBB的體積，與之前記錄的OBB進行比較，并存儲兩者中較小的一個.

算法中輸入為：凸包頂點集V，表面集F，邊集E;輸出為：最小包圍盒OBB.算法包含兩個單獨的頂級循環.第一個用（行1-行13）來處理類別A，B和D，第二個循環（行14-行21）處理類別C.在第一個循環結構中，外層循環（行1-行13）確定凸包的一條邊，這是一個O（n）的操作.第二層循環（行2-行13）遍歷第一條邊的所有側向邊.時間復雜度為

O（log n + SideE（e1））.

第一個最內圈循環（3行-7行）針對類別A的情況進行處理，時間復雜度為O（log n + SideE（e1，e2））.首先建立OBB的方向，對于給定的三條邊，調用函數ComputeBasis計算基底（n1，n2，n3）. 然后，調用函數ComputeOBB和RecordOBB處理該基底.

第二個最內圈循環（行8-行13）針對分類B的情況進行處理，時間復雜度為：O（log n + AntiE（e1））.對滿足條件的邊進行迭代，首先使用算法2計算OBB一個面的法向量，通過函數ComputeBasis計算基底，然后調用函數ComputeOBB和RecordOBB完成計算.

最后，第二個頂級循環體（行14-行21）針對類別C進行遍歷.凸包中每個面都可以直接確定一個法向量.內圈循環（行17-行21）時間復雜度為：

O（log n + SideE（e1）），對邊e1的對向邊集進行遍歷，為OBB的第二個軸確定一個候選方向，以完成后續計算.

第一循環結構中的步驟總數為：E（log n + SideE（e*））（log n+SideE（e*，e*）+AntiE（e*））log n，

第二個循環為F（log n + SideE（e*））log n. 在

標準球型Sphere（n）數據集上，算法運行時間是

O（n3/2（log n）2）. 在最壞的情況下，如在圓柱型Cylinder（n）數據集的情況下，算法運行在O（n3 log n）時間.

3 ??最小體積有向包圍盒生成算法

3.1 ??實驗數據

本文進行了大量的實驗來測試算法的擬合效果和執行效率.實驗使用C++編程語言和開源軟件包MathGeoLib[15]實現，所有實驗均運行于Dell T700 型號PC機器，處理器為Intel Core i7 3.6 GHz，內存為16 GB，操作系統為Windows 10專業版.測試程序使用Microsoft Visual Studio 2017編譯器構建，采用64位編譯，所有基準測試中均為單線程執行.

實驗選用兩個不同的數據集進行驗證，分別為： 1）標準球體數據Sphere（n），n表示凸包中頂點數量，模型通過程序自動生成.2） GAMMA Group 3D網格研究數據庫[16]，包含5個不同類別的數據集，共計2 088種不同的3D模型.

1）55個模型來自數據集2001;

2）381個模型來自數據集ANIMALS;

3）530個模型來自數據集ARCHITEC;

4）437個模型來自數據集GEOMETRY;

5）685個模型來自數據集MECHANICAL.

3.2 ??實驗結果分析

對于標準球型數據集Sphere（n），首先采用Quick Hull算法計算凸包頂點，然后使用本文所述算法搜索其最小體積OBB包圍盒，以下所有指標均不包括運行Quick Hull算法所需的時間.如圖6所示，對于相同半徑的球體，當凸包頂點數達到500時，已經可以較好地還原物體形狀.而本文所述算法搜索到的最小體積封閉OBB包圍盒，可以對所有的凸包進行緊密的包圍，取得了良好的效果.

算法運行時性能如圖7所示，其中X軸表示數據凸包中頂點的數量，Y軸表示計算OBB所對應的時間，實際數據以細線繪制.結果表明，當凸包頂點數在10 000以下時，算法表現與預期的O（n3/2（log n）2）性能回歸曲線有較好的匹配.

由于包圍盒僅取決于模型的凸包，因此先將GAMMA Group真實模型數據集中的模型進行預處理.

算法的擬合效果如圖8所示，可以看出對復雜物體模型，算法所計算出的包圍盒也可以進行非常緊密的包圍.圖9中散點圖顯示了算法的性能情況，X軸為該對象的凸包上的點數，Y軸表示計算OBB所需的時間（s）.這個基準測試的結果表明，大多數現實世界模型對象的計算性能與Sphere（n）的情況非常相似.如圖9所示在參與測試的2 088個模型中，大部分模型表現接近最佳預期.

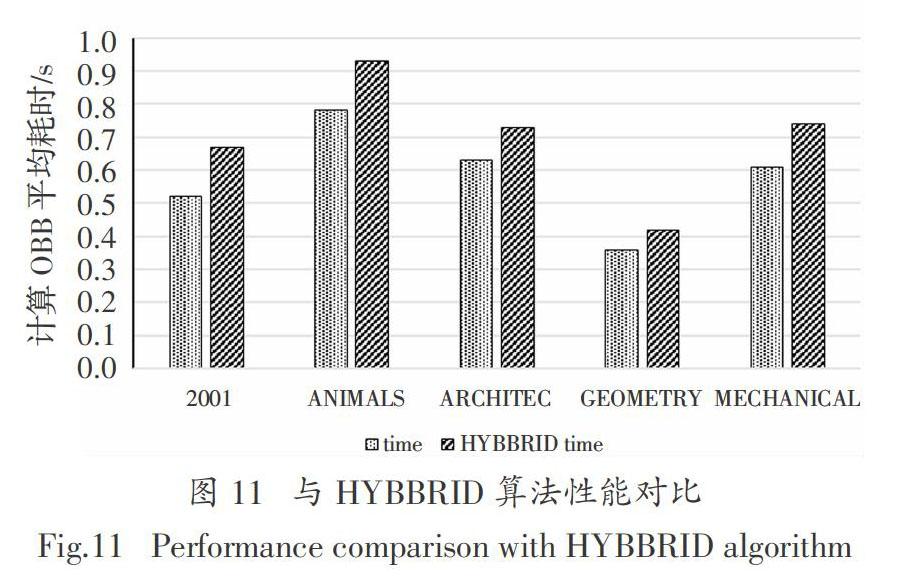
在GAMMA Group數據庫的5個不同數據集中，分別對本文所提算法和文獻[10]中的HYBBRID算法進行對比試驗，包圍效果如圖10所示.因為模型個體形狀差異較大，所以選取算法在不同數據集中最優情況，中位數情況和最差表現比較所得OBB包圍盒與原模型的體積之比，比值越小表示可以更緊密的包圍.其中Optimal、Median、Max為本文所提算法數據，與之對比的是HYBBRID Optimal、HYBBRID Median、HYBBRID Max 三個指標.從圖中可以看出，本算法在最優情況下，包圍效果與HYBBRID

算法相同或者略優;在中位數情況下明顯優于HYBBRID算法;在最壞情況下，表現比HYBBRID算法略差.而從圖11可以看出，在5個不同的數據集上，本算法的平均耗時均低于HYBBRID算法，具有更好的計算性能.

4 ??總結與展望

本文首先對三維點集凸包中點線面關系進行分析，總結了凸包與其最小OBB包圍盒的4種邊面接觸類型.并提出了一種計算三維點數據的最小定向包圍盒的新算法，該方法首先針對輸入點集構造凸包，通過快速迭代凸包邊的組合，唯一確定OBB的最優方向.最后通過實驗證明，該算法能夠精確地找到所有模型的最小OBB包圍盒，且具有更好的性能表現.

該算法是一個離散的過程，不使用連續統計的數值優化或迭代.因此，該方法是穩定和可預測的.同時，與以前公開的結果不同，該方法相對容易實現，并且可以以不同的方法對其進行編程，以平衡實現復雜度與運行時復雜度.

此外，因為算法在凸包的邊集合上只讀順序遍歷，它可以很容易被改寫為并行算法，因此也適用于處理大數據集.

針對模型極端復雜的場景，該算法的包圍效果還存在進一步優化空間.且該算法只適用于計算最小體積OBB包圍盒，暫未考慮對于追求最小表面積的OBB包圍盒場景.因此，后續研究可以就復雜模型的包圍優化，以及針對最小表面積情況進行進一步探索.

參考文獻

[1] ???史旭升，喬立紅，朱作為. 基于改進OBB包圍盒的碰撞檢測算法[J]. 湖南大學學報（自然科學版），2014，41（5）：26—31.

SHI X S，QIAO L H，ZHU Z W. Algorithm of collision detection based on improved oriented bounding box [J]. Journal of Hunan University（Natural Sciences），2014，41（5）：26—31.（In Chinese）

[2] ???陳華. 確定任意形狀物體最小包圍盒的一種方法[J]. 工程圖學學報，2010，31（2）：49—53.

CHEN H. A method to generate the minimum bounding boxes for shape-arbitrary objects [J]. Journal of Engineering Graphics，2010，31（2）：49—53. （In Chinese）

[3] ???O′ROUKRE J. Finding minimal enclosing boxes[J]. International Journal of Computer & Information Sciences，1985，14（3）：183—199.

[4] ???陳柏松，葉雪梅，安利. 基于非線性主成分分析的最小包圍盒計算方法[J]. 計算機集成制造系統，2010，16（11）：2375—2378.

CHEN B S，YE X M，AN L. Minimum bounding box calculation based on nonlinear principle component analysis [J]. Computer Integrated Manufacturing Systems，2010，16（11）：2375—2378. （In Chinese）

[5] ??DIMITROV D，KNAUER C，KRIEGEL K，et al. Bounds on the quality of the PCA bounding boxes[J]. Computational Geometry Theory & Applications，2009，42（8）：772—789.

[6] ???BAREQUET G，HAR-PELED S. Efficiently approximating the minimum[J]. Journal of Algorithms，2001，38（1）：91—109.

[7] ???LARSSON T，KLLBERG L. Fast computation of tight fitting oriented bounding boxes[J]. Game Engine Gems，2011，2： 3—19.

[8] ???BORCKMANS P B，ABSIL P A. Oriented bounding box computation using particle swarm optimization[C]//European Symposium on Artificial Neural Networks. Bruges，Belgium，2010.

[9] ???孫殿柱，史陽，劉華東，等. 基于遺傳算法的散亂點云最小包圍盒求解[J]. 北京航空航天大學學報，2013，39（8）：995—998.

SUN D Z，SHI Y，LIU H D，et al. Solution of minimum bounding box of scattered points based on genetic algorithm [J]. Journal of Beijing University of Aeronautics and Astronautics，2013，39（8）：995—998. （In Chinese）

[10] ?CHANG C T，GORISSEN B，MELCHIOR S. Fast oriented bounding box optimization on the rotation group SO（3，R）[J]. ACM Transactions on Graphics，2011，30（5）：1—16.

[11] ?FREEMAN H， SHAPIRA R. Determining the minimum-area encasing rectangle for an arbitrary closed curve[J]. Communications of the ACM， 1975， 18（7）：409—413.

[12] ?BARBER C B，DOBKIN D P，HUHDANPAA H. The quickhull algorithm for convex hulls[J]. ACM Transactions on Mathematical Software，1996，22（4）：469—483.

[13] ?IMAI H，IRI M. Polygonal approximations of a curve[J]. Computational Morphology，2014，6（1）： 71—86.

[14] ?李仁忠，楊曼，劉陽陽，等. 一種散亂點云的均勻精簡算法[J]. 光學學報，2017，37（7）：89—97.

LI R Z，YANG M，LIU Y ?Y，et al. An uniform simplification algorithm for scattered point cloud[J]. Acta Optica Sinica，2017，37（7）：89—97. （In Chinese）

[15] ?A C++ library for linear algebra and geometry manipulation for computer graphics[EB/OL]. https：//github.com/juj/MathGeoLib. 2017 March.

[16] ?GAMMA GROUP，2008. 3D meshes research database. [EB/OL]. https：//www-roc.inria.fr/gamma/gamma/download/ download.php.