端盤截齒切削海底塊狀硫化物載荷特性

李艷，陸鵬，李鈺晴

(1.中南大學機電工程學院，湖南長沙，410083；2.深海礦產資源開發利用技術國家重點實驗室，湖南長沙，410012)

與陸地礦相比，深海礦產資源具有極高的金屬品位。目前，越來越多的國家進入工業化發展階段，對金屬的需求不斷加大，開發深海礦產資源是大勢所趨。海底塊狀硫化物(seafloor massive sulfide，SMS)由于其具有賦存水深較淺、距離陸地較近、經濟價值較高等優點被國內外學者認為是最有可能成為深海采礦的首選對象[1?4]。海底塊狀硫化物礦床多位于1 000～3 000 m 海平面以下，承受10～30 MPa的海水圍壓作用。海底塊狀硫化物在開采過程中，由于深海環境復雜并且存在海水圍壓作用，其剝離破碎技術是開采過程中一大難點。目前，國內外學者認為類似于陸地采煤機螺旋滾筒的截齒切削是一種最佳的塊狀硫化物切削方法[5?6]，其中，端盤位于深海采礦車滾筒的端部，端盤截齒數超過滾筒截齒總數的1/2，工作環境極其惡劣，截齒負荷高，消耗的功率占工作機構總消耗的1/3 左右[7]。為了改善滾筒截割過程中的受力條件，增強采礦車工作穩定性和使端盤參數與工作過程自適應，必須掌握高海水圍壓條件下端盤截齒切削塊狀硫化物礦體過程的載荷特性。PARASIE等[8]通過離散單元法建立了高靜水圍壓下硬巖切削過程的模型，該模型揭示了在圍壓作用下，巖石裂紋擴展能力變弱，切削阻力大大增加；HELMONS 等[9]使用離散單元法研究了圍壓和孔隙壓力對于飽和巖切削進程的影響，發現圍壓越大，Peclet 數對切削力的影響越大，而圍壓和Peclet 數的增加均會使得切削力增大。VERCRUIJSSE 等[10]通過離散單元法研究海底鈷結殼的破碎機理，發現在海水圍壓的作用下海底巖石的塑性增強，切削時裂紋的產生和擴展變得更加困難；LI等[11]基于離散單元法研究圍壓對于巖石破碎進程的影響，發現隨著圍壓和巖石強度增加，裂紋沿法向的傳播受到抑制，切削力增加，截割比能耗增加；李艷等[12?13]采用有限單元法研究了不同圍壓對塊狀硫化物破巖機理的影響，發現隨著圍壓增加，截齒受到的截割阻力和進給阻力都會顯著增大；HUANG等[14]使用有限單元法研究了側壓對截齒破巖破碎力的影響，發現當側壓小于臨界側壓時，平均峰值切削力隨側壓增加而增加，而當側壓大于臨界側壓時，平均峰值切削力隨側壓增加而減小。宋揚等[15]通過有限單元法研究了端盤截齒旋轉截割煤巖的動態過程，發現端盤截齒更容易出現疲勞斷裂，安裝參數存在最優單側截割工況；PARK等[16]采用線性切割機試驗與有限元分析相結合的方法，從破碎效率、結構穩定性和耐用性研究截齒的最優截割工況，發現正傾斜角對提高切削效率和結構穩定性有利；郝志勇等[17]采用有限單元法建立了采煤機端盤截齒斜切截割模型，發現隨著切向安裝角的增大將會極大地影響滾筒截割力矩。由于離散單元法的二維模型無法考慮圍壓下端盤截齒破巖過程的側向力，而其三維模型的計算量巨大，因此，使用較多的仿真方法是三維有限元方法[18]。影響三維有限元方法計算端盤截齒切削SMS 礦體精度的關鍵因素是巖石本構模型，目前采用較多的巖石本構模型是Mohr-Coulomb(M-C)模型、Drucker-Prager(D-P)模型和Holmquist-Johnson-Cook模型(HJC 模型)。M-C 模型在區分巖石拉壓強度的同時，能夠考慮靜水壓力的影響，但由于其在主應力空間中的屈服面是六棱錐形狀，具有奇異點，會導致計算結果不收斂；D-P模型雖然考慮了中間主應力的作用，但不能反映π 平面上的拉伸子午線和壓縮子午線的不同。通過比較，HJC 模型能較好地反映SMS 礦體高孔隙率性質特點和圍壓對材料的影響[12?13,19]。本文作者基于ABAQUS 平臺，借助VUMAT 接口編制多金屬硫化物HJC本構模型代碼。自定義的HJC本構模型可以充分考慮實驗數據所描述的礦體力學特性。在原始HJC 模型的基礎上，考慮切削過程中巖石的損傷和強化；損傷法則定義為以等效塑性應變和塑性體積應變為變量的損傷累積，強化法則定義為各項同性強化；流動特性定義為關聯塑性流動。通過對比SMS 樣品的三軸壓縮實驗結果與實驗模型結果一致的三軸壓縮仿真模型，驗證自定義本構模型的有效性。然后，建立三維截齒旋轉切削模型，并使用經過驗證的自定義本構模型作為SMS 材料本構模型，研究圍壓、圓周切向安裝角、軸向傾斜角和二次旋轉角對破巖載荷和載荷波動系數的影響規律。

1 礦體本構模型

1.1 本構模型定義

圖1所示為巖石的應力?應變曲線的3個階段：彈性階段、塑性階段和斷裂損傷階段，其中，D為損傷因子。本構模型的定義便是要針對這3個階段進行定義。圖2所示為截齒切削塊狀硫化物時計算每一個礦體網格單元應力－應變狀態的積分推導過程。選用強健的徑向返回算法，算法基于彈性預估，然后通過塑性校正對比試算應力和屈服應力，通過更新應力等張量完成積分推導。在推導過程中，所有參與推導的變量均假定為時間增量步末尾t+?t時對應的變量，即時間增量步末尾的應力表示為σt+Δt，而增量步起始的應力表示為σt，因此，SMS 礦體HJC 本構模型從以下3個方面描述：應力更新算法、損傷和單元失效刪除。

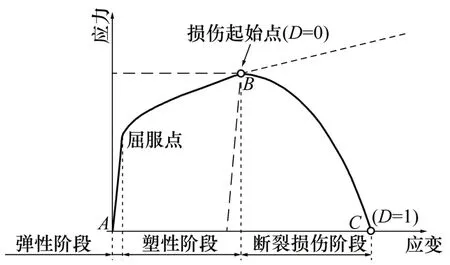
圖1 礦體應力?應變曲線Fig.1 Stress?strain curve of orebody

1.1.1 應力更新算法

在材料試算過程中，應變ε分為彈性應變εe和塑性應變εp，即

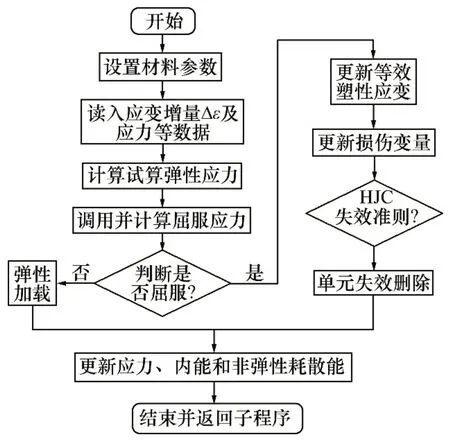
圖2 VUMAT積分推導流程Fig.2 Integral derivation flow of VUMAT

在彈性階段，試探應力張量由彈性應變增量引起，由廣義Hook定律得出：

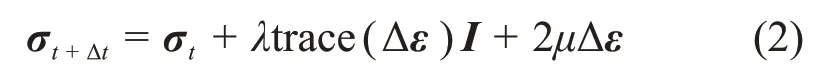
其中：λ為lame常數，；E為彈性模量；μ為泊松比；trace為張量矩陣求跡函數；I為轉動慣量；Δε為應變增量。而試探應力的Mises等效應力計算式為

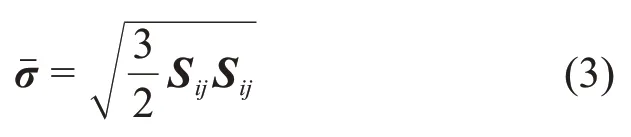
其中：Sij=σij-δijσkk/3，為試探應力的偏應力張量；系數為增量步t時試探應力的主應力。當各應力應變張量之間滿足屈服條件時，材料進入塑性階段，屈服面函數σy可以表示為

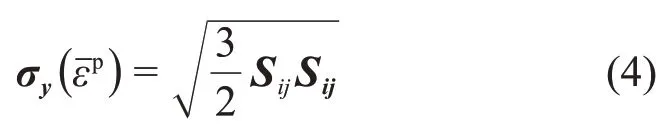
此時，材料已發生屈服，繼續增大載荷，根據關聯塑性流動法則可以得到應力變化引起的屈服面的法線方向與塑性增量的關系。圖3所示為塑性流動法向法則示意圖，其中，dεp為塑性應變增量。

塑性應變增量dεp和等效塑性應變張量dεˉp的計算表達式如下：

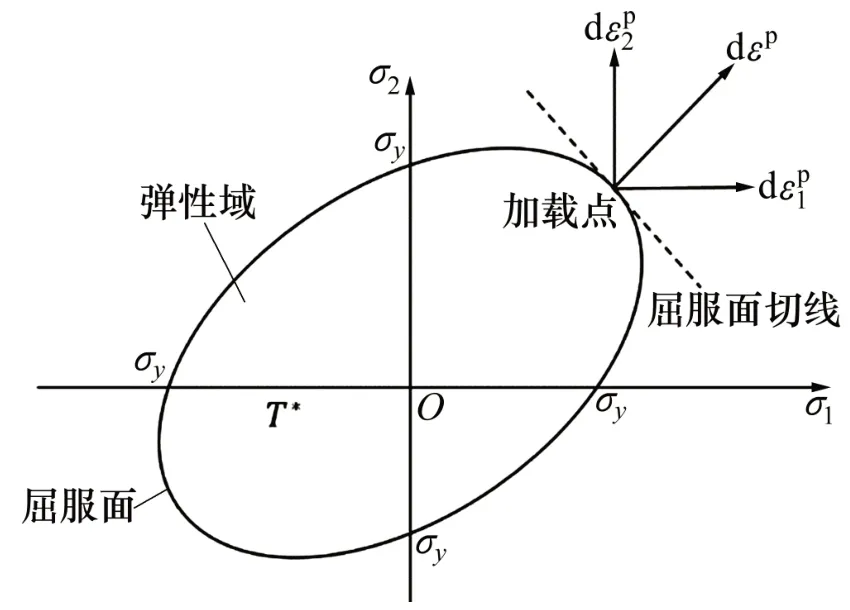
圖3 塑性流動法向法則示意圖Fig.3 Schematic diagram of plastic flow rule

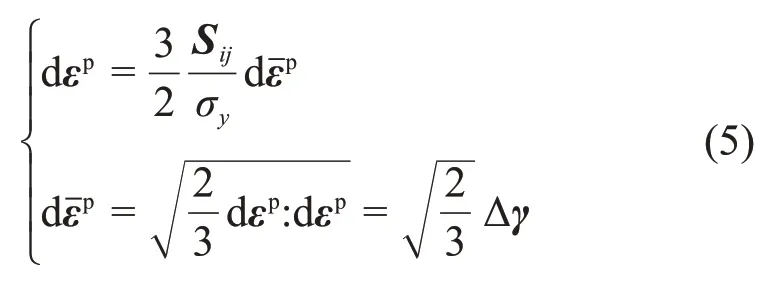
進而得到塑性應變非負標量的計算式：

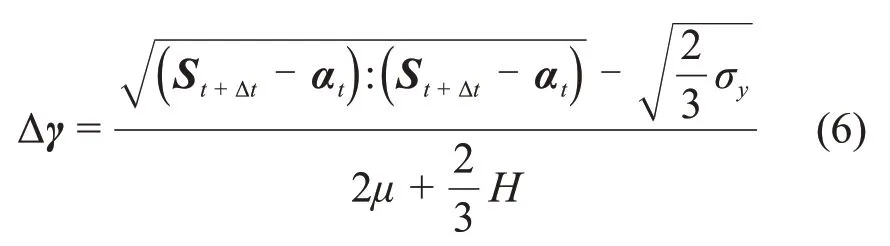
其中：αt為背應力張量；H為塑性模量“:”為2個張量的雙點積運算符。

結合應力補償更新算法，得到應力張量、背應力張量和等效塑性應變的更新表達式：

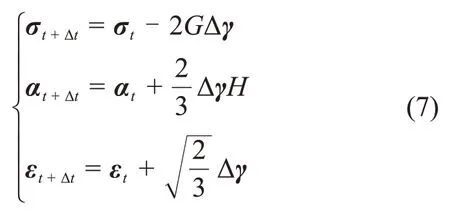
其中：G為剪切模量；G=E/[2(1+μ)]。

1.1.2 損傷和失效刪除

塊狀硫化物礦體的破碎過程由塑性體積應變和等效塑性應變引起的損傷累積控制：

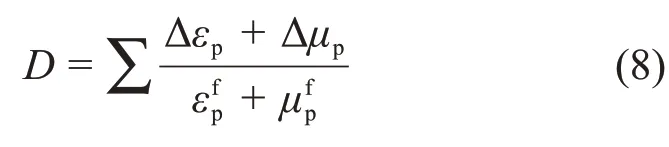
其中：D為損傷因子；Δεp和Δμp分別為1次計算中等效塑性應變增量和塑性體積應變增量；為常壓下破碎的塑性應變，；D1和D2為損傷常數；P?=p/fc為標準化靜水壓力，p為實際靜水壓力；fc為巖體礦石材料的準靜態單軸抗壓強度；T*=T/fc，為標準化峰值抗拉應力，T為材料可以承受的最大拉伸強度。當損傷因子累積超過材料所能承受的最大損傷因子D時，此時，礦體材料積分點傳遞的質量、剛度、應力和應變增量變為0，這樣，其在整體結構計算中就不再發揮作用而退出工作機制。本構模型的推導過程采用Fortran 語言編制成代碼，每次迭代計算時，ABAQUS通過VUMAT接口調用這段代碼。

1.2 VUMAT單元驗證

為驗證VUMAT的合理性，采用單個單元立方體模型進行三軸壓縮測試。數值模型的邊界條件如圖4(a)所示。載荷加載方式為軸向位移加載，等效應變速率為1.0 m/s。在ABAQUS/Explicit中實施計算，結合通用動力非線性有限元軟件ANSYS/LS-DYNA 計算結果和塊狀硫化物樣品三軸壓縮實驗結果[20?21]，分別提取計算得到的不同圍壓下單元的抗壓峰值強度，計算結果如表1所示。

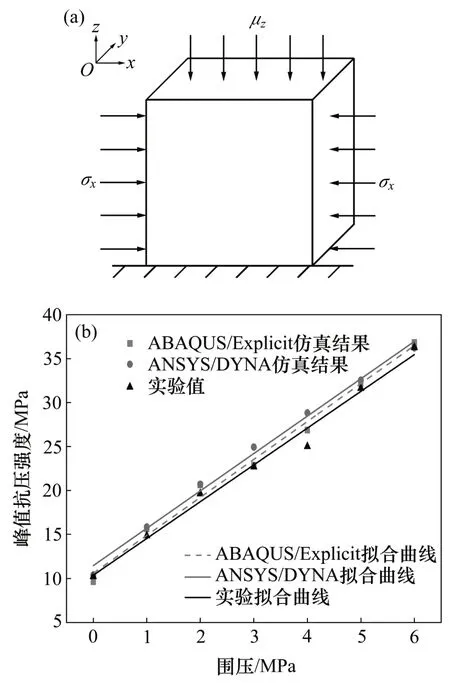
圖4 三軸測試仿真模型和仿真結果Fig.4 Triaxial test numerical model and results

表1 抗壓峰值強度仿真值與實驗值Table 1 Simulation and experimental values of peak compressive strength MPa

抗壓強度?圍壓曲線對比如圖4(b)所示。從圖4(b)可看出：在HJC 模型參數一致的條件下，ABAQUS/Explicit和ANSYS/LS-DYNA仿真擬合曲線均與實驗擬合曲線較吻合，可認為自定義HJC材料子程序能更好地模擬塊狀硫化物在壓縮損傷時的力學特性。

2 仿真模型的建立

2.1 端盤截齒安裝參數

端盤截齒安裝角度如圖5所示。端盤截齒安裝參數主要包括圓周切向安裝角β0、軸向傾斜角β1(一次旋轉角)和二次旋轉角β2。圓周切向安裝角β0為齒身軸線與截齒齒尖切線正交線間的夾角，其值會影響截齒和齒尖與礦體接觸形式、截齒受力。軸向傾斜角β1為齒尖截面(通過滾筒軸線并且貫穿截齒齒尖)上齒身軸線與螺旋滾筒徑向線之間的夾角，若其取值合適，則可以使齒座與礦體互不干涉，避免齒座磨損。二次旋轉角β2為齒尖截面正交面上齒身軸線與滾筒徑向線之間的夾角，合理的二次旋轉角可以減少齒座磨損。為了分析各安裝參數對端盤截齒破巖破碎性能指標的影響，采用單因素變化法，每個因素按照工程施工經驗取值，其中，切向安裝角取3個不同值，軸向傾斜角取4個不同值，二次旋轉角取2個不同值。數值模擬時，安裝參數默認值為表2中括號中的數值。

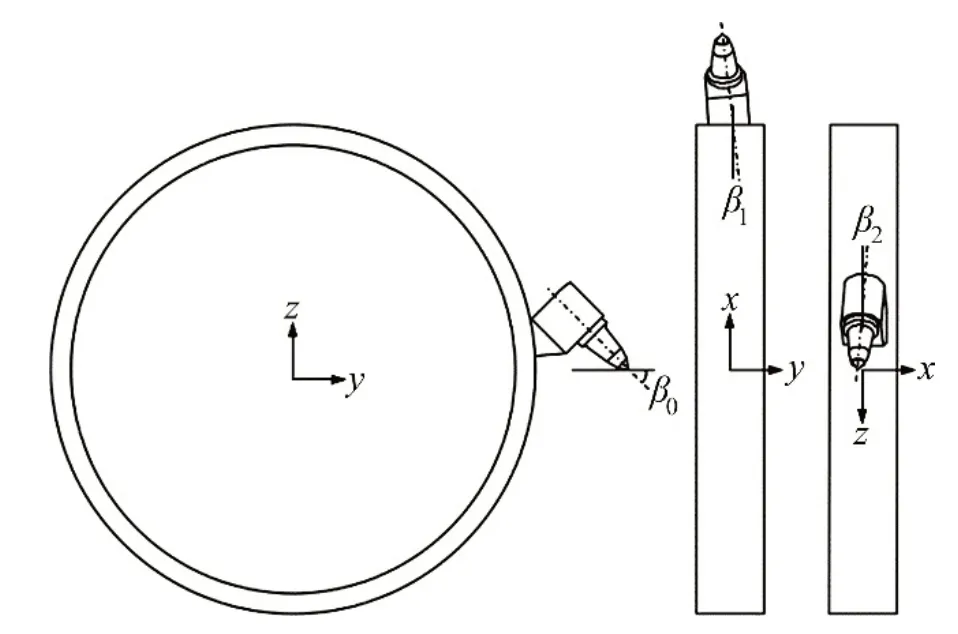
圖5 端盤截齒安裝角度Fig.5 Installation angles of transverse flange pick

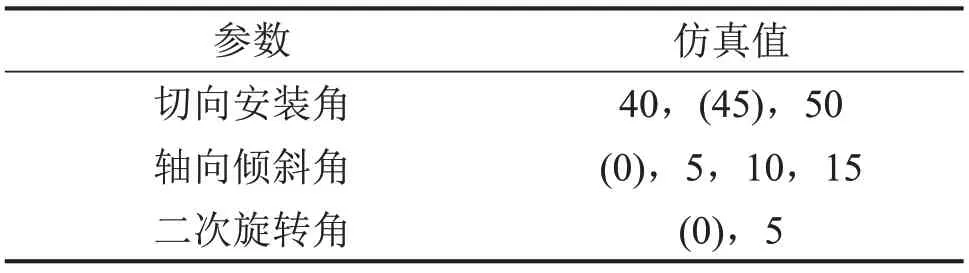
表2 截齒安裝角度Table 2 Installation angles of transverse flange pick(°)

2.2 有限元模型的建立

端盤截齒采用MT/T246—2006 采掘機械用標準，滾筒直徑為800 mm，截齒長為152 mm，合金頭直徑為18 mm，錐角為80°。塊狀硫化物礦體界面沿切削軌跡方向弧長為160 mm，寬度為 200 mm，厚度為100 mm，礦體本構模型調用自定義HJC 本構模型代碼模擬鎬形截齒旋轉破碎SMS 礦體的動態過程，主要材料參數如表3所示。

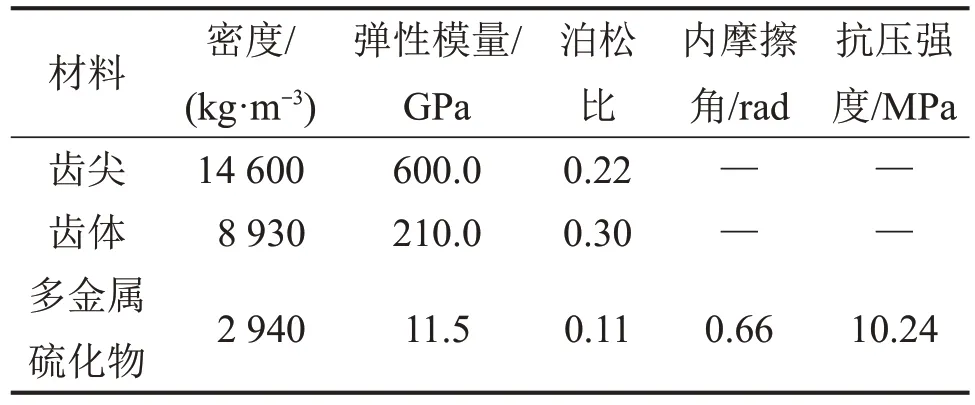
表3 截齒和海底塊狀硫化物材料屬性Table 3 Material properties of pick and SMS orebody

在仿真過程中，截割厚度固定為30 mm。為模擬圍壓環境，約束礦體的位移和旋轉自由度，并在截齒與礦體接觸的自由面上施加均布壓力載荷。根據塊狀硫化物礦床所處海底深度，取圍壓范圍為10～30 MPa。礦體單元設置類型為C3D8R，并且將截齒和礦體侵徹部分網格進行加密以提高計算精度。端盤截齒旋轉切削礦體有限元模型如圖6所示。

圖6 端盤截齒旋轉切削SMS有限元模型Fig.6 Finite element model of transverse flange pick rotary cutting SMS

2.3 載荷提取與處理

端盤截齒切削礦體載荷按照方向可分為：與切削軌跡相切的截割阻力；沿深度方向的進給阻力；與切削軌跡面垂直的側向力。端盤截齒旋轉切削載荷示意如圖7所示，截齒三向載荷可通過換算得到，換算公式如下：

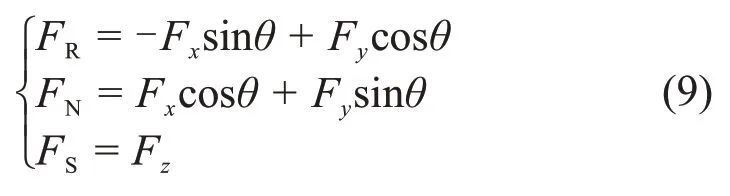
其中：FR為截割阻力；FN為進給阻力；FS為側向阻力。

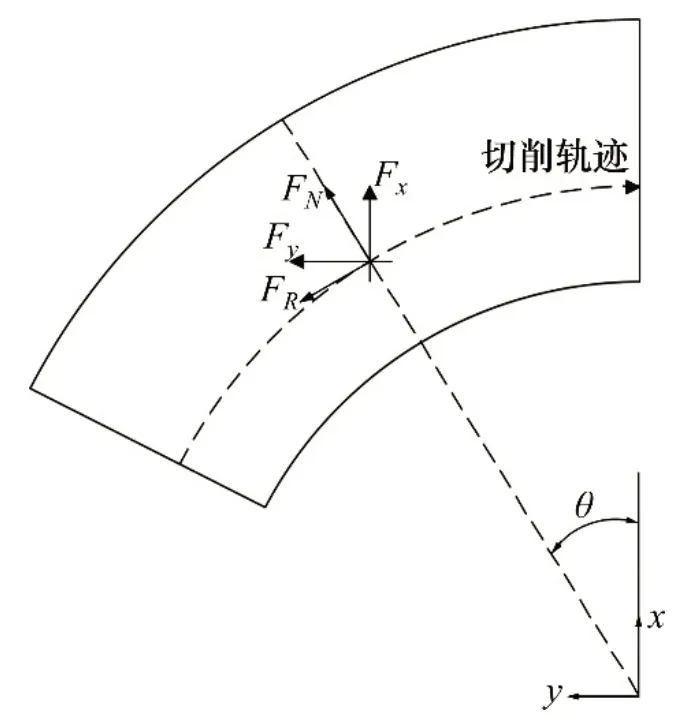
圖7 端盤截齒旋轉切削載荷分解示意圖Fig.7 Schmatic diagram of load decomposition of transverse flange pick

在端盤截齒切削礦體過程中，其載荷特性在空間上呈現為波動無常的隨機載荷，在工程作業中可能發生強烈震動，對截齒壽命產生極大影響，嚴重時可能發生崩齒狀況。研究表明，端盤截齒工作在封閉或半封閉狀態，工作條件惡劣，側向力波動將會直接影響截齒單側截割破碎效率，故引入載荷波動系數δ作為SMS 礦體切削效率的評價指標：

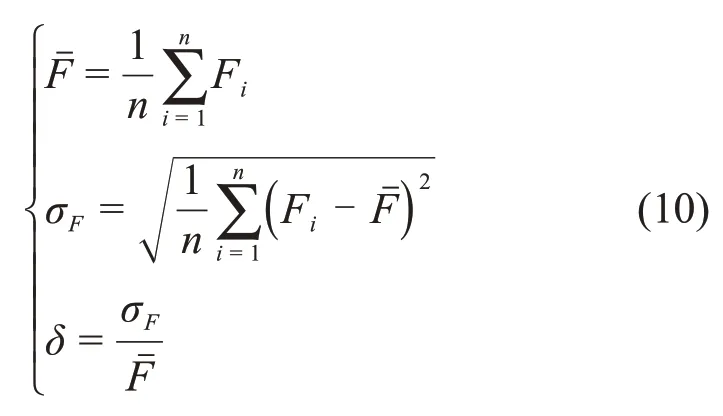
其中：為載荷均值；n為總的數據點數；Fi為第i個數據點處的載荷；σF為載荷標準差。

3 仿真結果及分析

3.1 圍壓對破碎性能的影響

端盤截齒在不同圍壓環境下破碎塊狀硫化物礦體時，其三向載荷和載荷波動如表4所示。在不同圍壓下，截齒三向阻力隨時間的變化如圖8所示。由表4和圖8可以得到：隨著圍壓增加，三向阻力增大，三向阻力波動系數明顯減小，這主要是由于高海水圍壓直接導致礦體的宏觀力學性能增強，抗拉及抗壓強度增大，裂紋難以產生，同時，裂紋擴展也受到高海水圍壓抑制，切屑更難以從基巖剝離；隨著海水圍壓增加，高壓海水不但會抑制截齒的振動，而且會使塊狀硫化物塑性發生變化，使得截齒破巖時被切屑所包裹，周圍的海水對累積在刀具前刀面的切屑有很大的壓力和粘著力，最終使截齒三向阻力增大，載荷波動性減小。

表4 不同圍壓下破碎性能統計Table 4 Crushing performance statistics of different confining pressures

3.2 切向安裝角對破碎性能的影響

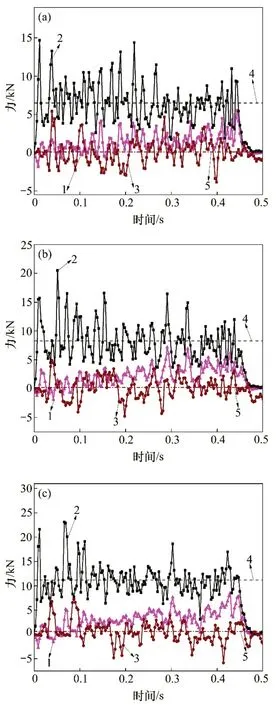
圖8 不同圍壓時端盤截齒三向阻力曲線Fig.8 Curves of three-direction resistance with time under different confining pressures

在20 MPa 圍壓下，端盤截齒以不同圓周切向安裝角進行硫化物礦體破碎時，其三向載荷和載荷波動情況如表5所示。在不同切向安裝角下，切削過程中三向阻力隨時間的變化見圖9。結合表5和圖9可以看出：隨著切向安裝角增大，截齒截割阻力FR均值呈現先減小后增大的趨勢，而截齒進給阻力FN和側向阻力FS變化不大，說明圓周切向安裝角主要影響截齒的截割阻力；當圓周切向安裝角β0=45°時，截齒截割力均值有極小值且存在較小的波動，易達到最高效率。這是因為切向安裝角越大，越不利于截齒截入礦體，切向安裝角越小，截齒后刀面與礦體的摩擦越嚴重；當切向安裝角取中值時，截齒垂直楔入巖石和橫向楔入巖石的力分配更加合理，這樣，不但使礦體楔入部分更容易破碎，而且使礦體更容易剝落。

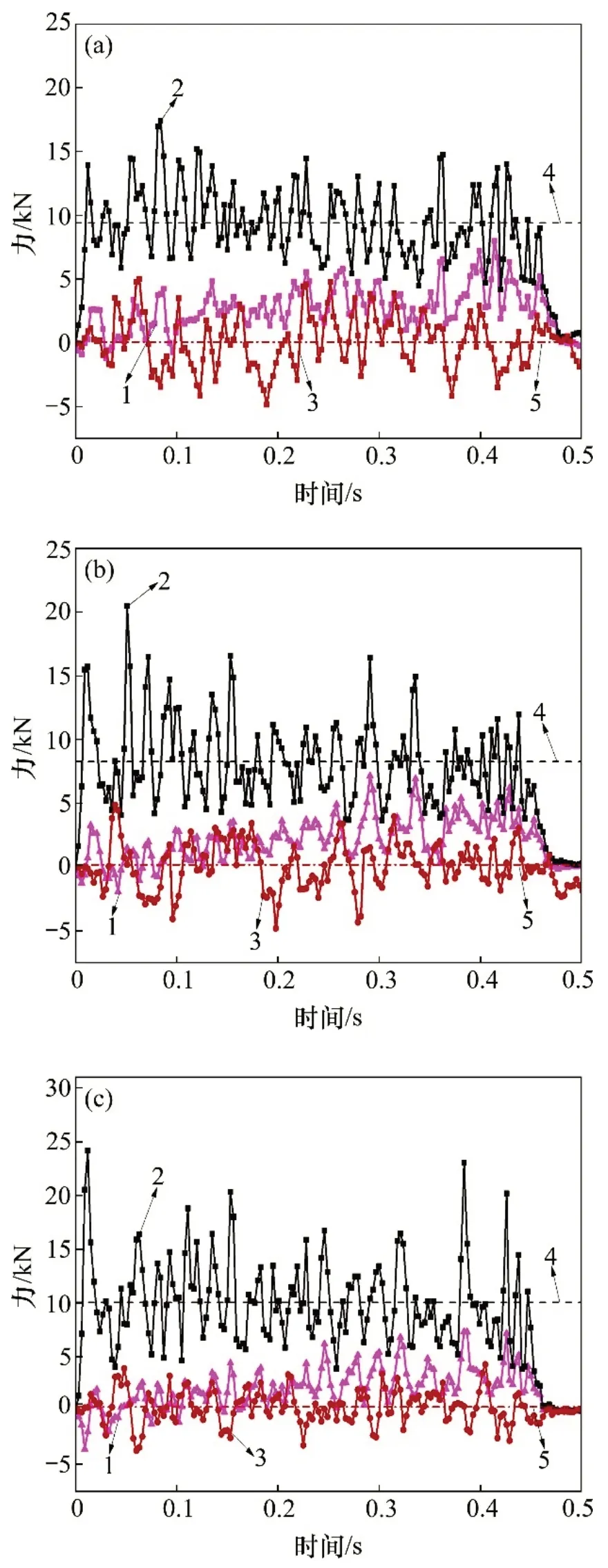
圖9 不同切向安裝角時端盤截齒三向阻力曲線Fig.9 Curves of three-direction resistance with time under different tangential installation angles

3.3 軸向傾斜角對破碎性能的影響

當圍壓為20 MPa 時，在不同軸向傾斜角下，端盤截齒三向載荷和載荷波動見表6。在不同軸向傾斜角下，切削過程中三向阻力隨時間的變化曲線見圖10。對比表5和表6、圖9和圖10 可以得到：當軸向傾斜角為0°時，側向力FS均值很小，基本沿z軸兩側波動；而當軸向傾斜角取5°～15°時，側向力FS波動傾向于沿z軸負向變化，截齒出現單側受力現象，說明截割時兩側煤巖不同時崩落，產生了側向力差值，并隨著軸向傾斜角的增大而更加明顯；當端盤截齒β1=10°時，截割阻力均值出現極小值，此時，礦壁剝落使截齒單側受力明顯，截割效率最高。

3.4 二次旋轉角對破碎性能的影響

二次旋轉角通常取0°或5°，當圍壓為20 MPa時，在不同端盤截齒二次旋轉角下，截齒三向載荷和載荷波動情況見圖10。在不同二次旋轉角下，切削過程中三向阻力隨時間的變化曲線見圖11。從表7和圖11 可以看出：隨著二次旋轉角增加，端盤截齒沿二次旋轉方向逐漸傾斜，側向力FS均值和峰值沿z軸負向增大明顯，說明在端盤截齒截割過程中，齒尖側礦石剝落更加容易，可以更好地形成截割壁面，有利于單側截割工況；而當二次旋轉角β1=5°時，截割力FR均值和峰值變化幅度較小且載荷波動較小，此時，端盤截齒截割效率較高。

表5 不同切向安裝角破碎性能統計量Table 5 Crushing performance statistics of different tangential installation angles

表6 不同軸向傾斜安裝角破碎性能統計量Table 6 Crushing performance statistics of different axial tilt angles

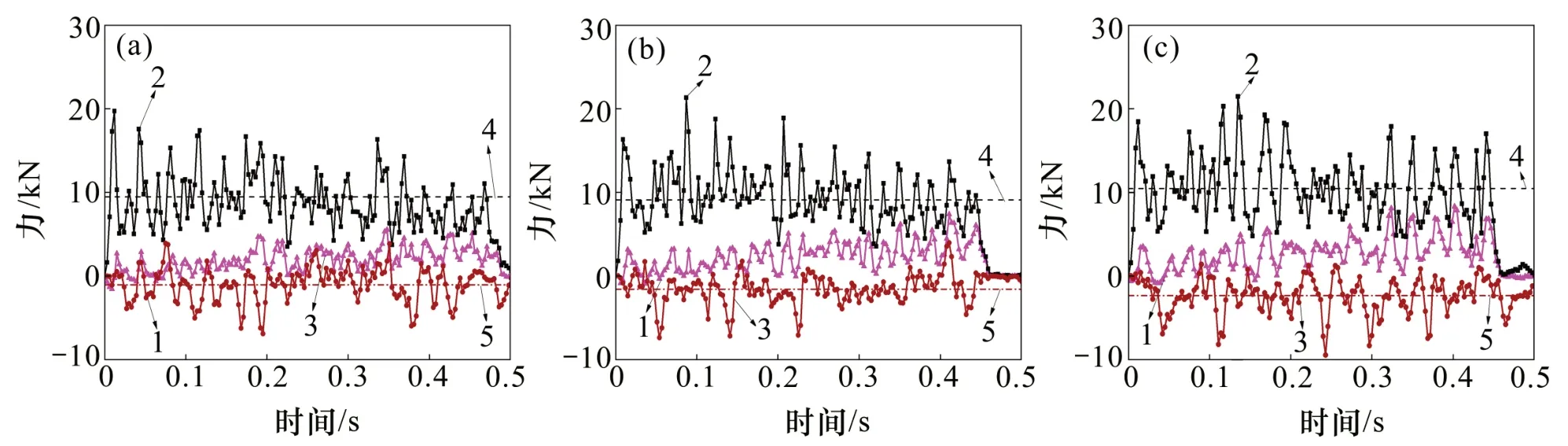
圖10 不同切向安裝角時端盤截齒三向阻力曲線Fig.10 Curves of three-direction resistance with time under different tangential installation angles

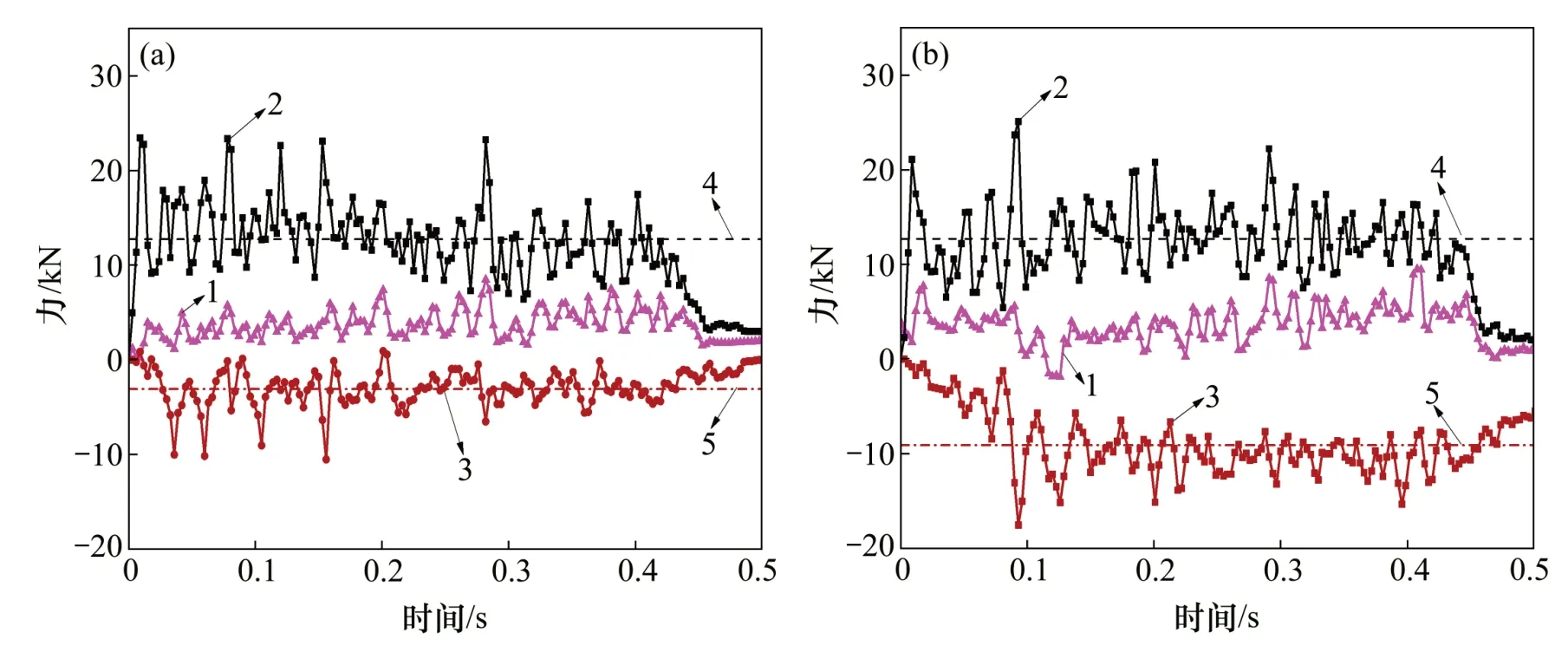
圖11 不同二次旋轉角時端盤截齒三向阻力曲線Fig.11 Curves of three-direction resistance with time under different secondary rotating angles

表7 不同二次旋轉角破碎性能統計量Table 7 Crushing performance statics of different secondary rotating angles

4 結論

1)借助VUMAT用戶材料子程序接口，自定義HJC多金屬硫化物本構模型代碼，并將本構模型嵌入ABAQUS/Explicit 分析模塊，通過將SMS 礦體樣品三軸壓縮實驗和單個單元下的數值仿真進行對比，驗證了VUMAT自定義HJC本構模型方法的可靠性。同時，與ANSYS/LS-DYNA 中內置的HJC本構模型數值仿真結果進行對比，說明了自定義HJC本構模型的優越性。

2)圍壓對于三向阻力有顯著影響，隨著圍壓增加，三向載荷增加，載荷波動減小。

3)側向力波動是造成截齒疲勞斷裂的主要原因，同時，軸向傾斜角和二次旋轉角對側向力的影響較大。當圓周切向安裝角β0=45°，軸向傾斜角β1=10°，二次旋轉角β2=5°時，截齒的截割效率較高，載荷波動較小。

4)端盤截齒安裝參數對SMS 礦體的切削破碎有較大的影響。在進行海底多金屬硫化物采掘頭設計時，不能忽視圓周切向安裝角、軸向傾斜角，二次旋轉角這3個重要的因素。本文的仿真模型充分利用了數值分析工具的優勢，在一定程度上定量分析了圓周切向安裝角、軸向傾斜角和二次旋轉角對截齒切削破碎阻力的影響，可為端盤截齒結構改良和采掘頭參數優化提供參考。