基于數據挖掘的寬厚板板凸度控制

曹建國，江軍，趙秋芳，何安瑞，李存福，孫旭東

(1.北京科技大學機械工程學院，北京，100083；2.北京科技大學國家板帶生產先進裝備工程技術研究中心，北京，100083；3.北京科技大學人工智能研究院，北京，100083；4.北華航天工業(yè)學院機電工程學院，河北廊坊，065000；5.江蘇金恒信息科技有限公司，江蘇南京，210045；6.南京鋼鐵股份有限公司，江蘇南京，210035)

隨著制造業(yè)對高強管線鋼、壓力容器板、船板等需求的提升，人們對寬厚板板形質量的要求日趨嚴苛，寬厚板軋機板形控制已成為寬厚板質量控制的關鍵技術之一。特別是對于火箭衛(wèi)星外殼、船艦、海上平臺、核能設備等鋼板質量大的寬厚板產品，必須依靠5 m及以上強力寬厚板軋機才能軋制[1]，多為單機架多道次的可逆軋制過程，頻繁的規(guī)格變化提升了寬厚板軋機板形控制的難度。寬厚板軋制過程中板形影響因素繁雜，因而難以進行機理建模，難以穩(wěn)定實現寬厚板板凸度高精度有效控制。同時，由于缺乏適當的處理技術和方法，寬厚板生產過程積累的大量重要軋制過程數據未能得到充分的利用。數據挖掘作為20世紀末興起的數據智能分析技術，能夠從海量數據中自動分析潛在有用的知識，隨著數據挖掘技術和數據挖掘產品的普及，各鋼鐵企業(yè)均開展了數據挖掘的研究，希望將數據挖掘應用于鋼鐵企業(yè)質量控制、質量改進等方面。國內外學者在中厚板軋制過程數值模擬[2?3]、板形控制策略[4?5]和數學模型[6?7]等方面取得了豐富成果。近年來，在寬厚板板形控制研究中也取得了積極進展：PRINZ等[8]針對寬厚板軋制過程中的橫向不對稱問題，提出一種基于寬厚板位置評估的前饋控制策略，在工業(yè)應用中有效提高了寬厚板平面形狀的控制精度；穆志純等[9]采用知識發(fā)現和數據挖掘的方法建立了一種將知識模型和數學模型相結合的軋制負荷分配模型，通過該模型生成的規(guī)程進行軋制可以提高寬厚板板形質量；李揚等[10]以帶鋼成品寬度質量分析為目標，利用關聯規(guī)則挖掘得到帶鋼寬度質量缺陷與控制狀態(tài)的對應關系，結合因子分析和故障邏輯分析方法進行帶鋼質量的綜合評估。國內某寬厚板CVC plus 大型骨干軋機具有工作輥竄輥、工作輥彎輥和CVC plus 輥形等先進的板形控制手段，是世界上軋制扭矩最大和我國軋制壓力最大的寬厚板軋機之一，實際生產中存在板凸度偏大且難以控制的問題。本文作者結合數據挖掘以及寬厚板生產特點，基于歷史數據建立高精度的板凸度預測模型，在離散的狀態(tài)空間上對基于主成分分析方法提取的關鍵控制變量與預測板凸度狀態(tài)間進行關聯規(guī)則挖掘，結合控制變量影響力評估實現不同板凸度質量狀態(tài)下關鍵控制變量的快速定位以及對板凸度的有效控制，避免機理建模對問題分析帶來的困難，實現對歷史數據中蘊含信息的充分利用，為寬厚板板凸度控制研究提供參考。

1 現場數據采集與分析

國內某寬厚板CVC plus 大型骨干工業(yè)軋機采用單機架多道次的可逆軋制方式，能夠進行最小厚度為8 mm、最大寬度為4 850 mm以及厚度超過100 mm的高品質寬厚板的軋制。現場測量210 塊Q345 鋼寬厚板板凸度，測量結果如圖1所示。在實際生產過程中，寬厚板板凸度一般要求控制為0.12 mm 左右，0～0.15 mm 屬于可接受范圍，板凸度超過0.15 mm 時表示凸度控制應引起足夠的重視，板凸度超過0.2 mm 時判定為不合格。在現場采集數據中，板凸度大于0.2 mm的寬厚板占比為6.2%，板凸度為0.15～0.20 mm的寬厚板占比為35.7%，其板凸度質量控制存在較大的提升空間。同時，由于其產品規(guī)格多，不同規(guī)格寬厚板的軋制工藝存在差異，包含有11道次、13道次、15道次和17道次等的可逆軋制過程，軋制過程工藝參數較為繁雜，為寬厚板板凸度質量控制研究帶來了較大阻礙。

圖1 Q345鋼板板凸度分布Fig.1 Distribution of Q345 steel plate crown

2 寬厚板板凸度預測模型的建立

為及時采取有效措施避免板凸度質量問題的發(fā)生，寬厚板板凸度控制需要通過對歷史生產數據分析以實現待軋制寬厚板板凸度質量的預先判定，因此有必要建立高精度的寬厚板板凸度預測模型進行研究。雖然神經網絡等人工智能算法具有很強的非線性和自學習能力，但這類單分類器對訓練樣本的依賴程度過高并且容易出現過擬合的現象[11]，為提高板凸度預測的準確度和穩(wěn)定性，采用隨機森林集成方法建立板凸度預測模型。

2.1 選取預測因子

由于寬厚板軋制主要在精軋階段進行板凸度控制，因此選取精軋10道次穩(wěn)定軋制階段的軋制過程數據建立預測數據集，并進行變量重命名以區(qū)分各道次軋制過程控制變量，如dthick_en_1代表第1道次軋件入口厚度。根據現場經驗，選取包含各道次出口厚度、彎輥力和竄輥量等在內的83個控制變量作為備選解釋變量。為減小解釋變量維度過高對預測模型計算效率的影響，對解釋變量作進一步篩選。依據均方誤差對解釋變量的重要性進行排序，隨機改變解釋變量取值并生成對應的隨機森林模型，計算袋外數據(out of bag,OOB)誤差，OOB 誤差變化越大則解釋變量的重要性越高[12]。同時，對數據集進行十折交叉驗證(10-fold cross-validation)，得到OOB 誤差隨變量數的變化關系，如圖2所示。由圖2可以得出：當變量數為42個時，OOB 誤差最小，因此，選取重要性排序在前42 位的變量作為隨機森林預測模型的預測因子。

圖2 OOB誤差隨變量數變化曲線Fig.2 OOB error curve with variable number

2.2 參數選擇和優(yōu)化

隨機森林模型中需要設置隨機森林決策樹數ntree和決策樹每個節(jié)點處隨機選取的候選特征數mtry這2個主要參數，ntree一般不少于100棵，默認值為500 棵，mtry一般取為預測因子數的1/3[13]。為避免單純依靠經驗選取模型參數可能帶來的預測偏差，采用遍歷的方法確定隨機森林模型參數ntree和mtry最佳值。分別計算ntree在和mtry所有取值情況下的袋外誤差，袋外誤差最小時的參數值就是ntree和mtry的最佳取值。將mtry的取值范圍設定為12～18個，ntree可選擇的取值設定為500，1 000，1 500和2 000 棵，袋外誤差隨mtry和ntree的變化如圖3所示。由圖3可知：mtry和ntree的最佳取值分別為16個和1 000個。

210組數據中隨機選擇170組數據組成訓練集，其余40 組數據組成測試集，采用自助抽樣法(bootstrap)隨機產生1 500個子訓練集并生成對應未剪枝的決策樹。從43個特征中隨機抽取16個特征作為節(jié)點的分裂特征集，在每個節(jié)點處以Gini 指數為標準從16個特征中選擇最佳的分裂方式，分裂過程不進行剪枝使每棵決策樹最大限度地生長。取1 000棵決策樹輸出結果的平均值作為最終的板凸度預測結果。隨機森林預測模型計算流程如圖4所示。

圖3 袋外誤差隨mtry和ntree變化曲線Fig.3 OOB error variation curve with mtry and ntree

2.3 建立預測模型

應用經過訓練的RF 模型進行測試集板凸度預測，預測結果如圖5所示。依據預測結果分別計算模型平均相對誤差絕對值MMRE、均方根誤差RRMSE和確定性系數R2，分別統計訓練階段和測試階段模型的性能指標，以對模型的可靠性和精度進行評價，結果如表1所示。由表1可知：RF模型精度較高，測試期預測相對誤差未超過訓練期預測相對誤差，泛化性較好；均方根誤差反映誤差波動程度，RF 模型2個階段預測均方根誤差均較小，預測值比較穩(wěn)定；確定性系數反映預測準確性，測試期與訓練期的確定性系數均接近1，預測數據基本可以擬合實際數值，因此預測模型能合理準確地對板凸度進行預測。從圖5 可以看出：RF 預測結果與實際值較為吻合。綜上可知，RF 預測效果理想，表現出良好的泛化性能，能夠滿足寬厚板板凸度預測要求。

3 基于關聯規(guī)則挖掘的寬厚板板凸度質量分析

關聯規(guī)則挖掘是數據挖掘中的一種重要技術手段，對于由隨機森林模型板凸度預測結果和對應軋制過程工藝參數的1 208 組數據構成的數據庫，應用關聯規(guī)則中的Apriori 經典算法分析找出板凸度與控制狀態(tài)之間的強關聯關系，得到軋制過程工藝參數對于板凸度的影響規(guī)律，有助于快速定位軋制過程中造成板凸度偏大的關鍵工藝參數。

3.1 主成分分析法數據降維

由于寬厚板多道次可逆軋制過程中影響板凸度的因素復雜多樣，各因素相互作用共同決定了最終的板凸度，但各因素重要性存在一定差異，同時對板凸度的影響規(guī)律也不完全相同，在進行板凸度分析時要抓住關鍵過程控制變量，忽略次要因素對板凸度的影響。因此，在進行關聯規(guī)則挖掘前有必要進行數據降維工作，同時對于減少冗余規(guī)則數具有重要作用。

圖4 隨機森林模型板凸度預測計算流程Fig.4 Calculation process of plate crown using random forest prediction model

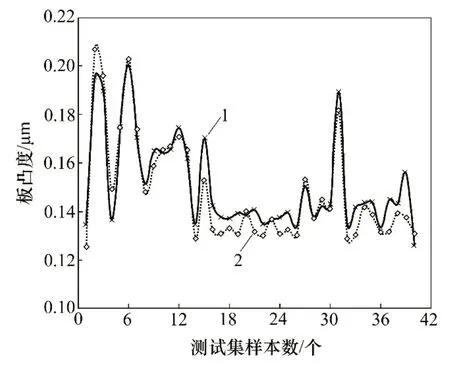
圖5 RF模型預測結果Fig.5 RF model prediction results

表1 訓練期和測試期RF模型預測性能Table 1 Prediction performances of RF model in training and testing periods

主成分分析是最常用的線性降維方法，通過某種線性投影將高維的數據映射到低維的空間中表示，并期望在所投影的維度上數據的方差最大，以使用較少的數據維度，同時能夠將數據包含信息的損失降為最低[14]。

對于樣本矩陣x：

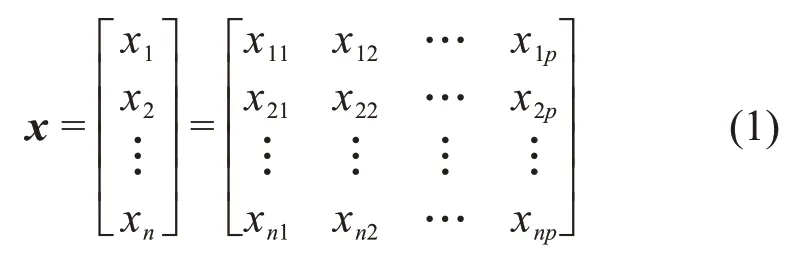
式中：p=1,2,…,83;n=1,2,…,1 208。

對式(1)進行Z標準化處理，得到標準化后的向量x*為

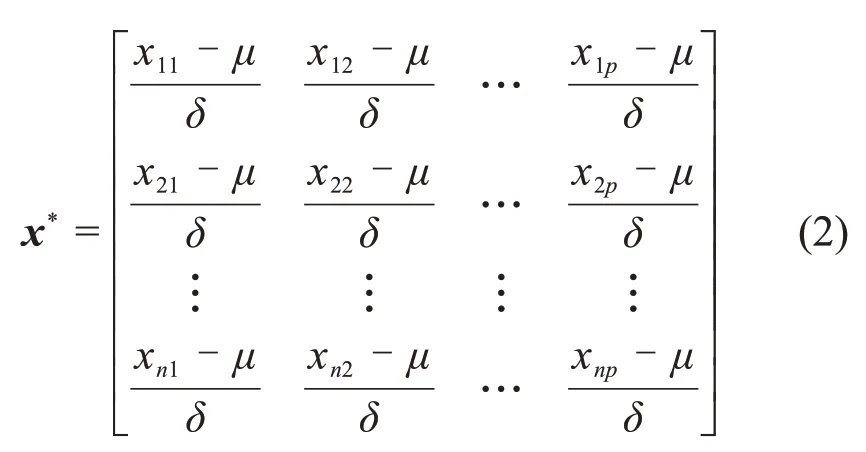
計算x*協方差矩陣的特征值λ1,λ2,…,λp和特征向量ω1,ω2,…,ωp，則主成分的貢獻率P表示為

提取特征值大于1的13個主成分，該13個主成分的累積貢獻率為90.10%，可以用于代表全部數據信息。由于主成分因子沒有明確的實際含義，不能作為實際的控制變量，但主成分中影響顯著的變量可以代表主成分包含的主要信息，因此通過主成分載荷矩陣進行關鍵變量的選取[15]。主成分載荷矩陣反映主成分與原始變量間的相互關聯程度，原始變量xj在第p個主成分zi上的載荷lij可以表示為

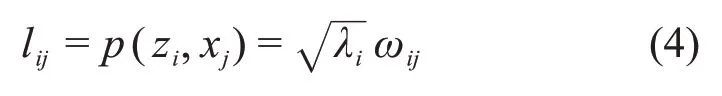
式中：i,j=1,2,…,83；λi為特征值，ωij為特征向量ωi的第j個分量。

選用每個主成分中影響最為顯著的變量作為關鍵控制變量，以此來降低產生規(guī)則的規(guī)模，由于第一主成分包含的信息最多，因此，從第一主成分中選取3個關鍵控制變量。篩選出的關鍵控制變量如下：dthick_ex_1，dthick_ex_2，dthick_ex_3和dthick_ex_4分別為第1道次、第2道次、第3道次和第4道次出口厚度；Swr_shift_1，Swr_shift_6和Swr_shift_10分別為第1道次、第6道次和第10道次竄輥量；Ttemp_en_2，Ttemp_en_3和Ttemp_en_4分別為第2道次、第3道次和第4道次入口溫度；Ttemp_ex_10為第10道次出口溫度；Qwr_bend_5，Qwr_bend_6和Qwr_bend_9分別為第5道次、第6道次和第9道次彎輥量；froll_force_10為第10道次軋制力。

關鍵控制變量的影響力w指的是關鍵控制變量對于最終寬厚板板凸度的影響權重，在數值上等于控制變量對主成分因子具有最顯著載荷l的絕對值與該主成分的貢獻率P的乘積，具體計算公式為

式中：p=1,2,…,83;n=1,2,…,1 208。

下面進行關鍵控制變量影響力的計算，并將計算結果進行量綱一處理，按照從大到小的順序進行排序，得到關鍵控制變量的權值向量表，如表2所示。

3.2 數值型屬性的離散化

Apriori 算法要求數據集中的數據類型必須為離散型，在應用Apriori 算法進行關聯規(guī)則挖掘前需進行數據的離散化操作[16]。進行目標變量(關聯規(guī)則后件)離散化操作時，根據實際生產經驗可知：寬厚板板凸度一般會控制為0.15 mm左右，板凸度超過0.2 mm時判定為不合格。根據這一實際情況，本文將板凸度劃分為A1，B1和C1這3個等級，如表3所示。通過目標變量的離散化操作賦予數據集類信息。

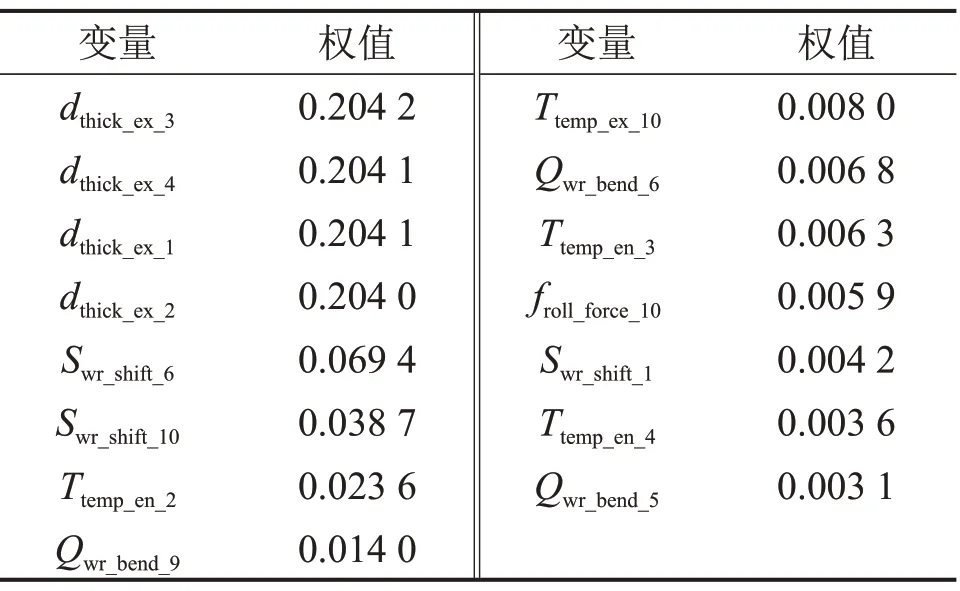
表2 關鍵控制變量權值Table 2 Weight of key control variables

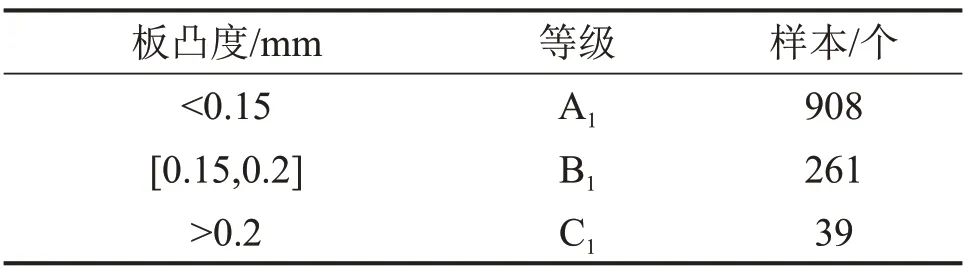
表3 板凸度離散化結果Table 3 Discrete results of plate crown

采用聚類分析進行關聯規(guī)則前件即控制變量數值型屬性的離散化，聚類分析考慮屬性的取值分布和數據點的相鄰性，可以得到較理想的數據離散化結果[17]。采用Matlab編程實現K?means聚類算法進行數據離散化操作，將每個屬性劃分為8個區(qū)間(簇)，隨機選出8個數據項作為各簇的初始中心，分別計算剩余的數據項與各個簇中心的距離，將其歸入距離最短的簇中并重新計算8個簇的中心。重復進行上述過程，直至平方誤差準則函數E收斂。

式中：E為數據集中所有數據項的平方誤差和；q為數據項；mi為簇Ci的均值；k為簇的數目。

為使數據規(guī)整以便于進行數據挖掘，進一步將離散區(qū)間映射成連續(xù)的字母標識，如Swr_shift_1的離散化結果如表4所示。

3.3 基于Apriori算法的關聯規(guī)則挖掘

設項集Xt={i1,i2,…,ip}(p=1,2,…,15)，Y={b}，其中i1,i2,…,ip分別代表dthick_ex_3，dthick_ex_4，dthick_ex_1等15個關鍵控制變量1個值域內的子區(qū)間，b代表板凸度取值的1個子區(qū)間，包含A1，B1和C1這3個等級，需要尋找出形如X?Y的關聯規(guī)則[18]。由于寬厚板凸度為B1和C1等級出現次數較少，這些少數狀態(tài)是進行板凸度分析需要重點研究的內容，因此，在進行關聯規(guī)則分析時需設置1個較低的支持度，設定最小支持度為1%，最小置信度為50%。由于板凸度為A1的控制狀態(tài)出現次數最多，在產生對應的關聯規(guī)則時將最小置信度設置為80%以保證關聯規(guī)則的有效性。篩選目標厚度為20 mm 且目標寬度為3 910 mm、目標厚度為25 mm 且目標寬度為3 150 mm和目標厚度為35.5 mm且目標寬度為4 240 mm這3種典型規(guī)格樣本的關聯規(guī)則，如表5所示。

4 基于關聯規(guī)則的關鍵工藝參數調整策略及仿真分析

4.1 基于關聯規(guī)則的關鍵工藝參數調整策略

在數據挖掘數據集中查找滿足板凸度等級為A1時對應關聯規(guī)則的樣本，從中選取寬厚板凸度最小的樣本組成標準樣本集，作為關鍵工藝參數調整的參照標準，如表6所示。當來料情況一定時，規(guī)格相同的寬厚板軋制過程各板形調控手段的使用會發(fā)生變化，現場技術人員會根據實際軋制條件做出調整，最終寬厚板板凸度也會存在差異。將板凸度等級為B1和C1與板凸度等級為A1對應的關聯規(guī)則中存在的相同控制變量作為需要調整的關鍵控制變量，將關鍵控制變量的差異性作為制定調控策略的依據，并參照標準樣本集關鍵控制變量設定值進行相應調整，以實現對板凸度的控制。通過適當調整關鍵控制變量實現良好的板凸度控制，并以典型厚度規(guī)格樣本與所選取標準樣本關聯規(guī)則對比分析結果為依據，制定關鍵工藝參數調整策略。

表4 Swr_shift_1離散化結果Table 4 Discrete results of Swr_shift_1

表5 3種典型規(guī)格下樣本的關聯規(guī)則Table 5 Association rules of samples with three typical specifications

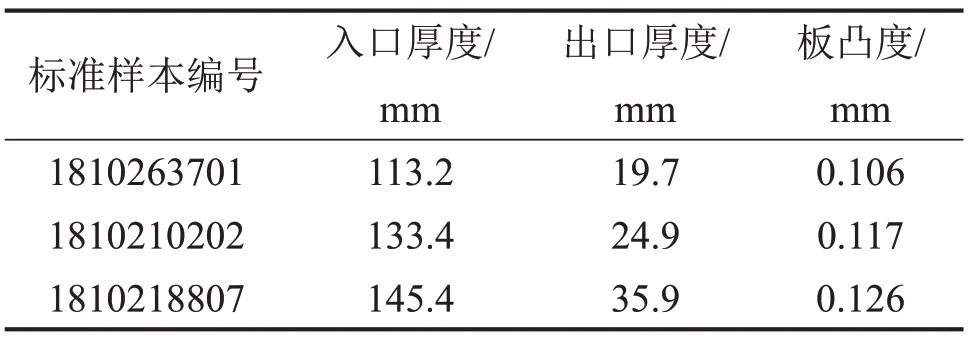
表6 標準樣本集Table 6 Standard sample set

所建立的關鍵工藝參數調整策略如下：

1)在進行目標厚度為20 mm、目標寬度為3 910 mm的寬厚板軋制時，在現階段軋制工藝條件下，應減小精軋第5道次的彎輥力，將其保持在1 914～2 137 kN，應在第6道次進行正竄輥，竄輥量設定為50.5～69.7 mm，此時精軋第6道次的輥縫由負凸度變?yōu)檎苟龋瑴p小了第6道次的板凸度。

2)在進行目標厚度為25 mm、目標寬度為3 150 mm的寬厚板軋制時，在現階段軋制工藝條件下，應減小精軋第6道次和第10道次的竄輥量，將第6道次的竄輥量控制為8～29 mm，第10道次的竄輥量控制為6.6～30.7 mm。

3)在進行目標厚度為35.5 mm、目標寬度為4 240 mm的寬厚板軋制時，在現階段軋制工藝條件下，應減小精軋第5道次的彎輥力，將其控制為2 817～3 108 kN，同時減小精軋第10道次的負竄輥量，將其控制在?55.7～?33.8 mm，在精軋最后一個道次通過CVC plus 軋機的工作輥負竄輥進一步減小寬厚板的板凸度。

4.2 基于關聯規(guī)則的關鍵工藝參數調整策略有限元分析

運用大型通用商用有限元軟件ANSYS 建立寬厚板輥件一體化三維彈塑性有限元耦合分析模型[19?21]，通過輥系彈性變形模型獲取有載輥縫形狀并加載到軋件彈塑性變形模型中進行寬厚板關鍵工藝參數調整策略的仿真計算，用于驗證方法的可行性。在建立輥系彈性變形模型時，由于軋輥輥身的對稱性以及上、下軋輥的反對稱性并考慮計算資源的限制，建立輥系的1/4模型，對工作輥與支持輥輥間接觸區(qū)域以及工作輥與軋件間接觸區(qū)域選用Solid95 二十節(jié)點六面體高階等參單元，其余部分選用Solid45 八節(jié)點六面體等參單元。在工作輥和支持輥以及工作輥與軋件之間可能發(fā)生接觸的區(qū)域附加接觸單元，對于工作輥和支持輥間的面?面接觸，將支持輥表面設置為目標面，工作輥表面設置為接觸面；對于工作輥和軋件間的面?面接觸，將工作輥表面設置為目標面，軋件表面設置為接觸面，目標面使用的單元號為Target170，接觸面使用的單元號為Contact173[19]。在建立軋件彈塑性變形模型時，取輥系和軋件的1/4 進行建模，軋輥采用剛性材料模型，軋件采用雙線性等向強化彈塑性材料模型，采用Solid164六面體實體單元劃分網格[20]，輥系采用間接耦合。建立的有限元耦合模型中軋輥的綜合輥形包含原始磨削輥形、磨損輥形和熱輥形。建模參數如表7所示，建立的有限元模型如圖6所示，其中軋件模型厚度方向網格劃分為10層。

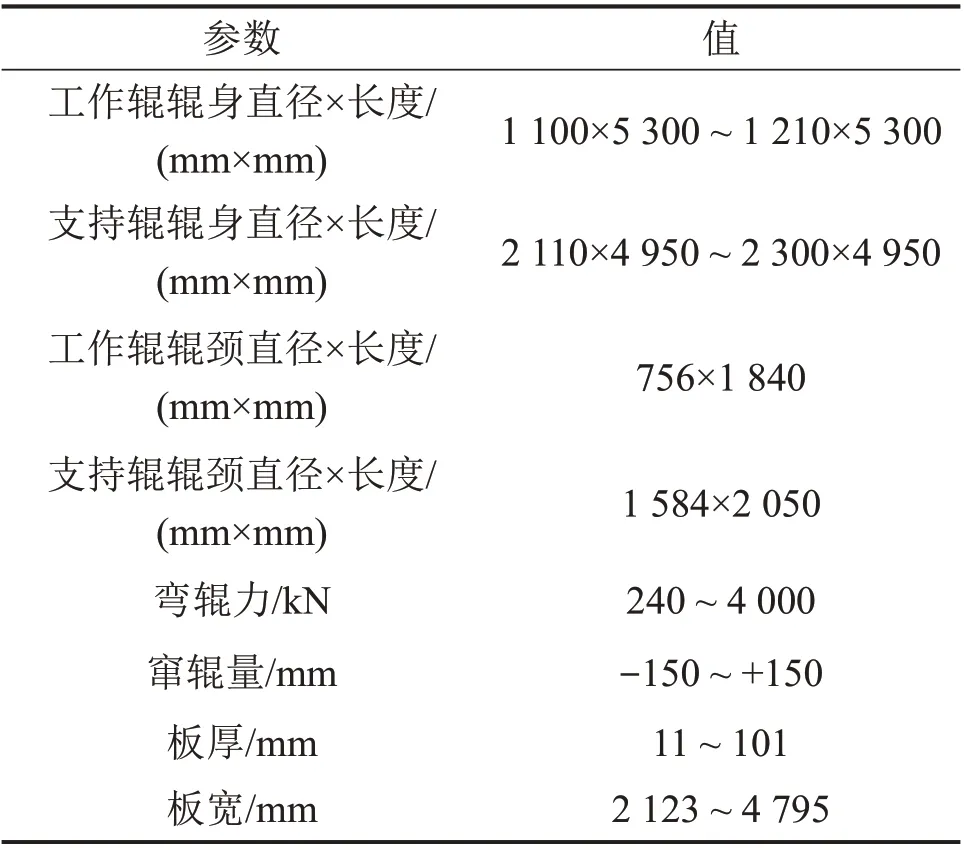
表7 有限元模型建模參數Table 7 Parameters of finite element model

選取精軋階段軋制工藝參數對應的3個工況進行初始條件設置，如表8所示。精軋板入口厚度分別為112.961，145.240和137.420 mm，板寬度分別為4 640.53，3 934.74和3 763.26 mm。依據有限元分析結果計算得到的板凸度分別為0.175，0.130和0.156 mm，實際測得的板凸度分別為0.163，0.120和0.148 mm，相對誤差為7.4%，8.3%和5.4%，有限元模型計算精度滿足工程要求。

圖6 三維彈塑性有限元耦合模型Fig.6 Three-dimensional elasto-plastic coupled finite element model

表8 仿真工況Table 8 Simulation conditions

分別選取編號為1810263705，1810195834和1810263208的樣本作為測試樣本，應用有限元耦合模型進行精軋10道次軋制過程的仿真計算，各個樣本的板凸度預測結果以及仿真計算結果如表9所示。由表9 可以看出：3個測試樣本的板凸度都在0.15 mm以內，板凸度得到了良好控制，說明本文提出的關鍵工藝參數調整策略對于進行板凸度控制是有效的，可為開展板凸度控制工業(yè)實驗提供參考。

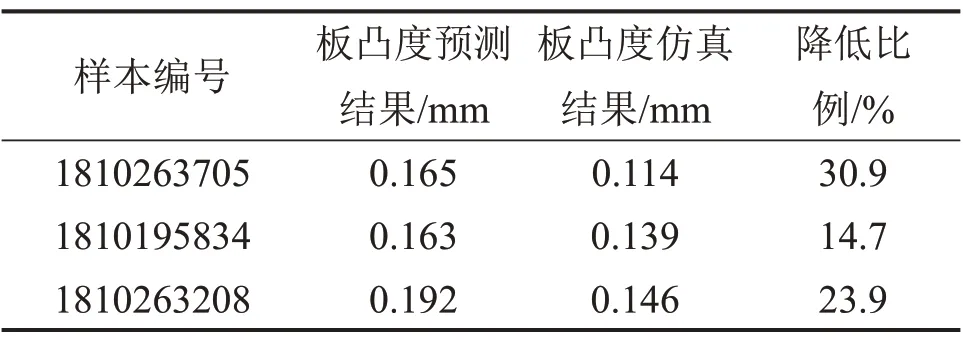
表9 板凸度仿真計算結果Table 9 Simulation results of plate crown

5 結論

1)應用隨機森林集成方法建立了寬厚板板凸度預測模型，模型預測結果的平均相對誤差絕對值、均方根誤差和確定性系數分別為0.038，0.046和0.850，表現出良好的泛化性能，能夠實現高精度的寬厚板板凸度預測。

2)通過主成分分析方法將數據集由83 維降至15 維，采用聚類分析方法進行數值型屬性的離散化操作，通過關聯規(guī)則挖掘實現對不同板凸度控制狀態(tài)下軋制過程關鍵控制變量的快速定位，并應用于3 種典型規(guī)格寬厚板關鍵工藝參數調控策略。

3)建立了三維彈塑性有限元耦合模型，對3種典型規(guī)格工藝參數調控策略進行了仿真分析，板凸度分別下降了30.9%，14.7%和23.9%，說明基于關聯規(guī)則的關鍵工藝參數調整策略可較好地控制板凸度，為開展基于數據挖掘的板凸度控制工業(yè)實驗提供了參考依據。